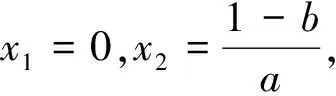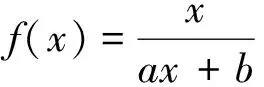思维盲点在哪儿？*

江苏省海门市海门中学 (226100) 樊陈卫

很多数学问题在解题过程中存在一些容易被忽视的环节或要点，比如不等式两边同乘于一个参数或未知数时，会忽视这个参数或未知数是正是负还是零的讨论；集合问题中往往忽视空集这一特殊情况；运用点斜式或斜截式直线方程时可能会忽略斜率不存在的情况；运用等比数列求和公式时有可能忘记了对公比是否为1的讨论.对于诸如此类存在思维盲点的问题，解题时要时刻保持警惕.教师可以在教学中充分挖掘这些问题的价值，有意识引导学生在解题时不断反思，捕捉解题思维过程中的盲点，培养思维的严密性和深刻性.笔者以一个分式函数问题为例加以剖析：

这道题看似不难解决，只要把问题进行简单转化和变形，根据方程f(x)=x有唯一解这一条件，容易求得a，b的值.可从学生解答的实际情况看事实并非如此.笔者有意把学生的普遍思路在课堂上呈现出来，师生探寻整个解题过程中的思维盲点.

图1

图2

针对思路1，笔者在课堂上对学生提出建议：回顾对于上述过程中每一步，能否确认没有遗漏任何尚未考虑的情形？

经过充分的观察与思考后，有学生发现了盲点

图3

到这里，大家以为可以大功告成时，笔者再次提醒：其它步骤中能确认没有遗漏任何情形了吗？

……

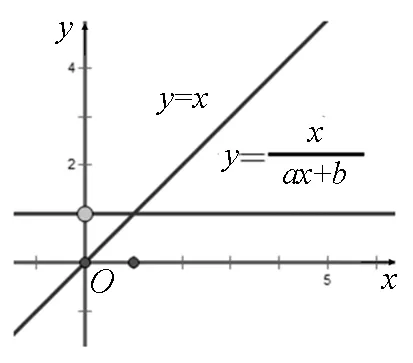
图4

盲点2——第二步ax2+(b-1)x=0有唯一解，故Δ=(b-1)2=0，忽视了二次项系数是否为零；故应补充a≠0的条件；盲点3——对于Δ=(b-1)2≠0时，若方程的非零根恰为方程ax+b=0的根，即为f(x)=x的增根，则方程f(x)=x仍有唯一解.分析了上述思维盲点，解题过程可以整理为如下：

2.当a≠0时，f(x)=x即为