考虑旅客需求的停站方案与列车运行图一体化模型与算法
2019-03-07刘璐孟令云李新毅刘岗
刘璐,孟令云,李新毅,刘岗
考虑旅客需求的停站方案与列车运行图一体化模型与算法
刘璐1,孟令云1,李新毅1,刘岗2
(1. 北京交通大学 交通运输学院,北京 100044;2. 天津南环铁路维修有限责任公司,天津 300381)
考虑高速铁路旅客出行的时空敏感性较高的特点,将旅客运输状态引入运输时空网络,构建三维的时间-空间-状态网络,提出基于旅客需求的停站方案与列车运行图综合优化0-1 整数规划模型,实现旅客分配、停站方案与列车运行图编制的一体化。设计拉格朗日松弛求解算法,将复杂的列车间强耦合问题分解为单列车的最短路径子问题集合,从而降低模型求解难度。以京沪高铁北京南-曲阜东区段为背景进行验证和分析,结果表明模型不仅实现了较低的运营成本,还能够有效满足旅客需求,实现客流分配、停站方案与列车运行图编制的有机联动。
铁路运输;列车运行图编制;拉格朗日松弛算法;综合优化;时空状态网络;旅客需求
列车运行图是铁路行车组织的基础,编制和优化运行图是铁路运输组织领域的经典问题。高速铁路的不断发展和社会生活水平的不断提高,旅客对时空的敏感性需求以及对铁路系统服务水平的要求不断增加,铁路部门需要通过考虑旅客需求来提高旅客服务水平,以提升在各种交通方式竞争下行业竞争力。此时考虑旅客需求的列车运行图编制显得尤为重要。大多数学者从铁路运营的角度出发,以铁路效益最大[1−3]、列车总旅行时间最小[4]、列车运行图的均衡性[4]等为目标,对列车开行方案或列车运行图进行独立优化,少量学者从旅客的角度,考虑旅客的时变需求、拥挤状态[5]、时间敏感度[3]等因素,以旅客总等待时间最小化[5]、旅客总旅行时间最小化[6]、旅客满意度最大化[3]等为目标函数,对列车运行图进行优化。少量学者对开行方案和列车运行图进行综合优化,周文梁等[7−9]结合基于旅客弹性需求的列车开行方案优化和定序优化的列车运行图优化,将列车开行方案和列车运行图作为整体构建双层规划模型,进行综合优化。既有考虑旅客需求的研究,大多将开行方案与列车运行图的优化进行割裂考虑,采取分阶段或独立优化的方法,容易造成优化目标和约束的不协调等问题。考虑综合优化的复杂性,本文考虑旅客需求的停站方案与列车运行图一体化优化问题。基于Mahmoudi 等[10]提出的VRPPDTW(Vehicle Routing Problems With Pickup And Delivery With Time Windows)问题,将旅客运输状态引入时空网络,构建三维的时间−空间−状态网络,实现旅客分配、停站方案与列车运行图编制的综合优化。设计拉格朗日松弛求解算法,将复杂的列车间强耦合问题分解为单列车的最短路径子问题集合,从而降低模型求解难度。最后以京沪高铁北京南−曲阜东下行的列车运行图编制为例进行案例分析。
1 运输时空状态网络
1.1 运输时空网络的构建
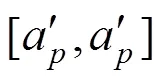
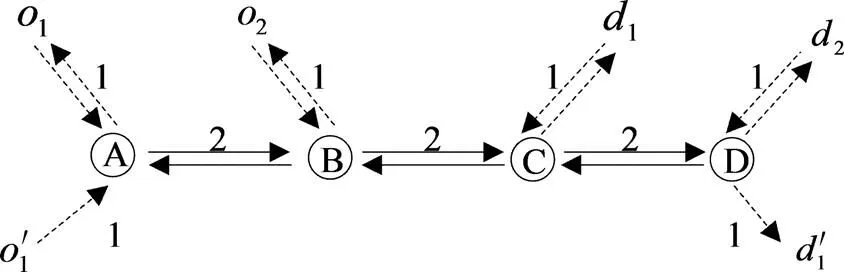
图1 4个物理节点的简易铁路线路

构建时间−空间网络,将时间划分成均等的时间间隔,每个时间间隔具有相同的时间长度。设旅客1的期望出发和到达时间窗分别是[3,6]和[11,14];旅客2期望出发和到达时间窗分别是[6,8],[12,15]。对于列车,设其最早离开起始站时间为1,最晚到达终到站时间为20。最短路径时空网络图如图2所示。
在此二维时空网络中,设定:1) 任何列车可处于任何物理节点或虚拟节点。2) 任意列车只能在其允许运行时间窗内运行。3) 乘客只能在其期望出发时间窗内上车,也只能在其期望到达时间窗内 下车。
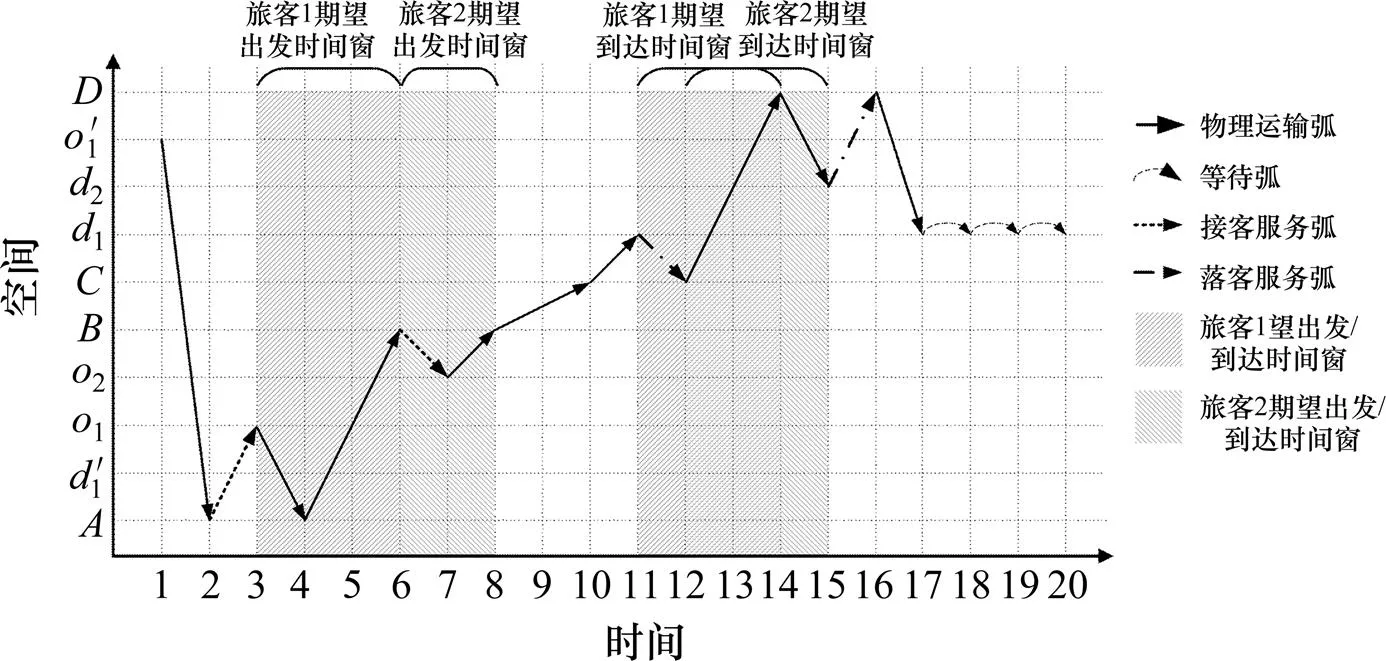
图2 最短路径时空网络图
1.2 运输状态的引入、表达与传递
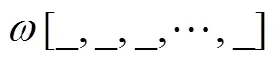

表1 时空状态网中相关参数及含义
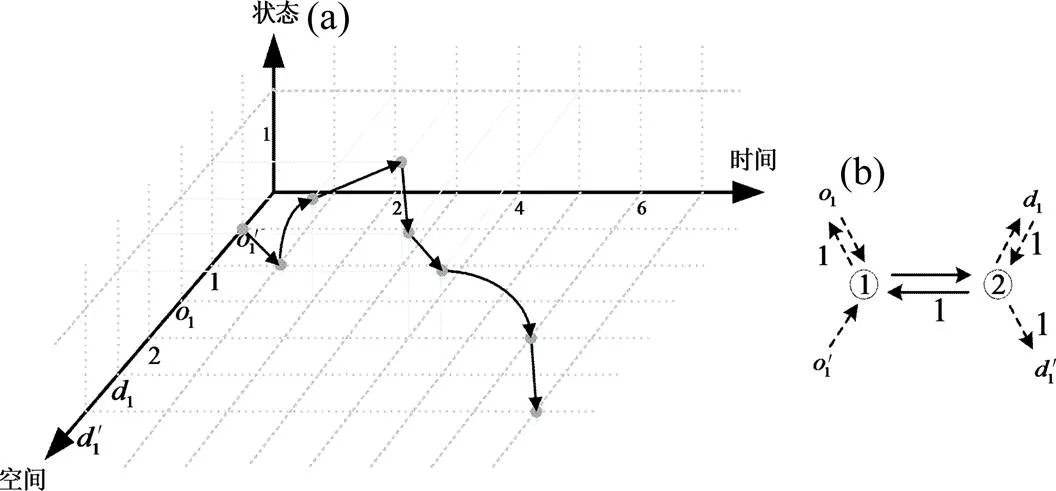
(a) 时空状态网络上的最短路;(b) 简易路网
将旅客组的运输状态引入时空网络后,二维时空网络由此转变为三维时空状态网络。三维时空状态网络中,每个点可表示为(,,)。简易线路下的三维时空状态网络上的最短路如图3所示。
2 数学模型
2.1 模型假设
1) 不考虑车底的运用、车站进路排列和到发线的运用;假定列车数量足够。
2) 列车均在双线铁路上运行,且只考虑单向行驶。
3) 自动闭塞区段,列车采用按闭塞分区追踪运行的行车组织方式运行。
4) 不考虑旅客的换乘行为。
2.2 列车停站方案与列车运行图综合优化数学模型
2.2.1 模型参数
模型参数及其含义见表2。

表2 模型参数及其含义
2.2.2 目标函数
在空间−时间−状态三维网络中,列车可从点(,,)通过弧(,,,,,′)到达点(,,′)。引入0-1变量(,,,,,,′)表示列车是否使用弧(,,,,,′)。(,,,,,,′)表示列车在弧(,,,,,,′)上的花费,定义其与列车运行时分成正比。本研究考虑的目标函数是最大限度减少列车花费,实现运营总费用最小化。定义列车在弧(,,,,,′)上的运营费用为(,,,,,,′),令该费用与旅行时间成正比。目标函数如下:
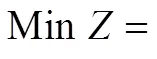

2.2.3 约束条件
第Ⅰ组约束:网络节点流量平衡约束
保证在任何时刻,每个节点上的列车流平衡,例如,假设在中间节点,任意列车在由时空网络上表示为(′,′,′)的点到达节点(,,)后,则此列车必有由节点(,,)到节点(′,′,′)的流动过程。因流平衡在始发节点、终到节点和中间节有所不同,对其进行如下约束。
1) 列车在始发车站的流量平衡约束:

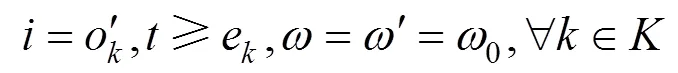
2) 列车在终到车站的流量平衡约束:
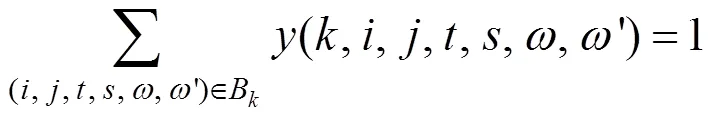
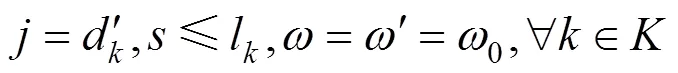
3) 列车在中间节点的流量平衡约束:
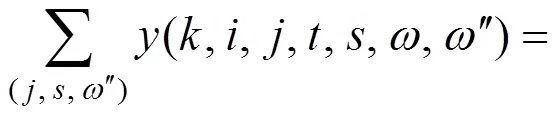
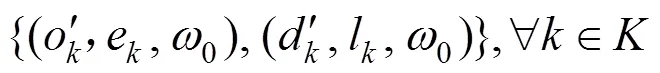
列车在物理节点上需同时满足进出服务弧、等待弧与物理弧守恒。
第Ⅱ组约束:旅客需求约束
4) 约束满足所有旅客均能在其起点搭乘列车,且均能搭乘列车到达终点:
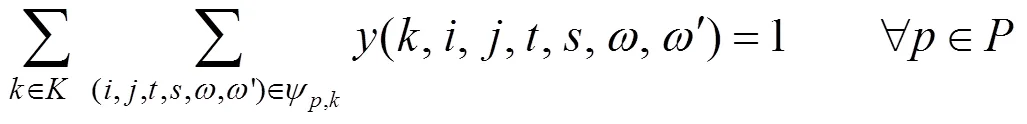
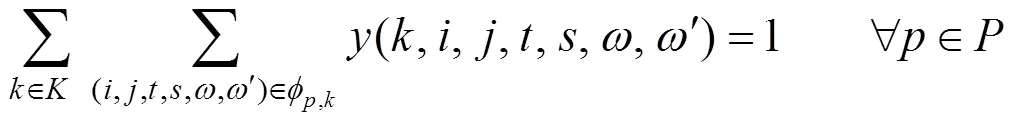
5) 同一旅客的接客和落客由同一列车承担:
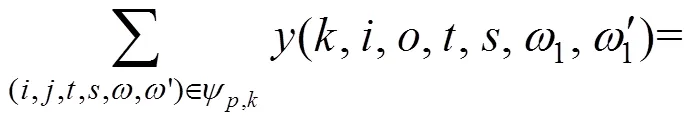
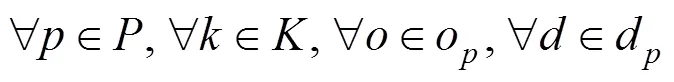
第Ⅲ组约束:列车运行约束
6) 区间运行时分约束、停站时间约束。列车在区间运行应大于列车在区间运行的最小运行时间;将虚拟的接客服务弧和落客服务弧以及与其相对应的物理节点与旅客虚拟节点相连的物理弧花费的最小时间作为列车停站时间:
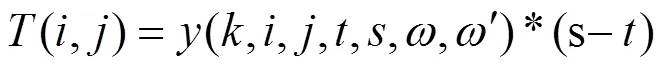
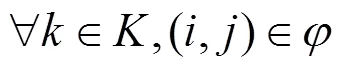
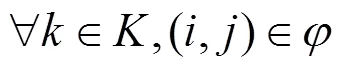
7) 追踪间隔时间约束。
约束表示在同一车站的某一时刻以及与其相隔最小发车时间间隔(,)内,最多有1列车出发;同一车站的某一时刻以及与其相隔最小到达时间间隔(,)内,最多有1列车到达;且当发车时间间隔不满足临界发车间隔时,列车通过等待弧等待,直到满足条件,以保证列车在区间的行车 安全:

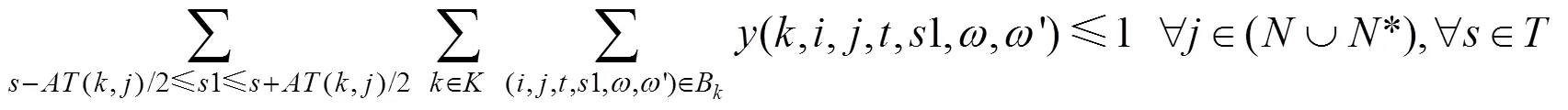
3 求解算法
Mahmoudi等[10]指出,模型中决策变量为多维变量时,此问题在现实中为较复杂问题,经证实,拉格朗日松弛算法可用来寻求较好的解。

目标函数为:
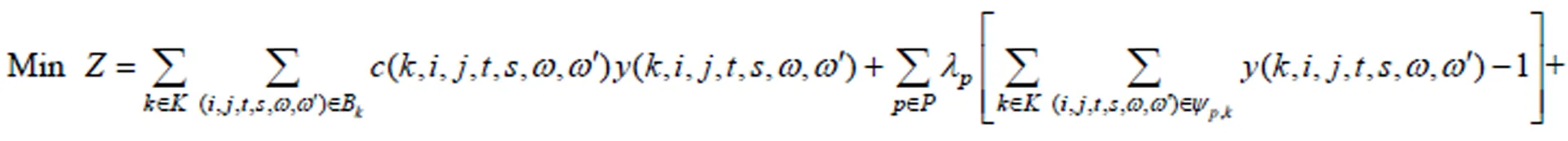
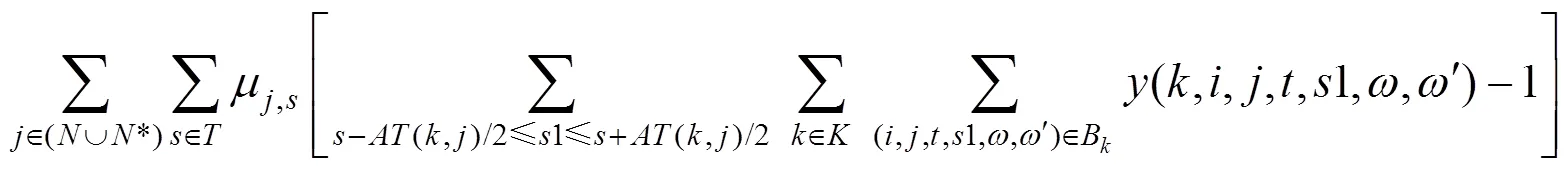
通过对式(13)进行恒等变换,可得到:
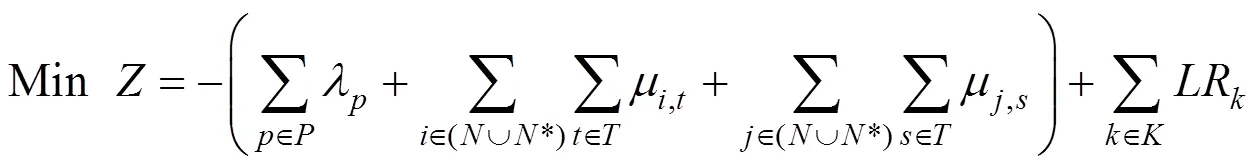
(14)
松弛后的目标函数式(12)可以分解为一个常数项与所有列车LR之和,如式(13)。式(13)中的LR由2部分组成,一部分为时间价格,表示列车占用时空资源的代价;另一部分为旅客上车约束、列车追踪间隔时间约束的拉格朗日乘子之和,可以看作列车不满足以上松弛约束时的惩罚值。由于约束(5),(10)和(11)被松弛,剩余约束均作用于单个列车,消除了各旅客组均需要被列车接送导致的列车间的相互影响,打破了各列车在占用行车资源时的关联关系,因此,该问题在数学规划中可以被分解为多个相互独立的列车子问题。该问题的目标函数是所有列车时空路径的目标函数LR之和,实质上是列车时空路径的最短路问题。因此,通过构建符合约束的时空状态网络,然后通过最短路算法即可求得该子问题的最优解。
上述松弛问题的解为原问题的下界,为了使其尽可能接近原问题的最优解需要求解以下拉格朗日松弛对偶问题:
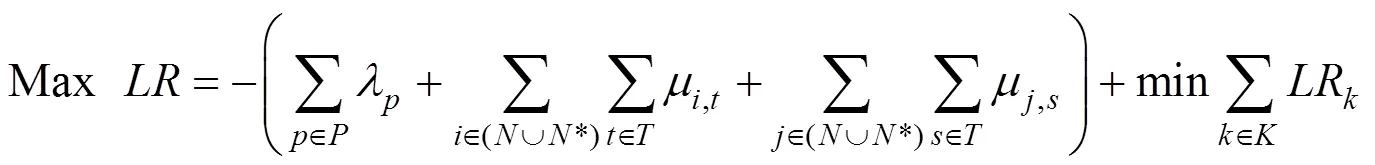
对于拉格朗日对偶问题,需要找到合适的拉格朗日乘子的值,使松弛问题的解尽可能接近原问题的最优解。采用迭代的方法,利用次梯度法迭代更新拉格朗日乘子,迭代公式如下:
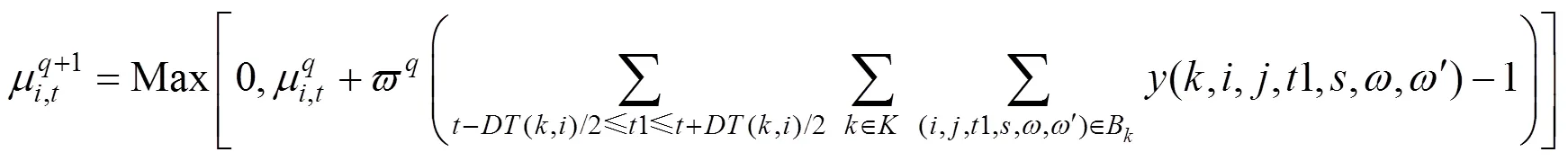
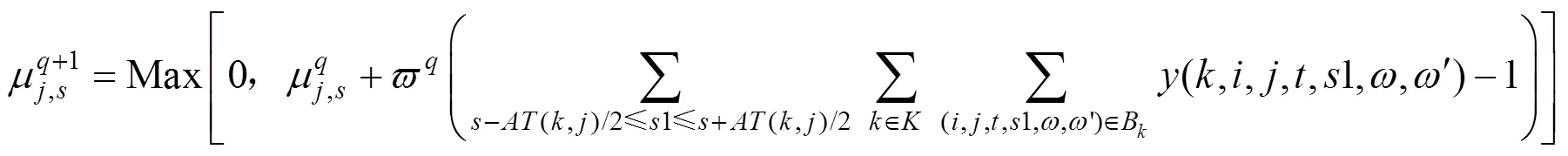
式(16)表示约束(5)的拉格朗日乘子与当前的拉格朗日乘子以及本次迭代求解得到的旅客组的列车访问次数有关;约束(11)的拉格朗日乘子与当前的拉格朗日乘子以及本次迭代求解得到的列车对时空资源的占用次数有关。因此,在求解过程中根据当前拉格朗日乘子、列车对旅客组的访问次数和对时空资源的占用次数更新对应的拉格朗日乘子。
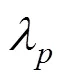
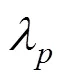
步骤2 求解拉格朗日松弛问题。
步骤2.1遍历每列待规划列车,对每列待规划列车执行以下步骤:
步骤2.1.1根据约束条件构建时空状态网络;
步骤2.1.2求解列车从起始站到终点站在时空状态网络中的最短路径(参考文献[3]的基于动态规划的时空状态网络最短路算法),对列车访问的节点进行标记;
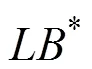
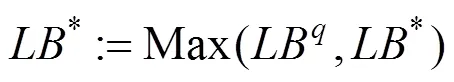
其中:LB为第次迭代松弛问题的下界值
步骤2.3次梯度法更新拉格朗日乘子。
步骤2.3.1根据式(18)更新旅客组的列车访问次数
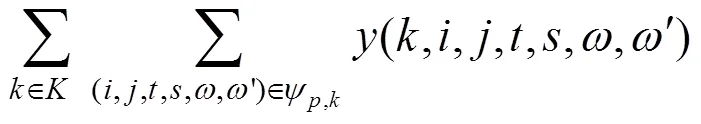
步骤2.3.2根据式(19)更新节点的列车访问次数
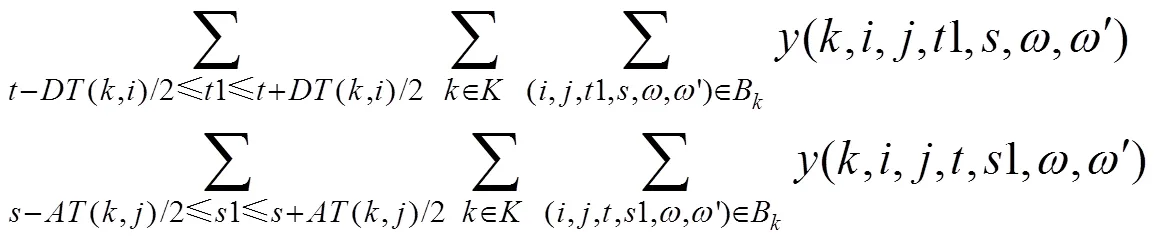
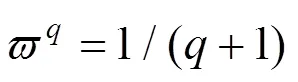
步骤2.4清空时空状态网络中的节点占用标记;
步骤3 求解可行解。
步骤3.1根据式(21)按照各列车涉及的拉格朗日乘子和LRP将各列车从大到小排序;
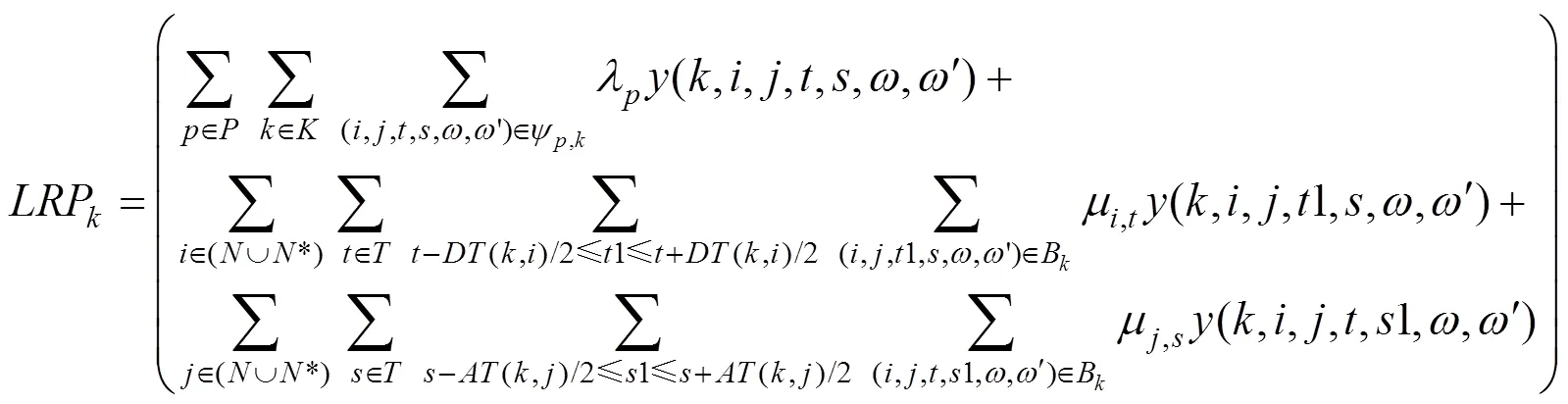
步骤3.2遍历排序后的每列待规划列车,按照LRP从大到小的顺序对每列待规划列车执行以下步骤:
步骤3.2.1根据约束条件及节点占用标记构造时空状态网络;
步骤3.2.2求解列车从起始站到终点站在时空状态网络中的最短路径(参考文献[3]的基于动态规划的时空状态网络最短路算法),对列车访问的节点进行标记;
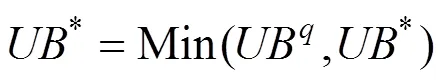
步骤3.4清空时空状态网络中的节点占用 标记;
4 案例分析
本文以京沪高铁北京南−曲阜东区段(选用8座车站:北京南、廊坊、天津南、沧州西、德州东、济南西、泰安和曲阜东)为例进行案例分析。根据实际的京沪高铁运行图,算例截取区间最小运行时分、最小停站时分(1 min)、列车最小发车间隔(3 min)、列车最小到达间隔(3 min)。列车定员为1 000人,有取舍的分别设立90个旅客组。设定时间铺划单位为1 min,时间长度为180 min。
为了验证数学模型是否能有效的满足旅客需求,算例分别设置2个数据集:数据集①是基于现实铁路客票系统售票数据的旅客数据;数据集②是均衡旅客流数据。基于上述数据集,设置两组对照试验:
对照试验1:对比数据集①和数据集②下得出的列车运行图对旅客需求的满足程度及其随旅客需求的变化。
对照试验2:对比按阶段编制得出的列车运行图目标函数值与模型求解得出的目标函数值(采用数据集①)。
数据集①和②下得出的列车运行图如图4~5所示;按阶段编制列车运行图如图6所示;不同情形目标函数值的对比如图7所示。
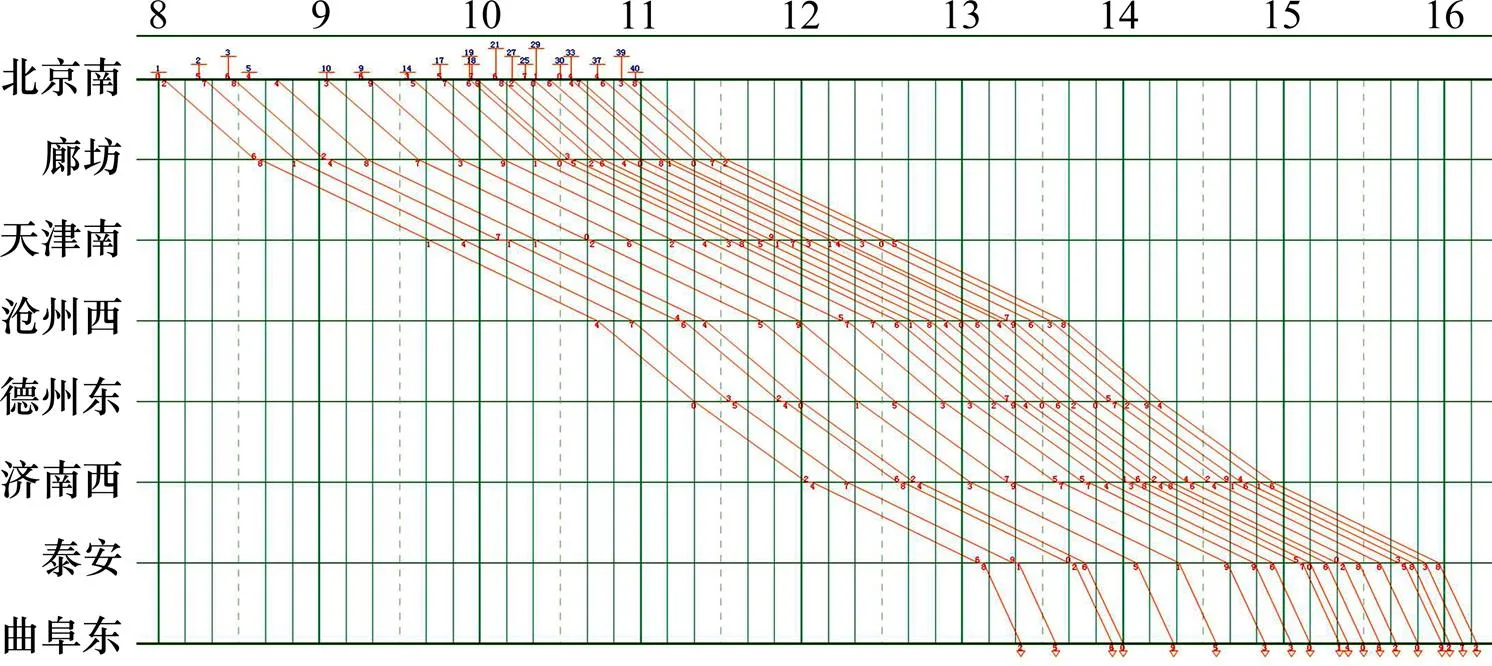
图4 基于现实铁路客票系统售票数据下编制的列车运行图
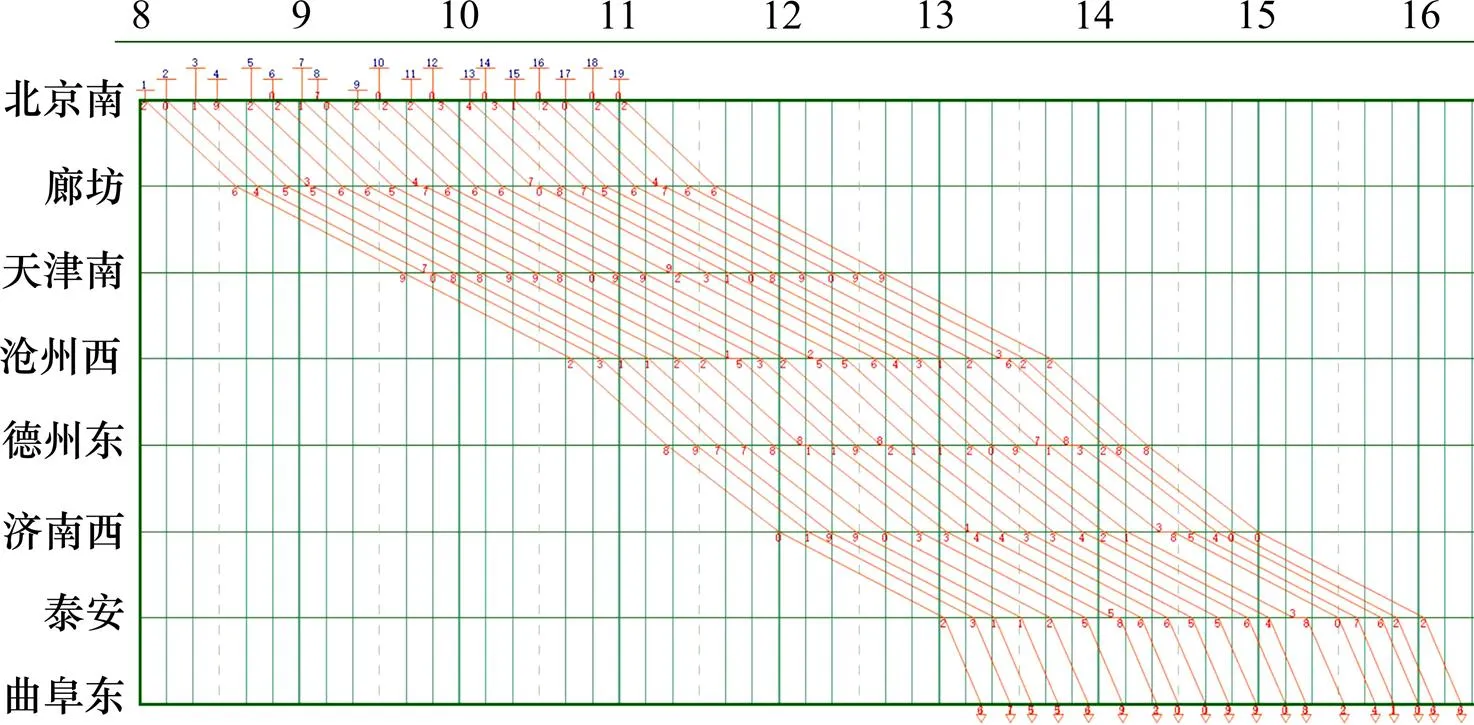
图5 均衡客流数据下编制的列车运行图
由求解结果可做出如下分析:
1) 模型求解得到的列车时刻表与运输状态相对应,在铁路花费较小的目标函数下,数据集①和②下的算例结果显示旅客的需求得到满足,模型的有效性得到证明。
2) 2个数据集下得到的列车运行图中,列车开行的疏密程度、列车停站方案均与旅客需求相对应:说明本研究中的列车运行图编制模型能够根据旅客需求数据灵活的设立列车停站模式和铺画列车时刻表。
3) 由对照实验2的结果(图6)可以看出,一体化编制模型下的目标函数与按阶段编制的目标函数相比,目标函数值降低了9.5%,证明一体化编制模型在求解时刻表问题上具有良好的适用性,也体现了一体化编制对比分阶段编制所呈现出的优势。
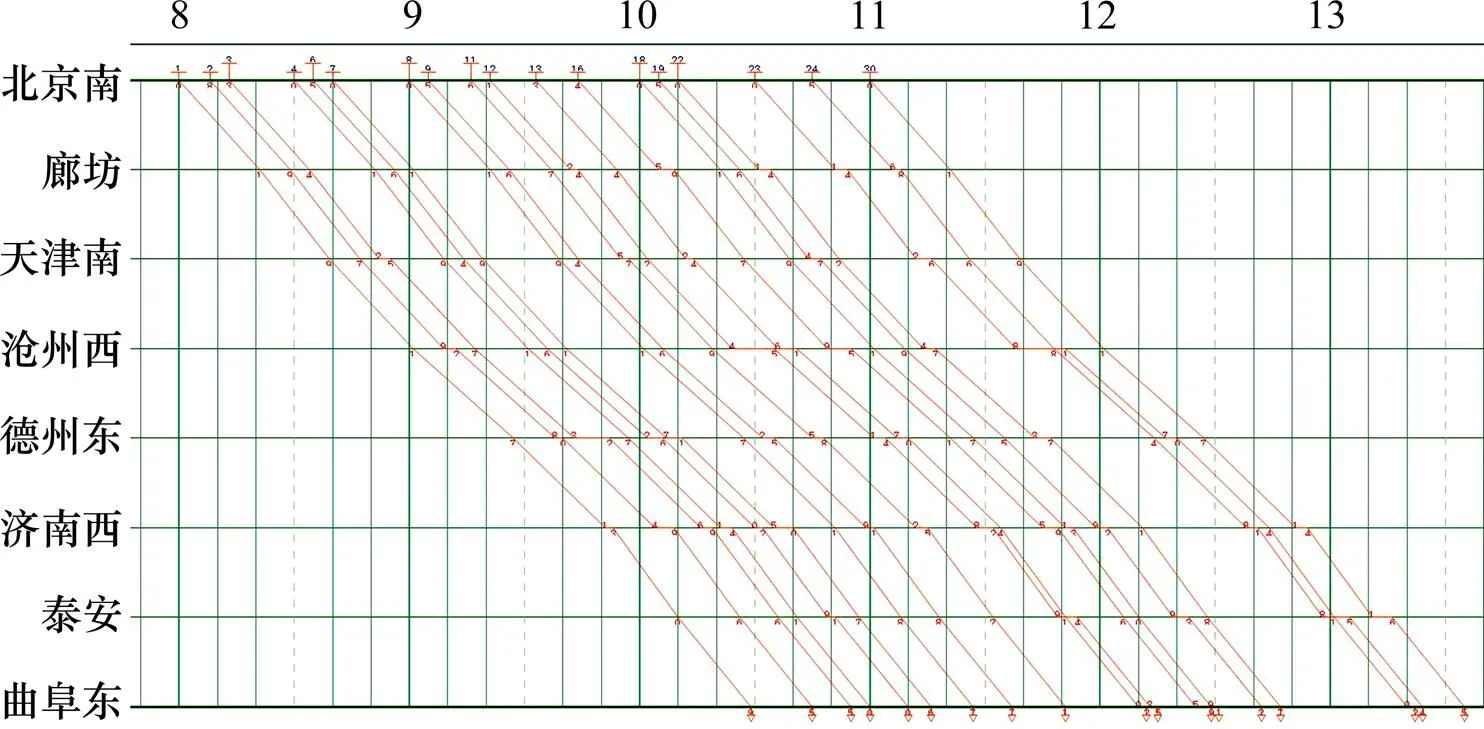
图6 按阶段编制列车运行图
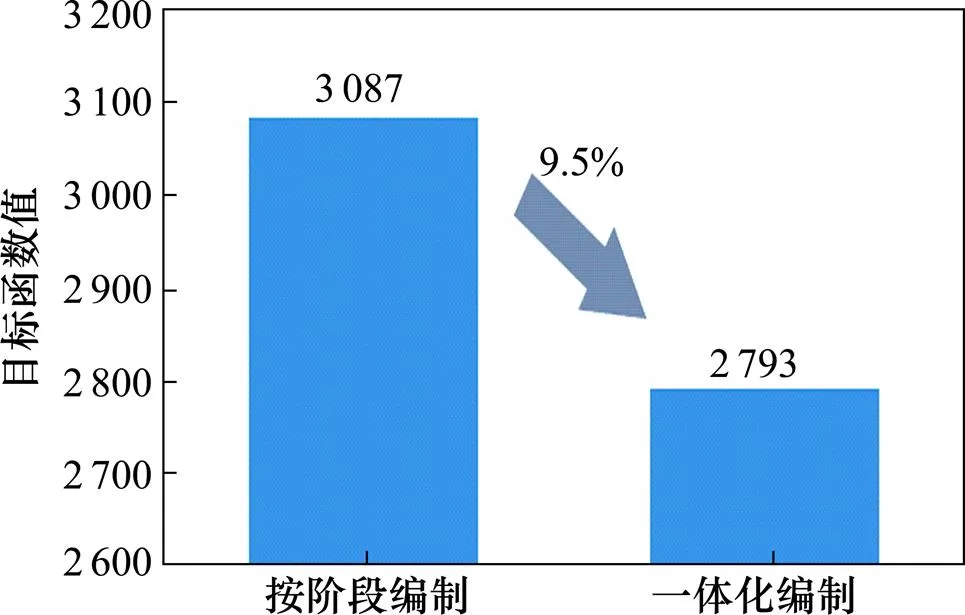
图7 不同情况下的目标函数值对比
5 结论
1) 考虑高速铁路旅客出行的时空敏感性较高的特点,通过将旅客运输状态引入时空网络,构建三维的时间−空间−状态网络,运用网络流理论,实现了旅客分配、停站方案与列车运行图的一体化优化。通过设计拉格朗日松弛求解算法,将复杂的列车间强耦合问题分解为单列车的最短路径子问题集合,降低了模型求解难度。
2) 对比非均衡客流与均衡客流数据下的模型结果,证实了模型不仅能够满足旅客需求,而且能够在线路花费较小的前提下,根据客流需求密度的变化,实现停站方案、列车运行图一体化优化;对比分阶段编制列车运行图模型与一体化编制列车运行图模型得到的目标函数值,体现了一体化编制的适用性及优势。
3) 本文的研究仍然具有一定的可扩展性。在旅客需求方面,需要进一步考虑各种交通方式背景下的旅客自主选择。在求解方面,对于大规模的问题需要进一步改进算法来提高求解速度。
[1] 史峰, 黄铮诚, 周文梁, 等. 基于用户平衡分析的旅客列车始发时间分布优化[J]. 铁道科学与工程学报, 2008, 5(6): 69−75. SHI Feng, HUANG Zhengcheng, ZHOU Wenliang, et al. Optimization of passenger train origin time distribution based on user equilibrium analysis[J]. Journal of Railway Science and Engineering. 2008, 5(6): 69−75.
[2] 黄鉴, 彭其渊. 基于分时客运需求的客运专线列车运行图优化[J]. 铁道科学与工程学报, 2012, 9(6): 66−71. HUANG Jian, PENG Qiyuan. Passenger dedicated line operation diagram optimization based on timeshare passenger demand[J]. Journal of Railway Science and Engineering, 2012, 9(6): 66−71.
[3] Robenek T, Maknoon Y, Azadeh S S, et al. Passenger centric train timetabling problem[J]. Transportation Research Part B: Methodological, 2016, 89: 107−126.
[4] 黄鉴. 基于旅客动态调整的客运专线网络列车开行方案优化研究[D]. 成都: 西南交通大学, 2013. HUANG Jian. Research on optimization of passenger dedicated line network train operation plan based on passenger flow dynamic adjustment[D]. Chengdu: Southwest Jiaotong University, 2013.
[5] NIU H, ZHOU X, GAO R, et al. Train scheduling for minimizing passenger waiting time with time-dependent demand and skip-stop patterns: Nonlinear integer programming models with linear constraints[J]. Transportation Research Part B: Methodological, 2015, 76: 117−135.
[6] Kaspi M, Raviv T. Service-oriented line planning and timetabling for passenger trains[J]. Transportation Science, 2013, 47(3): 295−311.
[7] 周文梁, 秦进, 邓连波, 等. 城市轨道网络列车运行计划实施效果综合评价[J]. 铁道科学与工程学报, 2014, 11(1): 118−125. ZHOU Wenliang, QIN Jin, DENG Lianbo, et al. Comprehensive evaluation of implementation effect of urban rail transit network train operation plan[J]. Journal of Railway Science and Engineering, 2014, 11(1): 118− 125.
[8] 周文梁. 客运专线网络列车开行方案与运行图综合优化模型及算法[D]. 长沙: 中南大学, 2010. ZHOU Wenliang. Comprehensive optimization model and algorithm of train operation plan and operation diagram for passenger dedicated line[D]. Changsha: Central South University, 2010.
[9] 周文梁, 史峰, 陈彦, 等. 客运专线网络列车开行方案与运行图综合优化方法[J]. 铁道学报, 2011, 33(2): 1−7. ZHOU Wenliang, SHI Feng, CHEN Yan, et al. A comprehensive optimization method for operation plan and operation diagram of passenger dedicated line network[J]. Journal of the China Railway Society, 2011, 33(2): 1−7.
[10] Mahmoudi M, ZHOU X. Finding optimal solutions for vehicle routing problem with pickup and delivery services with time windows: A dynamic programming approach based on state-space-time network representations[J]. Transportation Research Part B: Methodological, 2016, 89: 19−42.
Integrated optimization of stopping pattern and train timetable for passenger demand
LIU Lu1, MENG Lingyun1, LI Xinyi1, LIU Gang2
(1. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China; 2. Tianjin Nanhuan Railway Maintenance Co., Ltd, Tianjin 300381, China)
Considering the space-time sensitivity of high-speed railway passengers, we introduced a passenger carrying state to expand the two-dimensional transport space-time network into a three-dimensional network which is called space-time-state network. An integrated optimization model of stopping pattern and train timetable for passenger demand was proposed to realize the integration of passenger distribution, stopping pattern selection and train timetabling. The Lagrange relaxation algorithm was designed to decompose the complex train coupling problem into the shortest path sub-problem of a single train, so as to reduce the difficulty of solving the model. Computational experiments were performed on a realistic case study based on a heavily used part of the Beijing-Shanghai high-speed railway. The results provide evidence that the integrated optimization model not only get a low operational cost, but also realize the integration of passenger distribution, stopping pattern selection and train timetabling.
railway transportation; train timetabling; Lagrangian relaxation algorithm; integrated optimization; space-time-state network; passenger demand
10.19713/j.cnki.43−1423/u.2019.02.031
U292.41
A
1672 − 7029(2019)02 − 0518 − 10
2018−03−16
国家自然科学基金面上资助项目(71571012);中央高校基本科研业务费专项资金资助项目(2017JBM029);大型枢纽机场旅客捷运系统关键技术研究与应用(民航科技项目任务-编号:201501)
孟令云(1983−),男,河北迁安人,副教授,博士,从事列车运行图编制等研究;E−mail:lymeng@bjtu.edu.cn
(编辑 阳丽霞)
