基于6σ的动车组转向架构架非概率可靠性分析

智鹏鹏，陈秉智，李永华，宋雪萍



基于6的动车组转向架构架非概率可靠性分析

智鹏鹏1，陈秉智2，李永华2，宋雪萍1

(1. 大连交通大学 机械工程学院，辽宁 大连 116028； 2. 大连交通大学 机车车辆工程学院，辽宁 大连 116028)

针对转向架构架静强度实验结果仅对测试件有效，不能准确反映整批构架的结构强度是否满足要求的问题，提出一种基于6的非概率可靠性分析方法。首先，通过对转向架构架进行结构强度分析，确定受力较大部位的区间变量，并基于参数化模型对其进行D-最优试验设计，建立表征转向架构架结构特征的多项式响应面函数。其次，结合6原则和Chebyshev不等式，建立描述区间变量的分段函数模型，给出新模型中区间变量的生成策略和非概率可靠度的计算方法。最后，以动车组转向架构架为研究对象，对其进行结构可靠性分析，并与传统的分析方法进行对比。研究结果表明：在信息缺乏或小样本的条件下，分段函数模型更好地反映整批构架的结构可靠性，弥补了基于均匀分布假定相对保守的缺陷，同时，解决了由测试次数少导致的实验结果的局限性。

转向架构架；非概率可靠性；D-最优试验设计；6原则；Chebyshev不等式

转向架构架作为动车组主要的承载部件，不仅是各组成的安装基础，而且具有传递载荷、固定车轴位置的作用，其结构的可靠性和安全性成为列车速度不断提升的重要保障[1]。然而，转向架构架作为大型的复杂产品，其静强度测试成本较高、测试次数少导致实验结果具有很大的局限性，仅能反映被测件的结构强度。因此，为了解批量化生产的构架的结构强度能否满足要求，提高动车组转向架构架的设计水平，对其进行结构可靠性分析是十分必要的。在转向架构架的实际设计和运营过程中，结构尺寸由于受到加工制造水平的限制，并不能保证所有构架的焊接板材尺寸的一致性，而是存在一定的加工误差；而且运行线路的复杂性及客流量的波动性使得构架所承受载荷具有随机性。通常，在处理这些不确定因素时采用随机可靠性和模糊可靠性分析方法，即概率模型和模糊模型[2]。采用概率模型的前提是获得不确定变量的概率分布特征，进而得到变量的概率密度函数；采用模糊模型的前提是已知不确定变量的隶属度函数。然而，对于动车组转向架构架而言，结构复杂程度较高、实际运行环境复杂，结构尺寸和载荷的统计数据缺乏导致获取不确定变量的统计特征较为困难[3−5]。正是由于这些局限性的存在，部分学者将目光转移到了非概率的集合模型。Ben-haim等[6−7]提出当数据不足时，应采用凸集模型来描述不确定性。郭书祥等[8−11]提出基于区间模型的可靠性分析方法、非概率可靠性度量方法、非概率可靠性指标和区间模型安全系数之间的解析关系以及基于区间变量的可靠性优化设计方法。区间分析作为上述非概率可靠性分析方法之一，由于仅需要输入不确定变量的区间参数，即可得到响应值，被广泛应用于工程实际中。但是常规区间分析是基于区间变量服从均匀分布的假定，计算出的可靠度值过于保守，不能准确估计产品的结构可靠性，造成制造成本的增加，而且区间分析中区间运算的计算效率低，对多设计变量的模型求解不适用。在转向架构架静强度和动力学研究的基础上[12−15]，本文以某动车组转向架构架为研究对象，综合考虑工程实际中设计参数的不确定性，采用D-最优试验设计选取参数化模型的样本点组合，建立高精度的响应面函数。将Chebyshev不等式和6原则融入区间数中，建立描述区间变量的分段函数新模型。结合响应面函数和分段函数模型给出结构非概率可靠度的计算方法，并对比分段函数、均匀分布和正态分布下转向架构架的可靠度。该方法不仅能够弥补均匀分布假定的可靠性分析过于保守的缺陷，而且提高了运算效率；相比概率分布假定减少了对数据信息的需求量。

1 转向架构架区间变量的确定

区间变量是非概率可靠性分析的基础，对于动车组转向架构架，区间变量的选择是构造该结构响应面函数的前提。本文采用对动车组转向架构架进行静强度分析的方法确定构架的区间变量。

研究所采用的转向架为某型号城际动车组转向架，转向架构架主要由侧梁、横梁以及各种吊座组成，几何模型如图1所示。

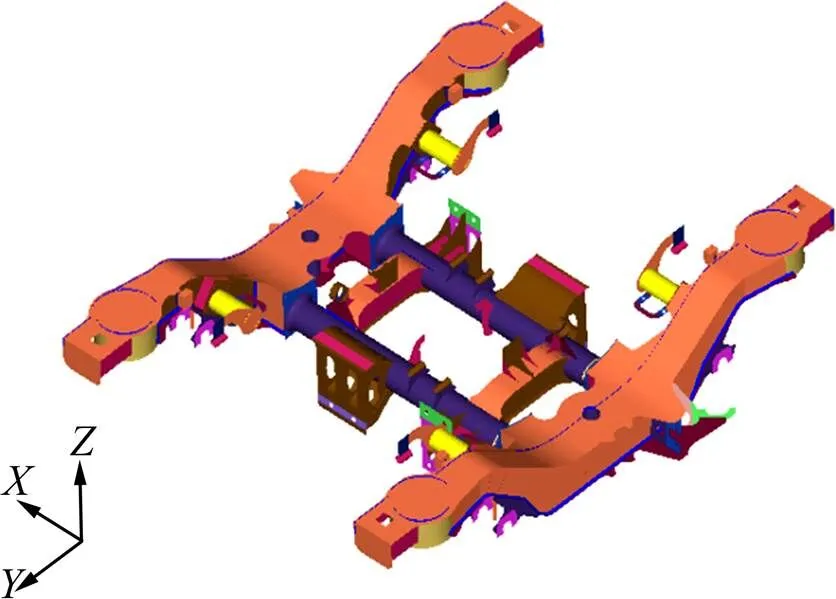
图1 转向架构架几何模型

为方便构造结构响应面函数，动车组转向架构架整体采用Shell181壳单元进行网络划分，节点总数为49 544个，单元总数为52 927个。分别采用Rbe3单元模拟螺栓连接，Spring单元COMBIN14模拟弹簧连接，各种悬挂设备均取其中心位置通过Rbe3单元与座体相连。按照动车组转向架构架的静强度评定标准对其施加载荷，转向架构架的最大应力取有限元分析结果的最大节点等效应力，构架的应力云图如图2所示。

图2分别为动车组转向架构架的轴侧、正面、反面和侧面的应力云图。根据图2的分析结果可知，构架承受的最大应力在齿轮箱吊座与横梁连接的筋板处，Von.Mises应力为266.9 MPa。通过对转向架构架进行受力分析可知，侧梁的上下盖板、横梁、筋板以及载荷对其受力的影响较大。可将其作为动车组转向架构架的区间变量。

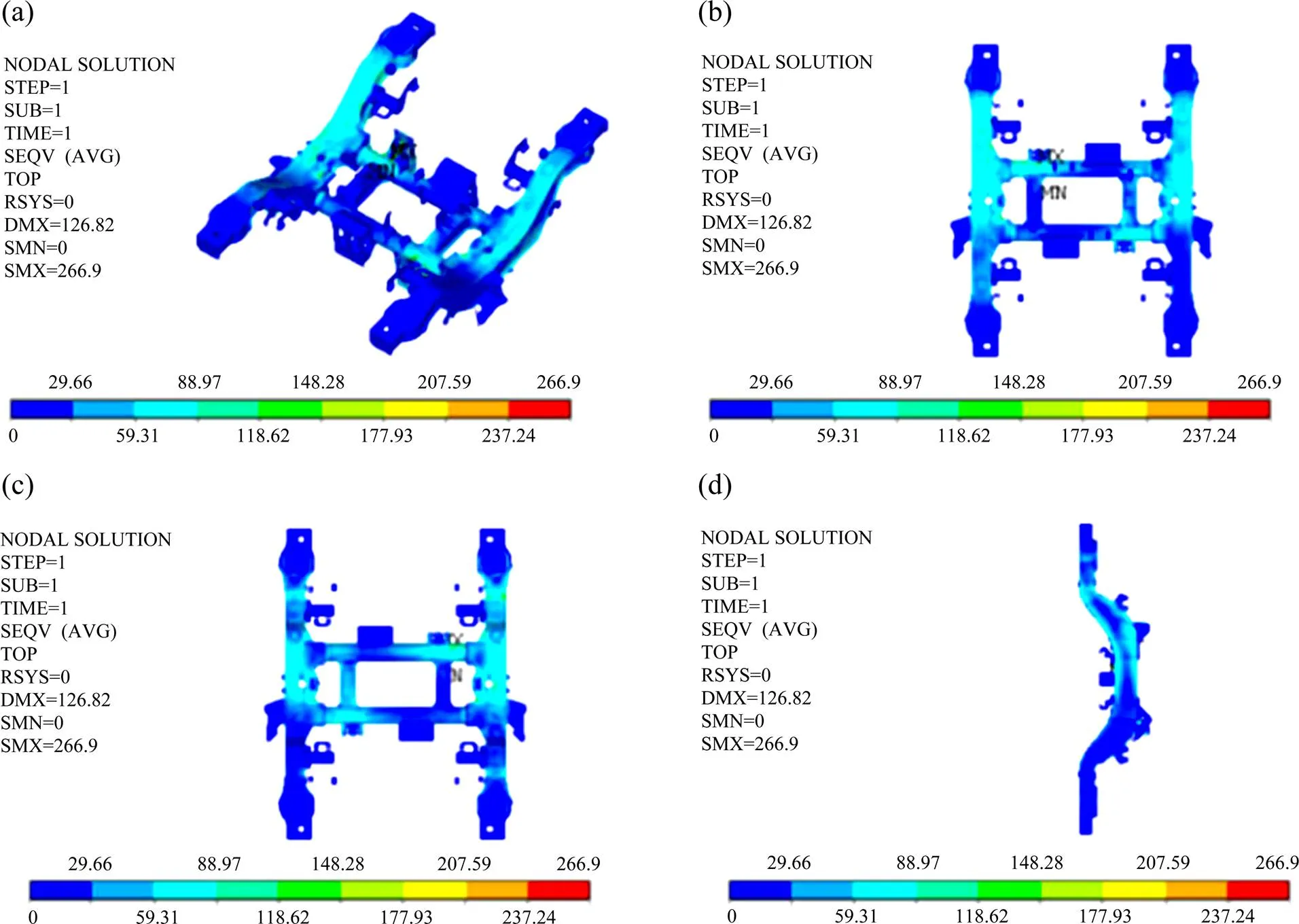
(a) 轴侧图；(b) 正面主视图；(c) 反面主视图；(d) 侧视图

2 转向架构架结构响应面函数的建立

动车组转向架构架机械结构复杂，精确的力学模型难以求得。为提高计算效率，采用响应面法近似获得表征转向架构架结构特征的函数，其优点在于能够将试验设计和有限元分析相结合，通过较少的计算在局部范围内比较精确的逼近函数关系[16]。

采用二次多项式的响应面函数在点(10，20，…，x0)处按泰勒级数展开，可以表示为

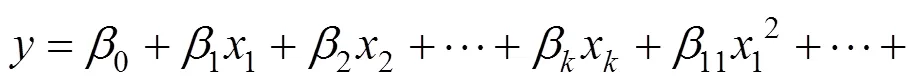
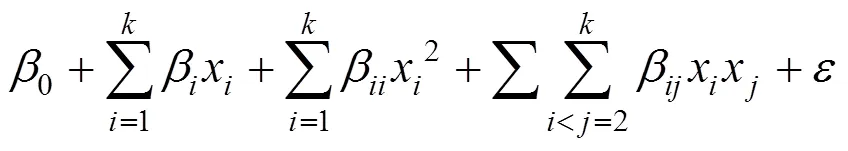
式中：为残差；x为设计参数；0，β，β和β为待定系数，一般采用最小二乘法估计获得。

为了提高拟合精度，采用D-最优试验设计的方法确定式(1)的样本点。无论因变量与自变量之间存在何种回归关系，可设其回归模型为：

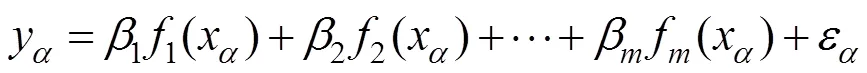
式中：x是给定的因子区域中一点，若因子空间为维欧氏空间，则x为维向量：(x，x，…，x)；1(x)，2(x)，…，f(x)为连续函数；β，β，…，β为个待定系数；ε为服从正态分布的随机变量。

若试验方案是由个试验点1，2，…，x组成，则可以得到式(1)的参数估计

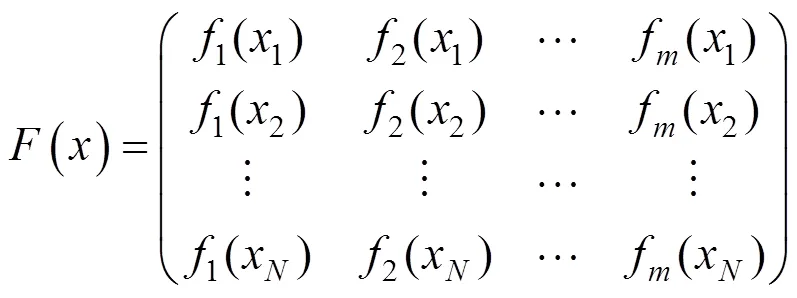
信息矩阵为

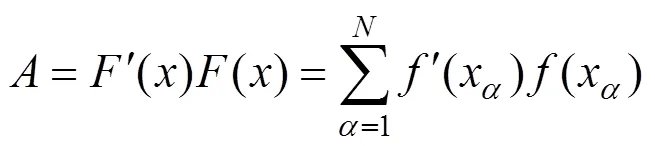
D-最优设计就是使得信息矩阵的值达到极大化的一种设计。

D-最优试验设计可以使回归系数的估计值1，2，…，b的方差所构成的密集椭球体的体积最小化，同时可以使模型回归预测值方差最大值达到最小。

3 区间变量的分段函数描述

3.1 Chebyshev不等式和6σ原则

根据概率理论，设随机变量的数学期望()与方差()存在，则对于任意正数，有不等式

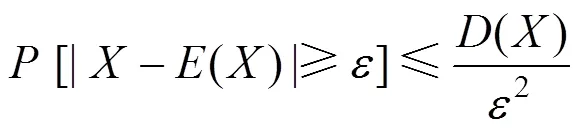
或

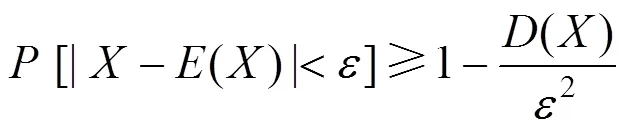
式(5)和式(6)称之为Chebyshev不等式[17]。

6设计方法(Design For Six Sigma, DFSS)是在这一评估产品波动情况的统计量的基础上，结合可靠性理论和容差模型设计方法，以6原则作为产品质量均值波动的范围，在满足各设计要求的情况下，使产品的可靠度达到99.999 999 8%[18]。正态分布下的不同值范围所对应的可靠度如图3 所示。

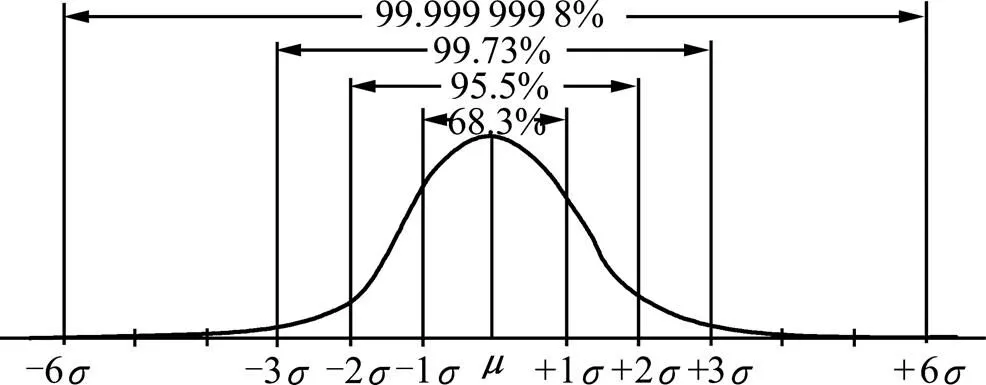
图3 6σ正态分布

3.2 分段函数模型

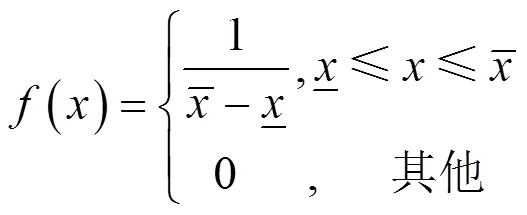
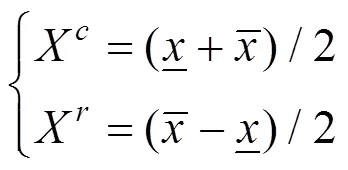
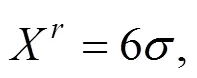
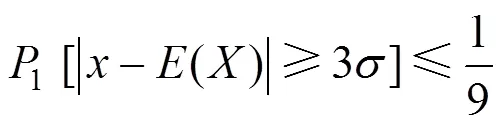
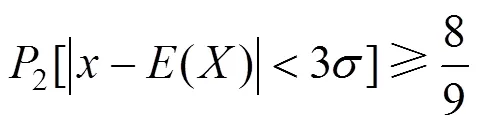
由式(9)和图3可得

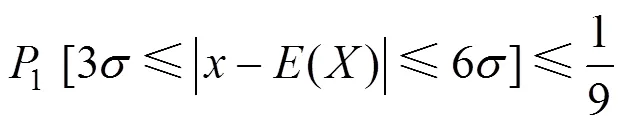
对转向架构架进行分析时，区间变量的离散程度按照偏保守处理，即取分布概率的临界值作为评判标准，则

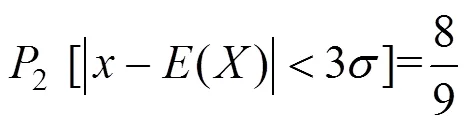
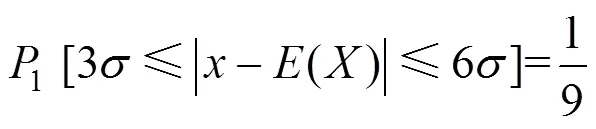
若区间变量在各个区间段均服从均匀分布，则分段函数区间变量的概率密度函数可表示为

分段函数描述的概率密度函数如图4所示。

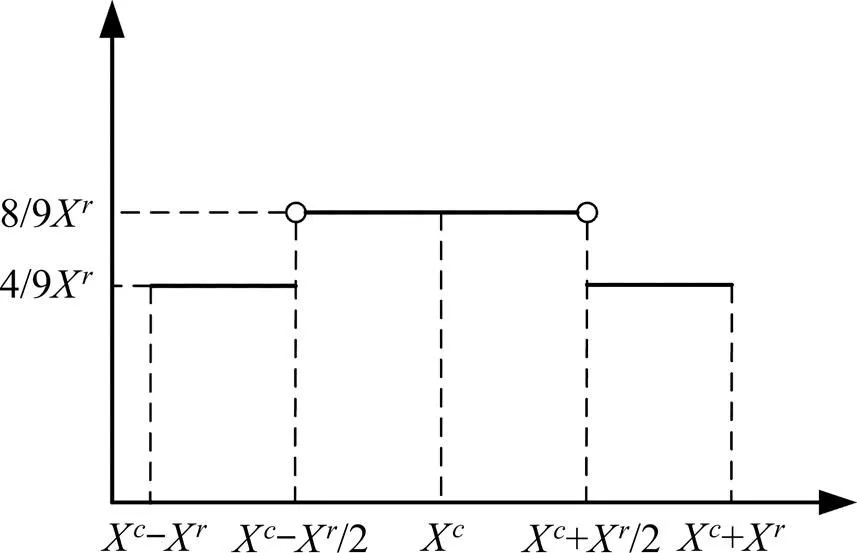
图4 分段函数描述的概率密度图

若将服从分段函数与均匀分布下的概率值进行对比可得到

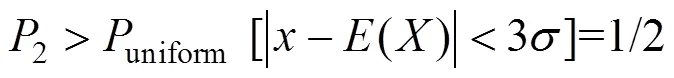
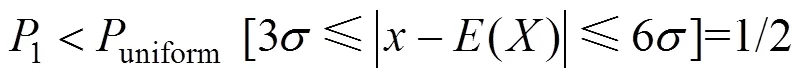
根据式(15)和(16)可知，分段函数模型相比区间均匀分布，使得区间变量的取值更加接近均值，这也与设计加工过程中，努力控制可控因素，力求偏差最小相符合。

4 非概率可靠度分析方法

4.1 分段函数区间变量的生成

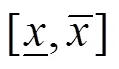
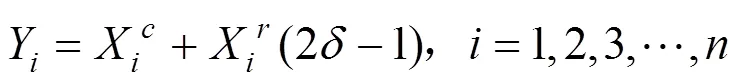
式中：为[0,1]上的随机数。

对每一个生成的Y进行分段函数的区间数 判断：

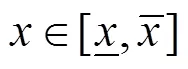
4.2 非概率可靠度计算方法

将产生的区间变量进行随机组合并代入转向架构架的结构响应面函数，计算区间变量波动下的构架的应力值，并基于极限状态方程对构架进行可靠性分析。

转向架构架结构可靠性分析的极限状态方程定义为

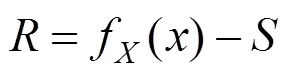
根据式(18)，可靠度可定义为

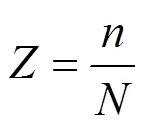
式中：为≤0的次数；为计算总次数。

4.3 非概率可靠性分析流程

基于6的动车组转向架构架非概率可靠性分析流程如图5所示。

根据图5可知，非概率可靠性分析的基本流程分为响应面函数的建立，区间变量的生成，非概率可靠度计算3部分。响应面的拟合精度是可靠性分析的前提；区间变量的生成保证了变量遵循6原则，且与工程实际中不断提高工艺水平相吻合；非概率可靠度计算给出了区间变量波动下构架的可靠度值，该值反映整批构架的结构强度能否满足要求。

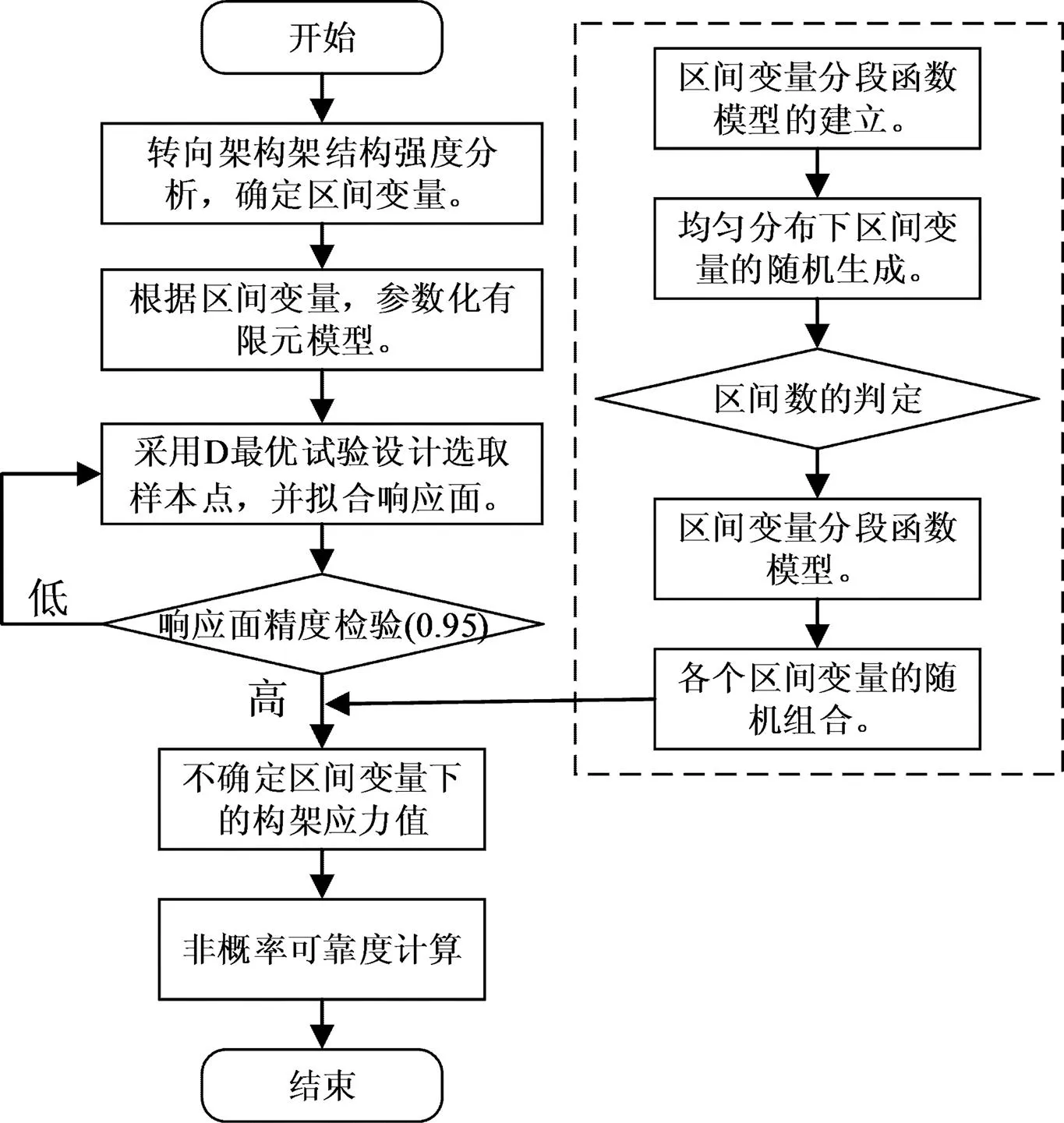
图5 非概率可靠性分析流程图

5 动车组转向架构架非概率可靠性分析

5.1 转向架构架的结构响应面函数

根据以上确定的区间变量，并考虑其实际生产过程中的上下偏差，利用D-最优试验设计选取样本点，区间变量应根据试验设计分为3个水平，见 表1。

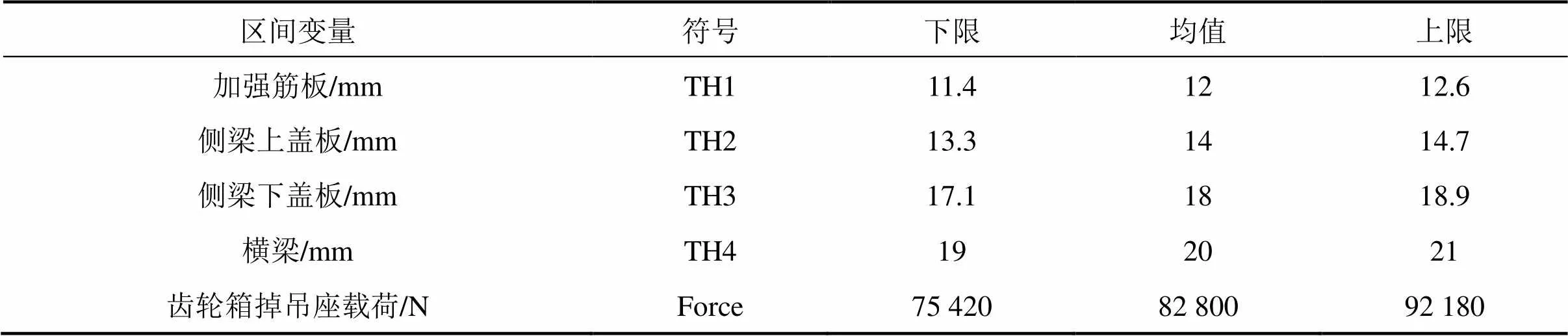
表1 区间变量水平特征

依据区间变量的实际结构尺寸及上下偏差，运用APDL语言对动车组转向架构架进行参数化设计，试验设计过程见表2。

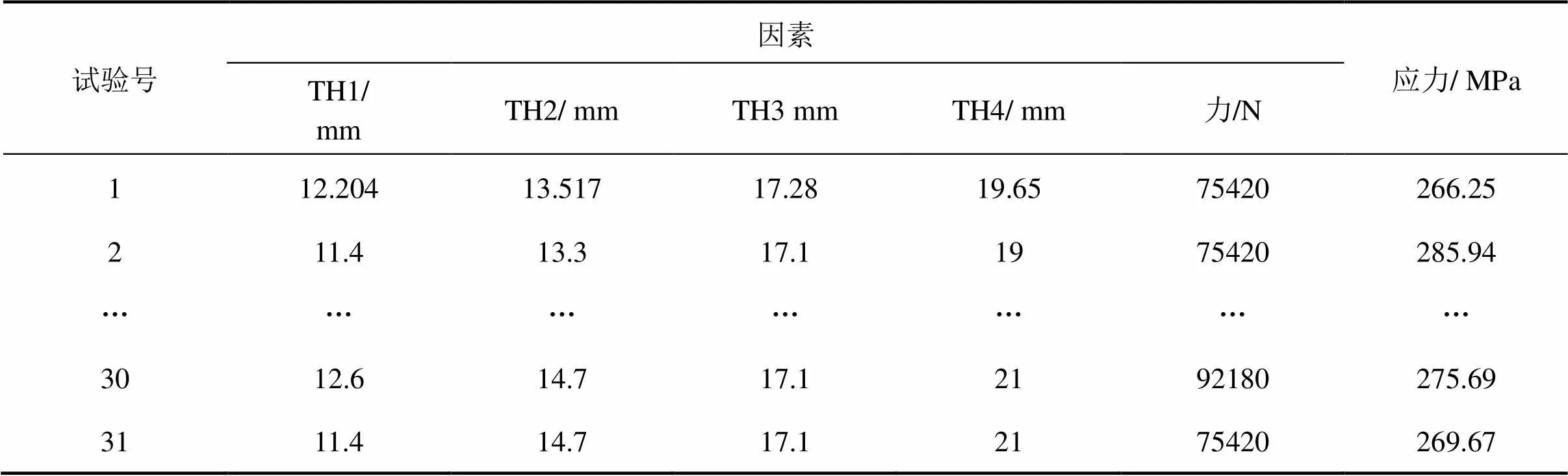
表2 区间变量试验设计过程

根据表2中的试验数据，利用最小二乘法原理拟合二次项系数，得到动车组转向架构架响应面函数的表达式为

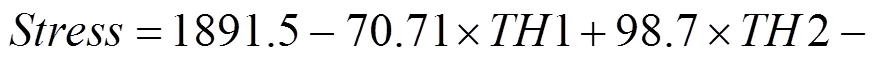
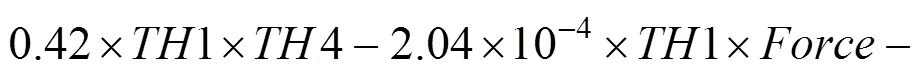
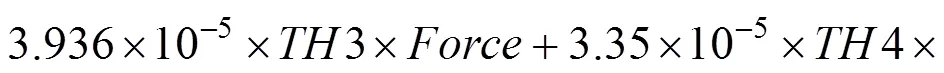
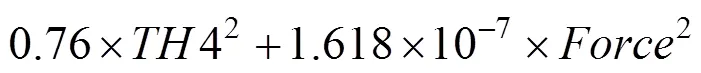
为了检验响应面函数的拟合精度，提高分析结果的准确性，将表1中的基本参数代入响应面函数得到最大应力为272.24 MPa，相比图2给出的266.9 MPa误差为2%。响应面函数的测定系数2为0.999 4，说明拟合程度较高，图6为拟合响应面函数的精度曲线。

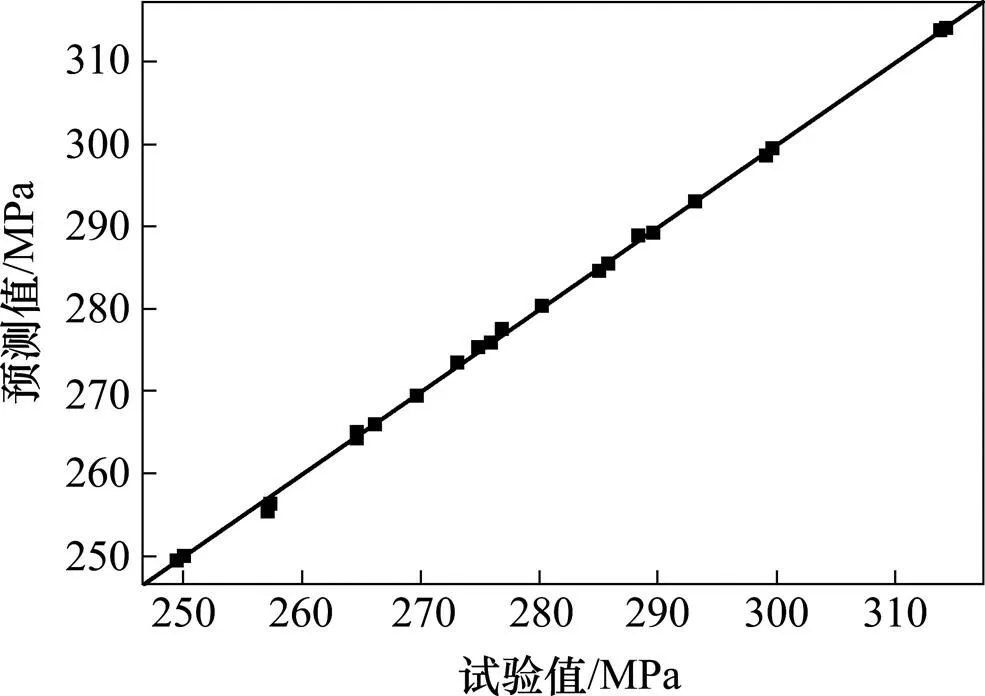
图6 试验值和预测值的相关图

由图6可以看出，试验值和预测值基本吻合，拟合精度和测定系数保持一致，拟合程度较好。

5.2 基于分段函数的构架非概率可靠度计算

根据4.1节区间变量的生成规则，利用MATLAB 2015b对各个区间变量分别取100个样本点生成基于分段函数的区间变量，如图7所示。

按照4.2节的方法，利用MATLAB 2015b对生成的分段函数区间变量进行1 000次随机组合，并将其代入式(18)~(20)得到转向架构架的结构可靠度值，如图10所示。为了验证该模型的准确性和实用性，将可靠度值分别与变量服从概率分布和均匀分布下的可靠度值进行了对比，图8和图9为概率分布和均匀分布下的区间变量取值。

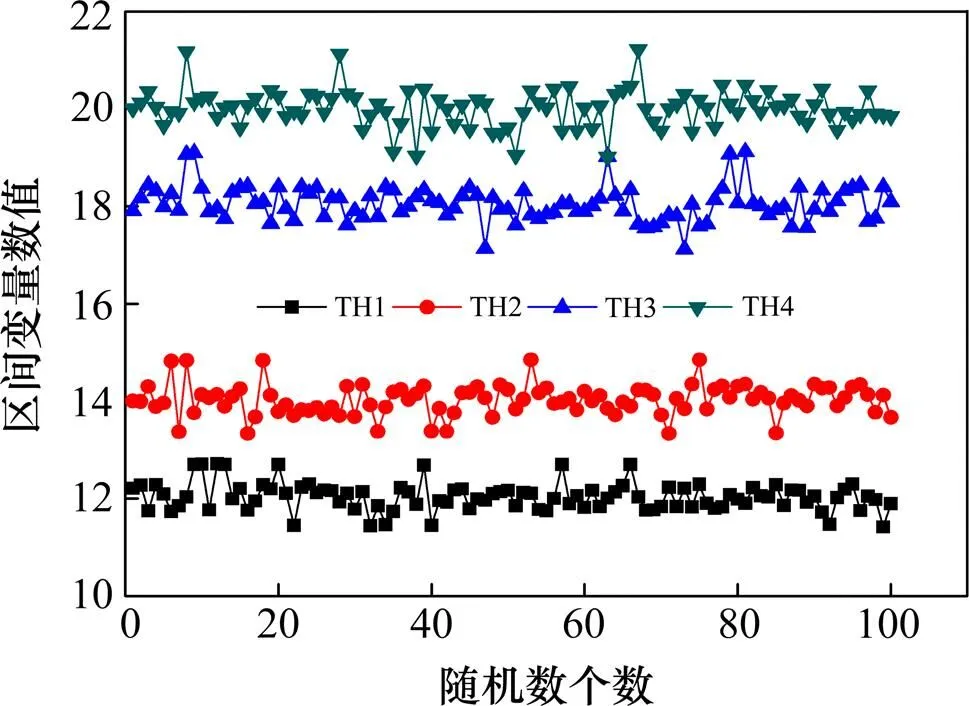
图7 分段函数区间变量

由图8可知，各个区间变量整体服从正态分布，且波动范围与表1中给定的区间范围相当接近，说明变量的取值与分段函数模型的取值范围一致，具有可比性。对比图7和图9可以看出，分段函数模型产生的区间变量的波动比均匀分布下的波动较小，更加靠近均值。图10为动车组转向架构架的结构可靠性随屈服强度变化的可靠度值。根据图10可知，当不考虑材料的不确定性，即材料屈服强度恒定时，转向架构架的结构可靠度不全为1，考虑材料的不确定性，即材料屈服强度变化时，转向架构架的结构可靠度也随之变化。反映了转向架样件的实验结果具有很大的局限性，不能准确预测整批产品是否满足静强度要求。整体来看，正态分布下的构架的可靠度值最高，其次为分段函数模型下的构架可靠度，均匀分布下的构架可靠度值最为保守。产生这种现象的原因在于分段函数考虑到工程实际中对可控因素的控制，不断提高加工水平，使其加工尽可能接近均值，克服了均匀分布下过于保守的缺陷。这也与图9中区间变量取值相符，即均匀分布的离散性比分段函数模型大。整体来看，分段函数模型与正态分布模型较为接近，但是相比正态分布偏安全，且无需大量的数据信息。

(a) TH1产生的随机数；(b) TH2产生的随机数；(c) TH3产生的随机数；(d) TH4产生的随机数

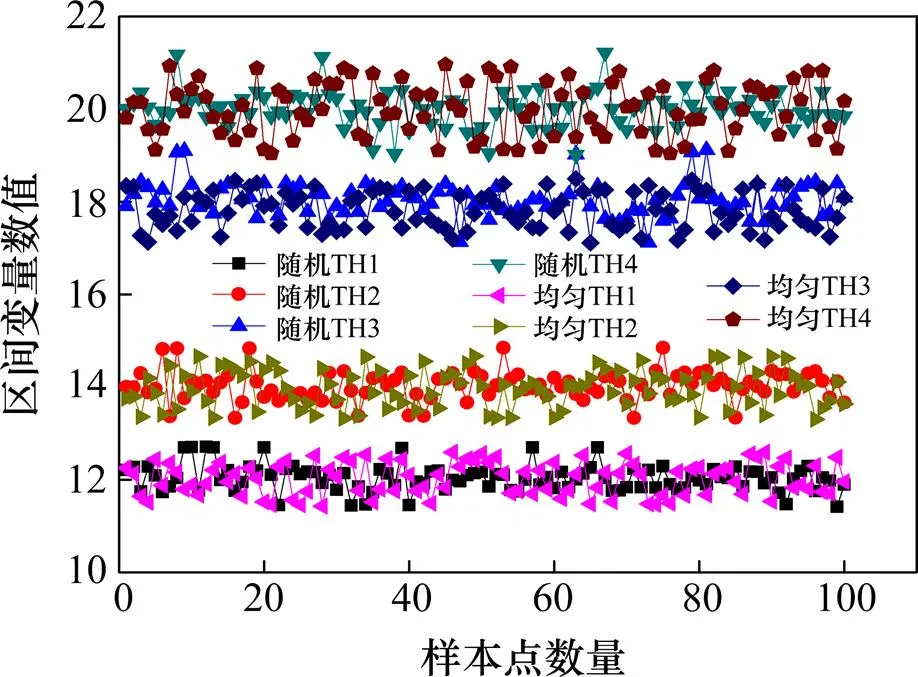
图9 区间变量均匀分布与分段函数值对比

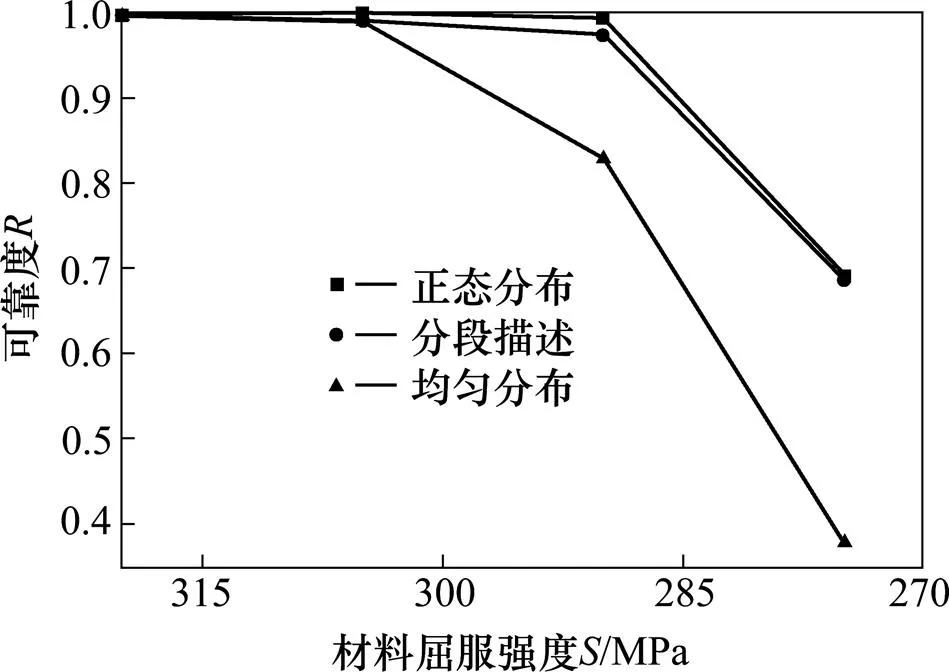
图10 可靠度对屈服强度变化曲线

6 结论

1) 该方法克服了传统区间分析中变量服从均匀分布时，计算结果较为保守的缺陷，相比概率可靠性而言，无需获得变量的统计分布特征。对于数据缺乏的复杂机械结构的可靠性设计具有一定的指导意义。

2) 转向架构架结构可靠性分析结果表明，基于6的非概率可靠性计算方法，更加趋近概率可靠性计算，且偏于安全，计算结果更有说服力。

3) 通过在计算中考虑构架结构尺寸的不确定性和实验过程中施加载荷的随机性，解决了转向架构架由于实验成本高难以获取大量测试数据造成的无法准确评估整批产品结构可靠性的问题。

[1] 卢耀辉, 曾京, 邬平波, 等. 铁道车辆转向架构架可靠性参数灵敏度分析[J]. 中国铁道科学, 2010, 31(1): 111−115. LU Yaohui, ZENG Jing, WU Pingbo, et al. Parametric sensitivity analysis for the bogie frame reliability of railway vehicle[J]. China Railway Science, 2010, 31(1): 111−115.

[2] Elishakoff I. Essay on uncertainties in elastic and viscoelastic structures: from a. m. freudenthal’s criticisms to modern convex modeling[J]. Computers & Structures, 1995, 56(6): 871−895.

[3] 祁武超, 邱志平. 基于区间分析的结构非概率可靠性优化设计[J]. 中国科学: 物理学力学天文学, 2013, 43(1): 85−93. QI Wuchao, QIU Zhiping. Non-probabilistic reliability- based structural design optimization based on the interval analysis method[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2013, 43(1): 85−93.

[4] 胡志鹏, 蒋占四, 高兵兵, 等. 机床主轴非概率可靠性模型的区间分析方法[J]. 机械科学与技术, 2014, 33(12): 834−1837. HU Zhipeng, JIANG Zhansi, GAO Bingbing, et al. An interval analysis method of non-probabilistic reliability model for machine tool spindle[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(12): 1834−1837.

[5] 郭书祥, 吕震宙, 冯元生. 基于区间分析的结构非概率可靠性模型[J]. 计算力学学报, 2001, 18(1): 56−60. GUO Shuxiang, LÜ Zhenzhou, FENG Yuansheng. A non-probabilistic model of structural reliability based on interval analysis[J]. Chinese Journal of Computational Mechanics, 2001, 18(1): 56−60.

[6] Ben-haim Y. Convex models of uncertainty in radial pulse buckling of shells[J]. Journal of Applied Mechanics, 1993, 60(3): 683−688.

[7] Elishakoff I, Elisseeff P, Glegg S, et al. Non-probabilistic convex-theoretic modeling of scatter in material properties[J]. AIAA Journal, 1994, 32: 843−849.

[8] 郭书祥, 吕震宙. 基于非概率模型的结构稳健可靠性设计方法[J]. 航空学报, 2001, 22(5): 451−453. GUO Shuxiang, LÜ Zhenzhou. Procedure for the robust reliability design of structures[J]. Acta Aeronautica ET Astronautica Sinica, 2001, 22(5): 451−453.

[9] 吕震宙, 冯蕴雯, 岳珠峰. 改进的区间截断法及基于区间分析的非概率可靠性分析方法[J]. 计算力学学报, 2002, 19(3): 260−264. LÜ Zhenzhou, FENG Yunwen, YUE Zhufeng. A advanced interval-truncation approach and non- probabilistic reliability analysis based on interval analysis[J]. Chinese Journal of Computational Mechanics, 2002, 19(3): 260−264.

[10] 邱志平, 胡永明. 椭球凸模型非概率可靠性度量和区间安全系数的关系[J]. 计算力学学报, 2016, 33(4): 522−527. QIU Zhiping, HU Yongming. The relations of non-probabilistic reliability measures based on ellipsoidal convex model and interval safety factors[J]. Chinese Journal of Computational Mechanics, 2016, 33(4): 522− 527.

[11] DU X. Reliability-based design optimization with dependent interval variables[J]. International Journal for Numerical Methods in Engineering, 2012, 91(2): 218− 228.

[12] 王晨, 陈清, 罗世辉, 等. 不同轮径转向架对车辆动力学性能影响分析[J]. 铁道学报, 2017, 39(1): 41−47. WANG Chen, CHEN Qing, LUO Shihui, et al. Influence of bodes with different wheel diameters on the vehicle dynamics performance[J]. Journal of the China Railway Society, 2017, 39(1): 41−47.

[13] 李万莉, 严俊, 朱福民,等. 新型轨道运料车转向架构架结构分析[J]. 中国工程机械学报, 2014, 12(4): 336− 341. LI Wanli, YAN Jun, ZHU Fumin, et al. Structural analysis on bogie frame for new rail vehicle[J]. Chinese Journal of Construction Machinery, 2014, 12(4): 336−341.

[14] 王洪娇, 杨翊仁. 地铁车辆转向架构架静强度分析的一般方法研究[J]. 城市轨道交通研究, 2016, 19(11): 43−45. WANG Hongjiao, YANG Yiren. Conventional approach to the static strength analysis of metro vehicle bogie frame[J]. Urban Mass Transit, 2016, 19(11): 43−45.

[15] 李金城, 李芾, 杨阳. 70%低地板有轨电车动力转向架构架强度分析[J]. 机车电传动, 2016(3): 87−91. LI Jinchen, LI Fu, YANG Yang. Strength analysis for 70% low-floor tram car motor bogie frame[J]. Electric Drive for Locomotives, 2016(3): 87−91.

[16] Angin D, Tiryaki A. Application of response surface methodology and artificial neural network on pyrolysis of safflower seed press cake[J]. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 2016, 38(8): 1055−1061.

[17] WU J, ZHANG Y, CHEN L, et al. A chebyshev interval method for nonlinear dynamic systems under uncertainty[J]. Applied Mathematical Modelling, 2013, 37(6): 4578−4591.

[18] LI Y, HU M, WANG F. Fatigue life analysis based on six sigma robust optimization for pantograph collector head support[J]. Advances in Mechanical Engineering, 2016, 8(11): 1−9.

Non-probabilistic reliability analysis based on six sigma of MEU bogie frame

ZHI Pengpeng1, CHEN Bingzhi2, LI Yonghua2, SONG Xueping1

(1. School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116028, China; 2. School of Locomotive and Rolling Stock Engineering, Dalian Jiaotong University, Dalian 116028, China)

Aiming at the problem that the static strength test results of the bogie frame are effective only for the test piece, and can't accurately reflect whether the structural strength of the entire batch of structures meets the requirements, a non-probabilistic reliability analysis method based on 6 Sigma was proposed. Firstly, the structural strength analysis of the bogie frame was made to determine the interval variable of larger force of the part, and the D-optimal test design was carried out on the basis of the parameterized model and the polynomial response surface function was established to characterize the bogie frame structure characteristics. Secondly, combining the 6 Sigma principle and the Chebyshev inequality, a piecewise function model describing interval variables was established, and the generation strategy of inter area variables and the calculation method of non-probabilistic reliability were given. Finally, taking the EMU bogie frame as the research object, the structural reliability analysis was carried out and compared with the traditional analysis method. The results show that under the condition of lack of information or small sample, the piecewise function model reflects the structural reliability of the whole batch structure better and makes up for the relatively conservative defects based on the assumption of uniform distribution. At the same time, it solved the limitations of the experimental results caused by fewer testing times.

bogie frame; non-probabilistic reliability; D-optimal design; six sigma principle; Chebyshev inequality

10.19713/j.cnki.43−1423/u.2019.02.026

U271.91

A

1672 − 7029(2019)02 − 0478 − 09

2018−02−13

国家自然科学基金资助项目(51875073，51605069)；国家重点研发计划资助项目(2016YFB1200504)；辽宁省自然科学基金资助项目(20170540112)

李永华(1971−)，女，黑龙江青冈人，教授，博士，从事轨道车辆现代化设计方法，机械产品数字仿真与优化设计、质量与RAMS工程研究；E−mail：yonghuali@163.com

(编辑 阳丽霞)