钢筋沥青隔震层弹性极限状态方程研究

尚守平，宋炼



钢筋沥青隔震层弹性极限状态方程研究

尚守平，宋炼

(湖南大学 土木工程学院，湖南 长沙 410082)

基于钢筋沥青隔震层的基本构造和工作原理，将钢筋沥青隔震层在地震作用下的竖向受力钢筋简化为上端有水平力作用下的理想轴心压杆模型，依据钢筋平面内稳定推导出钢筋沥青隔震层的弹性临界承载力与弹性极限位移公式，从而得到隔震层减震系数公式。通过单质点钢筋隔震层模型、钢筋沥青隔震层模型振动台试验验证，结果表明理论和试验符合较好。根据减震系数应用弹性临界承载力与弹性极限位移公式，能得到钢筋沥青隔震层的所有设计参数，可供设计参考和使用。

钢筋沥青隔震层；理想轴心压杆；弹性临界承载力；弹性极限位移；减震系数；振动台试验

隔震结构一般是通过引入层间刚度较小的隔震层来“阻隔”地震波向上部结构传播，从而达到减小上部结构地震响应的目的[1−5]。近年来，我国灾害性地震多发于广大村镇地区，由于长期以来农村房屋抗震意识不足，经常发生“小震大灾”现 象[6−7]。基于此，湖南大学尚守平团队针对低矮砌体结构房屋提出的一种造价低廉、施工简便、隔震性能优良的钢筋沥青隔震层[8−10]。在以往研究中，一般将隔震层的竖向钢筋简化为两端固支的梁模型，对于竖向钢筋的稳定问题没有考虑水平力作用对临界承载力的影响[9]。隔震层弹性极限位移研究主要采用数据模拟，而非理论推导[11]。针对以上问题，将钢筋沥青隔震层竖向钢筋模型简化成更接近实际情况的一端固定、一端定向滑动的梁模型，并对钢筋沥青隔震层竖向钢筋考虑地震水平力作用下进行理想轴心压杆稳定问题推导。根据以上计算模型改进后对钢筋沥青隔震层竖向钢筋的设计方法进行研究，得到更精确的理论公式。并采用振动台试验进行验证，能为钢筋沥青隔震层的设计提供设计参考。

1 钢筋沥青隔震层

位于上部结构与基础之间，由下圈梁、上圈梁，锚固于上下圈梁之间的砖墙、竖向钢筋、以及改性沥青油膏组成，隔震层构造如图1所示。竖向钢筋为主要受力构件，承受竖向荷载和水平地震作用。由于竖向钢筋的水平刚度较小，延长了隔震结构的自振周期，减小了上部结构的动力响应，从而减轻建筑震害。在多遇地震下，砖墩与上圈梁不直接接触，砖墩不承受上部结构荷载，钢筋处于弹性阶段；罕遇地震作用下由于结构位移较大，竖向钢筋倾斜，钢筋进入弹塑性，上圈梁会落在砖墩上，砖墩与竖向钢筋共同承受上部结构荷载，与一般构件恢复力模型中的刚度退化现象不同，钢筋沥青隔震层在大变形下由砖墩从不参与到参与受力导致隔震体系出现水平刚度随变形的增大而增大的情况，因此保护了上部结构不倒塌，增加了隔震体系的可靠度。以上可得，钢筋沥青隔震层能满足“小震不坏中震可修大震不倒”的三水准设计要求。此外，沥青油膏有防锈、起增大隔震阻尼，耗散地震能量的作用。

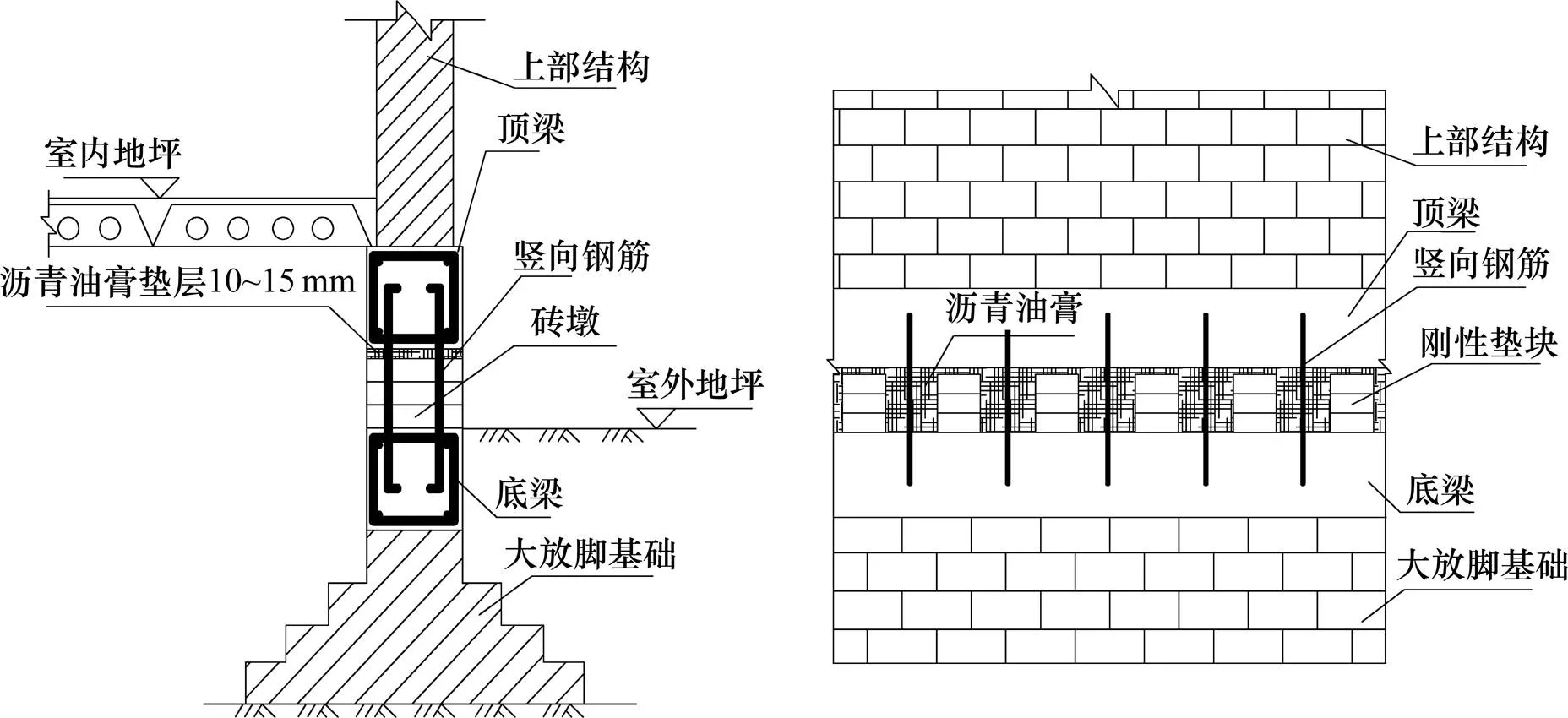
图1 钢筋沥青隔震层构造示意图

2 弹性临界承载力及弹性极限位移

2.1 计算模型

当钢筋沥青隔震层在多遇地震下，位移较小时，砖墩不承受竖向荷载，竖向钢筋为主要的受力构件，因此把竖向钢筋作为首要的研究对象。根据实际受力情况，将竖向钢筋等效成一端固定、一端为定向滑动支座的梁进行分析，其受力形式简化如图2所示。当结构承受地震作用时，要求隔震层主要靠竖向钢筋提供竖向重力荷载承载能力，同时竖向钢筋水平刚度较小，以降低上部结构水平运动加速度，达到隔震减震的目的，在多遇地震下进行隔震层设计时，为了简化计算可不考虑砖墩竖向承载力、沥青油膏的阻尼对竖向钢筋水平刚度的影响。

2.2 隔震层弹性临界承载力和弹性极限位移计算

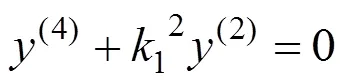
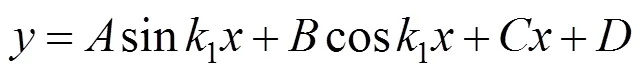
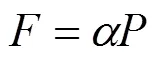
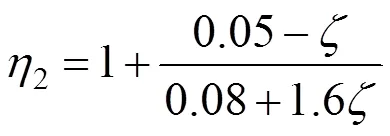
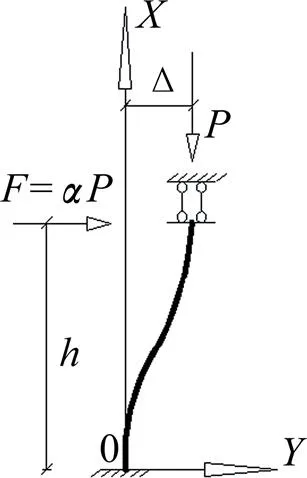
图2 钢筋受力等效结构图

引进边界条件如下：

杆端固定端的边界条件为：当=0时，位移和转角都为0，剪力为，即：

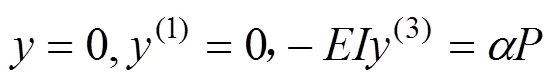
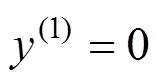
将式(1)代入上述边界条件，可得到4个线性方程，方程有4个积分常数和一个系数，为超越方程，需要补充边界条件。另一方面考虑，首先假设=0，钢筋在水平力=作用下产生变形Δ0。钢筋在初始变形Δ0时，变形图如图4所示，钢筋上下转角为0，弯矩0=0∙，其中=/为钢筋的线刚度，此时钢筋在转角0下产生附加变形Δ1。钢筋在初始变形Δ1时，钢筋上下转角为1，弯矩0=0∙，此时钢筋在转角1下产生附加变形Δ2。以此类推，钢筋的总变形为

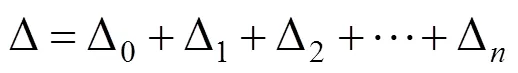
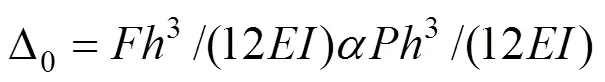
2) 依据变形图3，Δ0较小，有

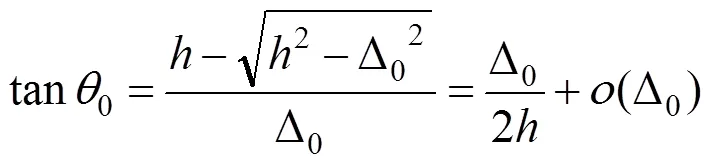
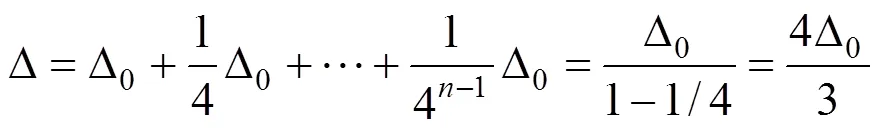
因此补充边界条件：

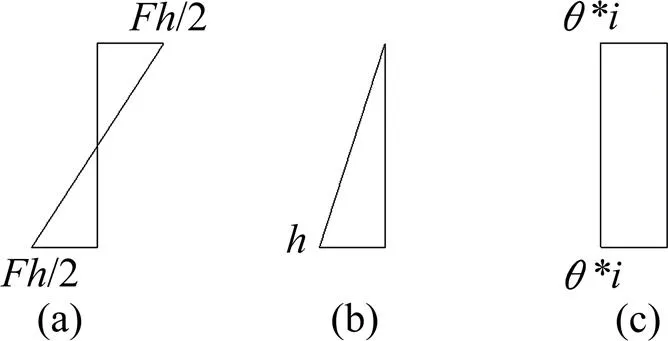
图3 弯矩图

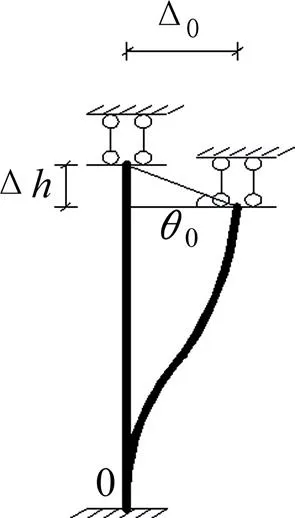
图4 Δ0作用下钢筋变形图

联立上述5个边界条件，得到方程组如下：

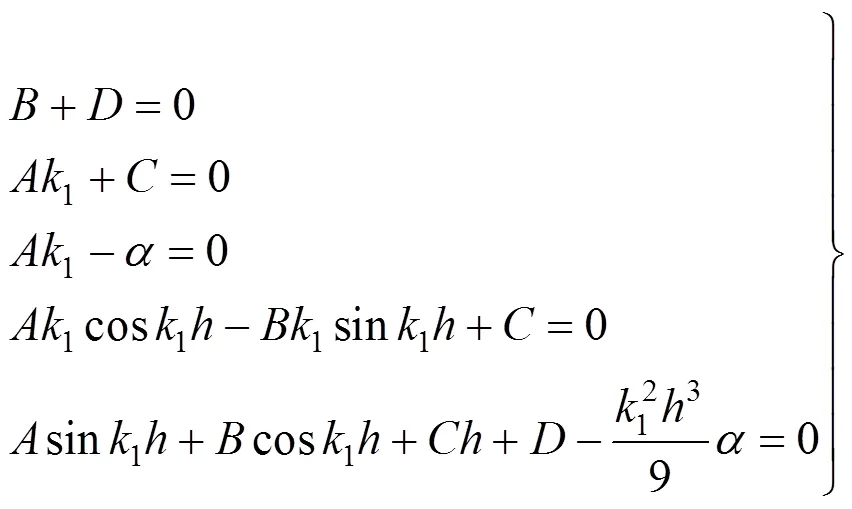
，，，和不同时为0，上式有非零解的 条件：

得到超越方程为

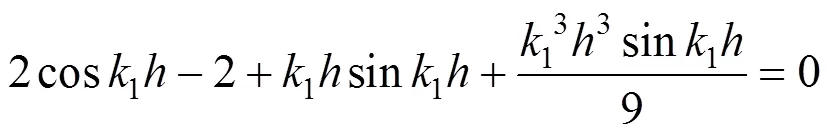
弹性极限位移为：

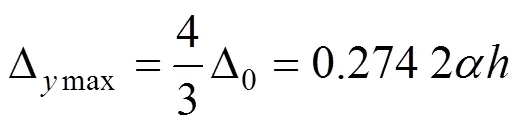
由以上可知支座处最大弯矩为：

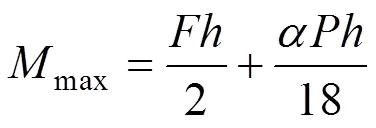
此时，支座端部截面边缘纤维应力：

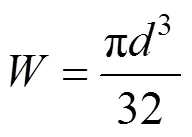
式中：为重力荷载分项系数，取1.2；为水平地震作用分项系数，取1.0(发生地震作用时产生的偶然荷载)；max为水平地震影响系数最大值；为截面抵抗矩；为竖向钢筋截面面积；,为钢筋的高度和直径。求解式(4)得临界应力

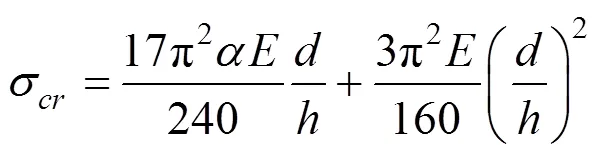
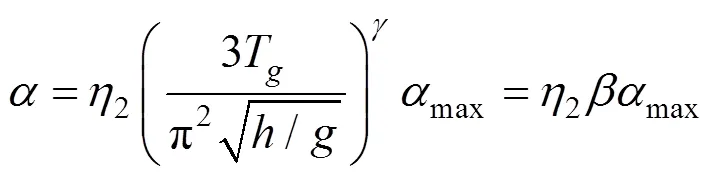
3 试验验证

为验证式(3)，(5)和(6)，采用钢筋沥青隔震层模型进行振动台试验，结合文献[10]振动台试验对不同水平地震作用下的钢筋应力、位移和减震系数进行研究。

3.1 试件模型

试验采用C30混凝土质量块，重1.25 t。采用416，高度为500 mm的光圆钢筋，长、宽、高分别为400 mm，400 mm，50 mm的2块钢板，在钢板内开槽将钢筋焊接在钢板内，组成一个钢筋隔震层。同时上下钢板分别通过螺杆与质量块、振动台固定，因此隔震竖向钢筋上端为定向滑动支座，下端为固支，振动台试验模型如图5所示；试验装置、试件及配重块如试验装配图6所示。

3.2 试验方案

3.2.1 试验材料参数

因研究对象为竖向受力钢筋，为得到钢筋的基本参数，选用同一批次的钢筋在万能试验机上进行材性试验，得出钢筋弹性模量、屈服强度如表1所示。由表1可得钢筋的屈服强度平均为367 MPa，钢筋平均弹性模量为205 GPa，则钢筋的屈服应变

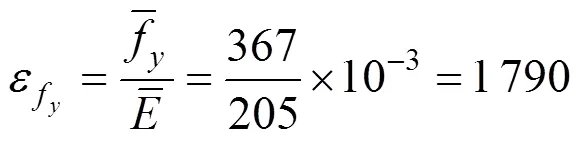
3.2.2 测量方案

试验采用振动台输入0.05，0.1和0.2，第Ⅱ类场地设计，设计地震分组分为两组。试验选用发生于1952年的Taft波和1979年的El-Centro波。试验过程中加速度采用拾振器测量，在振动台台面和质量块顶部分别布置工程力学研究所生产的941B拾振器，拾振器布置见图7。钢筋应变采用动态应变采集仪量测，选取对角线的2根钢筋，在钢筋顶部和底部对称位置分别布置2个应变片，一共8个应变片，以钢筋的应变大小判断钢筋的弹塑性状态。

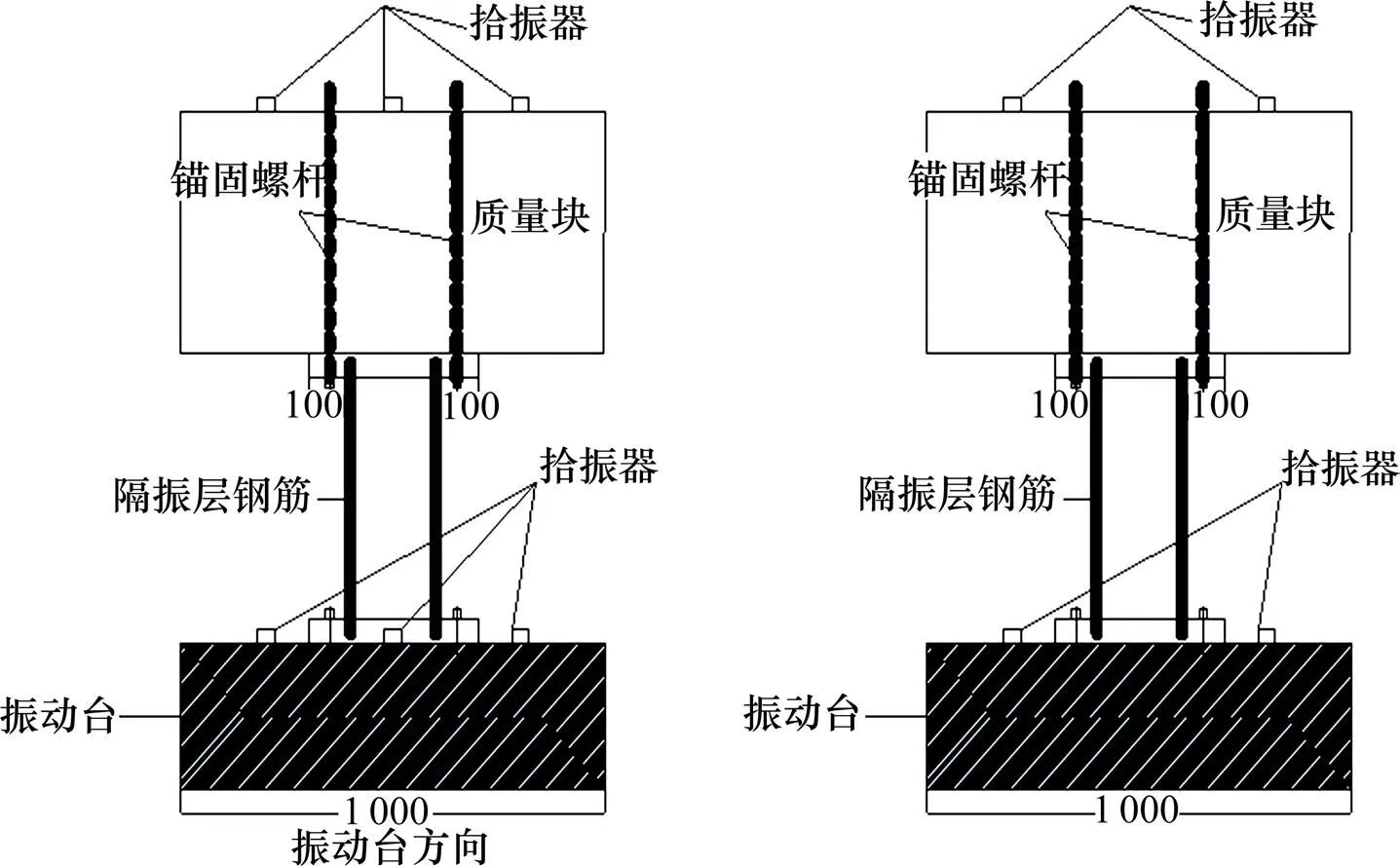
图5 振动台试验模型示意图

图6 试验装配图

表1 钢筋材性参数

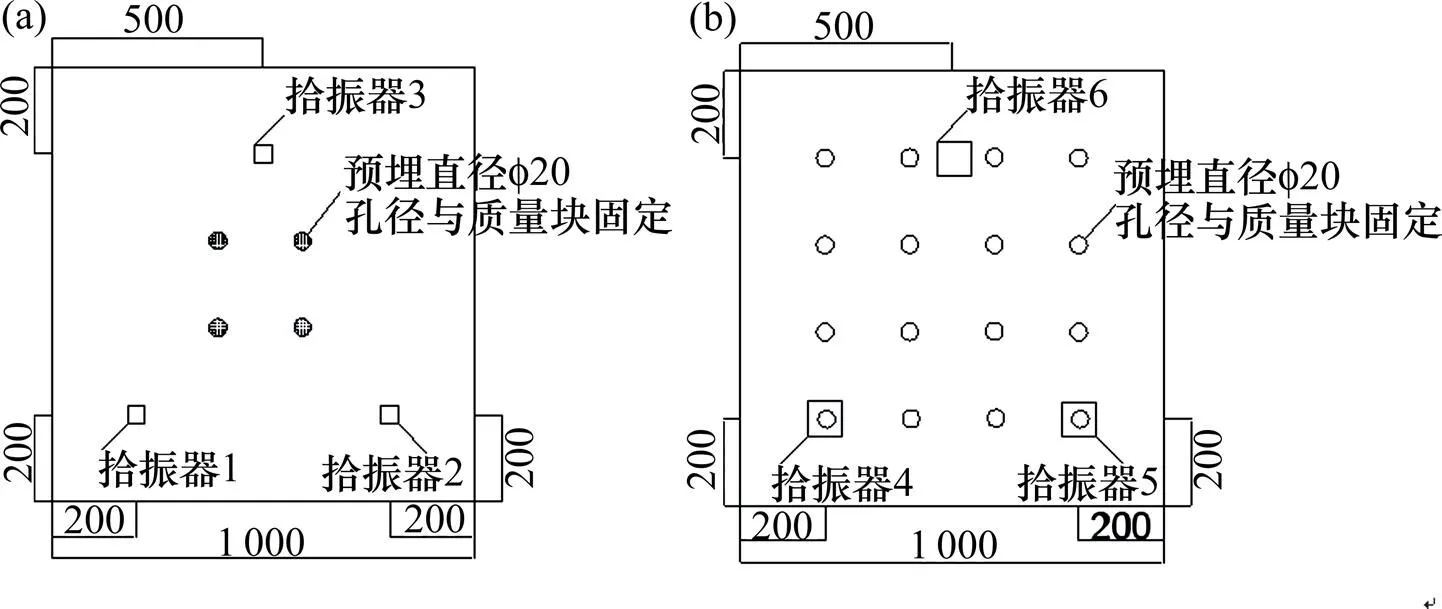
(a) 质量块平面；(b) 振动台台面平面

3.2.3 试验结果

试验在湖南大学结构防灾减灾实验室采用低频激振器二次开发制作的振动台上进行。试验时，台面加载加速度为0.05，0.1和0.2，测点3和测点6分别采集了振动台台面和质量块的位移。测点1和2采集振动台加速度，测点4和5采集质量块加速度，动态应变仪记录震动过程中的钢筋应变。绝对最大相对位移值、绝对最大钢筋应变及弹性极限位移如表2所示。由参考文献[10]可知，当台面加速度为0.1时，通过计算可知应变在弹性范围，此时隔震层钢筋处于弹性状态；当台面加速度为0.2时，隔震层产生大位移，钢筋进入弹塑性阶段，选取文献[10]在工况0.1和0.2时的数据如表3所示。

3.3 试验验证

3.3.1 强度验证

由表2得，台面加速度为0.1时，弹性模量=205 GPa、屈服强度为367 MPa和最大地震影响系数为0.05，代入式(5)得钢筋压应力为268.1 MPa＜367 MPa。台面加速度为0.2时，最大地震影响系数为0.1，代入式(5)得钢筋压应力为497.4 MPa＞367 MPa。

由表3，当台面加速度为0.1，弹性模量为=200 GPa，最大地震影响系数为0.056，代入式(5)，可得杆件压应力为 268.2 MPa＜367 MPa。

文献[10]中，当台面加速度为0.2，最大地震影响系数为0.112，代入式(5)，得杆件压应力为503.1 MPa＞367 MPa。

经计算，验证了式(5)是正确的。

3.3.2 稳定验证

由3.2.1可知，本次和参考文献[10]的振动台试验中：台面加速度为0.1时，竖向钢筋处于弹性阶段；台面加速度为0.2时，竖向钢筋已进入弹塑性。由表2和表3得，0.1工况下，为弹性位移，0.2工况下为弹塑性位移，采用式(3)计算的弹性极限位移大于工况0.1、小于工况0.2的试验实测位移，验证了式(3)是正确的。

3.3.3 减震系数验证

由表3可得，减震系数为

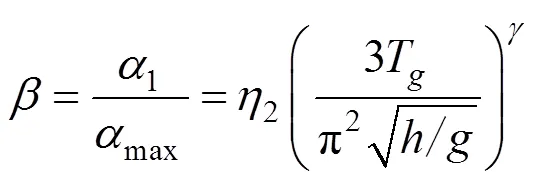
通过以上3个方面验证，式(3)，(5)和(6)作为钢筋沥青隔震层的弹性极限位移、临界应力和减震系数是正确的。

3.4 公式应用推广

在隔震结构中，减震系数太小，会影响隔震结构的正常使用，当减震系数太大，隔震效果不明显，因此减震系数一般取0.4~0.6之间。当减震系数给定以后，由抗震设防烈度、场地特征和结构阻尼比结合式(6)可得钢筋高度，定好钢筋强度和型号后由(5)可知。因此在设计过程中，可以依据抗震设防烈度、目标减震效果，实现钢筋直径、高度、根数之间的便捷组合。

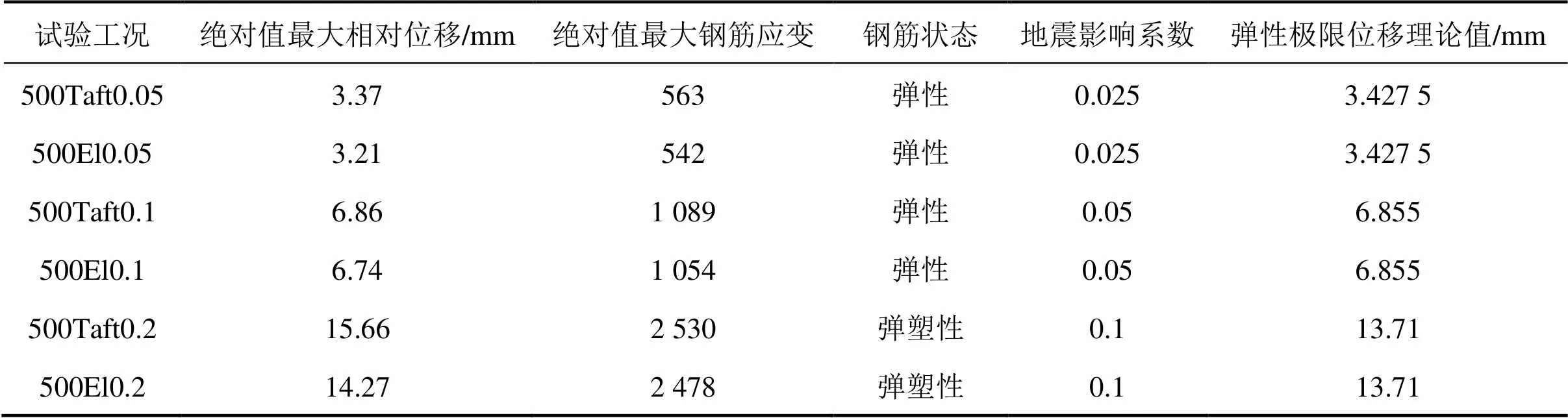
表2 绝对最大相对位移值、绝对最大钢筋应变值及弹性极限位移

注：1) 以工况代号500Taft0.05为例，500表示钢筋高度为500 mm，El表示输入波形为El-Centro0.05表示台面输入最大加速度为0.1，以此类推；2) 绝对值最大相对位移为台面输入位移与隔震层输出位移之差中绝对值最大的位移

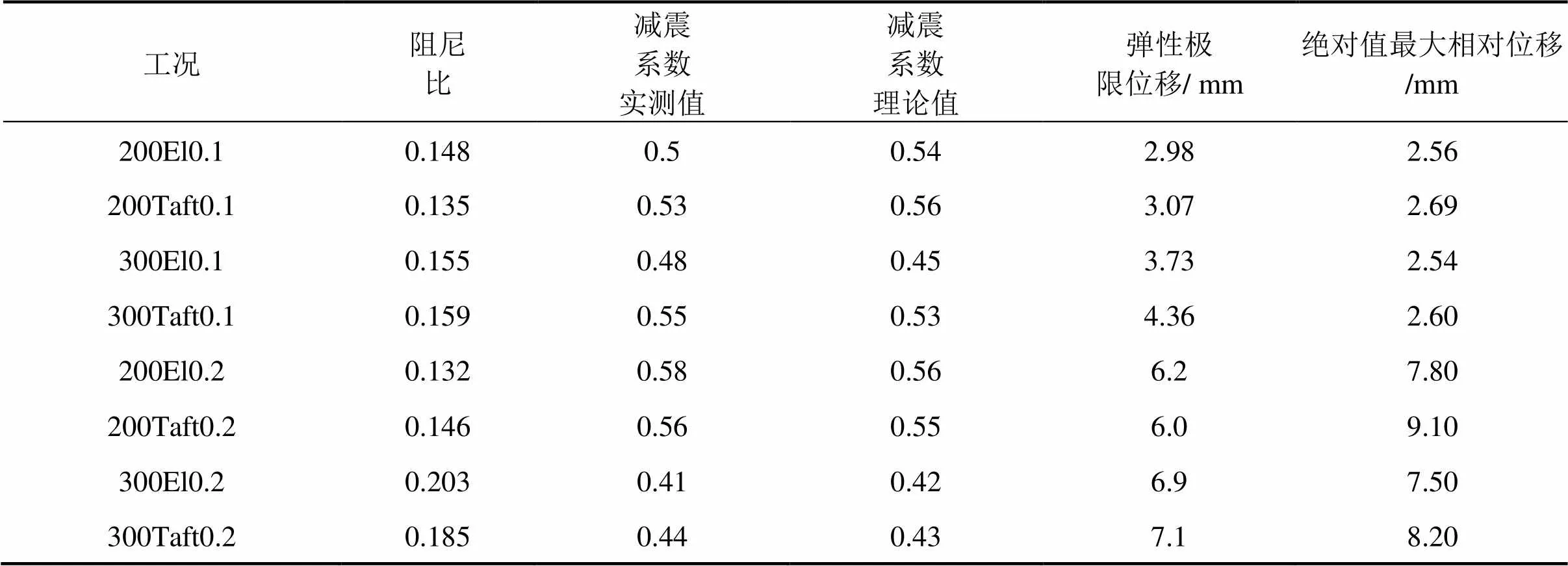
表3 参考文献[10]试验数据

4 结论

1) 基于理论推导和试验验证，钢筋沥青隔震层弹性临界承载力和弹性极限位移能采用式(3)和(5)。

2) 钢筋沥青隔震层竖向钢筋弹性极限位移公式采用理论推导，结果可靠。应用振动台试验验证，试验结果和理论公式符合的较好。最后应用推导公式，能根据减震效果进行隔震层参数设计，即隔震层钢筋高度、直径、屈服强度和根数的组合，从而较大提高了钢筋沥青隔震层的设计灵活性和可操作性。

3) 虽然式(6)是基于弹性范围考虑的，但可以根据减震系数在0.4~0.6之间给出钢筋高度和直径的适用范围。

[1] PAN Peng, YE Lieping, SHI Wei, et al. Engineering practice of seismic isolation and energy dissipation structures in China[J]. Science China (Technological Sciences), 2012, 55(11): 3036−3046.

[2] 尚守平, 崔向龙. 基础隔震研究与应用的新进展及问题[J]. 广西大学学报(自然科学版), 2016, 41(1): 21−28. SHANG Shouping, CUI Xianglong. New progress and problems in research and application of base isolation[J]. Journal of Guangxi University (Natural Science Edition), 2016, 41(1): 21−28.

[3] Karayel V, Yuksel E, Gokce T, et al. Spring tube braces for seismic isolation of buildings[J]. Earthquake Engineering and Engineering Vibration, 2017, 16(1): 219−231.

[4] MA Chao, LU Dechun, DU Xiuli. Seismic performance upgrading for underground structures by introducing sliding isolation bearings[J]. Tunnelling and Underground Space Technology, 2018, 4(74): 1−9.

[5] SHI Zhifei, CHENG Zhibao, XIANG Hongjun. Seismic isolation foundations with effective attenuation zones[J]. Soil Dynamics and Earthquake Engineering, 2014(57): 143−151.

[6] 曹万林, 戴租远, 叶炜, 等. 村镇建筑低成本隔震技术研究现状与展望[J]. 自然灾害学报, 2014, 23(6): 38−46. CAO Wanlin, DAI Zuyuan, YE Wei, et al. Research and prospect of low-cost isolation techniques for rural buildings[J]. Journal of Natural Disasters, 2014, 23(6): 38−46.

[7] 谭平, 徐凯, 王斌, 等. 基于新型简易隔震支座的村镇建筑隔震性能研究[J]. 土木工程学报, 2013, 46(5): 64−70. TAN Ping, XU Kai, WANG Bin, et al. Performance study of isolated rural buildings using novel simple isolators[J]. China Civil Engineering Journal, 2013, 46(5): 64−70.

[8] 尚守平, 周志锦, 刘可, 等. 一种钢筋−沥青复合隔震层的性能[J]. 铁道科学与工程学报, 2009, 6(3): 13−16. SHANG Shouping, ZHOU Zhijin, LIU Ke, et al. The research on the steel-asphalt isolation layer[J]. Journal of Railway Science and Engineering, 2009, 6(3): 13−16.

[9] 尚守平, 朱博闻, 吴建任, 等. 钢筋−沥青复合隔震层实际工程应用研究[J]. 湖南大学学报(自然科学版), 2013, 40(7): 1−8. SHANG Shouping, ZHU Bowen, WU Jianren, et al. Research on steel-asphalt isolation layer in practical engineering[J]. Journal of Hunan University (Natural Sciences), 2013, 40(7): 1−8.

[10] 尚守平, 姚菲, 刘可.一种新型隔震层的构造及其振动台试验研究[J]. 土木工程学报, 2011, 44(2): 36−41. SHANG Shouping, YAO Fei, LIU Ke. Study of the strucyure of a new type of isolation layer and shaking table test[J]. China Civil Engineering Journal, 2011, 44(2): 36−41.

[11] 尚守平, 杨龙. 钢筋沥青隔震层位移控制研究[J]. 土木工程学报, 2015, 48(2): 26−33. SHANG Shouping, YANG Long. Research on displacement control of steel-asphalt isolation layer[J]. China Civil Engineering Journal, 2015, 48(2): 26−33.

[12] 童根树. 钢结构的平面内稳定[M]. 北京: 中国建筑工业出版社, 2015. TONG Genshu. In-plane stability of steel structures[M]. Beijing: China Building Industry Press, 2015.

Research on stability of resilience of reinforced asphalt isolated layer

SHANG Shouping, SONG Lian

(School of Civil Engineering, Hunan University, Changsha 410082, China)

This paper introduces the basic structure and working principle of steel reinforced steel-asphalt isolated layer, and simplifies the vertical reinforcement force mode of reinforced steel asphalt isolated layer under the action of earthquake to an ideal axial compression pole model with horizontal force, and deduces the elastic critical bearing capacity and elastic limit displacement formula of reinforced asphalt isolated layer according to the stability of the steel reinforced plane so as to obtain the formula of damping coefficient of seismic isolation layer. Through the single-point reinforced-steel isolation layer model and reinforced asphalt-rock vibration isolation table model test, the results show that the theory and test are in good agreement. According to the elastic critical bearing capacity applied with damping coefficient and elastic limit displacement formula, all the design parameters of steel asphalt isolated layer can be obtained for design reference and use.

steel-asphalt isolation layer; ideal shaft compression rod; elastic critical load capacity; elastic limit displacement; shock absorption coefficient; shaking table test

10.19713/j.cnki.43−1423/u.2019.02.024

TU352

A

1672 − 7029(2019)02 − 0464 − 07

2018−01−29

国家“十二五”科技支撑计划资助项目(2015BAL03B01)

尚守平(1953−)，男，山东黄县人，教授，博士，从事工程结构抗震及加固研究；E−mail：sps@hnu.edu.cn

(编辑 蒋学东)