盾构管片接头破坏类型及参数敏感性分析

张平平，杨伟超，尹荣申，邓锷



盾构管片接头破坏类型及参数敏感性分析

张平平，杨伟超，尹荣申，邓锷

(中南大学 土木工程学院，湖南 长沙 410075)

盾构管片接头是整环管片力学性能的薄弱部位，容易发生破坏。通过分析盾构管片接头的受力特性、管片接头的破坏类型以及管片内力和其影响因素之间的关系,再进行人工神经网络敏感性分析，计算得到不同影响因素的相对重要性指数大小。研究结果表明：盾构管片接头的破坏类型为受拉破坏；管片外径(=54.4%)对管片最大拉应力影响最大，其次是围岩等级(=35.3%)，隧道埋深和混凝土强度对管片最大拉应力影响较小，相对重要性指数小于6%。

盾构管片接头；破坏类型；敏感性分析；相对重要性指数

盾构法因其快速安全的特点在城市地铁建设过程中得到了广泛的应用。管片是盾构法中重要的衬砌手段，而管片接头往往是其力学性能的薄弱和关键环节，也是整环管片最容易出现破坏的部位。管片接头发生破坏会导致管片整体刚度下降，影响衬砌结构的耐久性。因此，国内外学者就盾构管片的破坏类型及破坏过程进行了深入的研究。唐志成等[1]依托南京地铁一号线工程，通过相似模型试验对管片衬砌结构的力学行为进行分析，认为管片衬砌结构的破坏首先在拱顶或仰拱的环向接头部位出现细小纵向裂缝，随着荷载增加，在接近拱腰的环向接头外侧也出现细小裂缝，并且裂缝宽度和长度不断增加；杨雄[2]依托南京长江隧道工程，通过相似模型试验研究了水、土压力作用下管片的破坏形态特征，试验结果表明管片破坏的部位最先在拱顶和拱底产生，然后接头附近也出现裂缝，最后在水平位置偏上15°左右范围出现压溃破坏区域；毕湘利等[3]通过足尺静载试验，认为管片极限破坏特征表现为管片接头的破坏，管片本身并未表现出明显的破坏现象，且随着荷载的增加，管片接缝内弧面混凝土受压开裂。裂缝是管片发生破坏的外在特征，而管片内力超出极限承载力才是管片发生破坏的内因。影响盾构管片内力分布的因素主要包括2大类，第1类是盾构管片本身的结构及参数对其内力分布的影响[4]，第2类为盾构管片周围土体对其内力分布的影响[5]。宋锦虎等[6]通过计算得到不同间距、不同埋深、不同土体力学参数情况下管片最大内力提高率，得知埋深和土体黏聚力对提高率影响较弱，土体内摩擦角的影响较为显著。丁军霞 等[7]从土层与衬砌两方面分析了影响管片衬砌内力的各个影响因素以及管片内力随各个参数变化规律。上述研究对于管片内力与影响因素的关系进行了一定的分析，但是对于不同影响因素组合下影响因素的敏感性分析较少。本文建立盾构管片三维有限元模型，分析不同参数影响下盾构管片接头破坏类型及其内力分布特性，进而借助人工神经网络敏感性分析，得到不同参数的相对重要性大小。

1 计算模型和方法

1.1 计算模型

1.1.1 三维有限元分析模型

在ABAQUS中建立盾构管片三维有限元分析模型，盾构管片、道床和围岩采用三维实体单元模拟，单元类型以六面体为主。管片与管片、衬砌与围岩之间设置接触面，接触属性为硬接触。衬砌与道床之间采用绑定约束，衬砌结构内表面与道床下表面一起工作，没有相对位移。盾构管片模型见图1。

管片连接螺栓采用梁单元模拟，通过嵌入的方式将螺栓置入到管片混凝土单元中。管片接头模型见图2。

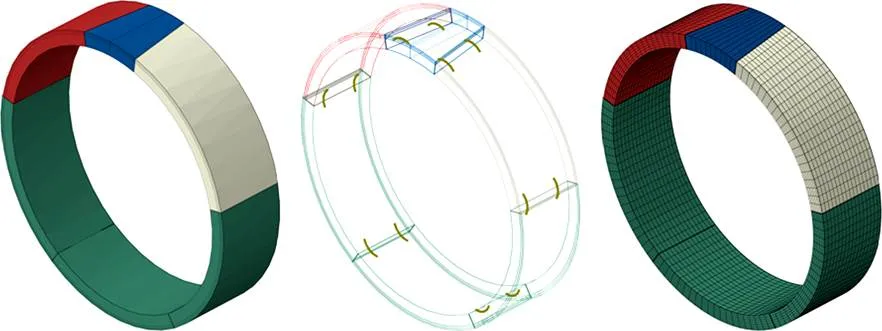
图1 盾构管片模型

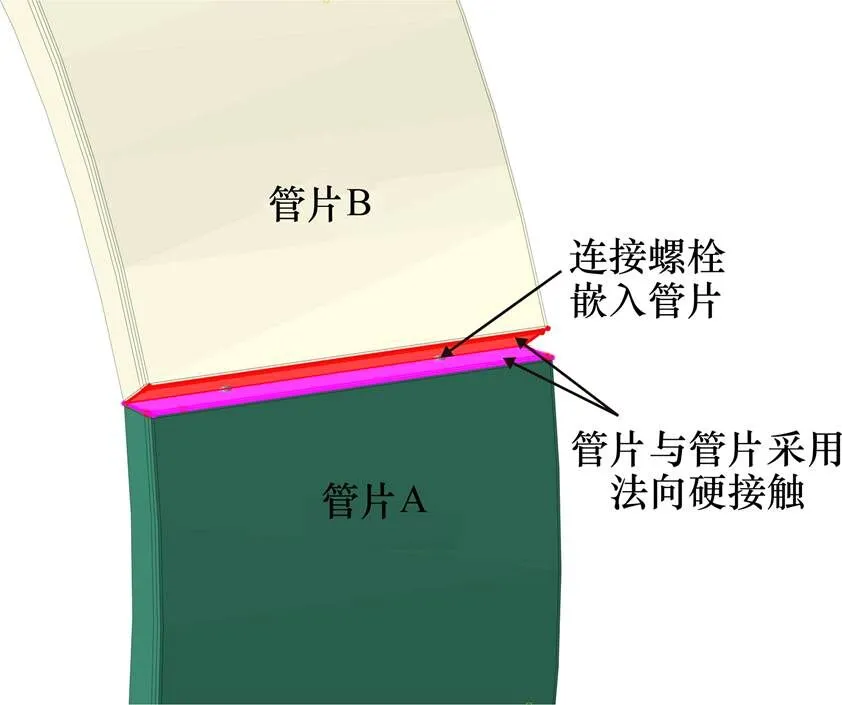
图2 管片接头模型

道床−管片−围岩的计算模型如图3所示。围岩沿隧道横向取100 m，竖向取60 m。围岩上表面设置自由约束，其他表面设置位移约束。模型初始应力场只考虑自重应力场，不计构造应力场的影响。除重力荷载以外，还要考虑地铁列车荷载对盾构管片内力的影响。参照文献[8]，取车轮静载0作为列车荷载，0=80 kN。

1.1.2 材料参数

三维有限元计算模型中，围岩与道床采用摩尔−库伦屈服准则下的弹塑性本构模型，管片与螺栓采用线弹性本构模型，基本材料参数见表1。

1.1.3 影响因素

本文仅考虑隧道埋深为浅埋的情况，建立隧道埋深分别为15，20和25 m的计算模型，分析不同埋深条件下盾构管片内力。

在盾构法施工中，围岩与盾构管片之间存在较强的相互作用[9]，在自重应力场作用下，盾构管片拱顶会出现拉应力区。因此，参照文献[10]中列出的围岩等级条件，本文选取3种等级围岩作为盾构管片内力影响因素。围岩的物理力学参数取值见表2。

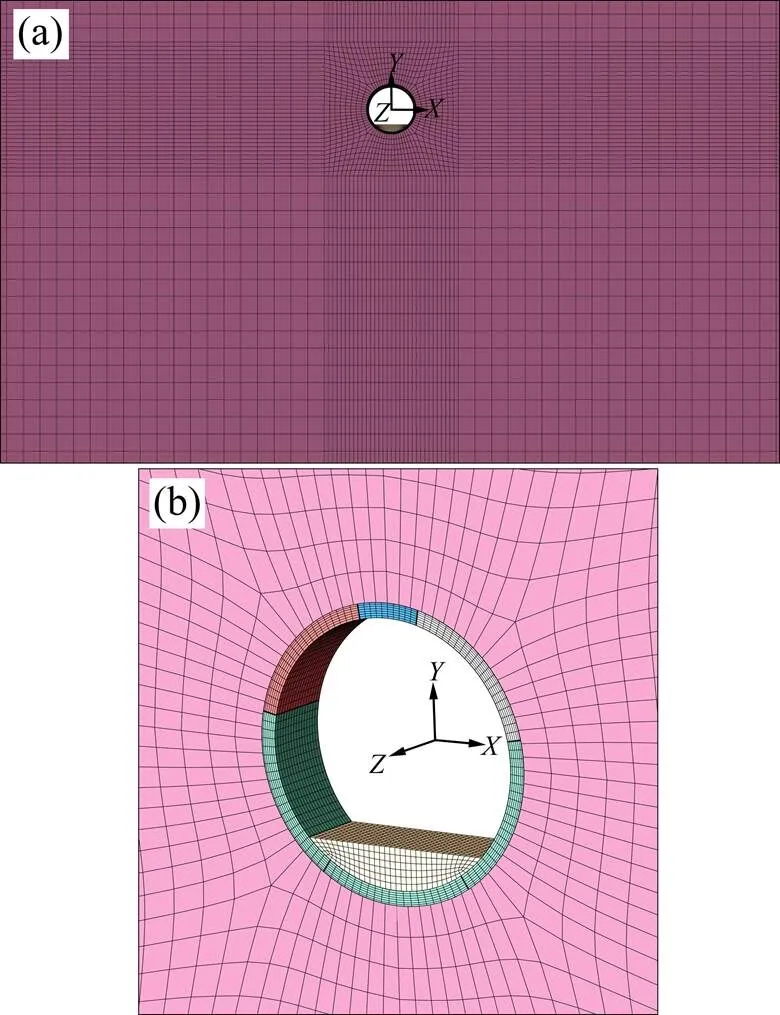
(a) 计算模型正面网格图；(b) 道床−管片−围岩网格划分

表1 材料物理力学参数

表2 围岩物理力学参数

盾构管片作为隧道主要承重载体，在盾构法中具有重要作用[10]。盾构法中，盾构管片主要分为小直径盾构管片、大直径盾构管片和超大直径盾构管片，盾构管片类型及其参数见表2。盾构法施工中管片常用的混凝土为C50和C60，本文选取C50，C55和C60 3种混凝土，分析混凝土强度对管片内力的影响。

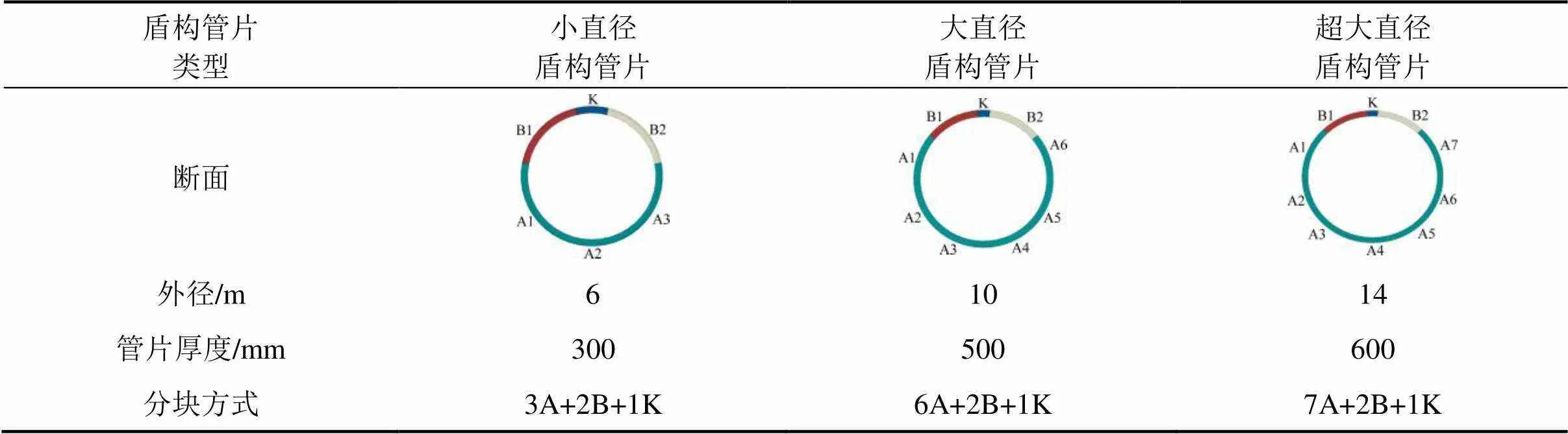
表3 盾构管片类型

综上所述，考虑隧道埋深为浅埋，计算不同围岩等级条件下，管片衬砌结构采用不同强度等级的混凝土时盾构管片内力。计算工况如表4所示。

表4 计算工况

1.2 人工神经网络敏感性分析

人工神经网络[11](Artificial neural network)是受大脑的生物学结构和功能启发的简化数学模型。人工神经网络的主要优势是可以通过分配或调整连接权重来学习，训练和使用数据。

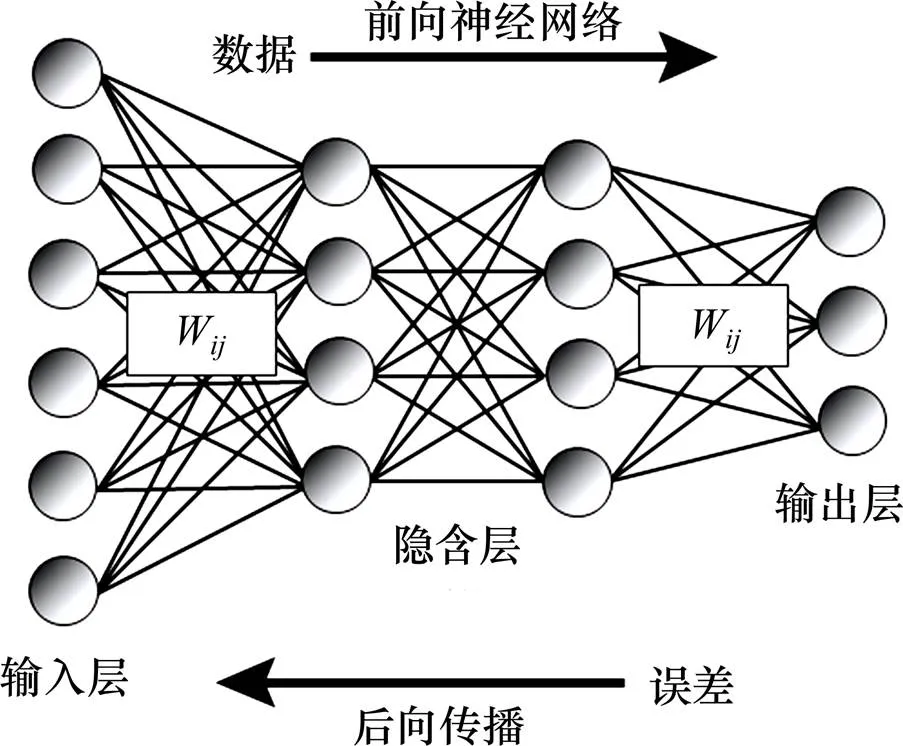
图4 人工神经网络的典型结构

人工神经网络包含3层网络：输入层、隐含层和输出层，如图4所示。数据由输入层逐层传递至输出层，输出层计算误差并逐层反向传递，然后对神经元之间的权重和阈值进行调整，使得神经网络趋稳定，误差接近目标值，从而完成对网络的训练。

通过选取适当的数据进行训练，人工神经网络可以清楚地描述输入层变量和输出层结果之间的关系。此外，神经网络也可以通过敏感性分析来识别哪些输入变量对输出结果有更大的影响。

2 分析结果

2.1 盾构管片内力分布特性及破坏类型

图5~6为大直径盾构管片在隧道埋深15 m处，围岩等级为Ⅳ级条件下，管片使用C50强度等级的混凝土时盾构管片应力分布。

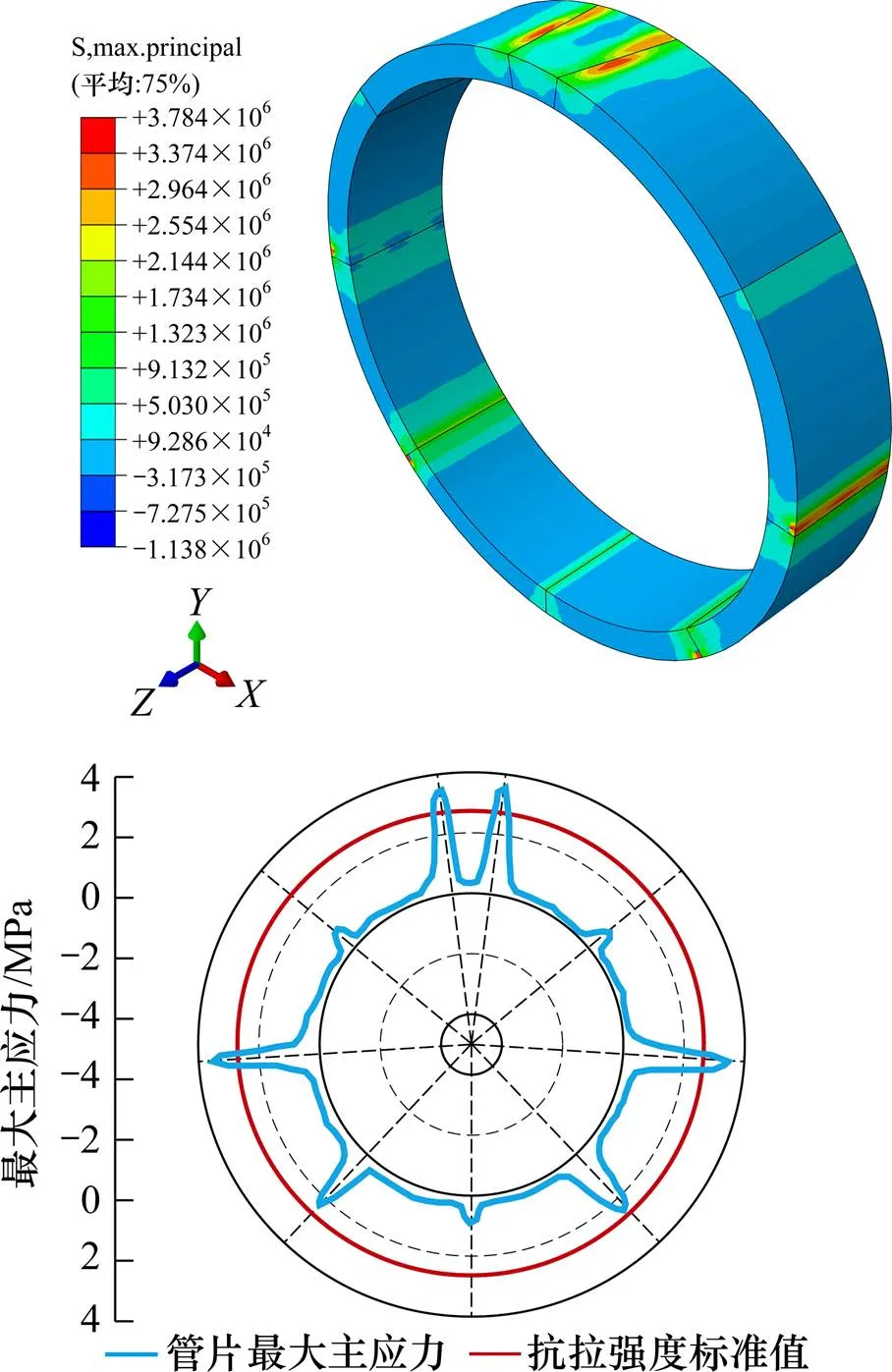
图5 盾构管片拉应力

由图5可得，盾构管片接头呈现明显的应力集中，管片接头处的拉应力明显大于其他位置的拉应力。盾构管片拉应力大致呈现出轴对称分布，拱顶和拱腰接头处的拉应力大于混凝土极限抗拉强度，管片接头会发生受拉破坏，混凝土出现开裂。管片出现裂缝的位置与文献[1]中试验得到的位置相吻合，进一步说明了盾构管片的拱顶和拱腰处是整环管片最容易出现破坏的位置。

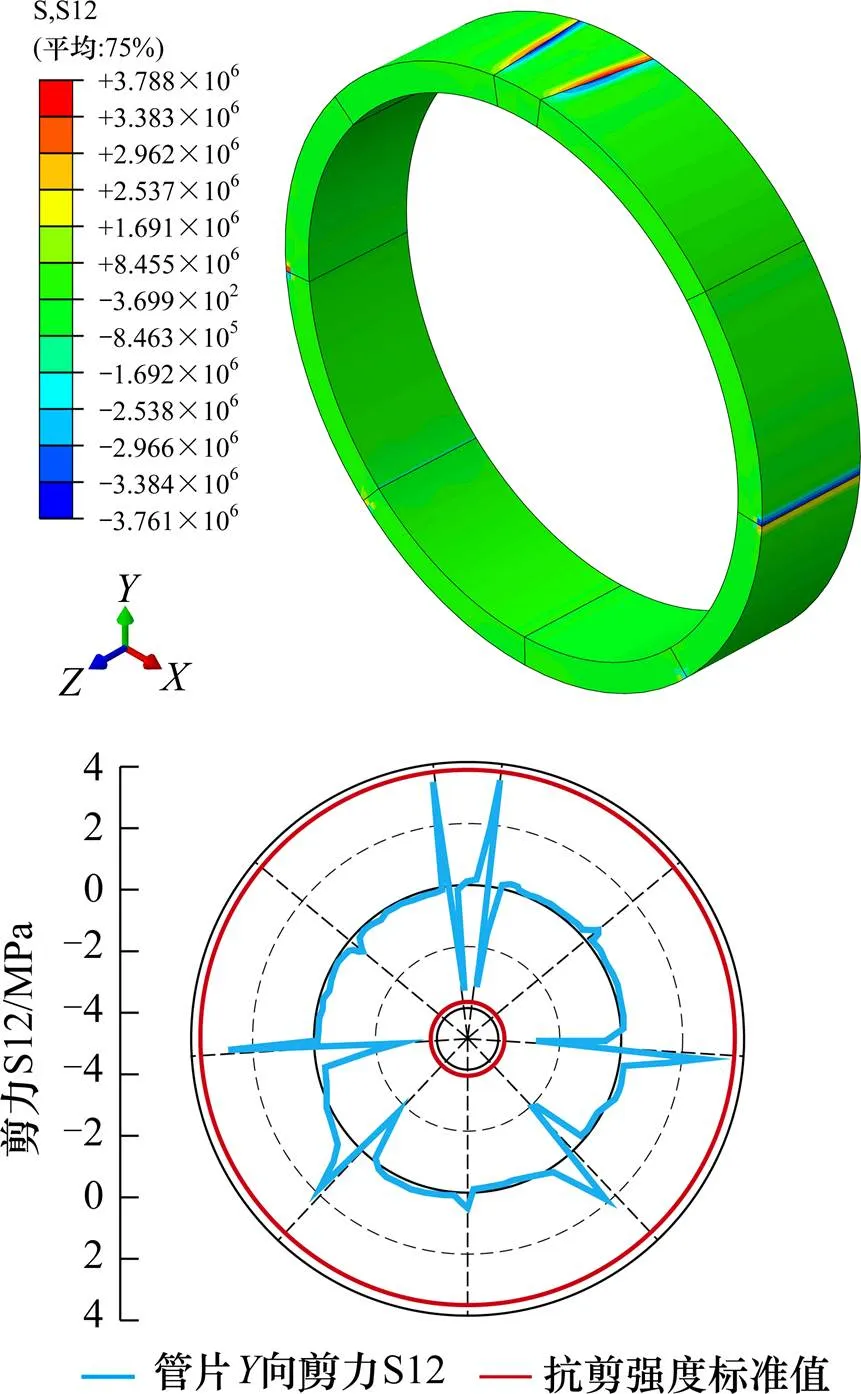
图6 盾构管片剪应力

盾构管片的剪应力沿，和轴分为3个方向的分力，分别为S12，S13和S23，其中沿轴的分力S12最大，剪应力S12如图6所示。盾构管片接头的剪应力同样明显大于其他位置的剪应力，管片接头呈现明显的应力集中。盾构管片剪应力S12大致沿轴反对称分布，拱顶和拱腰接头处的剪应力小于混凝土抗剪强度标准值，管片不会发生剪切破坏。

综上，盾构管片接头呈现明显的应力集中，拱顶和拱腰处管片接头拉应力大于混凝土抗拉强度，剪应力小于混凝土抗剪强度，管片接头的破坏类型为受拉破坏。

2.2 不同因素下盾构管片拉应力的变化规律

图7为盾构管片拉应力与隧道埋深、管片外径、围岩等级和混凝土强度之间的关系。图7(a)为围岩等级Ⅳ级，混凝土强度C50条件下盾构管片拉应力与隧道埋深的关系；图7(b)为隧道埋深15 m，混凝土强度C50条件下盾构管片拉应力与围岩等级的关系；图7(c)为隧道埋深15 m，围岩等级Ⅳ级条件下盾构管片拉应力与混凝土强度的关系。

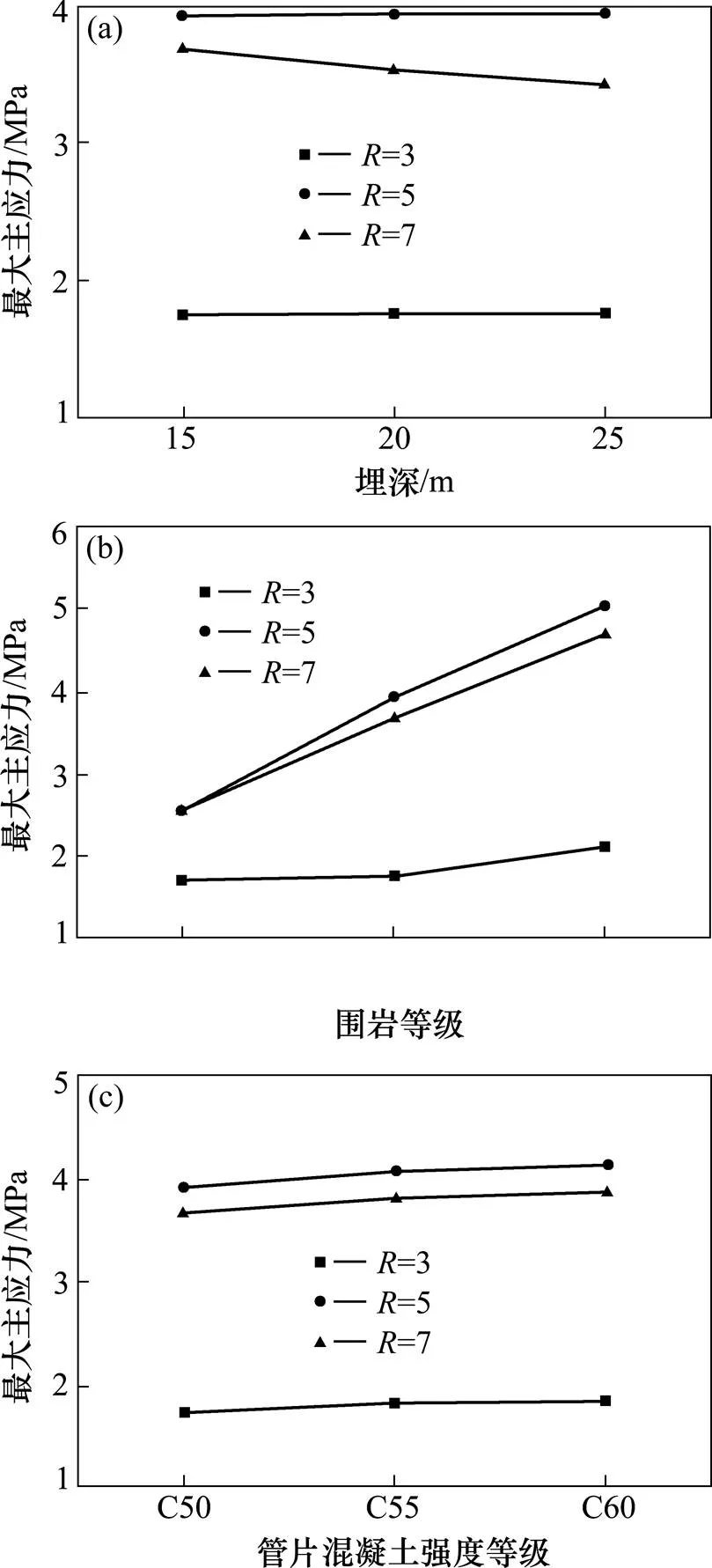
(a) 围岩等级Ⅳ级，混凝土强度C50；(b) 埋深15 m，混凝土强度C50；(c) 埋深15 m；围岩等级Ⅳ级

管片外径对盾构管片拉应力影响较大，小直径盾构管片(=6 m)拉应力最小，大直径盾构管片(=10 m)拉应力最大，大直径盾构管片拉应力和小直径盾构管片拉应力相差较大，最小相差50%。大直径盾构管片拉应力和超大直径盾构管片拉应力相差不大，最大相差不超过15%。

根据图7(b)可得，围岩等级对盾构管片拉应力影响也比较大，盾构管片拉应力随围岩等级增加而增加。小直径盾构隧道，管片拉应力随围岩等级的提高而增加不多，最多增加不超过25%；大直径盾构隧道和超大直径盾构隧道，管片拉应力随围岩等级的提高而迅速增加，最小增加超过75%。

根据图7(a)和7(c)可得，隧道埋深和混凝土强度对盾构管片拉应力影响较小。盾构管片拉应力随隧道埋深的增加的变化率不超过4%，随混凝土强度增加的变化率不超过6%。隧道埋深范围内盾构管片拉应力变化率较小可能与隧道的浅埋有关，混凝土强度范围内盾构管片拉应力变化较小也可能与高强混凝土有关。

以上结果表明，管片外径和围岩等级是盾构管片拉应力的主要影响因素，隧道埋深和混凝土强度是盾构管片拉应力的次要影响因素。

2.3 参数敏感性分析

2.3.1 人工神经网络训练

根据有限元分析结果，建立盾构管片最大拉应力(目标)和影响因素(输入)的人工神经网络模型。

一共创建了81组数据集，然后将它们进一步分为3个子集(训练集，测试集和验证集)，以避免模型的过度拟合[17]。85%的数据用于训练，15%的数据用于验证。训练数据进一步分为训练集(70%)和测试集(30%)。在将数据输入ANN之前需要对数据进行预处理，使得所有输入层变量和输出层变量中心化和归一化。人工神经网络模型数据集见表4。

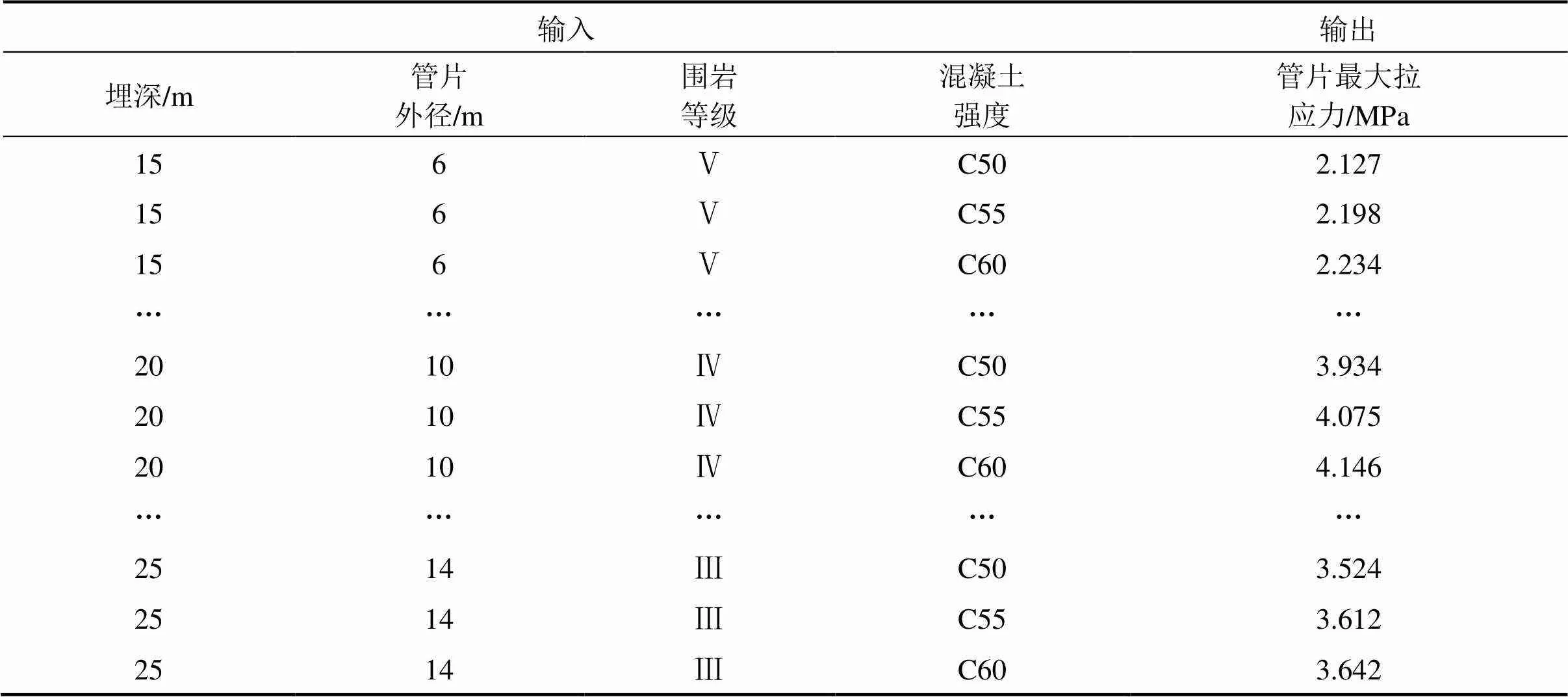
表4 ANN数据集

图8显示了数据集的训练性能，由于测定系数值超过99%，证明了模型具有良好的预测性能，预测值和目标值具有良好的相关性。

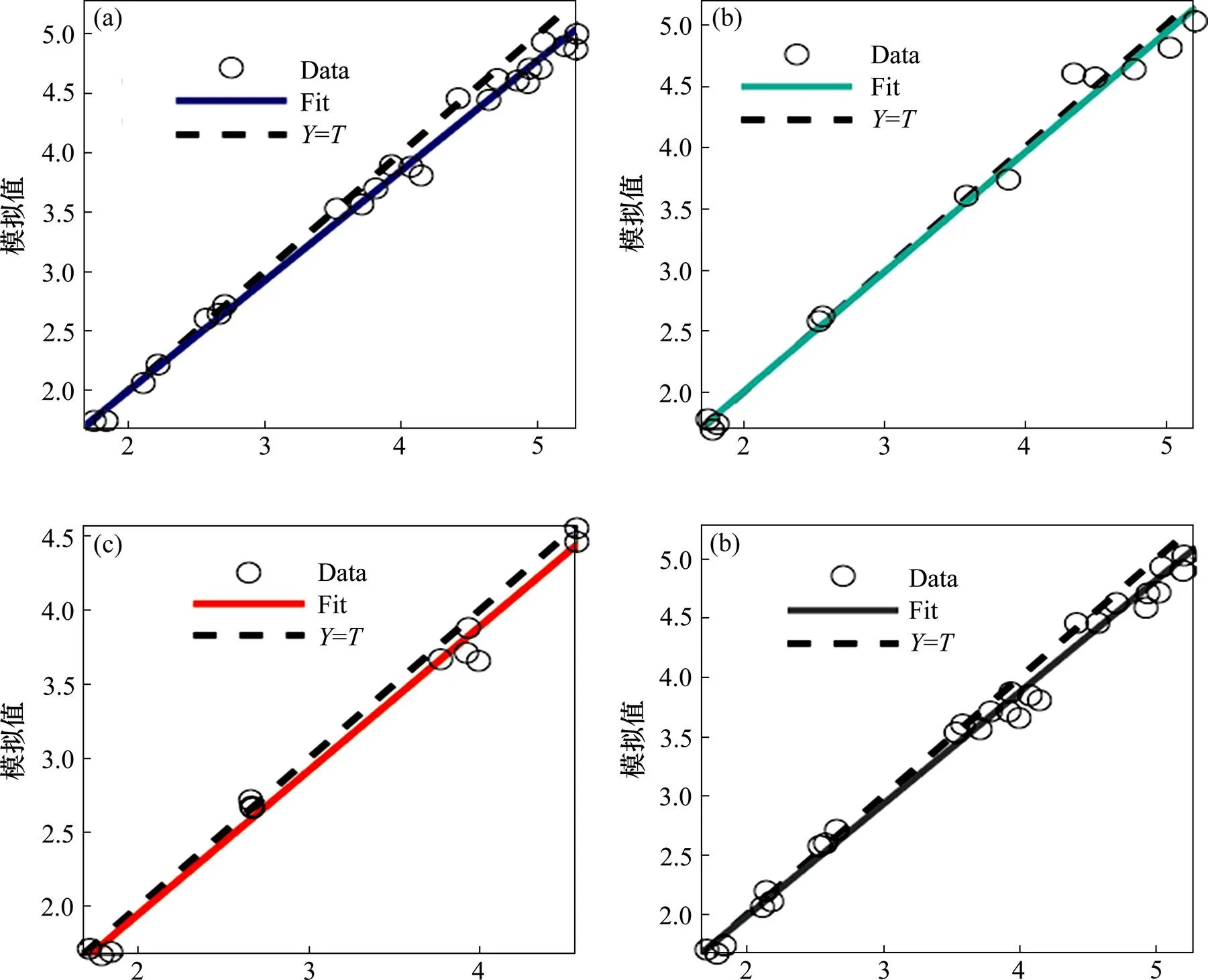
(a) 训练集：R=0.997 15；(b) 验证集：R=0.994 87；(c) 测试集：R=0.994 99；(d) 数据集：R=0.995 96

2.3.2 人工神经网络训练

为进一步分析影响因素对盾构管片拉应力的相对重要性，使用以上训练的数据，按照Garson[12]提出的方法计算影响因素的相对重要性指数。相对重要性指数计算公式如式(1)所示。

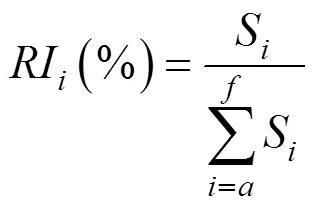
根据图9可得，盾构管片拉应力影响力最大的因素是管片外径，相对重要性指数=54.4%，其次是围岩等级，相对重要性指数=35.3%。隧道埋深和混凝土强度对盾构管片拉应力影响最小，相对重要性指数<6.0%。

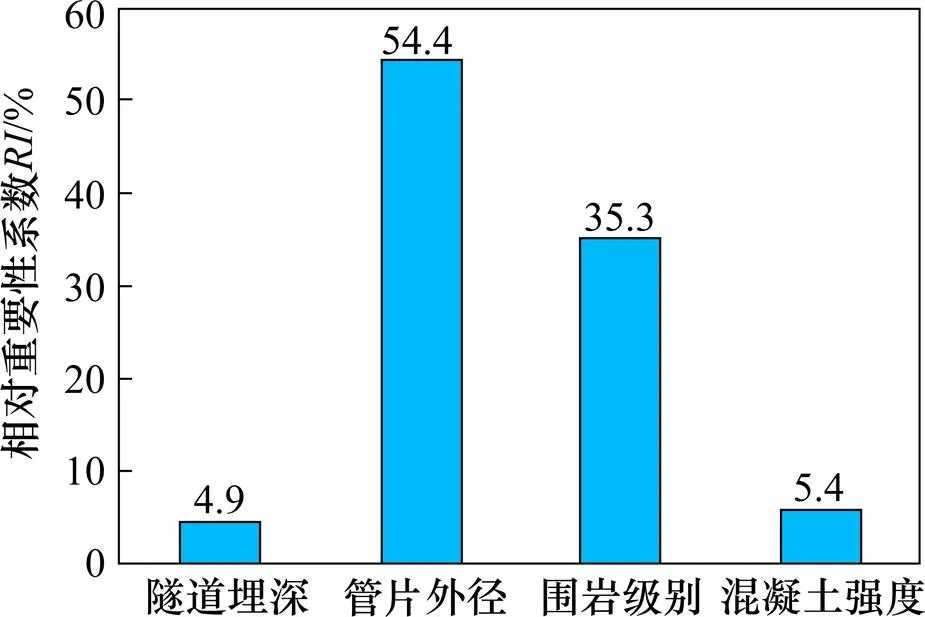
图9 参数相对重要性指数

3 结论

1) 盾构管片接头部位呈现明显的应力集中，接头部位的拉应力和剪应力都比其他位置大。

2) 管片接头的破坏类型为受拉破坏，拱顶和拱腰处管片接头拉应力大于混凝土抗拉强度，剪应力小于混凝土抗剪强度。

3) 盾构管片拉应力影响因素的相对重要性大小关系为：管片外径(=54.4%)＞围岩等级(= 35.3%)＞混凝土强度(=5.4%)＞隧道埋深(= 4.9%)。管片外径和围岩等级是盾构管片拉应力的主要影响因素，隧道埋深和混凝土强度是盾构管片拉应力的次要影响因素。

[1] 唐志成, 何川, 林刚. 地铁盾构隧道管片结构力学行为模型试验研究[J]. 岩土工程学报, 2005, 27(1): 85−89. TANG Zhicheng, HE Chuan, LIN Gang. Study on mechanical behavior of segment of shield tunnel of metro with model test[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 85−89.

[2] 杨雄. 南京长江隧道超大断面管片衬砌结构相似模型试验与数值分析[D]. 成都: 西南交通大学, 2007. YANG Xiong. The similar model test and numerical analysis of the lining structure of the super large section of the Nanjing Yangtze River Tunnel[D]. Chengdu: Southwest Jiaotong University, 2007.

[3] 毕湘利, 柳献, 王秀志, 等. 通缝拼装盾构隧道结构极限承载力的足尺试验研究[J]. 土木工程学报, 2014, 47(10): 117−127. BI Xiangli, LIU Xian, WANG Xiuzhi, et al. Experimental investigation on the ultimate bearing capacity of continuous-jointed segmental tunnel linings[J]. China Civil Engineering Journal, 2014, 47(10): 117−127.

[4] 朱合华, 黄伯麒, 李晓军, 等. 盾构衬砌管片接头内力变形统一模型及试验分析[J]. 岩土工程学报, 2014, 36(12): 2153−2160. ZHU Hehua, HUANG Bolin, LI Xiaojun, et al. Unified model for internal force and deformation of shield segment joints and experimental analysis[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(12): 2153−2160.

[5] 梁英俊. 土层侧压力系数试验测定及其对盾构管片内力的影响分析[D]. 北京: 北京交通大学, 2011. LIANG Yingjun. Test of lateral pressure coefficient of soil layer and its influence on internal force of shield segment[D]. Beijing: Beijing Jiaotong University, 2011.

[6] 宋锦虎, 缪林昌, 徐政, 等. 浅埋并行隧道间距对管片内力影响的分析[J]. 工业建筑, 2012, 42(1): 110−116, 84. SONG Jinhu, MIAO Linchang, XU Zheng, et al. Impact analysis of twin-tunnels apace on internal force in lining [J]. Industrial Building, 2012, 42(1): 110−116, 84.

[7] 丁军霞, 冯卫星, 杜学玲. 盾构隧道管片衬砌内力及变形的影响因素分析[J]. 石家庄铁道学院学报, 2004(3): 75−79. DING Junxia, FENG Weixing, DU Xueling. Analysis of influence factors on internal force and deformation of shield tunnel lining[J]. Journal of Shijiazhuang Railway Institute, 2004(3): 75−79.

[8] 艾辉军. 基于三维非连续接触模型的管片与接头结构力学特性研究[D]. 长沙: 中南大学, 2014. AI Huijun. Study on mechanical properties of tube and joint structure based on three dimensional discontinuous Ashimo H, Ishimura T, Evaluation of the load on shield tunnel lining in grave[J]. Changsha; Central South University, 2014.

[9] Chungsik Yoo. Ground settlement during tunneling in groundwater drawdown environment–Influencing factors [J]. Underground Space, 2016, 1(1): 20−29.

[10] 张鹏. 地铁盾构隧道管片接头的理论分析及应用研究[D]. 北京: 北京交通大学, 2011. ZHANG Peng. Theoretical analysis and application research on the segment joint of metro shield tunnel[D]. Beijing: Beijing Jiaotong University, 2011.

[11] Hornik, K, Stinchcombe M, White H. Multilayer feedforward ntworks are universal approximator[J]. Neural Networks, 1989, 2(5): 359−366.

[12] Garson G D. Interpreting neural-network connection weights[J]. AI Expert, 1991, 6(7): 47−51.

Failure type and parameter sensitivity analysis of shield segment joint

ZHANG Pingping, YANG Weichao, YIN Rongshen, DENG E

(School of Civil Engineering, Central South University, Changsha 410075, China)

The joints of the lining structure, the weak and key parts of the mechanical properties, are the most vulnerable parts of the whole segment. In this paper, the internal force characteristics of the shield segment joint, failure type of segment joint and the relationship between the tensile stress of the shield segment and influencing factors are presented. An artificial neural network (ANN)-based sensitivity analysis was performed to obtain insight into the relative importance of the influencing factors. The results indicates that the failure type of the pipe joint is tensile failure. The diameter of shield segment and the grade of surrounding rock are the primary influencing factor with=54.4% and=35.3%, respectively. The tunnel depth and strength of concrete are the secondary influencing factors with RI less than 6%.

shield segment joint; failure type; maximum tensile stress; relative importance index

10.19713/j.cnki.43−1423/u.2019.02.022

U455.47

A

1672 − 7029(2019)02 − 0450 − 07

2018−02−26

国家自然科学基金青年基金资助项目(5140826)

杨伟超(1978−)，男，河南许昌人，讲师，博士，从事隧道及地下工程方面的教学与科研；E−mail：weic_yang@163.com

(编辑 蒋学东)