钢管混凝土系杆拱桥静力参数敏感性分析

龙汉，刘剑



钢管混凝土系杆拱桥静力参数敏感性分析

龙汉1，刘剑2

(1. 长沙中大建设监理有限公司，湖南 长沙 410075； 2. 中南林业科技大学 土木工程学院，湖南 长沙 410004)

为了研究设计参数对某钢管混凝土系杆拱桥结构响应的影响，对常用3种参数敏感性分析方法进行对比。并在ANSYS有限元模型中选用响应面法(RSM)对钢管混凝土系杆拱桥进行静力参数敏感性分析，求得各设计参数对拱顶位移、拱座水平推力及拱圈内力等结构响应的敏感因子与敏感百分比。研究结果表明：敏感因子能够体现结构响应随着设计参数变化的程度及规律，而根据敏感百分比的大小能更直观地判断出各设计参数对结构响应的重要程度。为钢管混凝土系杆拱桥的参数敏感性分析与参数识别提供参考。

桥梁工程；钢管混凝土系杆拱桥；敏感性分析；响应面法

中承式钢管混凝土系杆拱桥具有造型美观，经济性好，对地基条件适应性好，能充分发挥钢与混凝土2种不同材料性能的优点，目前已成为大跨径桥梁的主要结构型式之一。随着施工工艺的不断进步，中承式钢管混凝土系杆拱桥的跨径也不断增大，对其施工过程中的控制也越发重要。施工控制的前提之一就是对各种设计参数进行识别，判断各设计参数对桥梁结构响应的影响程度，才能有针对性的采用控制措施。而参数识别的手段之一就是进行敏感性分析。国内学者大都采用单一参数调整法进行敏感性分析[1−8]，并没有将结构响应的变化幅度与设计参数的变化幅度联系到一起，具有较大的局限性。张治成[9]在对南浦大桥−中承式钢管混凝土拱桥进行施工控制研究时，采用了梯度分析法进行敏感性分析，并用影响百分比来区分各设计参数对结构响应的影响程度。刘剑等[10]采用响应面法(Response Surface Method，下文简称RSM)对某大跨径斜拉桥进行参数敏感性分析，并根据敏感百分比大小将设计参数对结构响应的影响程度分为4个重要性等级，为桥梁结构参数敏感性分析开拓了新的途径。本文采用ANSYS建立某中承式钢管混凝土系杆拱桥有限元模型，并用RSM进行静力参数敏感性分析，求出材料弹模、容重及荷载等设计参数对拱顶位移、水平推力及拱圈内力等结构响应的敏感因子及敏感百分比，并根据敏感百分比大小定量识别设计参数的重要性等级。将为大跨径同类型桥梁的参数识别及敏感性分析等提供参考。

1 参数敏感性分析方法

1.1 单一参数调整法

目前，国内对于大跨径桥梁结构进行参数敏感性分析多采用单一参数调整法，该方法在有限元模型中分别给定单一参数的变化幅度(一般在3%~ 10%之间)，其他所有参数均保持不变，进行结构计算分析，计算出所关注的结构响应的变化大小，并根据影响程度确定敏感参数和不敏感参数。基本过程如下：

1) 在有限元模型中将某一设计参数变化一定幅度，而其他参数保持不变；

2) 选定结构响应，如节点挠度，截面内力等，利用有限元程序计算修改设计参数前后的结构响应变化值；

3) 根据各设计参数改变前后结构响应值之变化的大小确定出主要及次要设计参数。

单一参数调整法仅仅分析了一定变化幅度下设计参数对结构响应的影响程度，并没有将结构响应的变化幅度与设计参数的变化幅度联系到一起，而且需要多次修改有限元模型进行分析计算，因此具有较大的局限性。

1.2 梯度分析法

考虑到单一参数调整法的局限性，张治成[9]采用梯度分析法对南浦大桥进行施工阶段参数敏感性分析。通过研究目标函数(,)在最优点(,)处对设计参数的梯度值来进行结构参数敏感性分析。该方法假定控制目标函数为=(,)。分析某设计参数x对控制目标的影响敏感性时，可令x在其基准值一定范围内发生变动，而其余参数取基准值不变，对目标函数和约束函数求偏导，即可得到各设计参数的梯度值，分别为

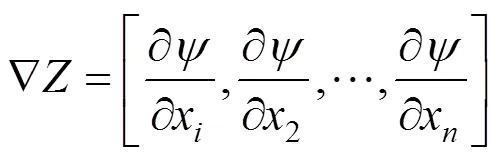
进而得到参数x的敏感函数为

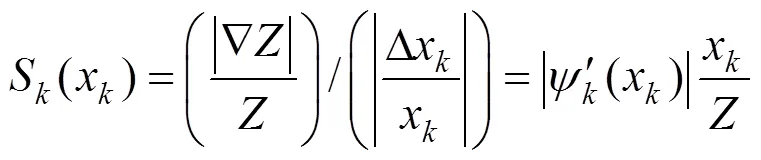
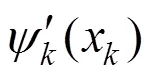
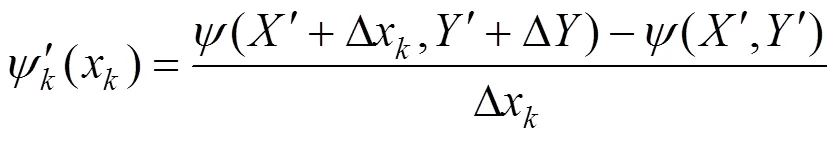
式中：Δx一般取设计变量上下限变化值的1%。

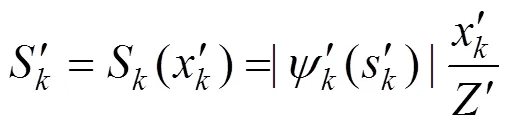
张治成[9]还提出根据影响百分比的大小来比较各设计参数的重要性程度，其计算公式如式(5) 所示。

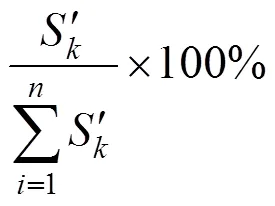
梯度分析法将结构响应的变化幅度与设计参数的变化幅度联系到一起，得到了设计参数对于结构参数的敏感因子及敏感百分比，可以更有效的设计参数对结构进行敏感性程度。但是与单一参数调整法一样，需要多次调整参数对有限元模型进行计算，同样也具有局限性。

1.3 响应面法

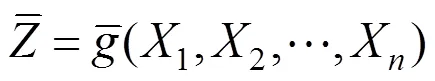
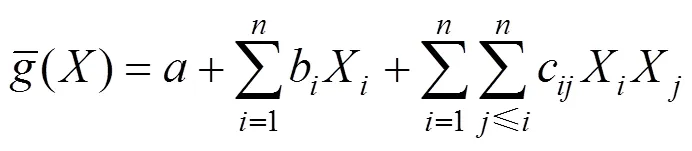
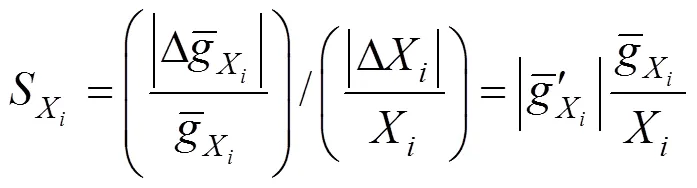
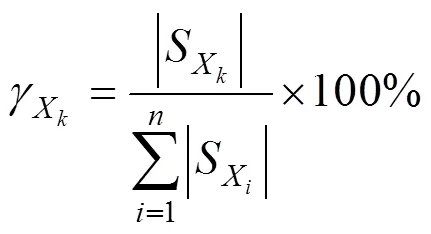
以往学者在进行参数敏感性分析时只是简单的将设计参数分为重要和次要2种类型，而且没有统一的、量化的区分依据，这种做法无疑对于参数敏感性分析及施工过程中的误差控制是不利的。为了更有效的区分各设计参数对结构响应的重要性程度，刘剑等[10]提出将设计参数分为重要、主要、次要及可忽略4种级别(如表1所示)，然后根据敏感百分比的大小就能定量的区分设计参数的重要性程度。

表1 设计参数重要性分类

2 工程简介及有限元模型

本文对某大跨径中承式钢管混凝土系杆拱桥为研究对象，其跨径布置为50 m+280 m +50 m。其中主拱计算跨径=271.5 m，计算矢高=54.3 m，矢跨比/=1/5，拱轴系数=1.5。主拱采用2片拱肋，肋间中心距为19.5 m，拱肋全高5.5 m，全宽2.5 m，上、下弦管各采用2根1 000 mm的Q345钢管，在上下弦并列钢管之间用12 mm厚的Q345缀板连接，腹管采用500 mm×12 mm的空钢管。上下弦管内及缀板间均灌注C50微膨胀混凝土。边拱为等截面悬链线钢筋混凝土拱，计算跨径= 89.35 m，计算矢高=9.1 m，矢跨比/=1/9.819，拱轴系数=1.9。大桥整体布置图及横断面图如图1所示。

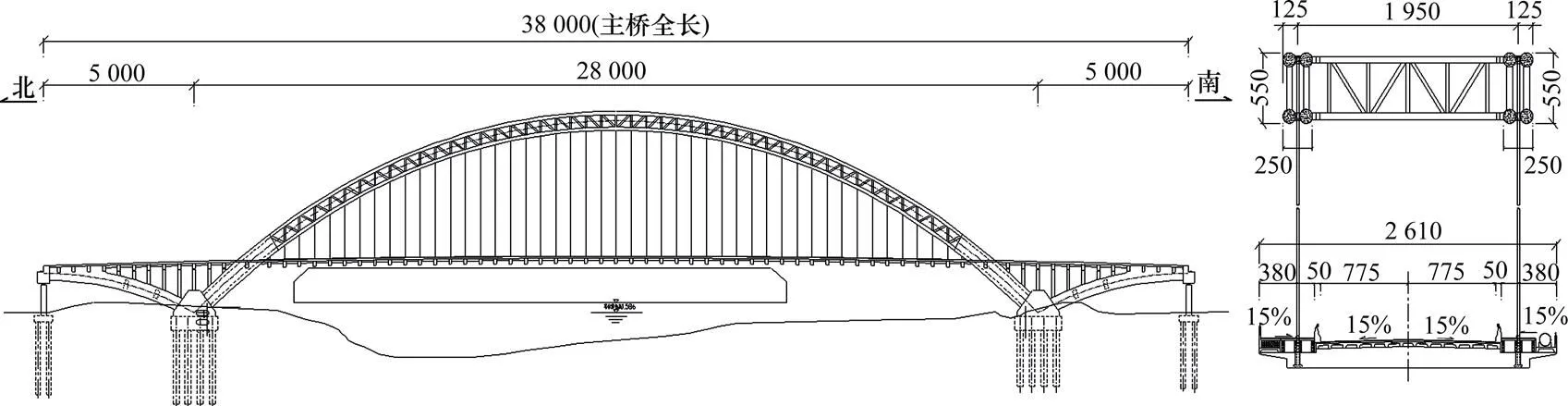
单位：cm

采用ANSYS程序建立全桥有限元模型，模型中共有4 771个单元，6 504个节点。拱肋、纵横梁、横撑及立柱均采用梁单元进行模拟，吊杆及系杆用桁架单元模拟，桥面采用等效均布荷载考虑，有限元模型如图2所示。

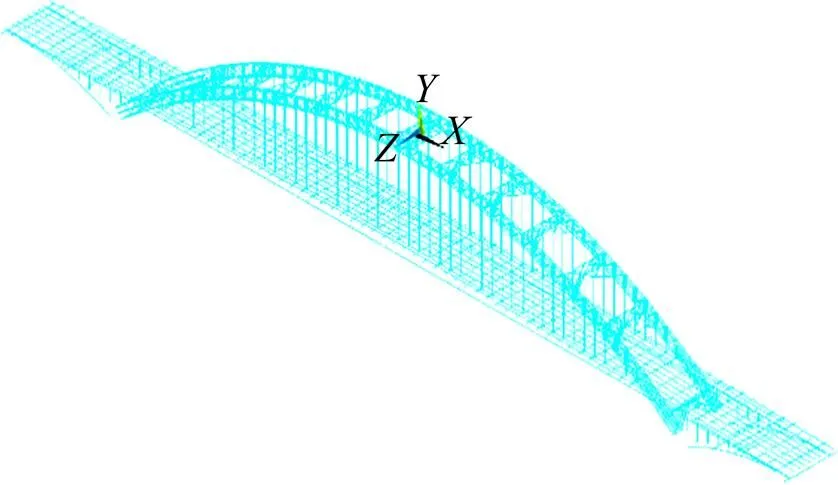
图2 有限元模型图

3 参数敏感性分析

为研究大跨径钢管混凝土拱桥各主要设计参数对结构响应的敏感程度，有限元模型主要考虑钢管弹模E，钢管容重，管内混凝土弹模E1，管内混凝土容重1，边拱混凝土弹模E2，边拱混凝土容重2，系杆张拉应力，纵横梁容重及二期恒载集度这9个设计参数，采用响应面法回归拟合出的近似的结构响应方程，按式(7)与式(8)求得各设计参数的敏感因子与敏感百分比，然后进行参数敏感性分析。由于结果众多，下面仅对主拱拱顶挠度、拱座水平支反力、主拱拱顶截面轴力及弯矩以进行参数敏感性分析。

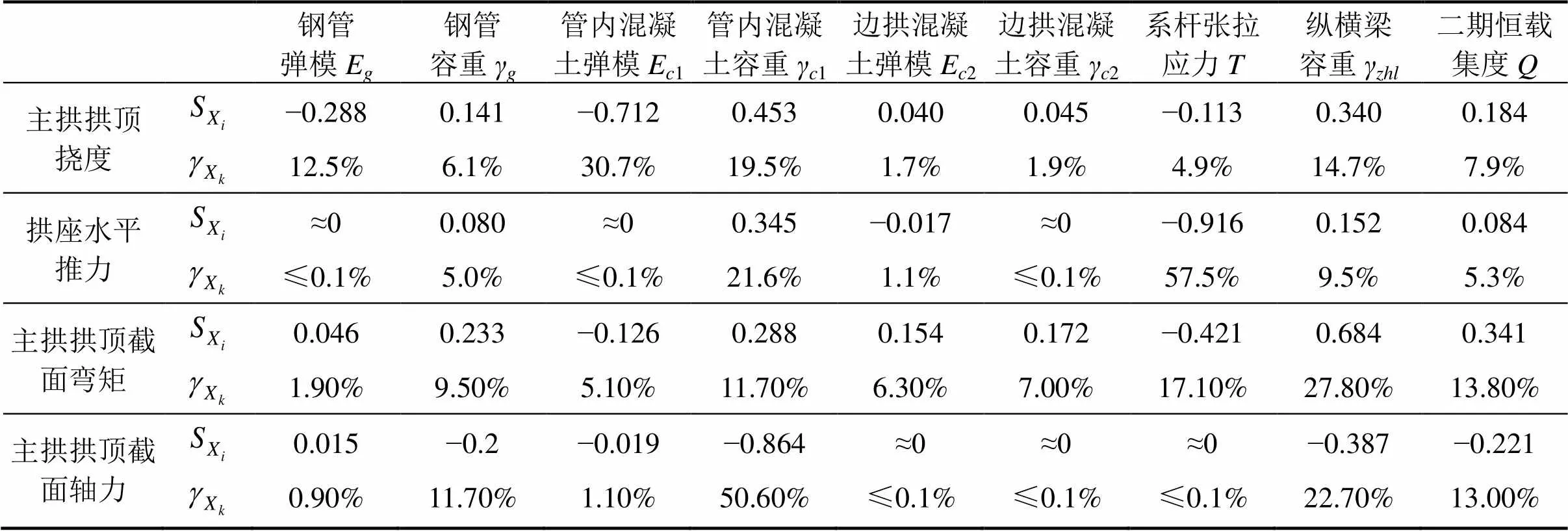
表2 设计参数敏感性分析结果表

模型中将主拱拱顶挠度、拱座水平推力、拱顶截面弯矩及拱顶截面轴力这4个结构响应定义成目标函数，求得各设计参数对其的敏感因子及敏感百分比，计算结果如表2及图3~6所示。

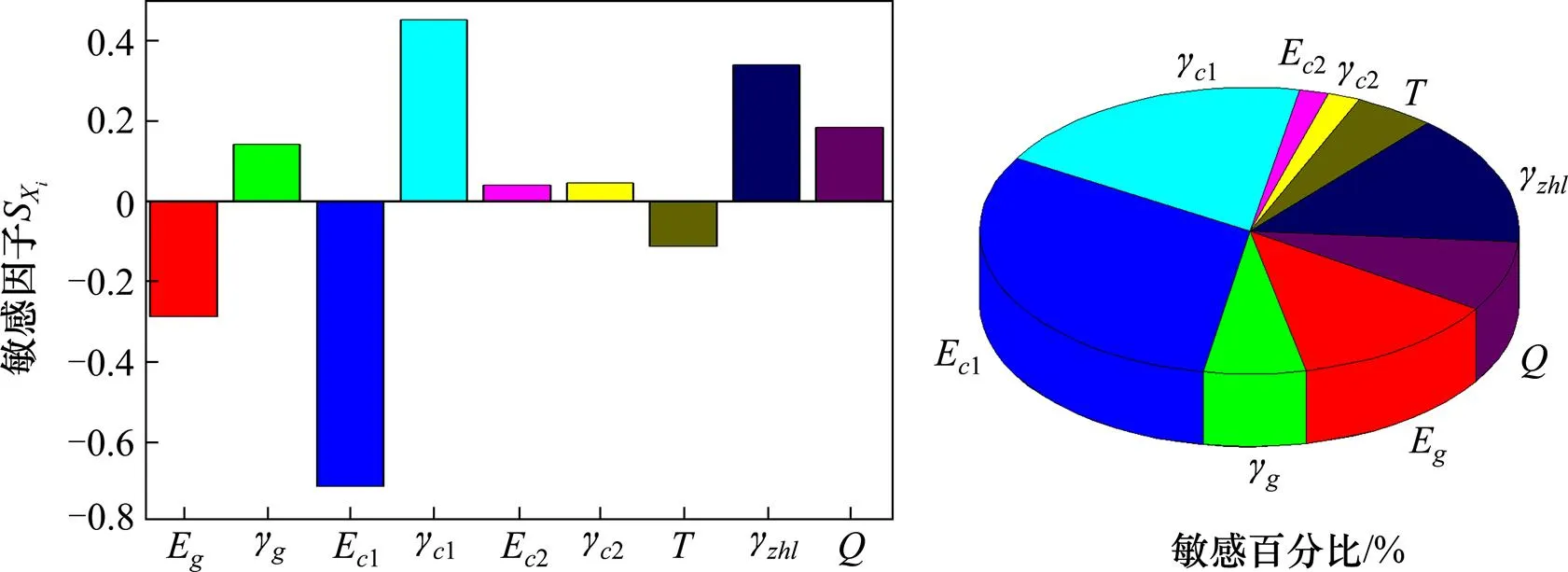
图3 主拱拱顶挠度敏感性分析图

图4 拱座水平反力敏感性分析图

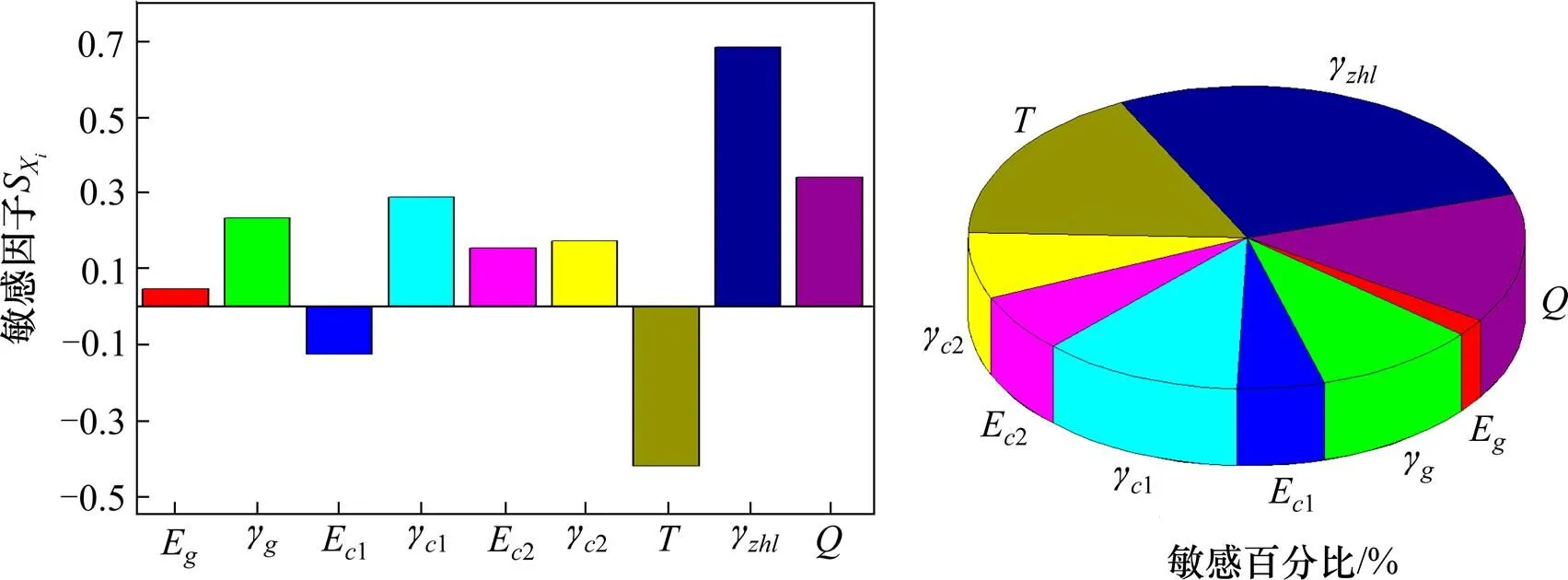
图5 主拱拱顶弯矩敏感性分析图

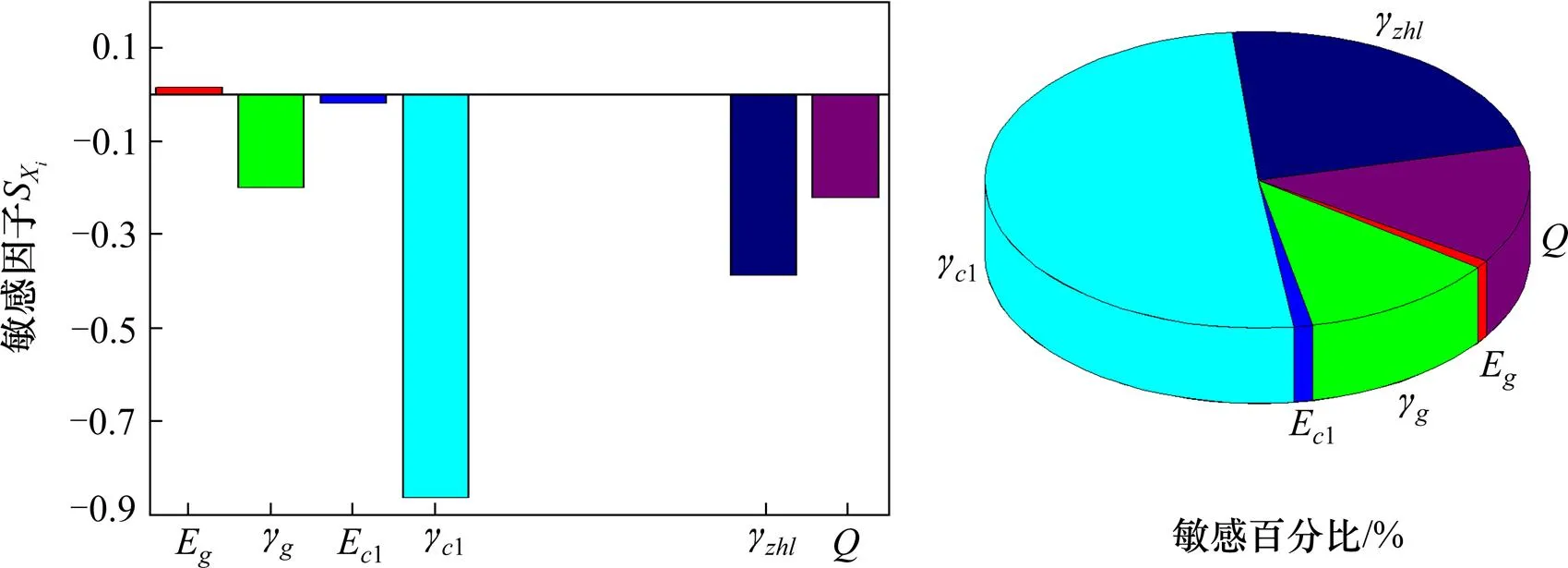
图6 主拱拱顶轴力敏感性分析图

表3 设计参数重要性程度表

根据上述结果，将9个参数的敏感百分比按表1标准分为重要、主要、次要及可忽略参数4个等级，如表3所示。

1) 由表2~3及图3结果分析可知，管内混凝土弹模E1对主拱拱顶挠度的影响最敏感，敏感因子S为0.712，表示E1每增加1%，主拱拱顶挠度要降低约0.712%，E1的敏感百分比为30.7%，是主拱拱顶挠度的主要影响参数，1，，E，及的敏感百分比为6.1%~19.5%，是次要影响参数，而，2，E2的敏感百分比均＜5%，是可忽略影响参数。

2) 由表2~3及图4结果分析可知，系杆张拉力对拱座水平推力的影响最敏感，敏感因子S为−0.916，表示每增加1%，拱座水平推力要降低约0.916%，的敏感百分比为57.5%，是拱座水平推力的重要影响参数，1，，及的敏感百分比处于5%~21.6%之间，是次要影响参数，而其余参数的敏感百分比均≤5%，是可忽略影响参数。

3) 由表2~3及图5结果分析可知，纵横梁容重对主拱拱顶弯矩的影响最敏感，敏感因子S为0.684，表示每增加1%，主拱拱顶弯矩要增加约0.684%，的敏感百分比为27.8%，是主拱拱顶弯矩的主要影响参数；E的敏感百分比为1.9%，是可忽略影响参数；其余参数的敏感百分比位于17.1%~5.1%之间，是次要影响参数。

4) 由表2~3及图6结果分析可知，管内混凝土容重1对主拱拱顶轴力的影响最敏感，敏感因子S为−0.864，表示1每增加1%，主拱拱顶轴力(符号为“-”)要增加约0.864%，γ1的敏感百分比为50.6%，是主拱拱顶轴力的重要影响参数，，，，E1及E的敏感百分比处于22.7%~11.7%之间，是次要影响参数，而其余参数的敏感百分比均≤5%，是可忽略影响参数。

4 结论

1) 采用响应面法进行参数敏感性分析的方法与以往分析方法不同，不用逐一改变设计参数进行多次试算，而是在ANSYS程序中统一将设计参数定义成输入变量，将关注的结构响应定义输出变量，由程序进行抽样计算就可以将结构响应与设计参数之间的隐式关系转换为显式方程。

2) 根据本文参数敏感性分析结果，对主拱拱顶挠度、拱座水平推力、主拱拱顶弯矩及轴力影响最大的参数分别为：管内混凝土弹模、系杆张拉力、纵横梁容重及管内混凝土容重。由此可知某一设计参数影响程度的大小是针对特定结构响应而言的，不同的结构响应下同一设计参数的影响程度可能完全不同。

3) 所采用的参数敏感性分析方法通过拟合的显示方程可以得出各设计参数对于结构响应的敏感因子及敏感百分比，根据敏感因子的大小可以了解结构响应随着设计参数变化的程度及规律，而根据敏感百分比的大小可以直观的区分各设计参数对结构响应的影响程度；可以更直观了解设计参数对结构响应的影响程度，并能更方便的区分各设计参数的重要性，因此可以使大桥在施工控制过程中的参数识别更具有针对性和有效性，亦可为类似桥梁的参数敏感性分析提供参考。

[1] 杜斌, 张兴, 杨令, 等. 大跨公轨两用悬索桥主缆线形的参数敏感性分析[J]. 铁道标准设计, 2018, 62(9): 60−66. DU Bin, ZHANG Xing, YANG Ling, et al. Analysis of cable-shape parameter sensitivity of long span road-rail suspension bridge[J]. Railway Standard Design, 2018, 62(9): 60−66.

[2] 王学伟, 卜一之, 祝兵, 等. 六塔斜拉桥主梁制造阶段参数敏感性研究[J]. 公路交通科技, 2015, 32(1): 76−82. WANG Xuewei, BU Yizhi, ZHU Bing, et al. Analysis on parameter sensitivity at manufacturing stage of main beam of 6-pylon cable-stayed bridge[J]. Journal of Highway and Transportation Research and Development, 2015, 32(1): 76−82.

[3] 郭鹏. 中承式钢管混凝土系杆拱桥施工控制及参数敏感性分析[D]. 合肥: 合肥工业大学, 2016. GUO Peng. Construction control and parameter sensitivity analysis of half-through concrete-filled steel tubular tied arch bridge[D]. Hefei: Hefei University of Technology, 2016.

[4] 周越. 下承式钢管混凝土桁架拱桥模态参数敏感分析[D]. 郑州: 郑州大学, 2013. ZHOU Yue. The sensitivity analysis of a bottom-through concrete-filled steel tube truss arch bridge’s modal parameter[D]. Zhengzhou: Zhengzhou University, 2013.

[5] 刘世明, 刘永健. 无背索曲塔曲梁斜拉桥参数敏感性分析[J]. 公路交通科技, 2014, 31(2): 54−59. LIU Shiming, LIU Yongjian. Analysis of parameter sensitivity for curved-pylon and curved-girder cable- stayed bridge without back-stay[J]. Journal of Highway and Transportation Research and Development, 2014, 31(2): 54−59.

[6] 谢明志, 卜一之, 张克跃, 等. 特大跨度混合梁斜拉桥几何控制法参数敏感性[J]. 长安大学学报(自然科学版), 2014, 34(3): 66−73. XIE Mingzhi, BU Yizhi, ZHANG Keyue, et al. Sensitivity of parameters of super long-span hybrid girder cable-stayed bridge based on geometry control method[J]. Journal of Chang’an University (Natural Science Edition), 2014, 34(3): 66−73.

[7] 刘沐宇, 孙向东, 涂开智, 等. 四塔单索面矮塔斜拉桥结构参数敏感性分析[J]. 华中科技大学学报(城市科学版), 2009, 26(4): 10−14. LIU Muyu, SUN Xiangdong, TU Kaizhi, et al. Sensitivity analysis for the structural design parameters of four-tower extradosed cable-stayed bridge with single plane[J]. Journal of HUST (Urban Science Edition), 2009, 26(4): 10−14.

[8] 刘旭政, 黄平明, 许汉铮. 独塔斜拉桥参数敏感性分析[J]. 长安大学学报(自然科学版), 2007, 35(6): 63−66. LIU Xuzheng, HUANG Pingming, XU Hanzheng. Analysis of parameters’ sensitiveness of cable-stayed bridges with single tower[J]. Journal of Chang’an University (Natural Science Edition), 2007, 35(6): 63−66.

[9] 张治成. 大跨度钢管混凝土拱桥施工控制研究[D]. 杭州: 浙江大学, 2006. ZHANG Zhicheng. Construction control of CFST arch bridge with long span[D]. Hangzhou: Zhejiang University, 2006.

[10] 刘剑, 王达. 基于响应面法的大跨径斜拉桥静力参数敏感性分析[J]. 公路交通科技, 2015, 32(8): 100−106. LIU Jian, WANG Da. Static parameter sensitivity analysis of long-span cable-stayed bridge based on RSM[J]. Journal of Highway and Transportation Research and Development, 2015, 32(8): 100−106.

[11] WEI Chunming, CHEN Huai, WANG Yan. Parameters’ sensitivity analysis of extradosed cable-stayed bridge[J]. Journal of Zhengzhou University (Natural Science), 2007, 39(3): 178−182.

[12] WANG F S. Uncertainties in dynamic soil-structure interaction[J]. Journal of Engineering Mechanics, 1984, 110(2): 308−324.

[13] WANG F S. Slope reliability and response surface method[J]. Journal of Geotechnical Engineering Mechanics, 1985, 111(1): 32−53.

[14] Bucher C G, Bourgund U A. Fast and efficient response surface approach for structural reliability problems[J]. Structural Safety, 1990, 7(1): 57−66.

Static parameter sensitivity analysis of concrete-filled steel tubular tied arch bridge

LONG Han1,LIU Jian2

(1. Changsha Central South University Construction Supervision Co., Ltd, Changsha 410075, China; 2. School of Civil Engineering, Central South University of Forestry and Technology, Changsha 410004, China)

To study the influence degree of design various parameters on the structural response of concrete-filled steel tubular tied arch bridge, three common parameter sensitivity analysis methods was compared. In a finite element model established by ANSYS, response surface method (RSM) was used to carry out parameter sensitivity analysis on this bridge, and obtained sensitive factor and sensitive percentage of various design parameters on some structure responses, such as deflection in the top of main arch, horizontal force of arch abutment, moment and axial force in the top of main arch. The results show: sensitive factor of design parameters can reflect the degree and regularities of the structural response changing with design parameters，while according to the size of the sensitive percentage could quantitatively distinguish the importance of various design parameters on the structural response. The method can offer some reference to the parameter sensitivity analysis and parameter identification of concrete-filled steel tubular tied arch bridge.

bridge engineering; concrete-filled steel tubular tied arch bridge; parameter sensitivity analysis; response surface method

10.19713/j.cnki.43−1423/u.2019.02.018

U443

A

1672 − 7029(2019)02 − 0419 − 07

2018−08−10

国家自然科学基金资助项目(51408615)

刘剑(1979−)，男，湖南衡东人，副教授，博士，从事桥梁结构理论及减隔震研究；E−mail：liegess@126.com

(编辑 蒋学东)