高频扑动微扑翼飞行器多目标优化设计
2019-03-06蒋进郑祥明冯卓群沈欢
蒋进,郑祥明,冯卓群,沈欢
(南京航空航天大学 飞行器先进设计技术国防重点学科实验室,南京 210016)
0 引 言
微扑翼飞行器因其体积小、重量轻、隐蔽性好、成本低等特点,在侦察、监测、搜救等领域具有较好的应用前景,受到越来越多关注[1]。近年来,针对微扑翼飞行器的设计与优化,国内外做了相关的研究[2-3]。发现微扑翼机翼与机身最大载荷随着扑动频率的增加急剧增加,严重影响飞行控制效果和飞行器寿命[4-5]。为解决飞行载荷过大的问题,有学者提出在设计过程中使用高强度、疲劳特性较好的材料以减小对飞行器寿命的影响[6];同时也有学者提出对飞行器加装减震装置和使用多传感器修正姿态的方法,以减小载荷对飞行控制的影响[7-8]。分析可知,上述解决方案一定程度上都会增加整机重量,且不能同时满足要求。
本文针对一种高频微扑翼飞行器,提出以改善载荷在时间域上分布情况为目标的多目标优化模型,基于NSGA-Ⅱ算法以飞行器所受升力峰值和对翼根合力矩峰值最小为目标,得到一组悬停状态下的Pareto最优解,以期为总体设计提供数据选择依据。
1 微扑翼曲柄摇杆机构设计及力学分析
1.1 微扑翼设计
设计的微扑翼如图1(a)所示,由电机驱动,转动经带轮和曲柄摇杆机构转换为机翼的摆动运动(如图1(b)所示),再经过迎角限制装置使机翼保持一定迎角(如图1(c)所示),从而产生升力和阻力。分析可知,机翼的运动主要由曲柄摇杆机构决定,并且电机和带轮可用曲柄转速代替,故选取曲柄摇杆杆机构参数作为主要研究对象。

(a) 微扑翼实物图
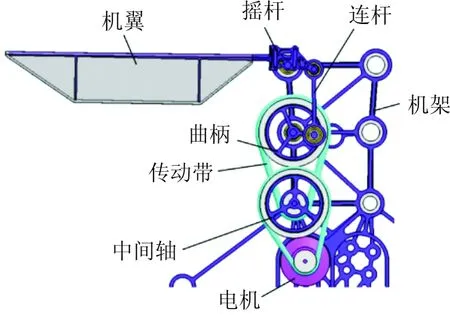
(b) 微扑翼设计图

(c) 机翼迎角限制装置
1.2 曲柄摇杆机构运动模型
曲柄摇杆传动机构简图如图2所示,曲柄逆时针转动,O1,O2为机架上的支点;角θ1是曲柄与水平线的夹角,θ2是连杆与水平线的夹角,θ3是摇杆与水平线的夹角;l1是曲柄长度,l2是连杆长度,l3是摇杆长度,l0是支点间的距离,T为摆动幅角。
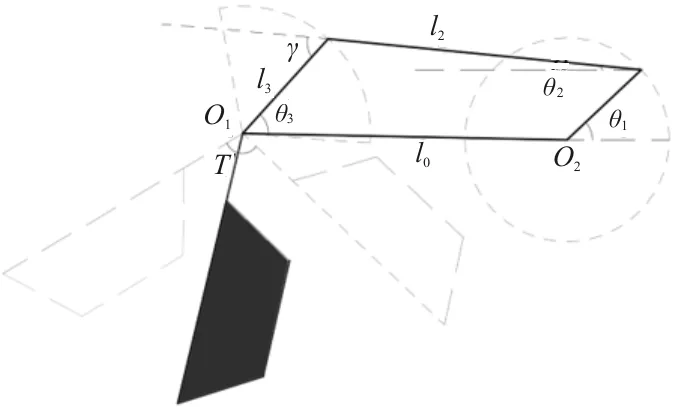
图2 曲柄摇杆机构示意图
设曲柄角速度为ω1,则曲柄与水平线夹角为
θ1(t)=ω1t
(1)
根据曲柄摇杆机构各个参数关系得到摇杆与水平线夹角数学模型为[9-11]:
(2)
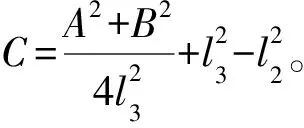
传动角γ公式如下:
(3)
摇杆的角速度和角加速度分别为θ3(t)对时间的一阶导和二阶导。
1.3 微扑翼气动力惯性力模型
为了使机翼始终保持较大迎角,设计机翼具有较大刚度,忽略柔性变形。机翼迎角α(t)≥60°,超过失速迎角,在背流面出现脱体现象,环量存在条件被破坏。通过计算可以得到机翼在运动时雷诺数较小,此时可以采用平板大迎角绕流气动力近似计算公式分析气动力[12]。
则易得机翼升力L(t)、阻力D(t)和机翼对翼根的升力矩ML(t),阻力矩MD(t)为
L(t)
(4)
(5)
ML(t)
(6)
(7)
式中:u(x)=xω3(t)为距离机翼根部x长度处的来流速度;c(x)为弦长;x1和x2分别为机翼翼面的起点和终点;Cπ/2为当迎角为π/2;雷诺数为104~106范围内时,垂直于流动方向的二维平板的压差阻力系数;b为修正系数,取奇数。
经计算,机翼扑动过程中雷诺数约为30 000,满足雷诺数要求,考虑到机翼展弦比较小,同时在扑动过程中会发生柔性变形,与理想情况差距较大,需进行修正,此处Cπ/2取1.68[13],b取1[12]。
机翼翻转的过程迎角α随时间改变,为了准确模拟扑动时状态,使用高频相机进行拍摄,拍摄装置摆放如图3~图4所示。
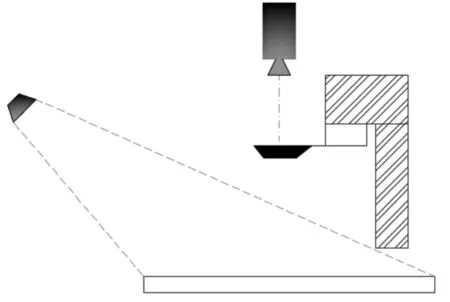
图3 高频拍摄实验装置摆放示意图
得到摄影视频后,将单帧拍摄照片上机翼特征点处(AB=BC)弦长(BD)像素长度与展长(EF)像素长度对比,再根据实际展长即可得到机翼弦长的投影长度,结合实际长度即可得到机翼迎角。

图4 拍摄视频单帧
根据实验数据,进行数据拟合,提出机翼翻转迎角近似公式。
(8)
式中:mod为取余数运算;ai、bi、ci等系数的取值如表1所示。

表1 拟合公式参数表
实验结果与近似曲线对比如图5所示。
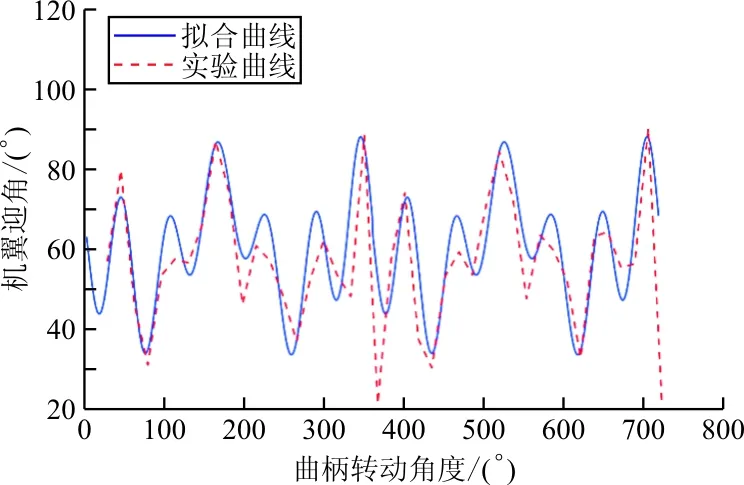
图5 机翼迎角实验测量结果与近似曲线对比
惯性力主要由机翼扑动角加速度引起,只受机翼重量影响。假设机翼质量分布沿展向分布均匀,则机翼惯性力Finer(t)和对翼根处惯性力矩Miner(t)可以表示为[14]
(9)
(10)
式中:m为机翼质量;a3(t)为机翼摆动角加速度。
根据以上模型,可得到合力矩∑M(t)表达式为
(11)
2 多目标优化模型
本文优化目标为:最小化飞行过程中的机翼机身所受载荷峰值。经过计算可得到在两个扑动周期内的机翼机身所受力和力矩变化情况,如图6所示。其中,升力在高频扑动飞行过程中对传感器测量产生较大的噪声,从而影响飞行控制,而合力矩主要影响飞行器寿命,故优化目标可以转化为使飞行过程中升力峰值和合力矩峰值最小。同时为了统一量级,对应量的绝对值平均值进行无量纲化。选取曲柄摇杆机构的四杆长度l1、l2、l3、l0作为优化变量。约束函数对平均升力Lave、四杆长度关系、传动角γ和摆动角T进行限制。最终多目标优化数学模型如下:
(12)
设计变量及变化范围:6mm≤l1≤7mm,16.5mm≤l2≤20.5mm,6.5mm≤l3≤8.5mm,17mm≤l0≤21mm。
约束函数:g1: Lave≥13.32g,g2: l0+l1≤l2+l3,g3: γ≥40°,g4: T≥105°。
其中g1为飞行器最低升力要求,13.32g为设计微扑翼飞行器全机重量的1/4;g2为四连杆曲柄存在约束条件;g3是曲柄机构传动角限制,以保证传动效率;g4是摆动角限制,105°由综合多种高频扑动昆虫鸟类翅膀摆动角度得到[15]。
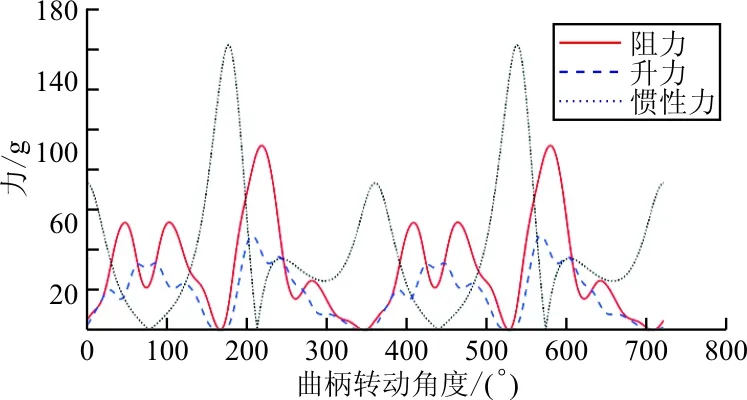
(a) 机翼机身受力变化曲线
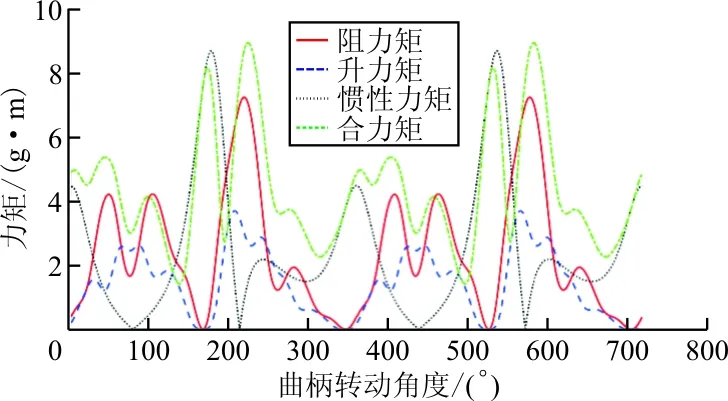
(b) 机翼根部受力矩变化曲线
该优化问题为一个多变量、多约束的非线性多目标优化问题。典型的多目标进化算法有:MOGA(基于排序的适应度赋值多目标遗传算法)、NPGA(小生境Pareto遗传算法)、NSGA(非劣解排序遗传算法)等。其中NSGA算法计算性能较好,采用适应度共享策略,有利于Pareto前沿上的个体分布均匀,维持种群多样性,防止过早收敛。但由于其本身局限性,算法复杂度高达o(MN3)[16-19]。本文采用NSGA-Ⅱ算法提出的快速最优非劣解排序算法,降低算法复杂度至o(MN2),引入精英保留策略,大大提高计算速度[20]。
3 优化结果与分析
运用Matlab平台编写NSGA-Ⅱ程序,代入上述优化模型,在扑动频率为48Hz的情况下,对升力和惯性力在扑动周期内的分布情况进行优化。
设置种群规模为100,交叉概率为0.9,变异概率为0.25,进行1 000代进化后得到该优化的Pareto最优解集[21],如图7所示,可以看出:两个目标函数之间是互相冲突的,在减小一个目标函数的同时必然会牺牲另一个目标函数,因此该优化结果需要进行取舍。
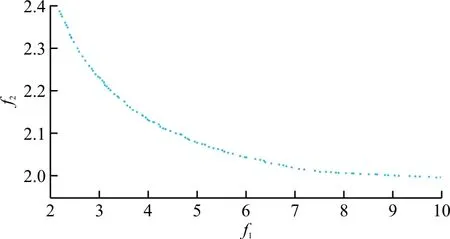
图7 NSGA-Ⅱ算法计算结果
根据微扑翼飞行器设计的具体结构尺寸要求,从最优解集中选取出最合适的几组解如表2所示。

表2 优化前后设计参数对比

表3 优化前后结果对比
为验证NSGA-Ⅱ算法优化效果,选取表中优化后第1组尺寸,得到优化前后机翼摆动角、摆动角速度、升力、合力矩在扑动频率为48Hz(此时飞行器处于悬停状态)情况下的变化曲线对比,如图8所示。
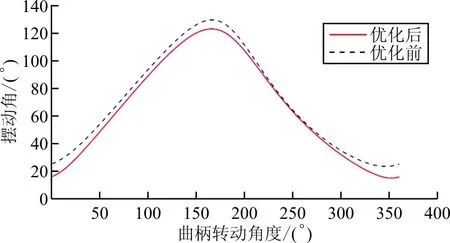
(a) 优化前后机翼摆动角对比

(b) 优化前后机翼摆动角速度对比
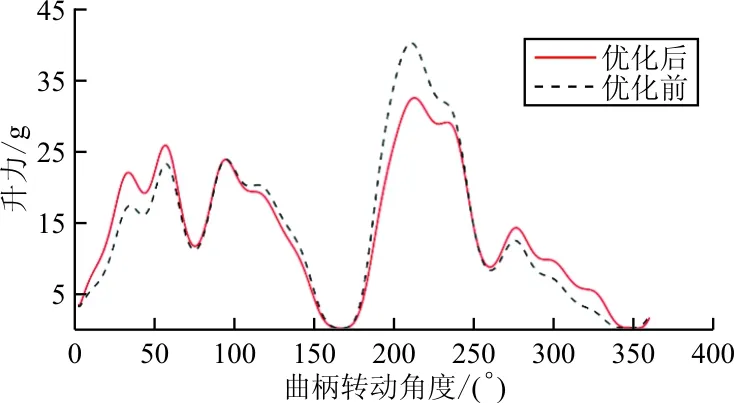
(c) 优化前后升力曲线对比
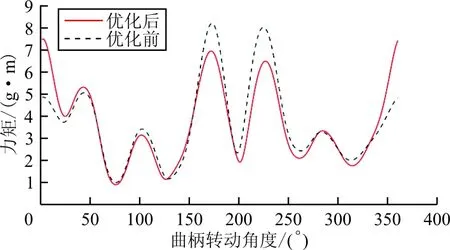
(d) 优化前后惯性力矩曲线对比
从图8可以看出:优化前后机翼摆动幅度增大了2.0°,一定程度上增大了平均升力;机翼翼面第一次翻转变得更为平缓,而第二次翻转速度加快,使翻转过程中产生的载荷分布更为均匀,同时减小了翻转产生的最大载荷;优化使得升力峰值明显降低,升力分布更为均匀,减小飞行过程中由于升力变化引起的飞行性能下降。
为验证优化结果对其他飞行频率也适用,计算得到0~60Hz情况下优化前后平均升力变化曲线(如图9(a)所示),升力和惯性力变化云图(如图9(b)所示)是优化前升力云图,优化后升力云图如图9(c)所示,优化前力矩云图如图9(d)所示,优化后力矩云图如图9(e)所示。
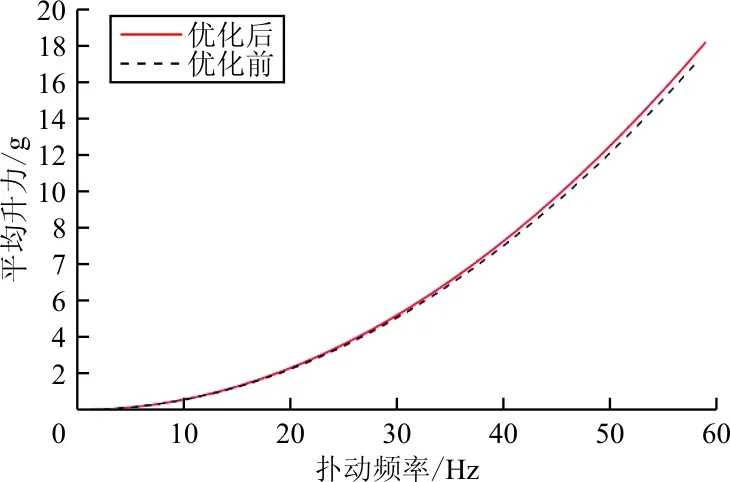
(a) 优化前后平均升力变化曲线
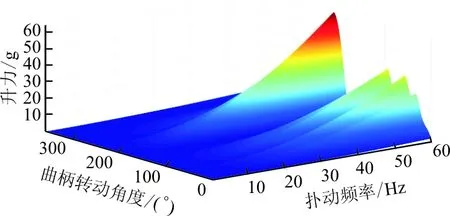
(b) 优化前升力云图
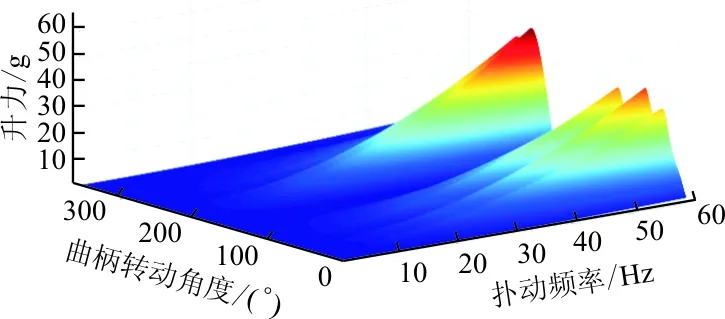
(c) 优化后升力云图

(d) 优化前惯性力矩云图
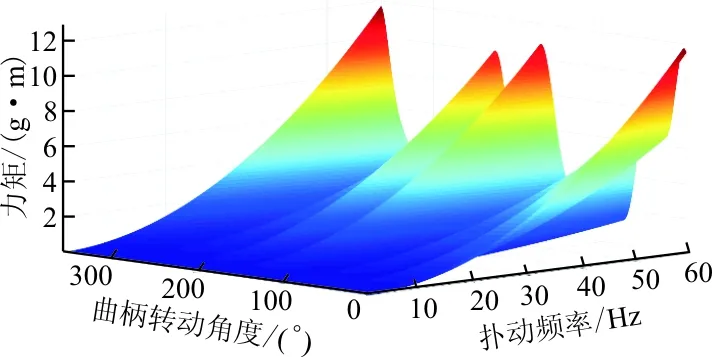
(e) 优化后惯性力矩云图
从图9可以看出:优化后平均升力曲线几乎未变,满足飞行升力需求;同时在其他频率下,升力峰值与力矩峰值也得到降低,故优化结果适用于其他扑动频率。
从表1、表2及图9可以看出:表明优化后的微扑翼飞行器飞行过程中所受最大载荷明显降低,飞行性能和飞行寿命在一定程度上得到改善。后续设计过程可继续使用该优化方法,直至达到设计目的。
4 结 论
(1) 建立优化模型,经优化后,升力峰值与惯性力峰值得到明显降低,飞行器飞行过程中所受载荷分布更为均匀,提高了飞行性能,延长了飞行寿命。
(2) 该优化方法还可为设计者提供多组最优数据以供选择,减轻劳动强度,提高设计效率,符合工程设计需求。
