三维编织复合材料宏细观多尺度传热分析
2019-03-06黄志强聂玉峰李义强
黄志强,聂玉峰,李义强
(1.西北工业大学 理学院,西安 710072)(2.太原科技大学 应用科学学院,太原 030024)
0 引 言
三维编织复合材料具有高冲击韧性、损伤容限与抗疲劳特性,结构可设计性强,能够实现异形件的净尺寸整体成型,可有效保障结构件物理力学性能的稳定性[1-2]。因此,三维编织复合材料在航空、航天等领域得到了广泛应用,而热传导性能是其重要的物理性能之一。面对不断增长的工程应用需求,如何有效表征三维编织复合材料的细观结构并建立细观结构与宏观热传导性能之间的定量关系,已成为材料科学与工程领域的重要课题。
研究三维编织复合材料热传导性能的手段主要有试验方法和数值方法。由于三维编织复合材料组分相种类的多样性及细观结构的复杂性,其热传导性能具有较大的分散性,完全通过试验手段来获取热传导性能是不可取的。数值方法能有效克服试验方法的缺点,从而在预测三维编织复合材料热传导性能中得到了广泛的应用。程伟等[3]采用“米”字型枝状单胞有限元模型和试验方法对三维四向编织复合材料的整体等效热传导系数进行了分析,但所用单胞模型与实际情况相差甚远,模拟结果并不理想;Liu Z G等[4]和李典森等[5]建立了更真实的三维四向编织复合材料单胞模型,该模型区别于以往的“米”字型模型,进一步研究了三维编织复合材料的热传导性能;夏彪等[6]采用周期性非绝热温度边界条件和周期性位移边界条件,建立了三维四向编织复合材料的有限元模型并计算得到有效热传导系数,所得数据比其他文献模型计算结果更接近实验数据;Jiang L L等[7]基于三维四向编织复合材料的螺旋型单胞几何模型,推导了三维四向编织复合材料热弹性问题的稳态热传导分析有限元方程,并对材料进行了稳态热传导分析;Dong K等[8]建立了三维四向编织复合材料的多尺度单胞模型并使用有限元方法分析了热传导性能,包括等效热传导系数和温度场分布;Fang W Z等[9]利用具有多重弛豫时间的格子波尔兹曼模型预测了三维四向编织复合材料的等效热传导系数,并与试验结果进行了对比;Gou J J等[10]发展了多尺寸单胞模型并预测了三维四向编织复合材料的等效热传导系数。
由于三维编织复合材料性能的不均匀性,直接使用传统数值方法时需要非常精细的网格才能捕捉复合材料的局部特征,导致计算规模大幅增加。此外,传统有限元方法很难捕捉三维编织复合材料细观结构对宏观性能的影响,数值模拟结果存在较大的误差。因此,建立一种预测三维编织复合材料热传导性能有效的数值算法是十分必要的。三维编织复合材料具有典型的多尺度特征,而多尺度分析方法考虑了空间和时间的跨尺度与跨层次特征,并耦合相关尺度的物理机理,是求解材料科学和工程问题的重要手段。近年来,基于均匀化理论[11-12],多尺度分析方法被成功用于预测不同复合材料结构的物理和力学性能[13-16]。杨志强等[17-19]发展了多孔复合材料结构的多尺度分析方法,并通过数值算例验证了模型与算法的有效性。而编织复合材料具有更为复杂的细观结构,发展相应的多尺度分析方法具有更为重要的工程应用价值。
本文建立三维四向编织复合材料热传导性能的宏细观多尺度模型,并采用多尺度有限元算法分析三维四向编织复合材料的热传导性能。在此基础上,进一步研究编织角和纤维体积含量对材料热传导性能的影响规律。
1 三维编织复合材料单胞模型
三维编织复合材料具有复杂的空间拓扑关系,受计算机存储的限制,很难对三维编织复合材料整体结构进行分析。考虑到三维编织复合材料细观单胞结构呈周期性分布,本文以细观单胞为研究对象。根据单胞模型空间拓扑几何关系,采用Python语言在Gmsh软件上进行二次开发,建立三维四向编织复合材料的单胞模型,如图1所示(体分比为54%,编织角为41°)。
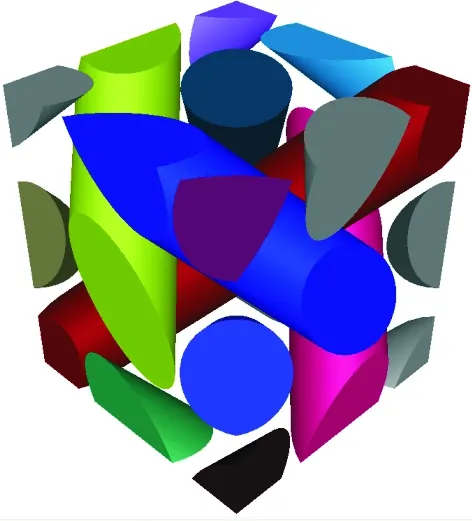
(a) 纤维取向和位置
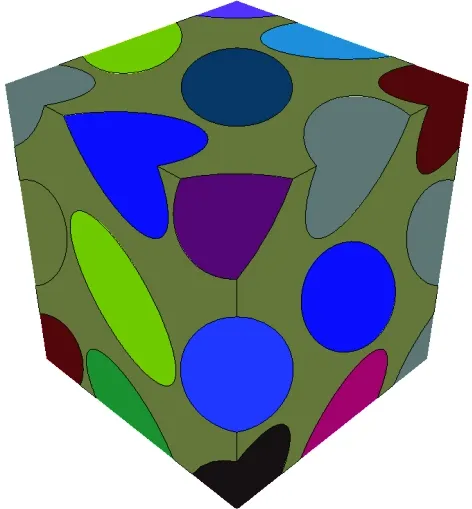
(b) 纤维在基体中的分布
2 宏细观多尺度分析模型
根据上述三维编织复合材料的细观结构表征,考虑如下热传导问题:
(1)
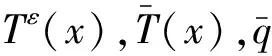

假设在单胞Y内温度场具有如下多尺度渐近展开形式[17]:
Tε(x)=T0(x,y)+εT1(x,y)+ε2T2(x,y)+…
(2)
由于y=x/ε,存在如下链式法则:
(3)
将式(2)~式(3)带入式(1),并整理成ε幂级数的形式,可得:
O(ε)=h(x)
(4)
通过比较式(4)两端ε不同幂次的系数,根据偏微分方程理论可分别定义T0和T1,则温度场的多尺度渐进展开式可定义为
(5)
式中:T0(x)为定义在宏观区域Ω上的均匀化解;Nα1(y)为定义在单胞Y上的一阶局部单胞函数。
Nα1(y)满足如下控制方程:
(6)
(7)
利用上述均匀化系数,可以定义三维编织复合材料结构的均匀化热传导方程:
(8)
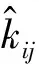
(9)
3 多尺度有限元算法
在对三维四向编织复合材料的几何模型进行有限元网格剖分时,采用网格划分软件Gmsh[20]。将由Python二次开发建立的几何模型导入Gmsh进行剖分,即可得到所需要的有限元网格数据。体分比为54%,编织角为41°的单胞几何模型的四面体网格划分结果如图2所示。
(a) 纤维网格

(b) 单胞网格
基于上述单胞几何模型的建模过程及其有限元网格的划分结果,预测三维四向编织复合材料结构热传导性能的多尺度算法过程如下:
(1) 根据给定的纤维体分比和编织角,利用第1节的建模方法生成三维四向编织复合材料的单胞几何模型;确定复合材料中基体和纤维的热传导系数,并生成有限元网格。
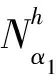

(10)
(11)
(3) 根据已经求出的均匀化热传导系数并确定求解区域Ω的几何构造,使用有限元方法求解边值问题(8),对应的离散变分形式为式(12),得到温度场的有限元解T0h0(x)(h0为宏观区域的有限元网格剖分参数)。
(12)
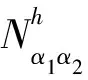
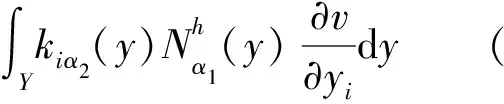
(13)
(5) 基于式(5),由式(14)可计算区域Ω内任一点处温度场的多尺度有限元近似解。
(14)
4 算例分析
为了验证三维四向编织复合材料单胞模型的正确性,并检验多尺度方法用于三维四向编织复合材料热传导性能预测的有效性,数值计算出纤维增强编织复合材料的热传导系数,并与实验结果进行比较。基体的热导率为0.18 W/mK,纤维的横向和纵向热导率分别为1.00和8.00 W/mK。
三维四向编织复合材料横向热传导系数的多尺度计算结果和文献[3]中的实验结果、文献[6-7]中的数值计算结果的对比如表1所示。

表1 横向热传导系数计算结果与文献[3,6-7]的结果对比
从表1可以看出:本文采用均匀化方法得到的横向热传导系数与实验值吻合较好,且比文献[6-7]的预测结果更加接近实验值,但略低于实验值。
三维四向编织复合材料的热传导系数随编织角和纤维体积分数的变化曲线如图3~图4所示。
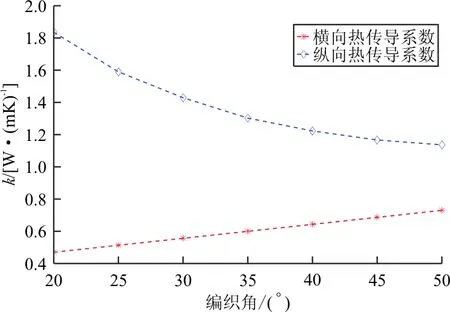
图3 有效热传导系数随编织角的变化趋势
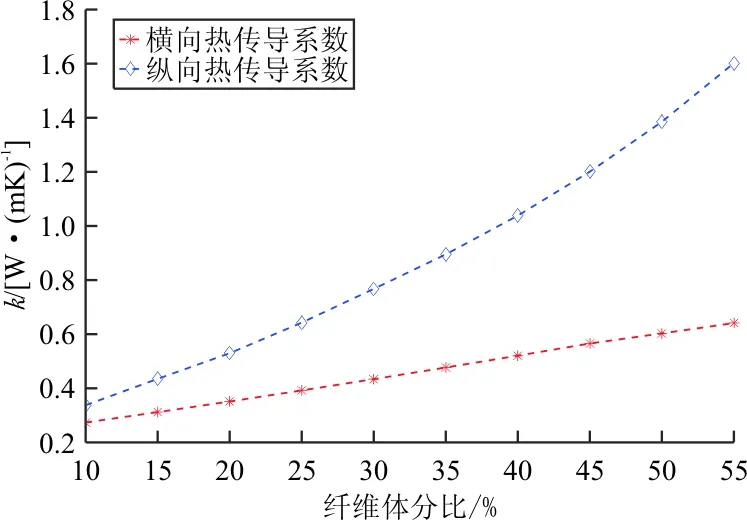
图4 有效导热系数随纤维体分比的变化趋势
从图3可以看出:三维四向编织复合材料的纵向热传导系数整体上高于横向热传导系数,且编织角越小二者之间的差异越明显,表明三维四向编织复合材料的热传导性能具有明显的各向异性特征,且编织角越小,各向异性特征越明显;此外,三维四向编织复合材料的横向热传导系数随编织角的增加而不断增大,而纵向热传导系数随编织角的增加而不断减小,且编织角的变化对纵向热传导系数影响较大。这是因为纤维的热传导系数大于基体,且随着编织角的增大,横向纤维比例增大而纵向纤维比例减小,从而使得三维四向编织复合材料的横向热传导系数提高,而纵向热传导系数降低。
从图4可以看出:当编织角一定时,三维四向编织复合材料的横向和纵向热传导系数都随着纤维体积分数的增加而增加。
三维四向编织复合材料单胞内的温度分布情况如图5所示,可以看出:由于纤维的热传导系数明显大于基体的热传导系数,纤维束所在区域的温度值高于基体区域。此外,由于三维四向编织复合材料的各向异性,单胞的温度分布存在明显的不均匀性,而本文所采用的多尺度分析方法能有效捕捉温度场的不均匀性及局部振荡效应,为三维编织复合材料的热力耦合分析奠定基础。
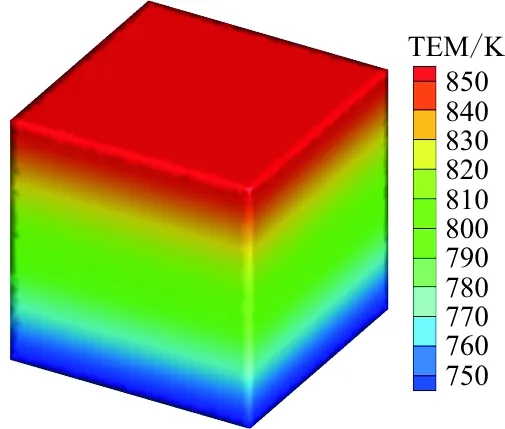
(a) 单胞宏观均匀化温度场分布
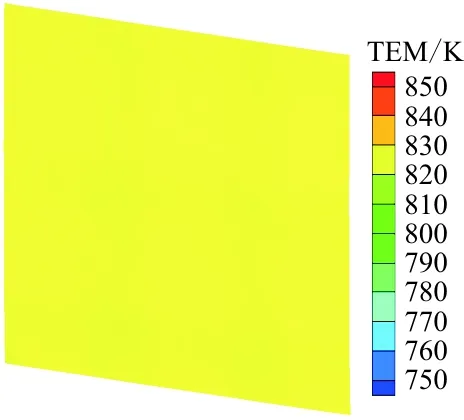
(b) z=0.375处的均匀化温度场分布
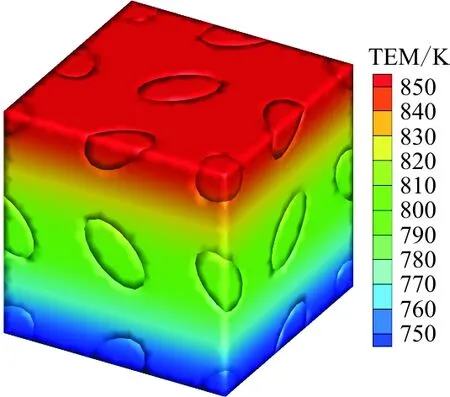
(c) 单胞细观温度场分布
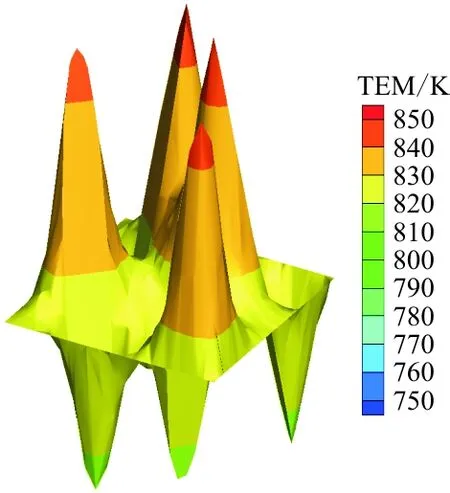
(d) z=0.375处的细观温度场分布
5 结 论
(1) 宏细观多尺度方法能有效预测三维编织复合材料的热传导性能,并且能有效捕捉材料内部的局部振荡效应。
(2) 三维编织复合材料的热传导性能具有明显的各向异性特征,且编织角越小,各向异性特征越明显。
(3) 三维编织复合材料单胞模型中的温度分布表现出明显的不均匀性。
