长输管道凹陷提压回圆评价方法*

帅 义，帅 健，罗小俊，唐 聪,冯 灿,曲文驰

(1. 中国石油大学(北京) 安全与海洋工程学院，北京 102249；2. 北京工业大学 机械工程与应用电子技术学院，北京 100124；3.上海海隆石油管材研究所，上海 200949；4.上海化学工业区公共管廊有限公司，上海 201507；5.中国石油集团西南管道有限公司 南宁输油气分公司，广西 南宁 530012；6.中国石化销售有限公司 华南分公司，广东 广州 510180)

0 引言

管道凹陷是由于管壁受到外部载荷的挤压或碰撞而发生径向位移形成局部塌陷，是管壁发生永久塑性变形而导致管道横截面发生的形状改变[1]。凹陷破坏了管道的结构完整性，严重时甚至影响管道清管器及内检测器的通过。同时，凹陷回圆评价也是管道完整性管理中重要组成部分[2-3]。目前，国内外尚无统一评价方法和处置依据。理论上来讲，针对非约束凹陷(现场开挖后)，增大管道内压，凹陷将会发生回圆，凹陷深度随之减小，这为该工程疑难问题提供了新的思路。目前，国内外对凹陷的回弹及剩余强度研究较多[4-13]，而对凹陷回圆的研究甚少。Baek等[14]对X65管道进行凹陷回圆过程试验，结合数值模拟，探讨了压头尺寸、凹陷深度以及初始内压对凹陷极限回圆率的影响，但是文中未对凹陷的回圆过程的安全性进行论证，且未探讨回圆压力、管材参数以及管道径厚比对凹陷回圆的影响；Rosenfeld等[15]对通过试验和数学理论方法对外载和压力波动下的凹陷深度变化做了详细的研究和描述，指出凹陷的深度变化历程，认为凹陷在内压循环作用下，其深度并非围绕恒定值波动，指出凹陷的回弹与回圆影响管道的疲劳寿命；Alexander等[16]对18根管段微型管做了回圆及疲劳试验，试验过程中的回圆压力取65% SMYS应力水平所对应的内压，详细记录了管道凹陷试验过程中各阶段凹陷的深度，研究认为，当凹陷管道内压从0 MPa逐渐提高到65% SMYS时，凹陷深度回圆量约25%，由于该试验管道尺寸较小，因此，结论不具备普遍性。综上，国内外对管道凹陷回圆还缺乏系统、定量的评价方法，对凹陷回圆的安全性及影响因素有待进一步研究和认识。

基于此，本文采用有限元的方法，对管道凹陷的回圆进行系统研究，对回圆过程中管道的应力应变响应规律进行详细的分析，探讨管道尺寸、管材、凹陷尺寸、初始内压及回圆压力对凹陷回圆系数的影响，寻求管道凹陷回圆系数工程评价方法。

1 管道凹陷回圆的定义

对于非约束凹陷(现场开挖)，在正常操作工况的基础上，提高内压后，凹陷会发生一定的回圆，凹陷深度减小，凹陷局部区域应力、应变随即发生变化。同时，由于管道内压不能无限制的提高，因此认为管道环向应力达到管材屈服强度时所对应的内压为管道的回圆极限压力。为保证管道的安全，规定在对管道进行回圆时的压力不应超过该极限回圆压力。

这里定义凹陷的回圆系数Hpr为提压后凹陷深度hp与提压前凹陷深度hr的比值。容易看出，回圆系数是小于1的，反映了提高内压过程中凹陷的回圆性能。Hpr越小，表示凹陷回圆的程度越大。

(1)

式中：Hpr为回圆系数；hp为提压后凹陷深度，mm；hr为提压前凹陷深度，mm。

2 有限元数值模型

采用ANSYS建立有限元模型，由于凹陷产生过程中压头与管道产生严重挤压，采用20节点六面体单元Solid95进行建模模拟凹陷局部强烈扭曲变形行为。建立1/4对称模型，对凹陷局部区域网格适当加密，而远离凹陷区域网格相对稀疏，以减少计算时间，管道壁厚方向划分4层网格。有限元模型网格划分如图1所示。

图1 有限元模型网格划分Fig.1 Mesh division of the Finite element model

Ramberg-Osgood 模型是1种较好的材料特性曲线拟合模型，应用较为广泛，其表达式如式(2)所示：

(2)

式中：ε为真实应变；ε0为屈服点的弹性应变；ε0=σy/E，E为弹性模量，MPa；σy为屈服强度，MPa；σ为真实应力，MPa ；n为幂硬化指数；α为硬化系数，等于屈服点的塑性应变与屈服点的弹性应变之比，屈服点的塑性应变取0.2%。

在实验室进行管材标准单轴拉伸实验，获取了管材的基本力学参数。拉伸实验结束后，采用上述Ramberg-Osgood模型进行拟合得到材料的真实应力应变曲线，如图2所示。

压头与管道接触具有较强的非线性，采用接触单元进行模拟。在笛卡尔坐标系下施加约束条件，在对称面上加对称边界条件，管道底部轴线上的节点在垂直方向(Y方向)上约束，防止管道在压头加载过程中发生刚体位移。非对称横截面端部节点轴向约束，压头上表面节点采用全约束。由于管道与压头作用过程中具有强烈的多重非线性(接触、几何、材料非线性)，为了提高求解的收敛速度，压头加载采用位移加载方式。其主要载荷加载步骤为：①在管道内表面施加内压；②压头加载至预定深度；③压头卸载；④提高管道内压。有限元模型载荷加载过程如图3所示。

图2 X52，X70和X80钢的真实应力-应变曲线Fig.2 Stress-strain curve of X52, X70 and X80 steel

3 管道提压回圆安全性评价

分析所用管道相关参数为：管径1 016 mm，壁厚15.3 mm，管材X80，压头直径100 mm，加载深度为60.96 mm，管道操作压力8 MPa。为了研究回圆过程中管道应力应变响应状态及安全性，凹陷回圆压力取15.87 MPa，即极限回圆压力(管道环向应力达到管材屈服强度时的压力)。从有限元计算结果中提取数据，凹陷中心点内表面、中间层、外表面3个节点等效弹性应变分量及等效塑性应变分量随载荷步的变化趋势分别如图4和图5所示。

图3 有限元模型载荷加载过程Fig.3 Loading process of the Finite element model

图4 凹陷底部等效弹性应变分量Fig.4 Equivalent elastic strain component at dent bottom

图5 凹陷底部等效塑性应变分量Fig.5 Equivalent plastic strain component at dent bottom

从图4和图5中可以看到，管道凹陷回圆过程中，凹陷区的塑性应变分量基本未发生变化，而3个关键节点的等效弹性应变均发生一定程度的增大，但是均未超过压头加载过程中最大弹性应变0.035 4。这说明，回圆过程中凹陷区主要发生的是弹性恢复，管材并未发生二次塑性损伤，回圆过程中管道是安全的。

同理，取凹陷中心内表面、中间层、外表面节点等效应变和等效应力数据随载荷步的变化曲线，分别如图6和图7所示。从图6和图7中可以看到，凹陷回圆过程中，凹陷区等效应变基本不变，而等效应力发生一定程度的增大，但是均未超过压头加载过程中等效应力最大值750.278 MPa。综合来看，在极限回圆压力下，管道凹陷的回圆过程是安全的。

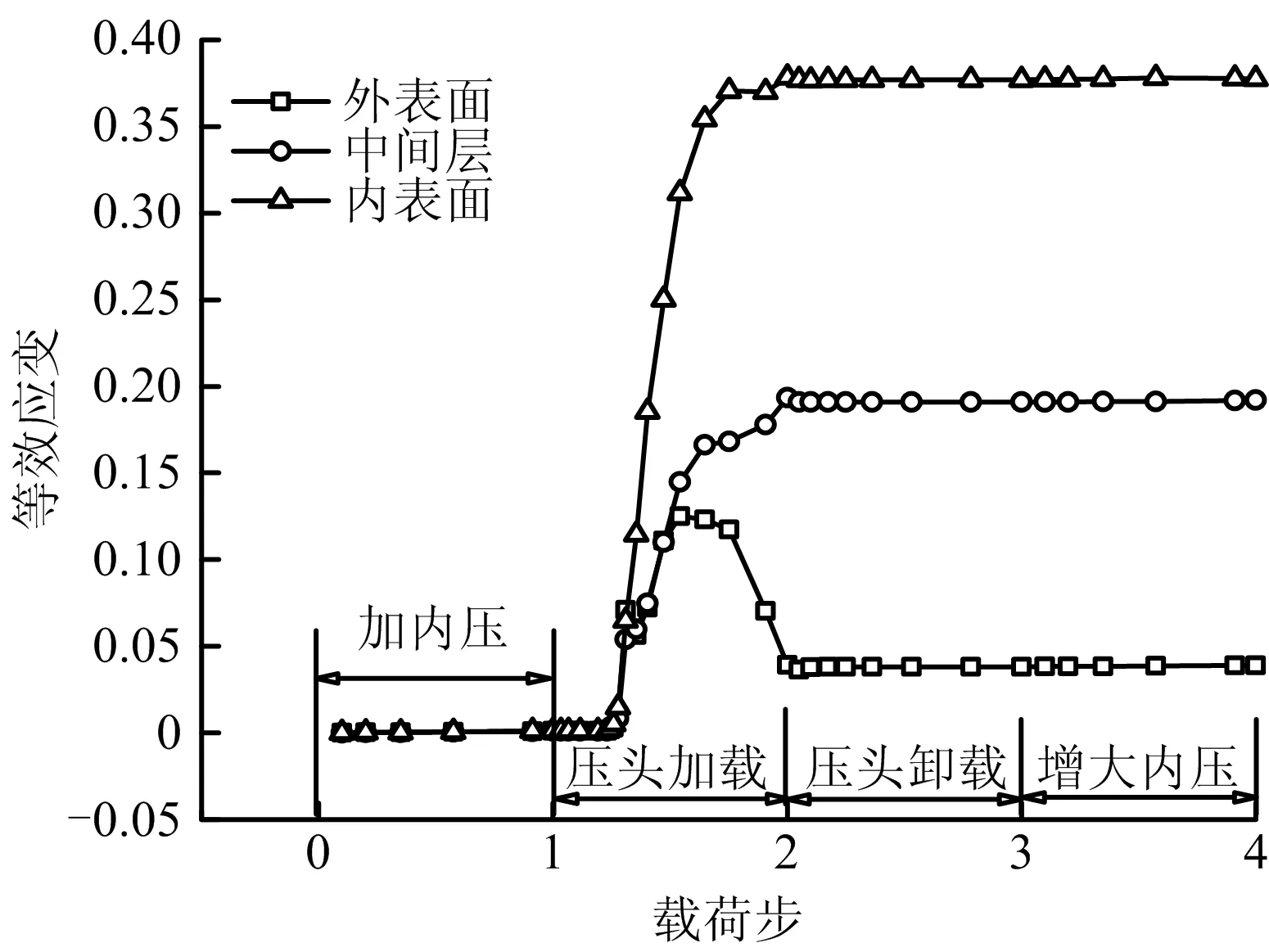
图6 凹陷底部Mises等效应变Fig.6 Mises effective stress changes at dent bottom

图7 凹陷底部Mises等效应力Fig.7 Mises effective strain changes at dent bottom

4 影响因素分析

凹陷回圆的主要影响因素有凹陷深度、管道径厚比、管材性能、管道初始内压以及回圆压力，由于凹陷的回圆是通过提高管道内压来实现的，是利用压力差驱使凹陷区域管壁径向向外鼓起的过程。因此，回圆压力通常高于操作压力。另外，压头尺寸与凹陷尺寸存在一定的联系，为了简化计算，这里只考虑凹陷长度因素，通过改变压头尺寸来研究凹陷长度对凹陷回圆系数的影响。

4.1 外载卸载后凹陷深度的影响

为分析不同凹陷深度对回圆系数的影响，相关计算参数设定如下：管径1 016 mm，壁厚15.3 mm，压头直径100 mm，管材X80，初始内压8 MPa，回圆压力15 MPa，外载相对深度取1%～12%。计算得到不同凹陷深度下回圆系数，如图8所示。由图8可见，回圆系数随着凹陷深度的增大而增大，随着深度增大到一定程度，回圆系数增大的幅度逐渐趋向平缓。这是由于凹陷深度达到一定程度后，塑性变形占主导作用，弹性恢复较小，回圆作用不明显。

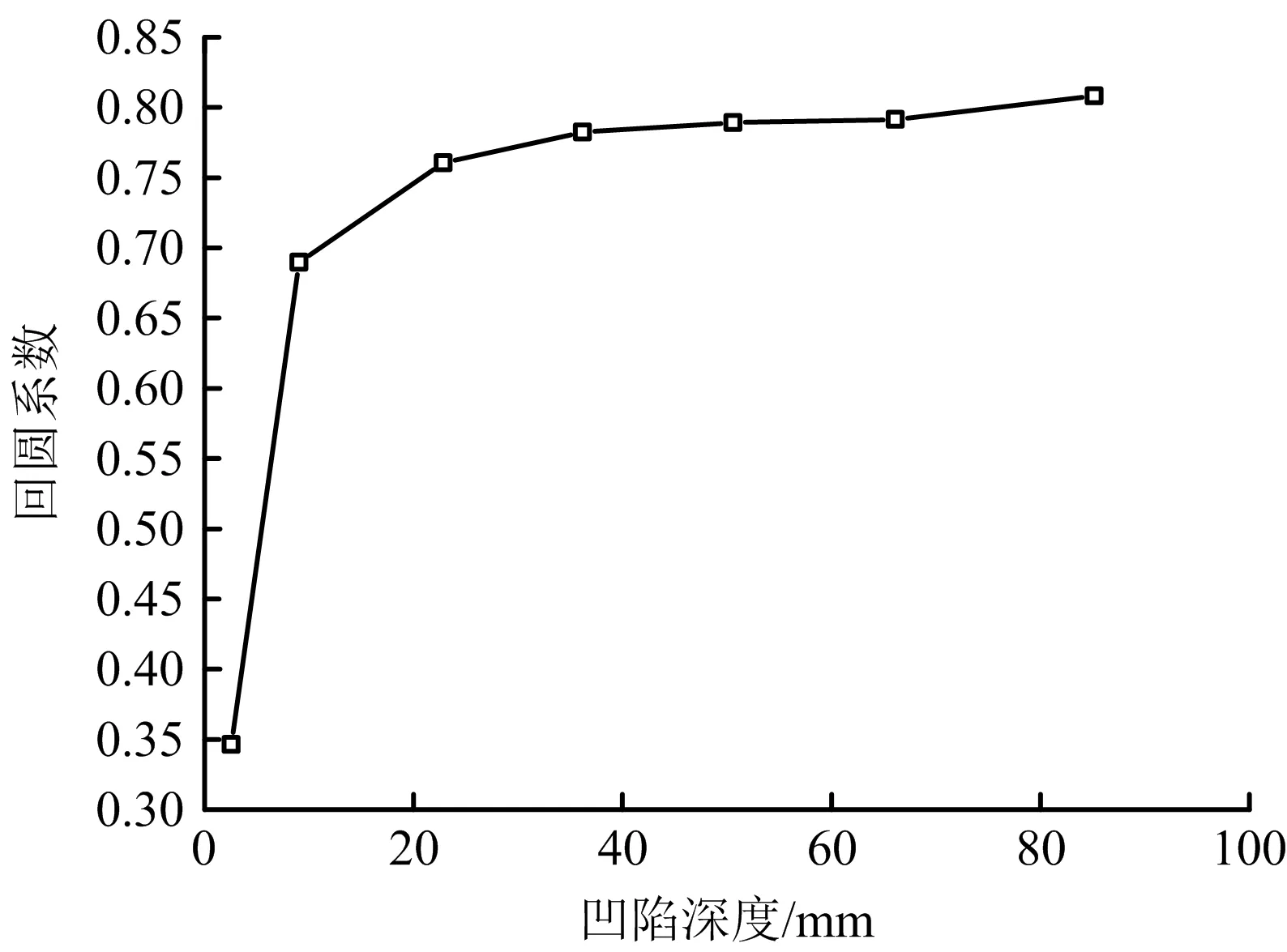
图8 凹陷深度对回圆系数的影响Fig.8 Influence of dent depth to rerounding factor

4.2 凹陷长度的影响

为分析不同凹陷长度对回圆系数的影响，计算参数设定为：管径D为1 016 mm，壁厚t为15.3 mm，管材X70，初始内压8 MPa，回圆压力16 MPa，压头移除后凹陷相对深度取3.4%。计算压头直径在40～320 mm时不同凹陷长度下回圆系数，结果如图9所示。由图9可见，凹陷回圆系数受凹陷长度的影响较大，随着凹陷长度的增大凹陷回圆系数直线减小。这是因为，凹陷越长，其局部受压面积越大，越容易发生回圆。

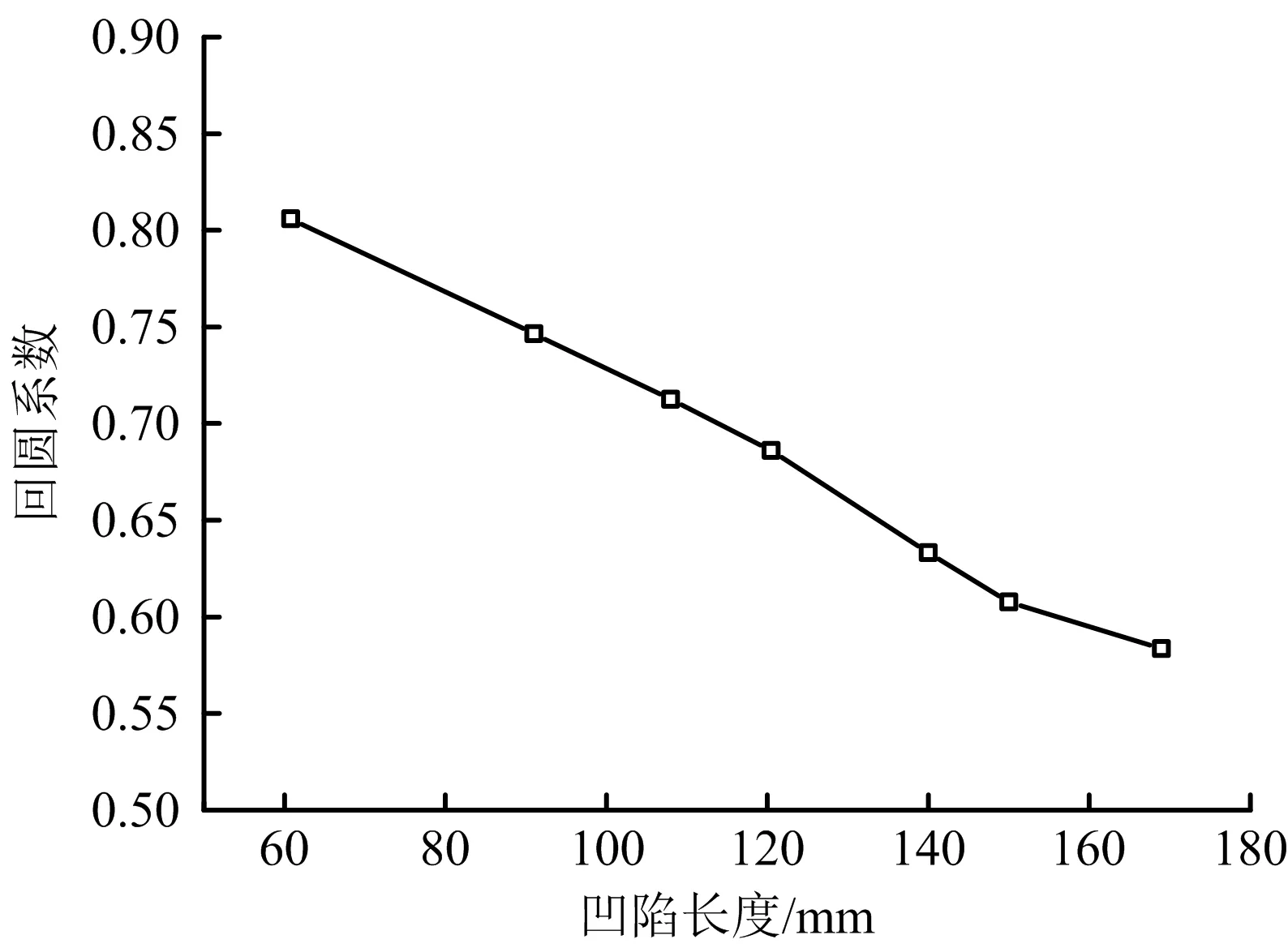
图9 凹陷长度对回圆系数的影响Fig.9 Influence of dent length to rerounding factor

4.3 管道径厚比的影响

为分析管道径厚比D/t对回圆系数的影响，有限元模型计算参数如下：管材X80，管道初始内压6 MPa，回圆压力13 MPa，压头直径160 mm，计算不同径厚比管道凹陷的回圆系数如表1所示。从表1中可以看到，管道径厚比越小，其回圆系数越大；管径相同情况下，壁厚越大，回圆系数越大，凹陷回圆率越小；壁厚相同条件下，管径越大，回圆系数越小，凹陷回圆率越大。管道径厚比是凹陷回圆系数重要影响因素。相比之下，管径对凹陷回圆系数的影响比壁厚的影响更大。

表1 径厚比对回圆系数的影响Table 1 Influence of diameter-thickness ratio to rerounding factor

4.4 初始内压的影响

管道初始内压与回圆压力的压差直接影响凹陷回圆的程度，因此必须要考虑管道初始内压的影响。管径取1 016 mm，壁厚15.3 mm，管材X80，压头直径160 mm，压头移除后凹陷相对深度3.5%，回圆压力16 MPa，计算初始内压为2～12 MPa时凹陷的回圆系数，结果如图10所示。从图10中可以看到，凹陷的回圆系数随着初始内压的增大而增大，初始内压为12 MPa时的回圆系数为0.824，而初始内压为2 MPa时的回圆系数为0.577，两者相差近30%。可见，初始内压对回圆系数的影响较大，应该作为主要考虑因素。

图10 初始内压对回圆系数的影响Fig.10 Influence of initial internal pressure to rerounding factor

4.5 回圆压力的影响

回圆压力为凹陷回圆过程的推动力，其大小直接影响凹陷最终回圆程度。计算参数为：管径720 mm，壁厚10 mm，管材X52，管道初始内压4 MPa，压头直径100 mm，压头卸载后凹陷相对深度4%，计算得到回圆压力分别为5～10.55 MPa时凹陷回圆系数，如图11所示。从图11中可以看到，回圆压力越大，凹陷的回圆系数越小，回圆率就越高；并且，当回圆压力增大到一定程度，回圆系数减小的速率有增大趋势。回圆压力为5 MPa时，其回圆系数为0.961，而当回圆压力为10.55 MPa时，回圆系数为0.599，两者相差0.362，这说明回圆压力对凹陷回圆系数的影响较大。

图11 回圆压力对回圆系数的影响Fig.11 Influence of re-rounding pressure to rerounding factor

4.6 材料参数的影响

材料参数主要考虑屈服强度以及幂硬化指数对凹陷回圆系数的影响。管径660 mm，壁厚9.3 mm，初始内压4 MPa，回圆压力8.5 MPa，压头直径60 mm，压头卸载后凹陷相对深度5.5%，幂硬化指数n=16，屈服强度分别取420～540 MPa，计算不同屈服强度下凹陷的回圆系数如表2所示。从表2中可以看出，凹陷的回圆系数随屈服强度的增大而略微增大，但是其影响十分有限。屈服强度为420 MPa时，回圆系数为0.845，屈服强度为540 MPa时，回圆系数为0.870，两者仅相差0.025。

表2 屈服强度对凹陷回圆系数的影响Table 2 Influence of yield strength of the pipeline

同理，在其他参数相同屈服强度为480 MPa的情况下，计算不同幂硬化指数对凹陷回圆系数的影响，结果如表3所示。从表3中可以看到，回圆系数随幂硬化指数的增大略微增大，但是其影响甚微。幂硬化指数分别为14和22时，两者所计算的回圆系数仅相差0.004。这说明幂硬化指数对回圆系数的影响很小，几乎可以忽略。

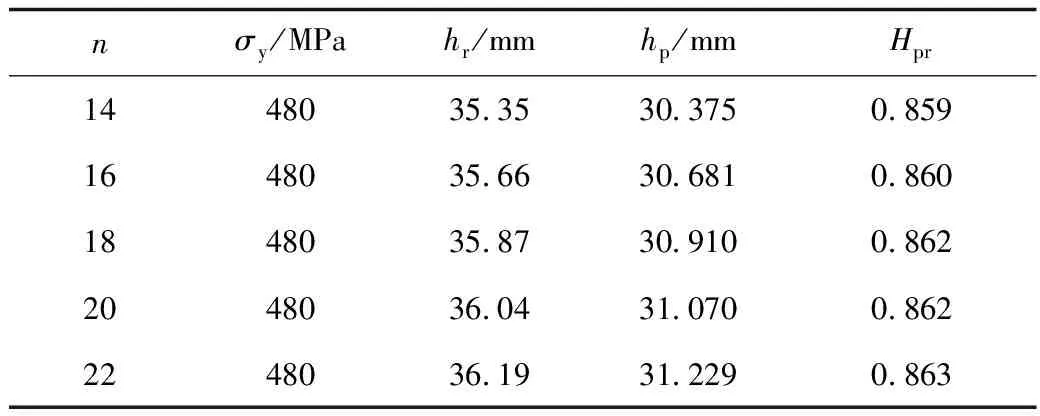
表3 幂硬化指数对凹陷回弹的影响Table 3 Influence of power hardening exponentto

5 回圆系数计算方法

管道凹陷深度达到一定程度时，影响管道内检测器或清管器的通过，采用管段局部提压回圆的技术可使凹陷深度达到检测器或清管器允许通过深度，这就需要定量计算凹陷回圆后的深度，以便确定合适的回圆压力。因此，有必要开发凹陷回圆系数工程预测公式，方便工程应用。

通过对凹陷回圆系数的影响因素分析可以看到，管道初始内压、回圆压力、径厚比、凹陷深度及长度为回圆系数的主要影响因素，而管材参数对凹陷回圆的影响有限，可以不考虑。综合考虑这些主要影响因素，并结合量纲一致性原则，通过多种不同形式的回归试拟合，得到最优的拟合形式为：

(3)

式中：Ph为回圆压力，MPa；P0为初始操作压力，MPa；Lr为提压前凹陷的长度，mm；D为管道外径，mm；t为管道壁厚，mm；a，b，c，d和e为待确定系数；Hpr为回圆系数；hp为提压后凹陷深度，mm；hr为提压前凹陷深度，mm。

采用有限元计算算例对式(3)进行拟合，得到凹陷回圆系数工程计算公式如下：

(4)

将有限元计算结果与所拟合公式计算值进行对比，拟合结果相对误差如图12所示。相对误差平均值为7.03%，最大相对误差为16.54%，误差较小，式(4)可用于工程回圆系数的计算。

图12 拟合结果相对误差Fig.12 Relative result comparison of formula and FEM

6 结论

1)通过应力应变响应分析，认为在极限回圆压力工况下，回圆过程中凹陷区管材主要发生的是弹性恢复，管材并未发生二次塑性损伤，回圆过程是安全的。

2)凹陷的回圆系数随着凹陷深度的增大而增大，深度达到一定程度，其增大的幅度逐渐趋向平缓；回圆系数受凹陷长度的影响较大，且随着凹陷长度的增大而直线减小；管道径厚比越小，管道对应的回圆系数越大；管径对凹陷回圆系数的影响比壁厚的影响更大；凹陷的回圆系数随着初始内压的增大而增大，随回圆压力的增大而减小；管材参数对凹陷的回圆系数影响不大。

3)基于非线性有限元方法，开发出了管道凹陷回圆系数定量预测方法，具有一定的工程应用价值。