大尺寸通风管网中障碍物对瓦斯爆炸冲击波传播特性影响的数值模拟*

孟亦飞，董铭鑫，赵东风，贾进章

(1.中国石油大学(华东) 化学工程学院，山东 青岛 266580；2.中国石油大学(华东) 机电工程学院，山东 青岛 266580；3.辽宁工程技术大学 安全科学与工程学院，辽宁 阜新 123000)

0 引言

瓦斯爆炸作为严重的煤矿灾害之一，严重威胁着煤矿的安全生产。为了防治瓦斯爆炸事故，降低瓦斯爆炸带来的危害和损失，国内外学者在地面采用实验方法对单条管路或简单分叉管路中的瓦斯爆炸传播特性进行了广泛研究[1-5]。国内方面，林柏泉等[6]、叶青等[7]对受限空间内障碍物、分叉管道、拐弯管道、连续拐弯管道、T型管道以及变径管道对瓦斯爆炸冲击波、火焰波的影响进行了一系列研究；蔺照东等[8-9]研究发现，障碍物改变了爆炸冲击波的传播规律，随着障碍物数量和尺寸的增加，激励作用越明显；余明高等[10]发现管道中障碍物的位置会对瓦斯爆炸过程产生显著的影响；秦涧等[11]通过实验发现，不同形状的障碍物对瓦斯爆炸的最终结果影响不同，挡板状的障碍物更易促进瓦斯爆炸，多孔状障碍物的促进作用最小；高科等[12]通过实验和模拟相结合的方法，证实了瓦斯爆炸过程中爆炸冲击波及高温耦合能够引起二次瓦斯爆炸。国外方面，Ibrahim等[13]对障碍物与瓦斯爆炸相互关系进行了研究，分析了障碍物的大小、阻塞率以及泄爆压力对瓦斯爆炸超压值的具体影响；Salzano等[4]运用数值模拟和实验相结合的方法发现阻塞比不同、管道截面积变化率不同对可燃气体产生的扰动作用以及对气体燃烧的促进作用也不尽相同；Huld，Chang等[14-15]运用数值模拟的方法，证明了障碍物对瓦斯爆炸的过程确实存在激励效应。

许多专家学者已经对无通风状态的单条管路或简单分叉管路中的瓦斯爆炸传播规律进行了大量研究，并取得了重要成果，研究发现障碍物以及模型尺寸对瓦斯爆炸传播规律存在重要影响，但对大尺寸通风管网中的瓦斯爆炸传播研究极少。因此，有必要对障碍物在大尺寸通风管网模型中对瓦斯爆炸传播规律的影响开展相关研究，以便为更加贴近实际矿井结构和工况的瓦斯爆炸研究提供参考。本文利用Fluent对具有不同数量障碍物的大尺寸通风管网模型中瓦斯爆炸冲击波传播规律展开模拟研究，分析通风管网中障碍物对爆炸冲击波传播的影响。以通风管网中障碍物存在的管道为主要研究对象，通过对比分析该管道中各个监测点的超压变化曲线以及障碍物附近的速度矢量图，分析总结一般规律。

1 瓦斯爆炸在通风管网中的传播模型

1.1 基本假设

为了将问题简化，便于进行数值模拟，本文对瓦斯爆炸过程进行了以下合理假设与简化：

1)可燃气体爆炸过程为单向化学反应，属于不可逆过程；

2)爆炸开始前，爆炸腔体内可燃气体与空气均匀混合，初始状态为常温常压；

4)混合气体的比热容遵循随温度变化而变化的混合规则；

5)管道是刚性绝热壁面，不产生相对位移，不考虑容器与外界(包括壁面)的能量交换。

1.2 控制方程及方法

瓦斯爆炸数值模拟在二维笛卡尔坐标系下要同时依赖时间变量t和空间变量x，y，涉及到的控制方程包括质量守恒方程、动量守恒方程、能量守恒方程和组分质量守恒方程[16-17]。

本文在数值模拟中选用二阶迎风格式，双精度，压力基求解器和改进的PISO算法，燃烧模型选择组分输运模型，反应速率模型选择EDM模型，湍流模型选择RNGk-ε模型，采用非平衡壁面方程。

2 几何模型建立及网格划分

2.1 几何模型及监测点布置

本文中模拟的管道截面为正方形，形状比较规则，且属于轴对称，截面已经可以反映整个管道的瓦斯爆炸过程；三维模型计算周期较长，对计算机的性能要求较高，二维模型计算占用内存较少，对计算机性能要求较低，计算周期较短，计算结果也可精确地反应爆炸过程。管网模型长50 m，宽30 m，相关几何模型、监测点的布置及相关坐标见图1和图2。本文中选用条形障碍物，障碍物长1 m，宽0.2 m，障碍物所在管道宽2.5 m，阻塞比为40%。

2.2 网格划分

利用Gambit建模软件进行几何建模和网格划分，考虑到管道的形状和计算的需求，选择非结构三角形网格和结构四边形网格相结合对整个区域进行网格划分。障碍物处附近的网格划分如图3所示，有障碍物的模型划分了49 800个网格。无障碍物管网模型的网格划分如图4所示，无障碍物模型划分了49 850个网格。

2.3 边界条件和初始条件

对比分析文献[1,2,5,7,8]以及相关瓦斯爆炸数值模拟研究中边界条件和初始条件的设置，结合本文通风管网的特殊条件，设置边界条件和初始条件如下：

1)边界条件

1.2.2 实验分组 将大鼠按照随机数字法分为非糖尿病组(22只)和糖尿病组(22只),其中非糖尿病组大鼠采用随机字母法分为ZT23亚组(11只)、ZT11亚组(11只)；糖尿病组大鼠分为ZT23亚组(11只)、ZT11亚组(11只)。所有大鼠在制备模型中饲养4周，随后分别在ZT23和ZT11时间点，用戊巴比妥麻醉后，迅速打开胸腔，取出心脏。取材时间点设计参照文献[6-10]。

管网设有2个开口端，操作压力值为1个大气压，设定出口的组分为氧气23%，氮气77%，压力入口和压力出口的湍流强度均设为5%。壁面的粗糙常数为0.5，粗糙度厚度为0.1 mm。

图1 管网模型及监测点设置Fig.1 Network model and part monitoring point setting

图2 障碍物处模型及部分监测点设置Fig.2 The model of the obstacle and the setting of some monitoring points

图3 障碍物附近网格划分Fig.3 Grid partition near obstacles

图4 无障碍物管网模型网格划分Fig.4 Grid division of barrier free network

2)初始条件

本文采用浓度为9.5%的CH4-空气混合气体。

图1中标注了瓦斯填充区，尺寸为7 m×4 m，瓦斯充填区域内(除点火区外)的初始条件为：初始温度T0=300 K；气体中各组分的初始浓度分别为wCH4=0.053；wO2=0.21；wH2O=0；wCO2=0；wN2=0.737。

一般空气区的初始操作条件为：初始温度T0=300 K；气体中各组分的初始浓度分别为wCH4=0；wO2=0.23；wH2O=0；wCO2=0；wN2=0.77。

模拟中，原始爆炸点设置为已燃区(高温、高压的区域)，假设氧化反应完全，初始条件为：P0=2.5×105Pa；T0=1 600 K；wO2=0；wH2O=0.145；wCO2=0.118；wN2=0.737。

管网入口初始条件为：P0=2 500 Pa。管网出口采用压力出口。

设置时间步长为0.001 s(即1 ms)。

3 通风管网内冲击波传播模拟结果及分析

3.1 无障碍物时冲击波模拟结果及分析

无障碍物时底部直管中各个监测点的超压变化如图5所示。

图5 无障碍物时底部直管中各个监测点的超压变化Fig.5 Overpressure curve of each monitoring point in bottom straight pipe without obstacles

结合图1和图5可知：从监测点1到监测点2，由于管道截面积的突扩，使得冲击波超压降低速率减小；从监测点2到监测点40，由于该管道右侧存在压力聚集现象，使得超压降低速率变缓。该管道中监测点的超压整体表现出距爆炸源越近超压越大的规律。从爆炸开始到管道截面积突缩前，冲击波超压呈上升再下降的变化趋势。这与文献[3]中所述冲击波超压的变化规律相似。存在差异的原因是：文献[3]中的实验装置为密闭管道，冲击波碰到壁面反射与后续冲击波相互叠加的结果造成管段中出现的压力峰值反复波动，而本文中的通风管网模型入口和出口与外界都是连通的，未出现此反复波动现象。

底部直管右端90°拐弯处两侧监测点超压变化如图6所示。

图6 底部直管右端90°拐弯处两侧监测点超压变化Fig.6 Overpressure curve of monitoring points on the both sides of 90° turnt at the right end of the bottom straight pipe

由图6可知，在时间t分别为0.001，1.588，1.606和1.683 s时，相同时刻监测点40的超压明显大于监测点26处的超压。出现这个现象的原因是：爆炸冲击波从监测点40所在管道一侧传入监测点26所在管道时，管道截面积突缩产生阻碍，造成监测点40附近压力的聚集，冲击波开始压缩底部直管右侧的气体形成压缩波。与参考文献[6]对瓦斯爆炸在拐弯管道中的传播(拐弯管道/开口)论述相比，虽然在拐弯前后2个监测点的超压值上存在偏差，但是冲击波通过90°拐角时的超压衰减系数K(K=P40/P26)都在1.1～1.2之间。

3.2 单个障碍物时冲击波模拟结果及分析

底部直管中各个监测点的超压变化如图7所示。

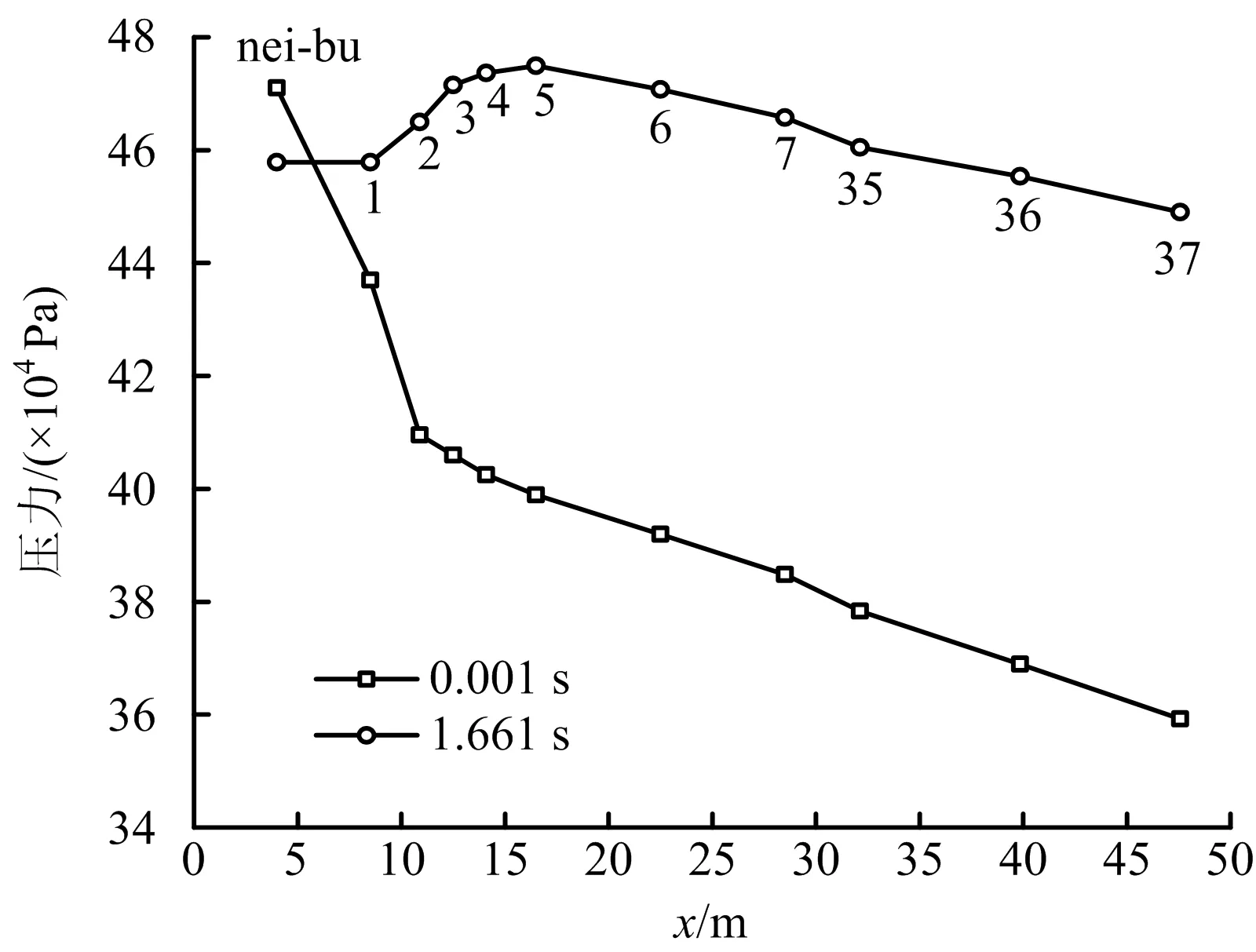
图7 有障碍物时底部直管中各个监测点的超压变化Fig.7 Overpressure curve of each monitoring point in bottom straight pipe with obstacles

由图7可知，t为0.001 s时，冲击波超压从监测点nei-bu到监测点2快速降低，其后方监测点的超压降低速度明显减慢，该现象及其出现的原因与无障碍物模型基本一致，主要是由管道截面积突缩和压力集聚造成的。时间为1.661 s时，从监测点nei-bu处到监测点5处，超压呈增加的趋势；监测点5之后，该管内各个监测点的超压呈减小趋势。初期爆炸中，冲击波传播路径以及叠加区域变化对涌出腔体的大量未燃瓦斯气体的积聚区域产生影响。对比相应监测点的超压数值发现，障碍物的存在使得二次瓦斯爆炸更加剧烈。

障碍物附近监测点的超压变化如图8所示。

图8 障碍物附近监测点的超压变化Fig.8 Overpressure curve of monitoring point near obstacle

由图8可知，在t分别为0.001和1.661 s时，监测点7处的超压都要稍高于监测点35处的超压。冲击波传播的过程中，虽然能在障碍物处形成强烈的湍流，与高温气团形成正反馈机制，但是这个过程中障碍物的阻碍作用占主导，障碍物削减了爆炸波的强度，使障碍物后超压减小。同时，障碍物的存在使得二次爆炸在该处形成的超压要远大于初期爆炸。这与文献[9]中“障碍物的存在使冲击波超压增大”的论述相同。

图9为障碍物附近不同时刻的局部速度矢量图。

图9 障碍物附近不同时刻的局部速度矢量图Fig.9 Local velocity vector near the obstacles at different time points

由图9可知，t为0.001 s时，障碍物的存在减小了传播速度，阻碍了冲击波的传播，但障碍物前后没有形成明显的涡团；t为1.661 s时，障碍物附近不仅速度值增大了而且障碍物后有明显的涡团形成。障碍物的存在使得冲击波在绕过障碍物传播的过程中产生了湍流现象，这与文献[8]中的论述相同。被障碍物阻挡的一部分冲击波，绕过障碍物进入障碍物后的涡团后继续向前传播，冲击波强度减弱。

底部直管右端90°拐弯处两侧监测点超压变化如图10所示。

图10 底部直管右端90°拐弯处两侧监测点超压变化Fig.10 Overpressure curve of monitoring points on the both sides of 90° turnt at the right end of the bottom straight pipe

由图10可知，在只有1个障碍物存在时，在底部直管的右端拐弯处,位于底部直管一侧的监测点37处的超压要高于位于出气管侧监测点26处的超压。此结果类同于无障碍物模型中底部直管右端出现的压力聚集现象，与文献[6]对瓦斯爆炸在拐弯管道中的传播(拐弯管道/开口)论述类似。同时，该现象阻碍了火焰波在底部直管中的传播，大幅减弱了障碍物附近冲击波与火焰波正反馈机制。

通过对比分析通风管网内瓦斯爆炸的3个时期(即初期爆炸时期、二次瓦斯爆炸时期和通风动力系统恢复时期)冲击波的传播规律。障碍物通过影响初期爆炸冲击波的传播，进而改变了流入到管网中的未燃瓦斯气体的分布与积聚位置；在二次爆炸后，不同管道中的冲击波发生复合作用(冲击波与冲击波、冲击波与火焰波以及冲击波与障碍物相互作用)产生的高压区域，相对无障碍物时压力较高，而且高压区的位置相对无障碍物时也发生了改变。在有障碍物时，各监测点超压峰值出现的次数也相对减少，但超压值却增加，说明障碍物的存在会使冲击波的强度相对增强，冲击波、火焰波复合作用的次数相对减少。通过分析有障碍物的模拟结果发现：障碍物的存在虽然在一定程度上减小了初期爆炸阶段冲击波的强度，但障碍物的存在改变了初期冲击波复合作用区域，进而改变了随冲击波一同传入管网的未燃瓦斯气体的分布和积聚位置，对管网内发生的二次瓦斯爆炸影响甚大。由于管网的2个开口端处于开放状态，增加了冲击波传播的复杂性。

4 结论

1)障碍物通过影响初期爆炸中冲击波的传播路径和叠加区域的位置，进而改变未燃瓦斯气体在管网中的积聚，从而对二次瓦斯爆炸中冲击波的强度、复合作用区域、高压区域产生影响。

2)在二次爆炸中，不同管道中的冲击波发生复合作用而产生的高压区域相对于无障碍物时压力更高，而且高压区的位置相对无障碍物时也发生了改变。

3)通过对比2个模型的模拟结果发现，冲击波在通过障碍物后都会形成涡团，加大了湍流强度，进而与火焰波形成正反馈机制，增加了冲击波能量补充，使其在开放式通风管网内的传播更加复杂。

4)实际矿井生产中，应当尽量避免障碍物的存在；障碍物无法避免时，应该合理分布障碍物的位置。