路径-脆弱点最短距离最大化的危险品运输网络设计*

项 寅, 姜冠群

(上海财经大学 商学院，上海 200433)

0 引言

危险品交通运输事故容易造成重大人员财产损失，因此如何降低危险品运输风险，受到了学术界的大量关注和广泛研究。相关研究以危险品运输风险评估[1-3]为起点，逐步拓展到危险品运输路径优化[4-5]、网络设计[6-8]、应急设施选址[9]，以及恐怖袭击下的危险品运输优化问题[10]。其中，网络设计和风险评估与本文紧密相关。

目前，危险品运输网络设计思路大体包括2类。第1类思路采用关闭路段的方法来禁止危险品车辆行驶于覆盖人口较多的路段之上，以此降低车辆路径的风险，该方法首先由Kara和Verter提出[6]，主要针对静态网络展开研究并利用双层理论构建模型；后续学者则进一步考虑了运输风险和行驶路径之间的折中方案选择[8]、网络设计中的分流站点选址规划[11]，以及随机和时变情形下的危险品运输网络设计[12-13]。第2类思路则通过征收过路费的方式来控制和约束危险品车辆的行驶路径，Marcotte等是该方法的提出者[14]，相关拓展研究进一步考虑了承运商的路径偏好[15]及其在铁路网络中的应用[16]。

现有危险品运输风险的计算方法主要包括事故率风险模型[1]、传统风险模型[2]、条件风险模型[3]、人口覆盖率风险模型[17]等。这些风险模型从事故率、事故后果、人口分布这3个角度来实现风险度量，而目前的危险品运输网络设计研究则较多采用了人口覆盖率风险。

通过文献综述发现：现有危险品运输网络设计仍有2方面不足，一方面是常用的人口覆盖率风险忽略了脆弱点和距离这2类因素，此处脆弱点是指分布在道路两旁的人口集聚且难以快速疏散的场所，例如，当某路段周围脆弱点的人口分布较多，但是分布人群离开该路段的距离较远时，其风险可能小于另一条周围人口分布较少，但人群距离较近的路段；另一方面是现有研究大多以最小化运输风险为决策目标，通过压缩承运商经济利润来降低风险，而关于兼顾风险-成本的优化模型及算法则仍然有待完善。

本文将Bronfman等[18]提出的1类危险品道路风险评估方法引入危险品运输网络设计研究中，通过脆弱点和运输路径间的加权距离来度量风险，实现人口分布和距离这2类风险影响因素的联合考虑；设计1类启发式算法，该算法结合具体算例可在多项式时间内获取最优解、次优解、…、第k优解，为寻求兼顾运输风险和运输成本的优化方案提供决策支持。

1 基本分析

本文主要考虑的危险品种类为发生泄漏事故后可产生大面积扩散的有毒气体，如液氯等。一旦此类事故发生，道路两旁的脆弱点(如医院、学校、购物中心、居民区等)中往往集聚着大量人群，其不易在短时间内疏散，故很容易因有毒气体的扩散而受到危害。在有毒气体参数和气象环境给定的情况下，对应浓度及危害程度往往和相离事故点的距离紧密相关。在该情景下，由于传统风险评估方法[1-3,17]无法着重反映脆弱点和距离等实际因素，因此本文参考文献[18]并将危险品运输路径和各脆弱点间的加权距离作为风险界定方法，加权距离越小，风险系数越大。

危险品运输网络设计所需解决的问题为：给定某交通拓扑网络，在各路段的周围分布着一些医院、学校、公园景点、购物中心之类的“脆弱点”，且每个脆弱点存在1个权重，反映为该地点的人口数量。承运商选择源汇点间的最短路径来实现危险品的运输，政府则需通过关闭网络中的部分路段，来控制和约束承运商的运输路径，并使之最大程度地远离各脆弱点，即最小化运输风险。

与经典危险品运输网络设计问题[6]相同，上述问题同样是1个典型的双层规划问题。如图1所示，政府处于领导地位，其决策属于上层规划，通过关闭交通网络中的一些路段来最大化危险品运输路径和各脆弱点间的最小加权距离；承运商处于从属地位，其决策属于下层规划，需在政府给定的危险品运输网络下，决策源汇点间的最短路径，以最小化其运输成本。

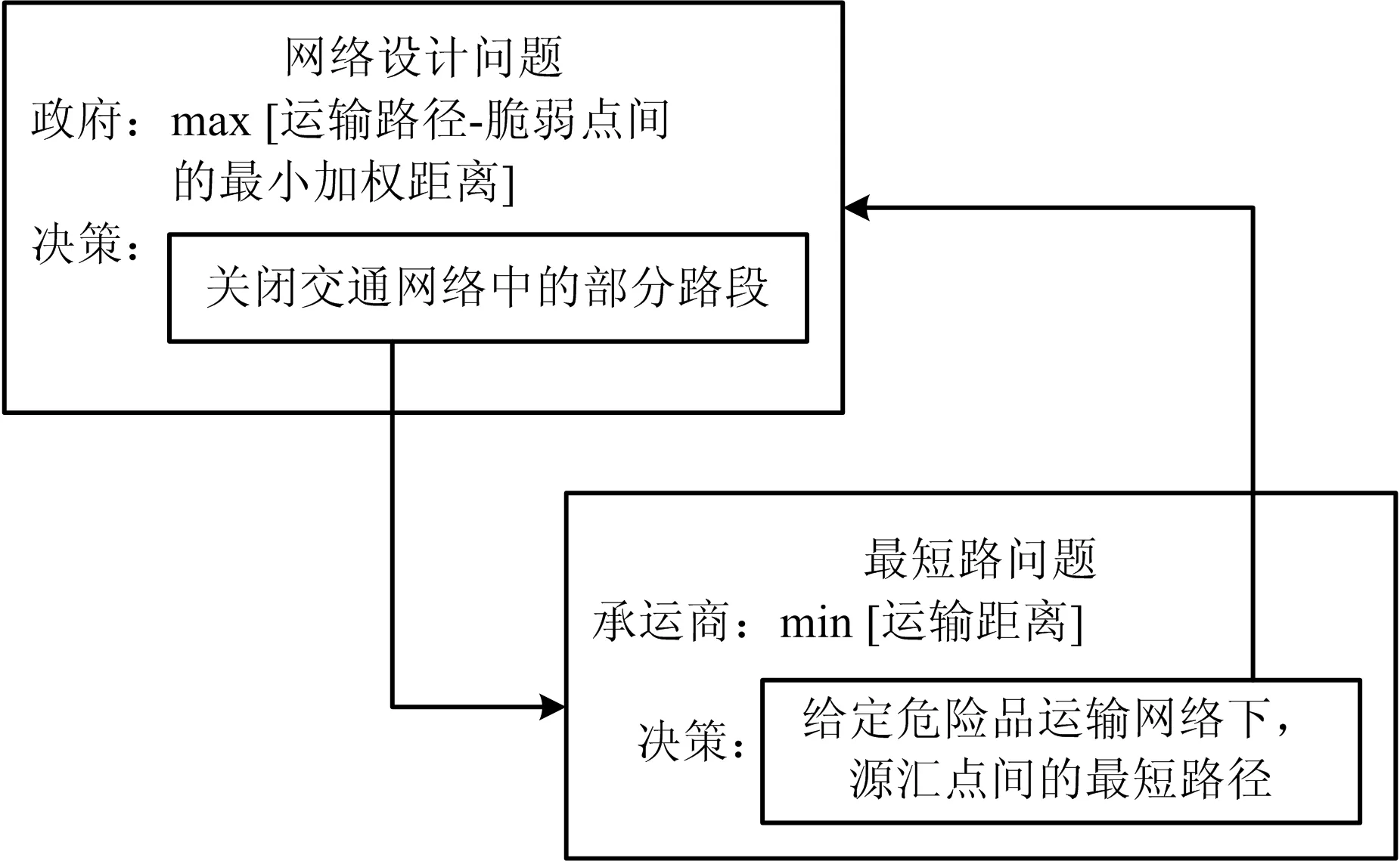
图1 双层规划模型结构示意Fig.1 Structure of the bi-level programming model

2 问题描述

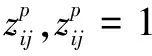
3 数学模型

将上述问题构建为如下双层规划模型：

(1)

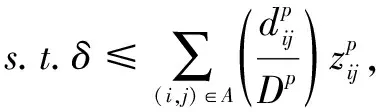
(2)

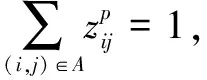
(3)

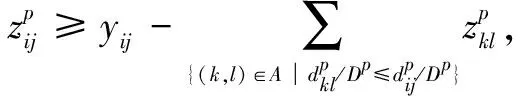
(4)

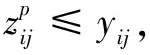
(5)

xij∈{0,1},∀(i,j)∈A

(6)

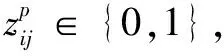
(7)

其中，yij为下层规划的解

(8)

(9)

yij≤xij,∀(i,j)∈A

(10)

yij∈{0,1},(i,j)∈A

(11)

式(1)～(7)是关于政府的危险品运输网络设计问题，式(8)～(11)则是承运商在给定危险品运输网络下的最短路径决策问题。

上层规划中，目标式(1)表示最大化路径和脆弱点间的最小加权距离δ；而约束式(2)保证了δ一定是危险品运输路径与所有脆弱点间的最小加权距离；约束式(3)确保分配给脆弱点p的加权距离最小的路段是唯一的；约束式(4)为最近指派约束，保证分配给脆弱点p的路段一定是离开其加权距离最小的；约束式(5)确保被分配的路段必须为承运商的通行路段。下层规划中，目标式(8)表示最小化危险品运输路径的总距离；约束式(9)为流量平衡约束，保证承运商选择的各通行路段可以合并为源汇点间的一条连通路径；约束式(10)限制承运商只能选择开放的路段行驶。

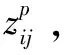
4 算法设计

双层规划是典型的NP-难题。为求解上述危险品运输网络设计模型，本文设计1类启发式算法。

4.1 符号说明

4.2 算法思路

该启发式算法包括2个阶段。

1)第1阶段：确定风险最小，即离开所有脆弱点的最小加权距离最大的路径。按θij从小到大，即风险由高到低的顺序，依次对各路段(i,j)关闭，每次迭代仅关闭1条路段并逐步累加。每次迭代移除关闭路段后，用dijkstra算法求解源汇点间的最短路径，若路径存在，进入下1次迭代，若路径不存在或网络不联通时，停止迭代并将前1次迭代所得路径作为风险最小的运输路径。

2)第2阶段：修正第1阶段的路段关闭方案。由于第1阶段采用贪心法逐一关闭路段，故会产生一些“无效”方案。在所有被关闭路段中，按θij从大到小，即风险由低到高的顺序依次进行开放，每次迭代仅开放1条路段并逐步累加。每次迭代开放相应路段后，用dijkstra算法求解源汇点间的最短路径，若该路径和第1阶段得到的最小风险路径相同，说明开放当前路段不增加风险，开放该路段并进入下1次迭代；若2条路径不同，说明开放当前路段会增加风险，则仍然保持该路段的关闭状态，并进入下1次迭代。直到所有在第1阶段中被关闭的路段都得到1次“开放测试”后，所保留下的被关闭的路段就为政府最优的路段关闭方案。

4.3 算法步骤

启发式算法的具体步骤如下：

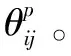
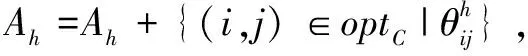
4)步骤4：最优解确定。得到optC为政府最优的路段关闭方案，相应的承运商行驶路径则为optR。

4.4 算法性质

1)性质1：算法是收敛的，且路段关闭方案optC下的危险品运输路径optR一定为风险最小的路径，即离开所有脆弱点的最小加权距离最大的路径。

证明：由步骤2看出，随着迭代的进行，交通网络中的路段按照其与所有脆弱点加权距离θij由小到大的顺序依次被关闭。那么，在剩余的开放路段中，路径R和所有脆弱点间最小加权距离θR的下界会不断增加，并等于剩余开放路段中最小的θij值，又由于每次迭代都是在上1次迭代的基础上，继续关闭1条θij最小的路段，因此上述加权距离θR的值会不断增加。显然，有限数量的迭代后，随着关闭路段数量的增加，网络不再连通，此时算法停止，且θR收敛到最大的1个值。

2)性质2：算法的计算时间复杂性为O(2|A||N|2)。

证明：显然，整个算法的主要计算时间复杂性存在于步骤2～3中的迭代过程。

首先，用dijkstra算法计算2点间最短路径的计算时间复杂性为O(|N|2)。

其次，步骤中最坏的情况是依次关闭|A|-1条路段，即进行|A|-1次迭代，而每次迭代最主要的计算时间成本在于dijkstra算法的执行。

最后，步骤3中最坏的情况需依次开放|A|-1条之前被关闭的路段，即进行|A|-1次迭代，而每次迭代最主要的计算时间成本同样为dijkstra算法。

综上所述：算法的计算时间复杂性就为O(2·(|A|-1)·|N|2)～O(2|A||N|2)。

4.5 算法拓展

改进算法第1阶段，不再要求达到网络不连通或最短路径不存在时才停止迭代，而是要求当前迭代所得路径和上次迭代所得路径不同时进入第2阶段的修复过程。这样，第1阶段就记录下了各类风险值下的运输路径，第2阶段通过修正就进一步得到风险最大、次大、第k大路径所对应的路段关闭方案。具体应用将在算例分析部分展示。

5 算例分析

5.1 算例描述

本文以包含20个节点、31条边和10个脆弱点的拓扑网络为例进行算例分析，如图2所示。其中，节点2和节点18分别为承运商的起点O和终点D。各脆弱点p的人口权重Dp如表1所示，每个脆弱点表示为不同灰度的圆，将脆弱点的坐标定义为圆的中心位置，用其半径来表示该脆弱点到临近路段的最小欧式距离，而其着色深度和表示符号则对应了不同大小范围的人口权重。每条边(i,j)的长度lij及各边和所有脆弱点间的最小加权距离θij如表2所示。

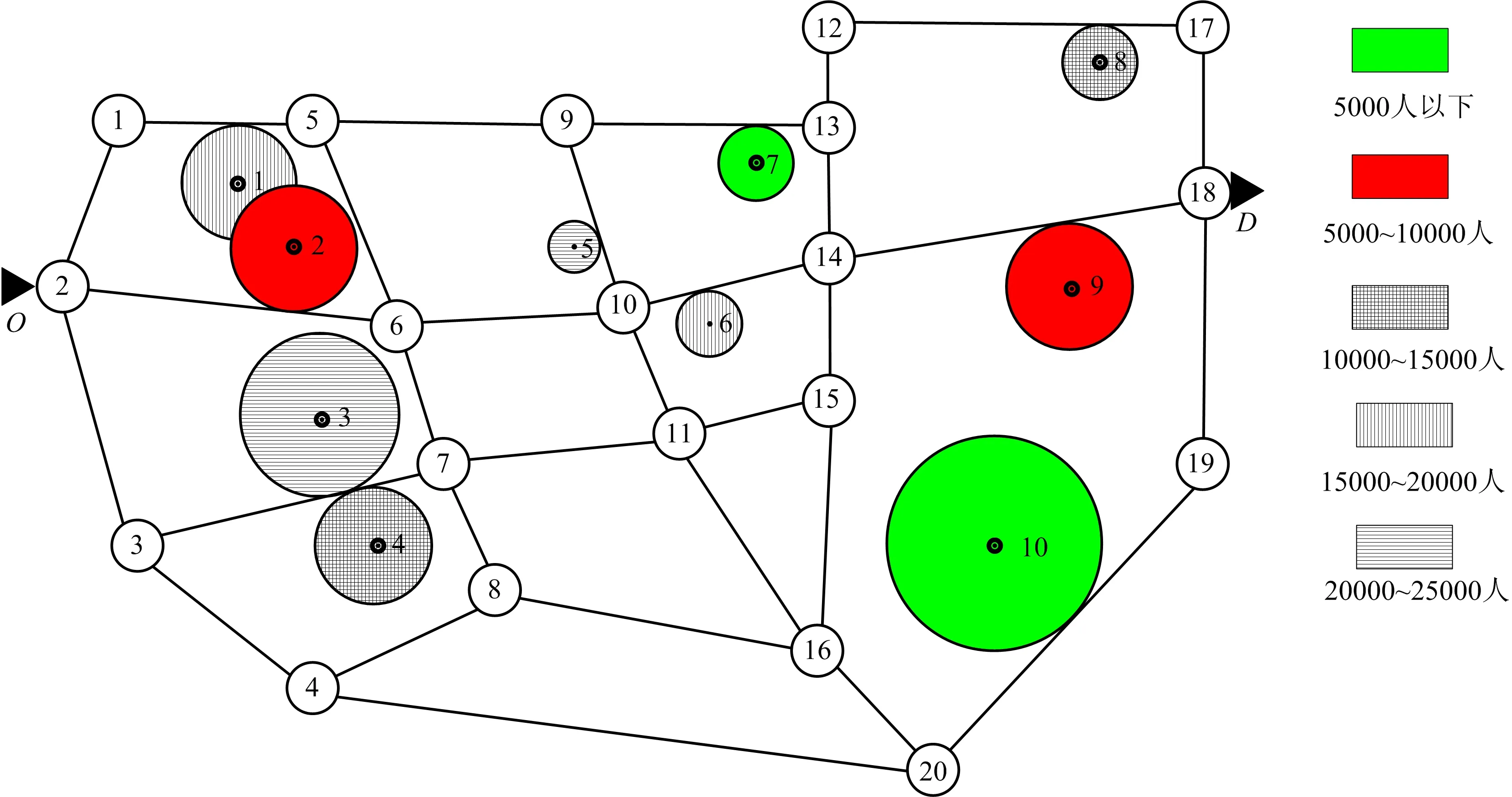
图2 20个节点的拓扑网络Fig.2 A topological network with 20 nodes

p12345678910Dp1682411201541192

在实际应用中，脆弱点的中心位置通常可取作医院、学校等设施的坐标中心位置，而脆弱点的人口权重则可近似为对应场所的常住人口数、日客流量等。

5.2 计算过程演示

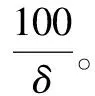
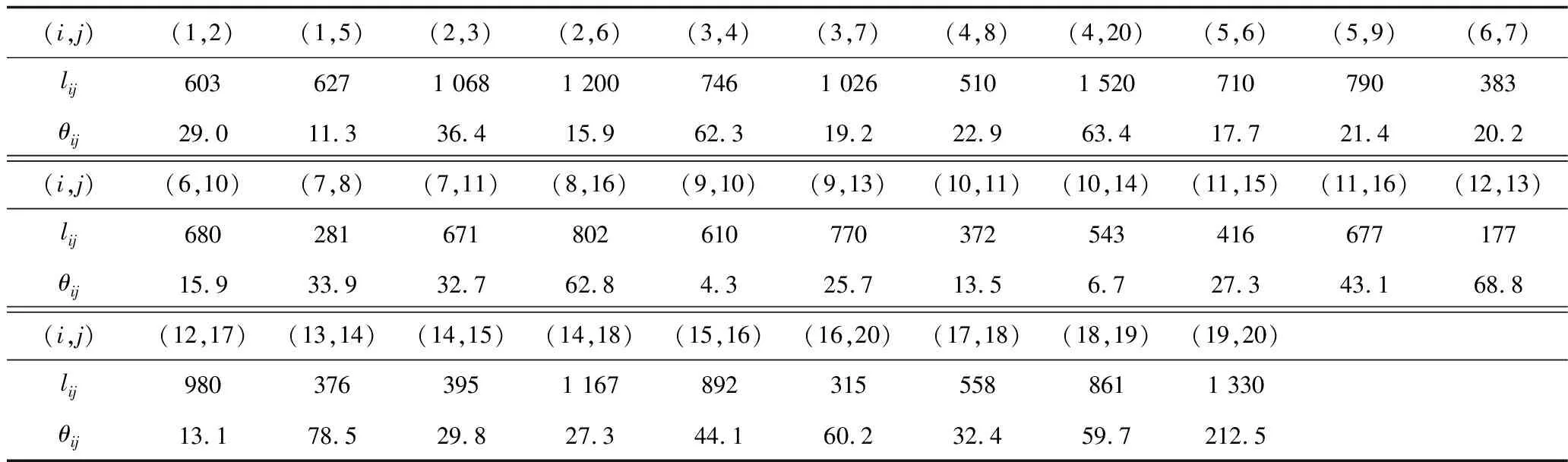
表2 各路段的长度及其距所有脆弱点的最小加权距离Table 2 Length of all road segments and their weighted distance from all vulnerable zones

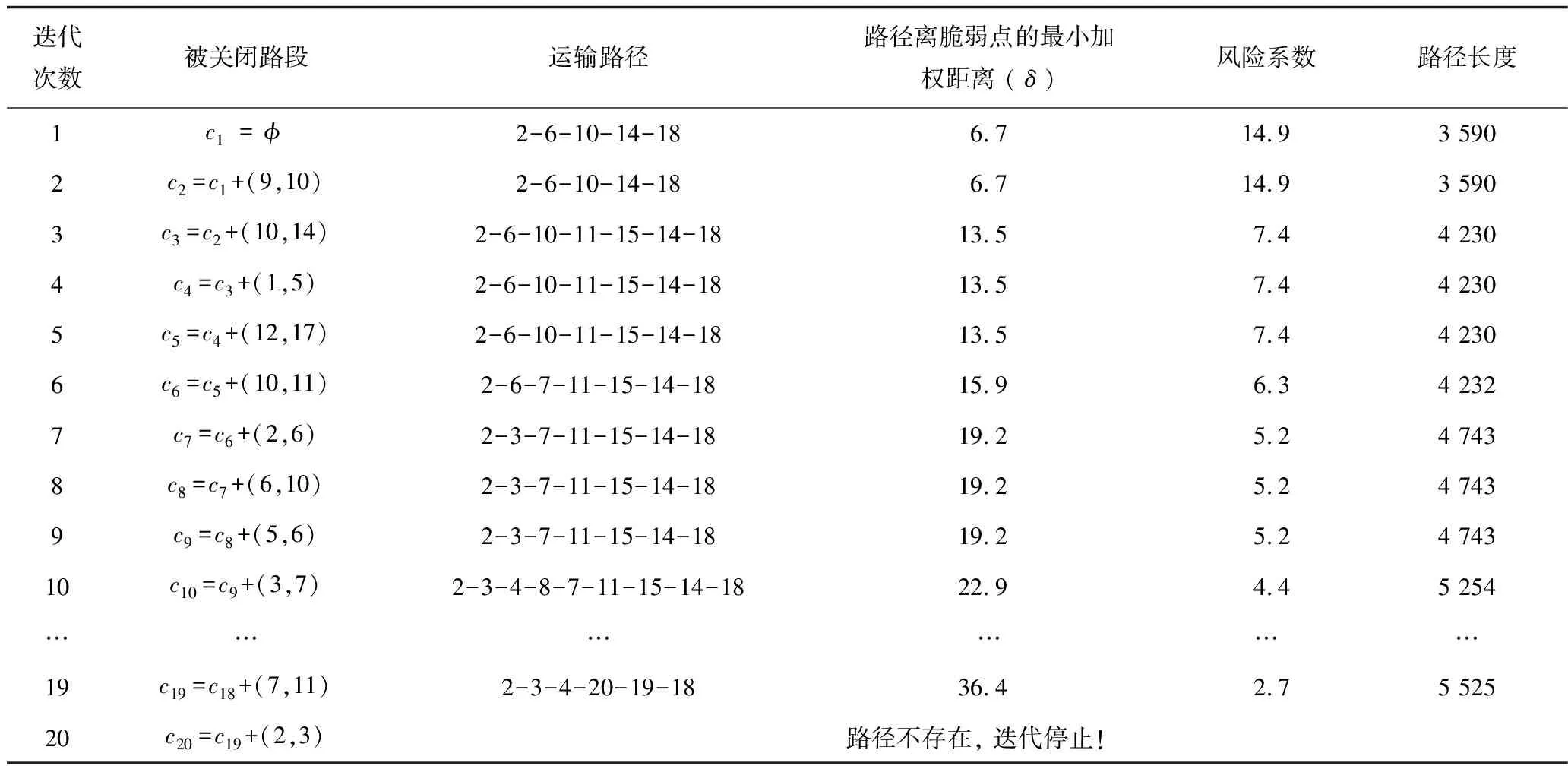
表3 启发式算法第1阶段迭代过程Table 3 The first stage iteration process of heuristic algorithm

随着迭代次数的增加，政府关闭的路段数不断增多，承运商的运输路径发生改变，路径的风险系数逐渐降低但路径长度不断变长。当进行到第3,6,7,10,19次迭代时，分别产生了风险最大的、次大的……第5大的路径方案及对应的路段关闭方案。直到第20次迭代，源点和汇点间不存在开放的路径，此时算法第1阶段计算停止，将第19次迭代所得到的路径2-3-4-20-19-18作为风险系数最小的路径，并转入第2阶段计算。

算法第2阶段针对第1阶段第19次迭代中所有关闭的18条路段逐一进行“开放”测试，如果开放后的运输路径与开放前一致，则开放该路段，否则仍保留关闭状态，迭代信息如表4所示。

如表4所示，当算法第2阶段进行到第7,10,13,16次迭代时，开放测试路段会改变原有路径并减少路径和脆弱点间的最小加权距离，因此仍然保留路段(4,8)(3,7)(2,6)(1,5)的关闭状态，并得到了运输路径风险系数为最小值2.7时的政府路段关闭方案。

结合表3～4发现，算法经过38次迭代后即收敛至最优解，验证了4.4节性质1的正确性，且对应4.4节性质2，每次迭代仅需计算新增“被关闭路段”或“被开放路段”后的最短路径，其计算时间成本与脆弱点个数无关，且计算时间复杂性满足多项式函数形式。

5.3 最优决策

同理，根据表3依次选择在第3次、第6次、第7次、第10次迭代时停止算法第1阶段计算并转入第2阶段，进而可得到风险系数分别为7.4、6.3、5.2和4.4时的运输路径及对应的路段关闭方案。汇总整理所有可行方案并记录于表5。

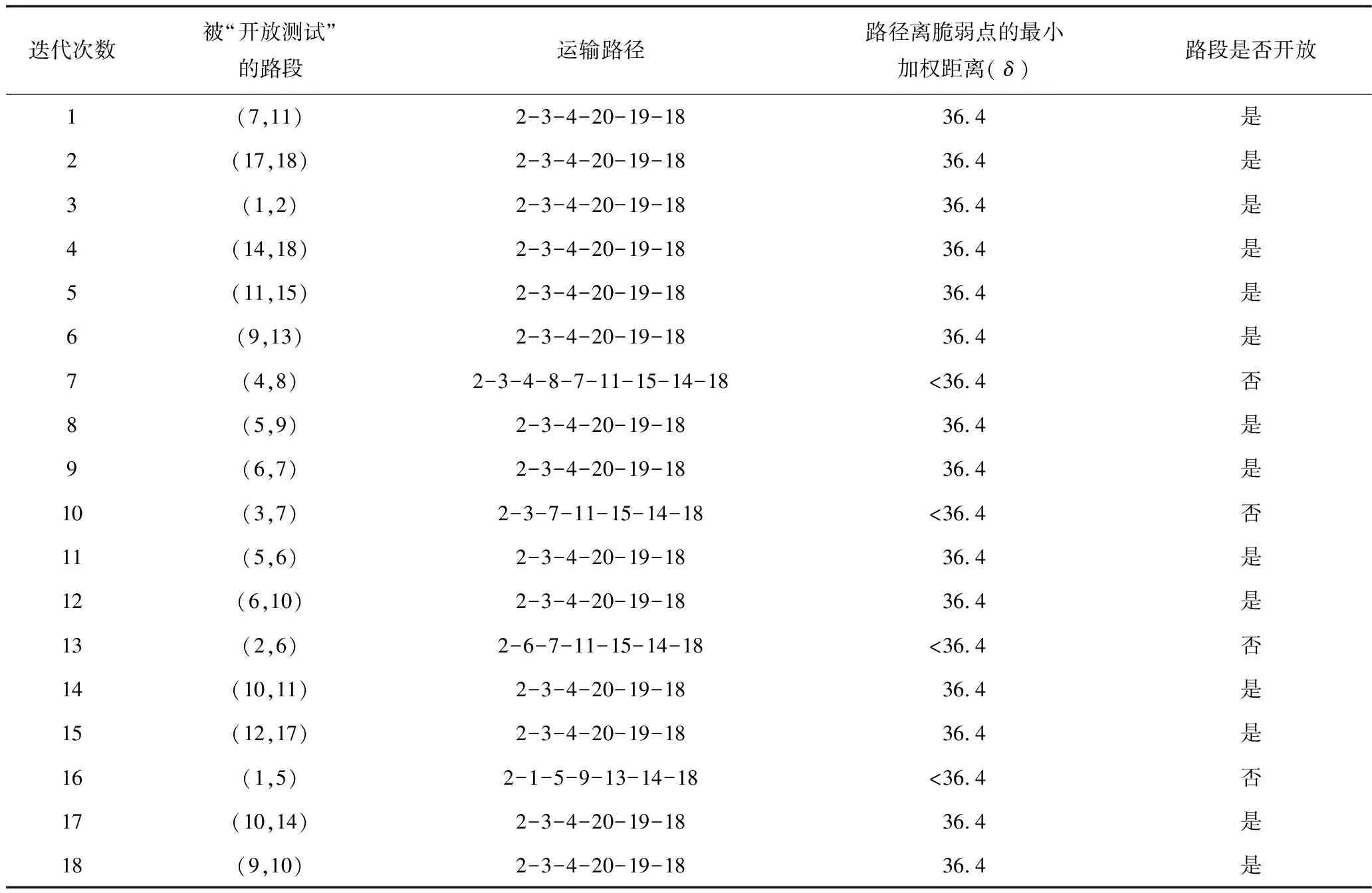
表4 启发式算法第2阶段迭代过程Table 4 The second stage iteration process of heuristic algorithm

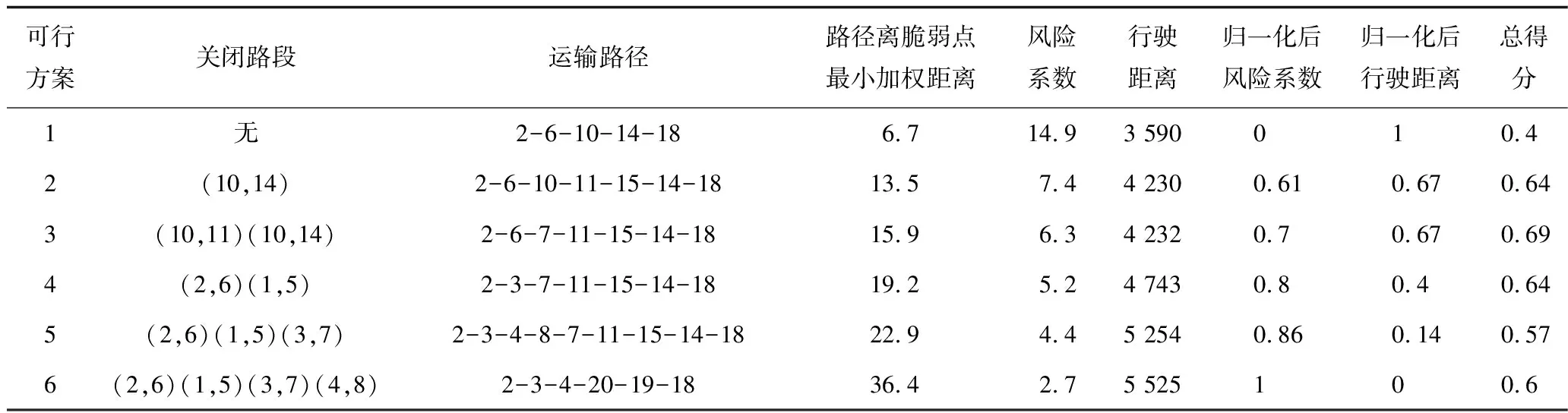
表5 可行方案及其加权评分Table 5 Summary of all feasible solutions and their weighted score

表5包含6类可行方案，随着序号的上升，对应方案下的风险系数不断下降但行驶距离逐渐增加。为寻求兼顾运输风险和运输成本之间的最优方案，政府可通过加权评分法来实现最终决策。首先，对风险系数和行驶距离数据进行归一化处理并用于消除量纲；其次，结合实际情况分配权重，例如分配给风险系数的权重为0.6而行驶距离的权重为0.4；最后，对表中的第7列和第8列数据进行加权求和，并选择总得分最高的方案。本算例中，由于方案3的总得分最高，因此该方案最终入选。

6 结论

1)针对已有危险品运输网络设计问题进行拓展，考虑1类新的风险评估方法，通过计算路径和脆弱点间的最短加权距离来评估路径风险系数，兼顾路径两侧的人口因素和脆弱点的距离因素。利用双层理论构建模型，并设计启发式算法求解。

2)通过算例分析发现：该启发式算法经过有限次数的迭代即可获取风险系数最小、次小、第k小的路径及其对应的路段关闭方案，进一步利用加权评分法即可获取最优方案，为寻求兼顾运输风险和运输成本间的最优方案提供决策支持。

3)未来研究可考虑多源多汇的情形，并对启发式算法进行改进；可进阶考虑运输过程涉及多类危险品的情形，改进模型并对脆弱点设置不同的属性类别，以实现各类危险品运输的分类管理；也可针对行驶成本、脆弱点权重的随机或时变特征展开研究，提出随机/时变模型并更好地拟合现实情景。