页岩层理结构对超声波特性响应分析及应用

徐烽淋 ，陈乔 ，朱洪林，王丹，陈吉龙，刘璞，姚光华，张阔，霍振永

（1. 重庆市涪陵页岩气环保研发与技术服务中心，重庆 408000；2. 中国科学院重庆绿色智能技术研究院，重庆 400714；3. 油气藏地质及开发工程国家重点实验室，成都 610500；4. 重庆矿产资源资源开发有限公司，重庆 401120；5. 中国石油西南油气田公司蜀南气矿，四川泸州 646300）

0 引言

页岩复杂层理结构会导致岩石的超声波特性变得复杂，无法准确求取储集层的力学参数。Josh等[1]通过分析页岩气区块的相关资料发现，页岩复杂层理结构导致声波测井资料存在各向异性，Vernik等[2]、邓继新等[3]通过页岩波速的各向异性也得到类似的结论。Horne等[4]利用偶极子声波测井数据来判断层状页岩弹性各向异性，估算出各向异性参数与邻井预测值一致；张白红等[5]测量了2种岩块垂直和平行层理两个方向的超声波速，数据表明平行于层理面方向及其法线方向具有明显的波速各向异性。Yan等[6]、程礼军等[7-8]等分别研究页岩在单轴、三轴压缩条件下的波速变化，发现随着轴向载荷的增加，纵、横波速度呈先增后降的趋势。Chen等[9]、熊健等[10]和吴涛等[11]通过超声波透射实验发现，波速随层理角度的增加或频率的减小而减小；衰减系数随角度或频率的增加而增大，平行于层理方向的波速与层理密度呈线性正相关，而垂直于层理方向的波速与层理密度呈线性负相关。Schn等[12]基于超声波实验建立了页岩弹性性质的函数形式，并通过该函数计算速度和各向异性。

综上所述，国内外学者主要利用露头或者井下岩心制作不同层理结构的物理模型，通过超声波透射实验总结页岩声波特征响应的定性认识[13-14]。考虑到页岩制样困难，同时，由于实验研究对页岩的大量耗损导致无法开展大规模的物理模型实验，致使研究结果具有一定的局限性。针对上述问题，本文以页岩层理结构为研究对象，基于波动理论，对超声波透射实验过程进行数值模拟，计算页岩不同层理结构模型的超声波响应规律，利用灰色系统理论筛选对层理结构敏感的声学参数，进一步建立页岩的动态力学参数模型，研究结果对提高利用声波资料预测岩石力学参数的准确性具有重要意义。

1 数值模拟方法

1.1 波动理论

弹性理论主要研究物体受力与形变的关系，其波动方程由本构方程、运动平衡微分方程和几何方程共同建立。在弹性各向同性介质中，二维一阶速度-应力弹性波动方程为：

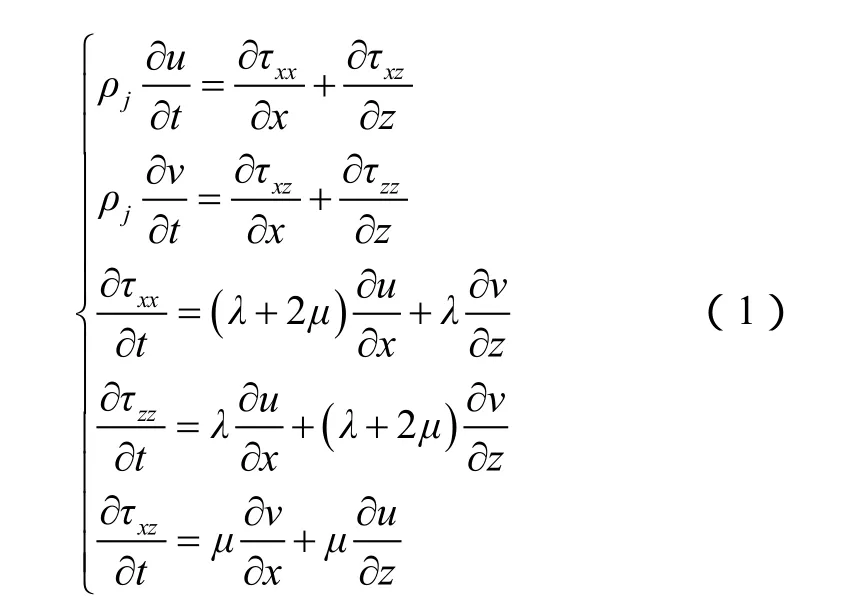
在时间上，采用二阶精度的时间差分方程解的近似值，在空间采用四阶差分方程解的近似值，利用交错网格格式，取

可推导出波动方程的差分格式：

1.2 波动方程求解

1.2.1 边界条件

在计算区域中左、右边界与实际条件基本相符，按照常规反射边界来处理，而上、下边界和 4个边角点设置吸收条件。

1.2.2 初始条件

当t≤0时，速度和位移为零，即

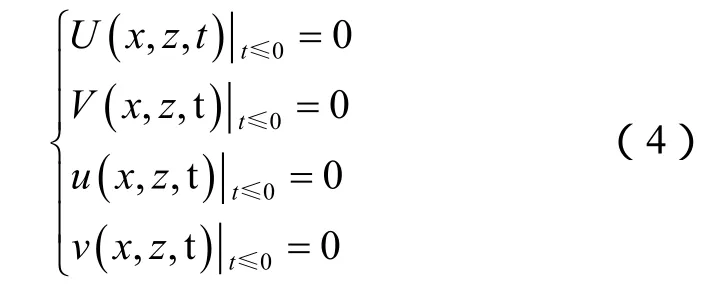
1.2.3 振源条件

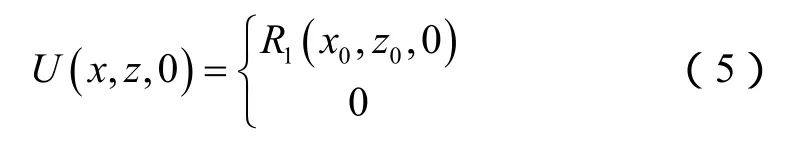
1.2.4 收敛条件

分析误差传播和积累的情况，是保证差分格式收敛性的基础。董良国等[15]详细推导了交错网格高阶差分方程的稳定性条件。当介质为均匀各向同性时，时间精度为二阶，空间精度为四阶的稳定条件为：

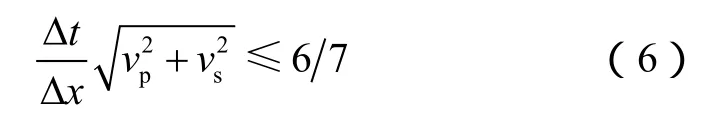
实验室超声波测试采用透射法进行测量。但由于页岩的非均质性及层理分布的不确定性，给研究层理结构对超声波传播特性的影响带来了较大困难，而且透射实验中岩心与探头接触不平整以及人为读取初始时间等也会造成误差。数值模拟基于被测岩心的纵向剖面建立模型，以超声波探头的激发信号为振源，基于波动理论推导出一阶位移-应力弹性波方程组，并开展交错网格半程计算，用Matlab编程实现超声波透射实验的模拟。

1.3 数值模拟验证

1.3.1 波形对比验证

为了使模型与超声波透射实验相统一，将探头频率设为250 kHz。其中入射波信号显示为初始波形，当入射信号透过岩心到达接收端时，实验室可获取透射信号，显示为实验波形，而数值计算的结果显示为模拟波形（见图1）。波形对比结果显示，模拟波形与实验波形到达接收端的时间均为0.9×10-5s左右，电压均为-5～5 V，二者范围相近（见图1）。

将模拟波形和实验波形进行相关性计算，将模拟波形信号设为X，实验波形信号设为Y：

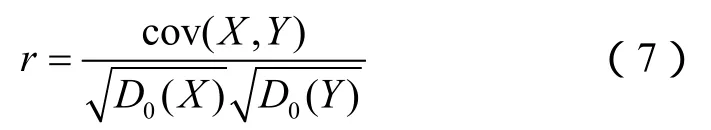
X和Y的标准差分别为：

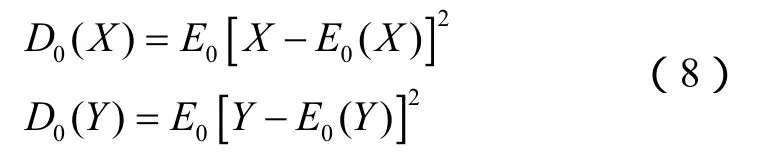
协方差：

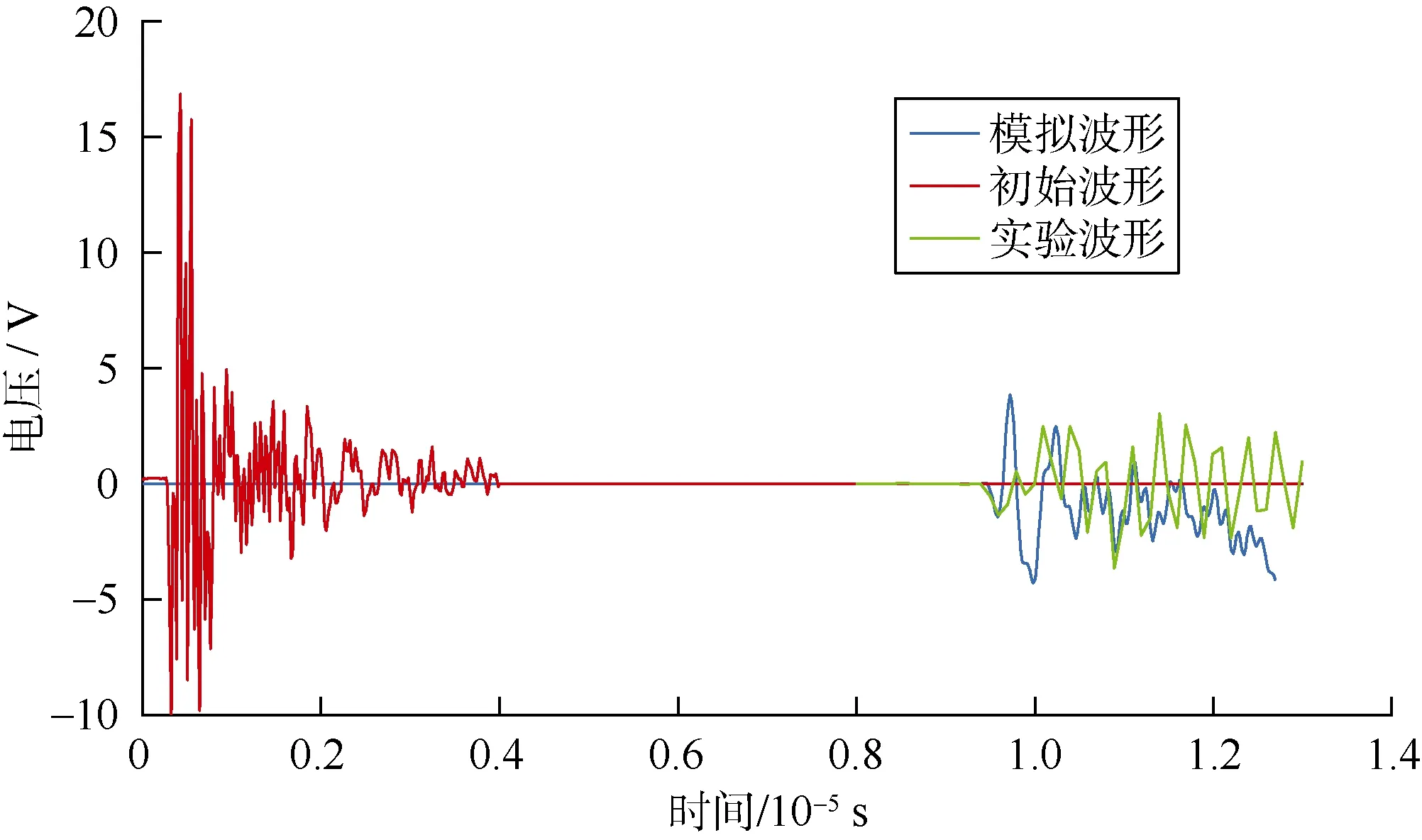
图1 标准页岩超声波透射实验与数值模拟结果对比图

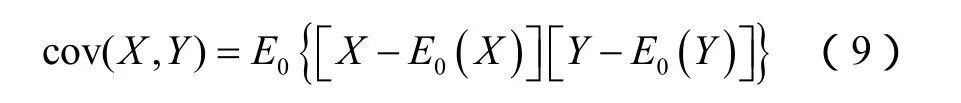
通过相关性计算得到模拟波形与实验波形之间的相关系数为 0.85，吻合度较高，所以该数值模拟方法可对超声波透射实验进行有效的模拟。

1.3.2 数值计算验证

考虑到层理角度为页岩最显著的结构特征，因此，结合实际岩心建立类似不同层理角度的理想岩心模型，在此基础上开展数值模拟计算。图2是渝东南地区下志留统龙马溪组露头岩心，编号记为A1、A2、A3、A4。层理角度为层理方向与超声波传播方向的夹角，其中 A1的层理角度为 0°，A2为 30°，A3为 60°，A4为 90°（见图2）。为了进一步验证数值模拟方法的有效性，本文还以A1、A2、A3、A4岩心为模板，建立数值模型B1、B2、B3、B4（见图3）。在模型中对速度参数进行设置，将超声波在层理中的速度值设置为1 900 m/s，将其在骨架中的速度值设置为4 200 m/s，该模型为理想的层理角度模型，其角度与岩心 A1、A2、A3、A4一一对应。在此基础上，对超声波透射实验与数值模拟结果进行对比验证。

图2 渝东南地区下志留统龙马溪组露头岩心照片（据参考文献[9]修改）

通过超声波透射实验完成对岩心A1、A2、A3、A4在不同探头频率条件下衰减系数的计算，结果显示，在同一层理角度下，随着探头频率的增大，衰减系数整体呈现出增大趋势（见图4a）。同时，通过数值模拟也完成了对模型B1、B2、B3、B4在相同条件下的计算（见图4b），数值模拟计算得到的规律与超声波透射实验规律基本吻合[16]，即在同一层理角度下，衰减系数与探头频率均呈正相关。

图3 渝东南地区龙马溪组岩心数值模型（据参考文献[9]修改）

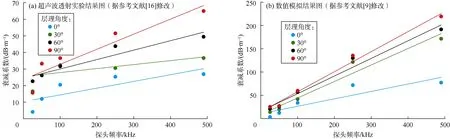
图4 超声波衰减特性结果对比图（样品数4个）

图5 渝东南地区下志留统龙马溪组露头岩心照片

图6 渝东南地区下志留统龙马溪组岩心层理提取结果图

上述数值计算是基于理想的层理角度模型。为了进一步验证上述数值模拟结果的可靠性，利用数值图像处理技术提取出真实岩心的层理角度，然后再开展不同层理角度的衰减系数数值计算。图5是渝东南地区下志留统龙马溪组露头岩心照片，编号记为C1、C2、C3、C4，其中 C1的层理角度为 0°，C2为 30°，C3为 45°，C4为 90°（见图5）。

以C1、C2、C3、C4岩心为研究对象，对照片中的层理和基质骨架区域进行边缘提取、Hough直线检测[17]，建立4个数值模拟模型，编号分别记为D1、D2、D3、D4（见图6），其层理角度与 C1、C2、C3、C4一一对应。由于数字图像是由矩形排列的像素点组成，每个像素点是一个小正方形，这些小正方形均可作为有限差分计算中的四边形单元，故可将层理结构提取后的数字图像通过方形单元映射的方法可以很方便地转化成有限差分网格数据。首先，每个单元的 4个节点坐标通过图像实际尺寸与像素尺寸之间的比例关系，转换为相应矢量空间的物理坐标，整个图像就可转换为正方形有限差分网格，此法即为方形单元映射法。然后根据每个像素点所属灰度值，给每个单元赋予相应的参数，从而把数字图像表征的层理结构引入到数值模型中。最后，利用Matlab算法开展数值模拟计算，并将计算结果与超声波透射实验结果对比。从衰减系数结果图来看，数值模拟的衰减系数与层理角度呈正相关，这与超声波透射实验中岩心的衰减系数变化规律基本一致（见图7）。

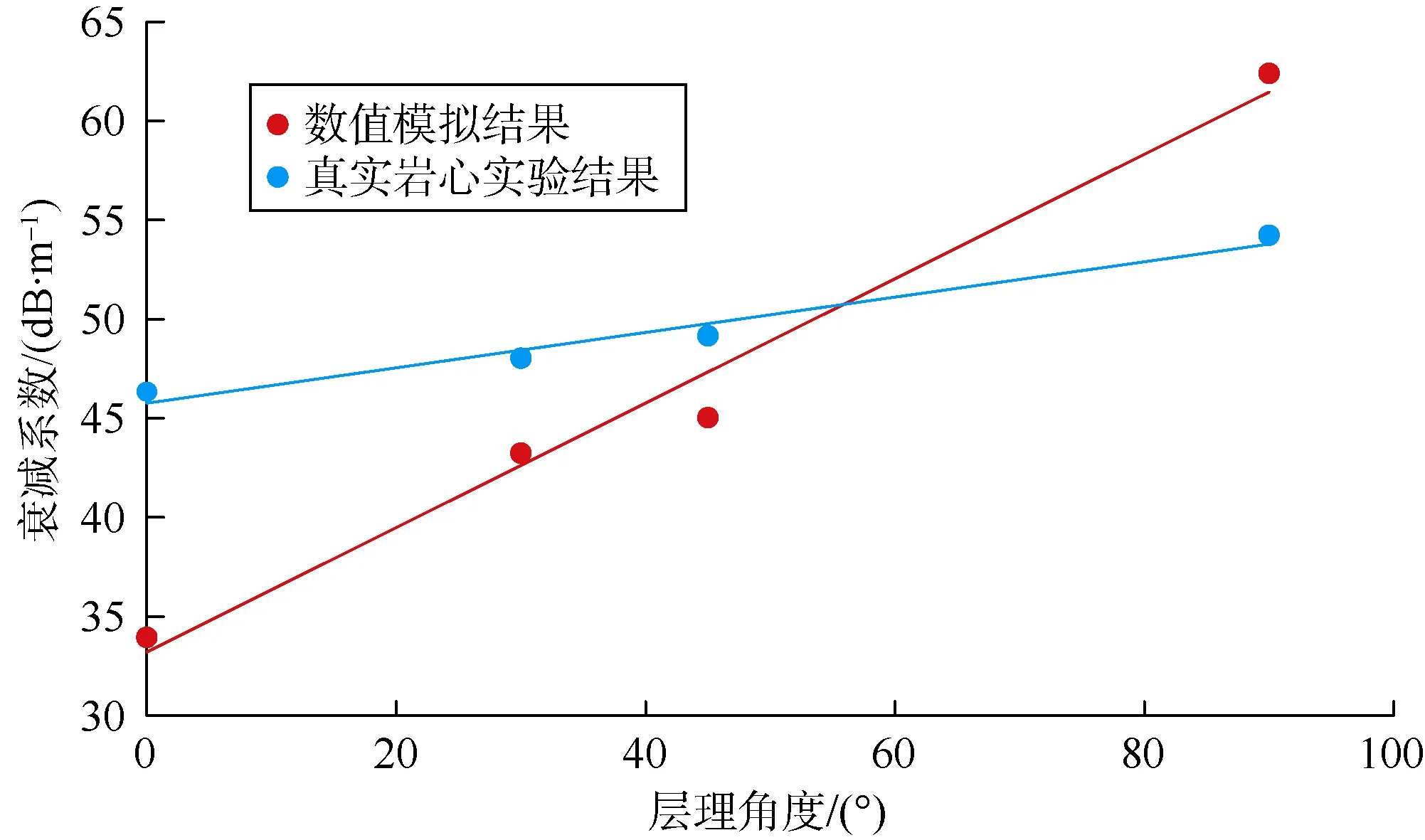
图7 实验结果与数值模拟结果图（样品数4个）

综上所述，针对超声波透射实验成本高，由于实验过程中岩心与探头接触不平整、人为数据读取等造成误差较大的现状[18]，本文提出的页岩超声波透射实验的数值模拟方法与实际超声波透射实验结果吻合度较高，因此，可依托此数值模拟计算手段，开展页岩层理结构声学特性研究。

2 页岩层理结构对超声波特征的影响

2.1 层理结构对超声波特性的影响

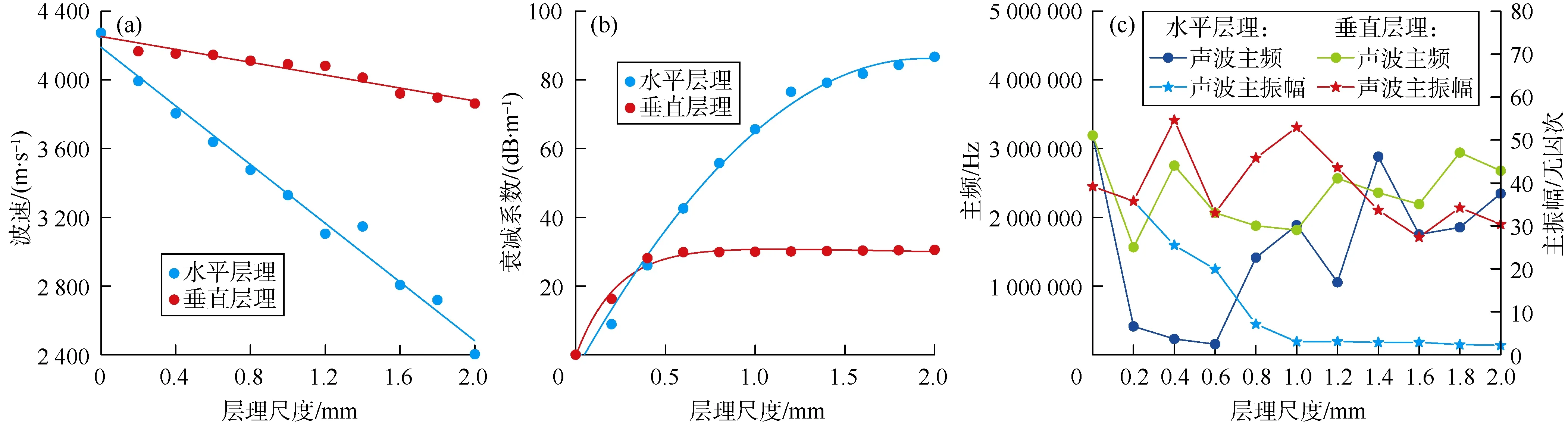
图8 不同层理厚度对超声波特性的影响（模型个数为22个）

页岩的显著特征是层理发育，表征层理结构的参数主要包括层理厚度、层理密度和层理角度。为了开展与超声波透射实验条件相吻合的数值模拟计算，本文将模型中的岩心柱塞高度设置为50 mm，直径为25 mm，页岩骨架中的纵波速度设为4 200 m/s，横波速度设为2 500 m/s；页岩层理中的纵波速度为1 900 m/s，横波波速为1 100 m/s；页岩骨架密度为2.6 g/cm3，层理密度为 2.3 条/cm2。提取实验室探头入射波作为初始波，保持超声波传播方向不变，将柱塞纵向剖面区域划分成长度为250 mm、宽为125 mm的网格，空间网格间距为0.2 mm，时间步长为20 ns。通过不断调整柱塞的层理模型参数来实现页岩结构的变化，完成对超声波透射实验的模拟，为探索层理结构对超声波特性的影响奠定基础。

2.1.1 层理厚度对超声波特性的影响

模型参数设置中，我们将平直且与层面平行的层理称为水平层理，定义平直且与层面垂直的层理为垂直层理。在层理角度和密度相同的情况下，将垂直层理厚度设为 0，0.2，0.4，0.6，0.8，1.0，1.2，1.4，1.6，1.8，2.0 mm，此组模型编号记为E1—E11。而另一组模型中水平层理厚度与垂直层理厚度设为相同，编号记为F1—F11。两组模型中超声波传播方向均为由其设置的岩心柱塞底端向顶端传播。本文从中选取了层理厚度结构特征比较明显的 E2、E10和 F2、F10模型，分析两组模型不同层理厚度对超声波特性的影响，并通过其波场快照图进一步开展层理厚度对超声波特性影响的微观分析。其中，E2的层理厚度为0.2 mm，E10的层理厚度为1.8 mm，F2层理厚度为0.2 mm，F10层理厚度为1.8 mm。由波速数值计算结果可知，随着层理厚度的增加，无论水平层理还是垂直层理，波速均呈线性递减，水平层理的递减幅度更大（见图8a）。衰减系数计算结果显示，随着层理厚度增加，无论水平层理还是垂直层理，衰减系数都呈增大趋势，其中水平层理的衰减系数以幂函数规律递增，而垂直层理以指数函数规律递增（见图8b）。超声波主频和主振幅计算结果显示，随着层理厚度的变化，水平层理中的超声波主频、垂直层理中的超声波主频与垂直层理中的超声波主振幅的变化无规律，而水平层理中的超声波主振幅随层理厚度的增大整体呈下降趋势（见图8c）。

前文预设模型中 E10垂直层理厚度比 E2的垂直层理厚度大，超声波由岩心底端到顶端传播。波场快照图显示，相同时刻下的超声波信号在E10中传播所能到达的距离比在E2中的更短（见图9a—图9b），所以导致超声波波速在E10中也较小（见图8a）。超声波在F2与F10中的水平层理传播也呈同样规律，即随层理厚度增大，在相同时刻下超声波信号在F10中传播距离也更短，说明超声波波速在F10中也较小。图9中使用不同的声场幅值来表征超声波透射能量大小，直观可见E10的颜色总体较E2更浅，说明随着垂直层理厚度增大，E10中透射超声波能量更小（见图9b），所以其衰减系数也较大（见图8b）。在模型F2和F10中的水平层理中也表现出与E2、E10同样的变化规律，即随层理厚度增大，透射超声波能量减小（见图9c—图9d），衰减系数增大（见图8b）。

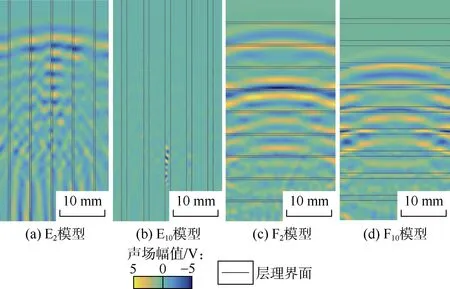
图9 层理厚度模型的波场快照

2.1.2 层理密度对超声波特性的影响

在层理角度和厚度恒定的条件下，通过调整层理数目来模拟层理密度变化，即岩心剖面单位面积上层理的数目。将垂直层理厚度设为0.4 mm，层理数目设为 0、1、2、4、5、6、10、12、15、18、20 条，对应的层理密度为 0、0.08×104、0.16×104、0.32×104、0.40×104、0.48×104、0.80×104、0.96×104、1.20×104、1.44×104和 1.60×104条/m2，此组模型编号记为 G1—G11。另一组模型编号记为 H1—H11，为水平层理，并将层理密度设置与上述一致。从中选取了能较好反映层理密度结构特征的 G3、G7和 H3、H7模型分析两组模型不同层理密度对超声波特性的影响，并通过其波场快照图，开展层理密度对超声波特性影响的微观分析。其中，G3的层理密度为0.16×104条/m2，G7的层理密度为 0.80×104条/m2，H3层理密度为 0.16×104条/m2，H7层理密度为 0.80×104条/m2。

由波速计算结果可知，随着层理密度的增加，无论水平层理还是垂直层理，波速均呈线性递减，垂直层理下降幅度相对较小（见图10a）。衰减系数数值计算结果显示，衰减系数随着层理密度的增加呈线性递增（见图10b）。超声波主频和主振幅数值计算结果显示，随着层理密度的增加，垂直层理中的超声波主频和主振幅变化无规律；但是在水平层理中，随着层理密度的增加，层理密度小于 0.3×104条/m2时，主频和主振幅呈下降趋势，层理密度大于 0.3×104条/m2后开始缓慢上升直到基本保持不变（见图10c）。

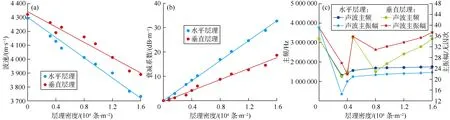
图10 不同层理密度对超声波特性的影响（模型个数为22个）

前文已对模型预设层理密度，由于模型中G7层理密度比G3层理密度大，H7层理密度比H3层理密度大，超声波由岩心底端到顶端传播，在G7中超声波通过层理与骨架的界面数目要比G3多，波场快照图显示，相同时间下的超声波信号在 G7中传播的距离比在 G3中的更短（见图11），所以超声波速度也较小（见图10a）。超声波在 H7与 H3中的水平层理传播也呈同样规律，即在相同时间下其超声波信号传播距离也更短，说明超声波波速也较小。在衰减特性方面，随着层理密度的增加，G7中层理条数比G3更多，非均质性更强。由于层理与骨架之间的模量不等，在骨架与层理之间产生一定的应变相位差，从而在界面处产生内摩擦，使机械能转为热能，极大消耗了能量[19]。图11中使用不同的声场幅值来表征超声波透射能量大小，直观可见G7颜色整体较G3更浅（见图11）；因此，G7中的超声波透射能量要明显低于G3，G7对应的衰减系数更大（见图10b）。H7与H3类似，也呈同样规律，即随着层理密度的增大，H7超声波透射能量更小，说明衰减系数更大。

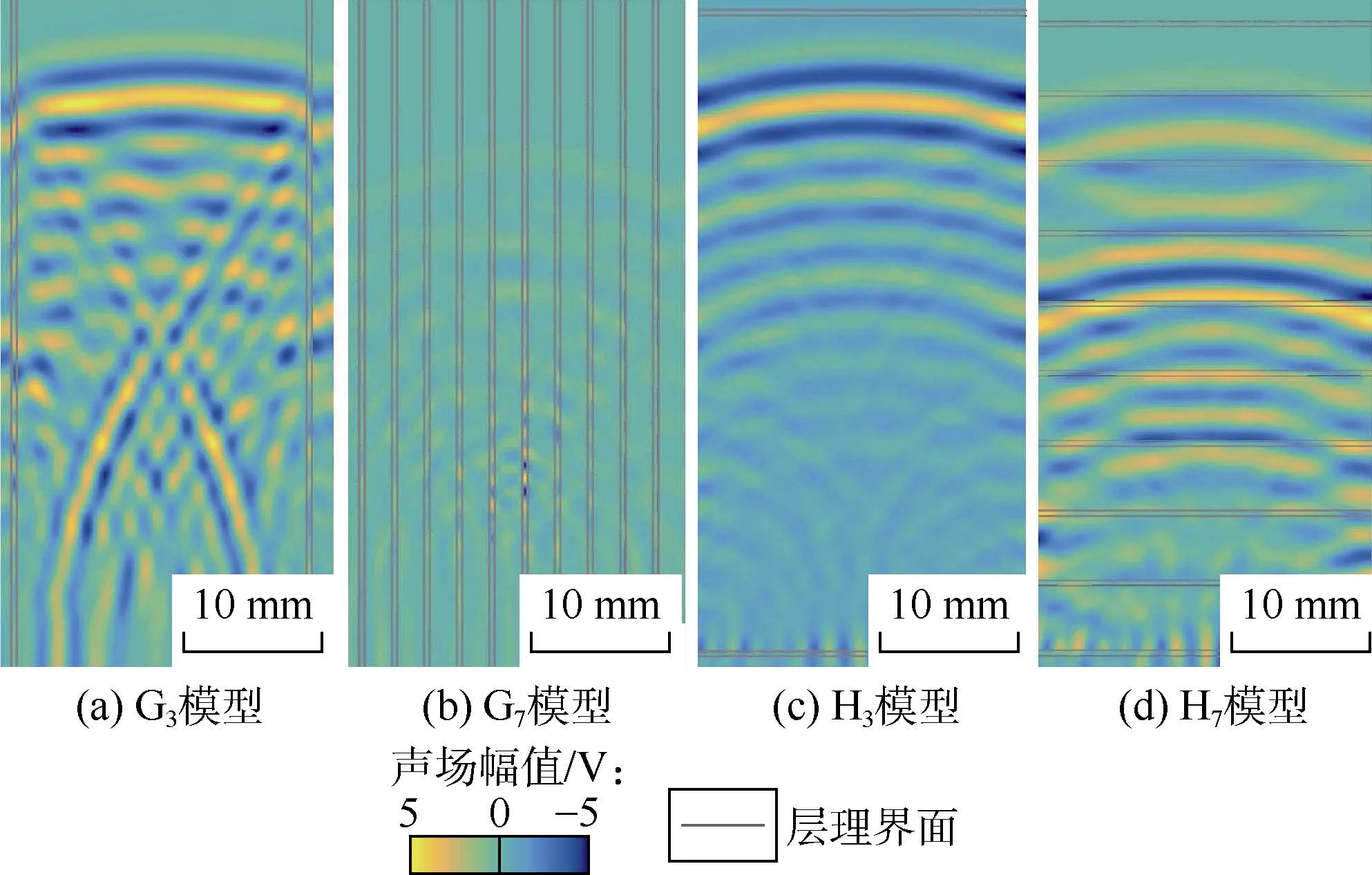
图11 层理密度模型的波场快照图

2.1.3 层理角度对超声波特性的影响

在层理厚度和密度恒定的条件下，将层理角度为0°、10°、20°、30°、40°、50°、60°、70°、80°、90°的模型编号记为 I1—I10。文中选取了层理角度特征比较明显的I3、I8，并通过其波场快照图进一步开展层理厚度对超声波特性影响的微观分析。其中，模型 I3的层理角度为30°，I8的层理角度为80°。

数值计算结果显示，随着层理角度的增加，波速呈幂函数递减规律（见图12a），而衰减系数呈线性递增规律（见图12b）。

由于模型预设I8的层理角度大于I3的层理角度，超声波由底端向顶端传播，在层理密度相同的前提下，I8的层理界面数目多于I3，波场快照图显示，在相同时刻下I8中超声波信号传播所能到达的距离比在I3中的更短（见图13a—图13b），对应的波速也就较小（见图12a）。在衰减特性方面，由于I8中的骨架与层理面之间的界面个数多于 I3，导致阻碍超声波传播的路径也多于I3，图13中使用不同的声场幅值来表征超声波透射能量大小，直观可见I8的颜色总体较 I3更浅，说明透射超声波能量更小，所以衰减系数也较大，对应的衰减系数更大（见图12b）。

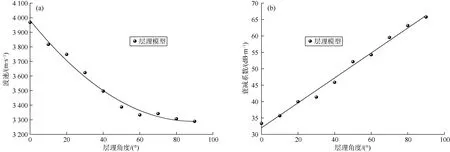
图12 不同层理角度对超声波特性的影响图（模型个数为11）

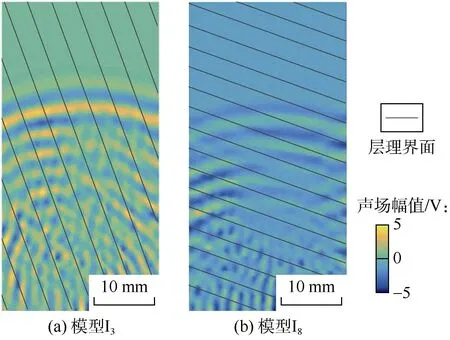
图13 层理角度模型的波场快照图

2.2 超声波特性统计分析

在页岩数值模拟计算结果的基础上，利用灰色系统关联法[20]定量分析声学参数对层理结构的敏感性。首先，将超声波速度、衰减系数等声学参数作为参考序列，将层理角度、密度和厚度变化等层理结构变化参数分别作为比较序列：

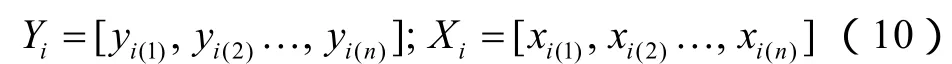
对序列中的数据进行均值无量纲化处理，即：

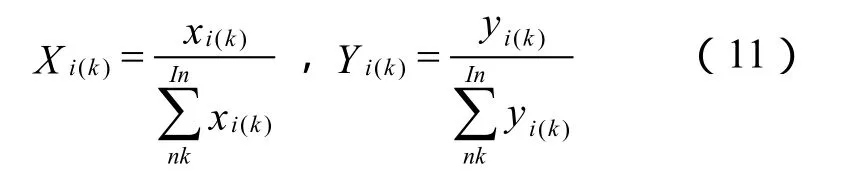
求取序列的关联系数：

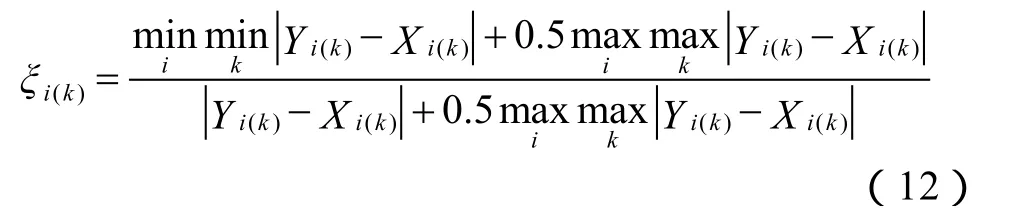
获取整个数列的关联度：

声学参数中不仅速度对层理角度和层理密度的变化较为敏感（关联度值均为0.80以上），衰减系数对层理厚度的变化也较敏感（关联度值可达0.89），而主振幅、主频与层理结构相关联度则相对较小（关联度均在 0.60以下）（见表1）。因此，在进一步利用声学参数表征页岩层理结构的过程中，除了选用常规敏感因子速度之外，还需配合衰减系数来综合描述。

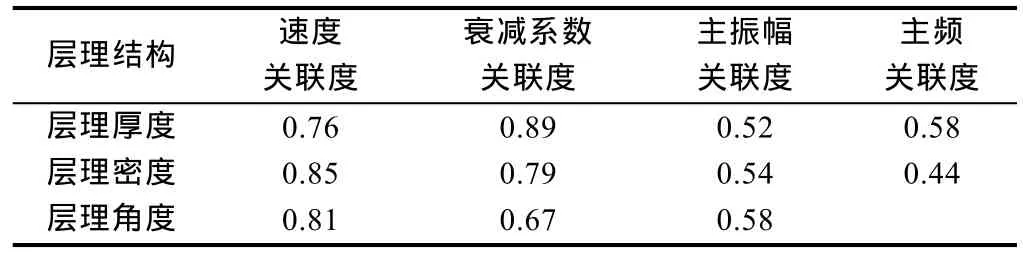
表1 层理结构参数和各个影响因子的关联度

3 页岩动态力学参数模型研究

3.1 页岩动态力学参数模型建立

利用岩石波速建立动态力学参数模型是现场油气井开发中最常用的方法。其中各向同性模型和横向各向同性模型表达式如下所示：

各向同性岩石力学参数预测模型：

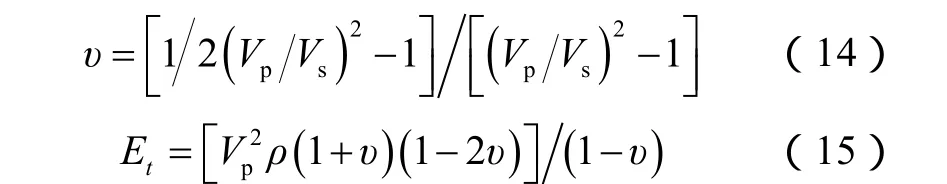
横向各向同性岩石力学参数预测模型[21]：

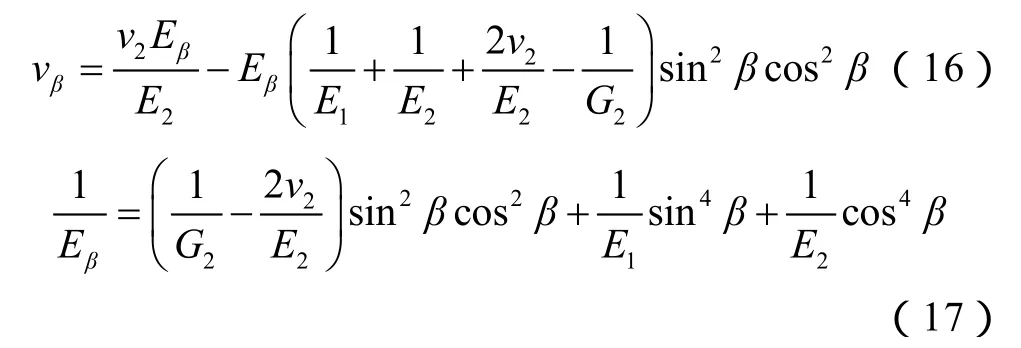
通过数值模拟研究发现，仅通过波速建立页岩的动态力学参数模型是不可行的，还需配合对岩石各向异性特征敏感的衰减系数，方能达到更好效果。利用实验测得的渝东南彭水地区井下龙马溪组页岩的波速和衰减系数，基于麦夸特与全局优化算法[22]在考虑量纲的基础上，建立了该地区页岩的动态力学参数模型：

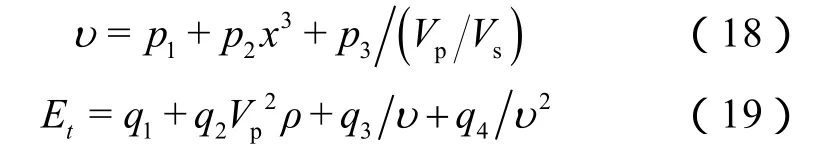
3.2 模型室内对比验证

采用渝东南ZY1井和YY1井的井下岩心开展基础物性实验获取岩心密度，通过岩石力学实验获取弹性模量和泊松比，利用超声波透射实验获取纵、横波速度（见表2）。在此基础上，对本文模型进行验证。将表2中实验结果代入由公式（14）、（15）所建立的各向同性模型，以及由公式（16）、（17）所建立的横向各向同性模型，开展模型的对比分析。

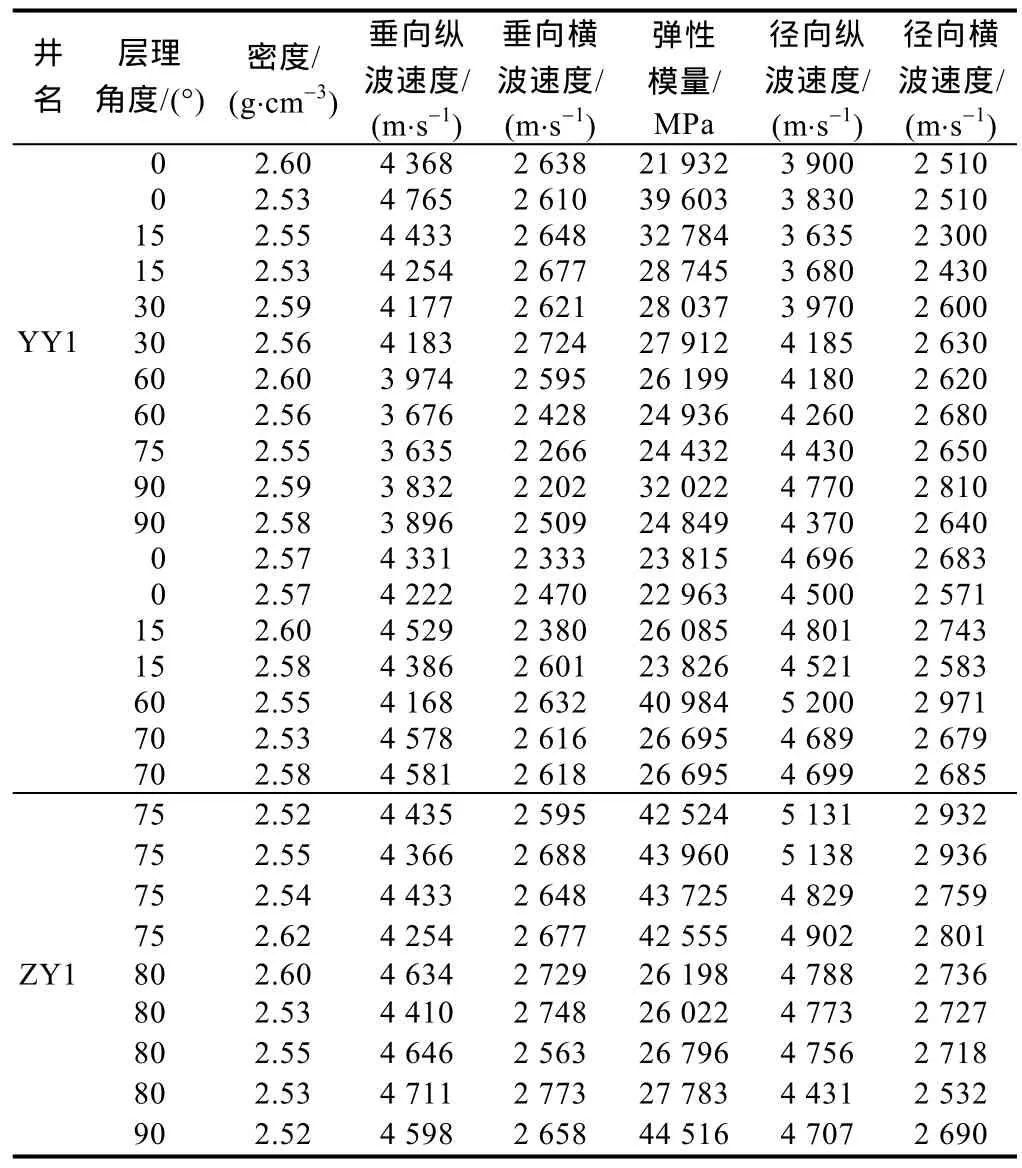
表2 井下岩心实验结果

验证结果表明：利用本文模型计算得到的动、静态力学参数相关性整体较好，其中在ZY1井中静态泊松比与动态泊松比相关系数可达 0.83，静态弹性模量与动态弹性模量相关系数可达0.84。在YY1井中静态泊松比与动态泊松比相关系数可达 0.82，静态弹性模量与动态弹性模量相关系数可达0.81（见图14）。本文的新模型模拟效果优于通常使用的各向同性模型和横向各向同性模型，其中各向同性模型是指不同方向上物理性质相同的介质，为均质模型；横向各向同性模型是指垂直于轴线的任何方向上弹性相同，为非均质模型。究其原因，是因为各向同性模型只针对各向同性的岩石，未考虑页岩的层理发育，而横向各向同性模型将页岩等效为横向各向同性体处理，模型结构过于理想化，影响准确性，而本文模型是基于表征页岩层理结构最为敏感的波速和衰减参数，利用通用全局优化算法求得，模型可较好地反映页岩层理结构的影响，而且本文计算得到的岩石动态模量一般大于静态模量，动态泊松比与静态泊松比基本为1︰1关系，与Kuhlman等得到的关系基本一致[23]。

3.3 模型现场验证

收集渝东南地区ZY2井的测井资料开展岩石力学动态参数剖面反演，获取静态力学参数剖面结果。从图15中看出，在反演深度范围内，动态弹性模量数值普遍大于静态弹性模量数值，动态泊松比与静态泊松比数值很接近，基本为 1︰1，这与前文所述模型计算结果保持一致。同时，取ZY2井龙马溪组不同深度的10块岩心开展岩石力学实验，将实验结果与现场测井资料的反演数据进行验证。

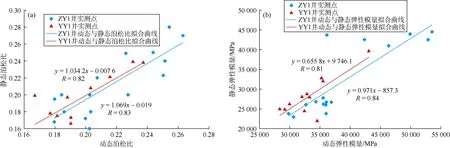
图14 动态力学参数模型的对比验证图（R—相关系数）

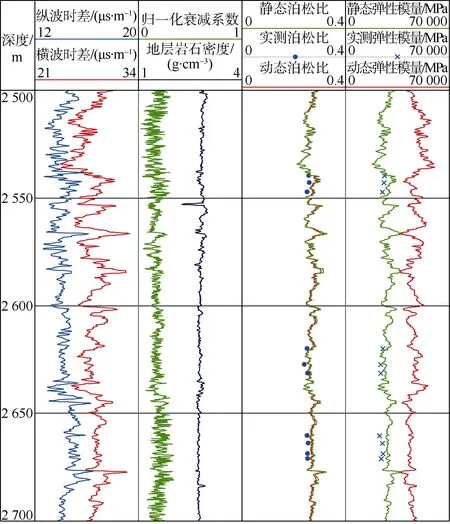
图15 ZY2井下志留统龙马溪组岩石力学参数预测结果图

由表3可见，10个不同深度反演得到的力学参数值与对应井下岩心的实验测试值基本一致。通过计算两者的相对误差可知，泊松比的相对误差小于 10%，平均相对误差为 6.94%；弹性模量最大相对误差为21.25%，平均误差为15.30%。可见，利用测井资料反演的力学剖面能准确地反映地层力学参数真实情况，本文建立的动态力学参数模型对层理发育的页岩地层有较好的适应性。

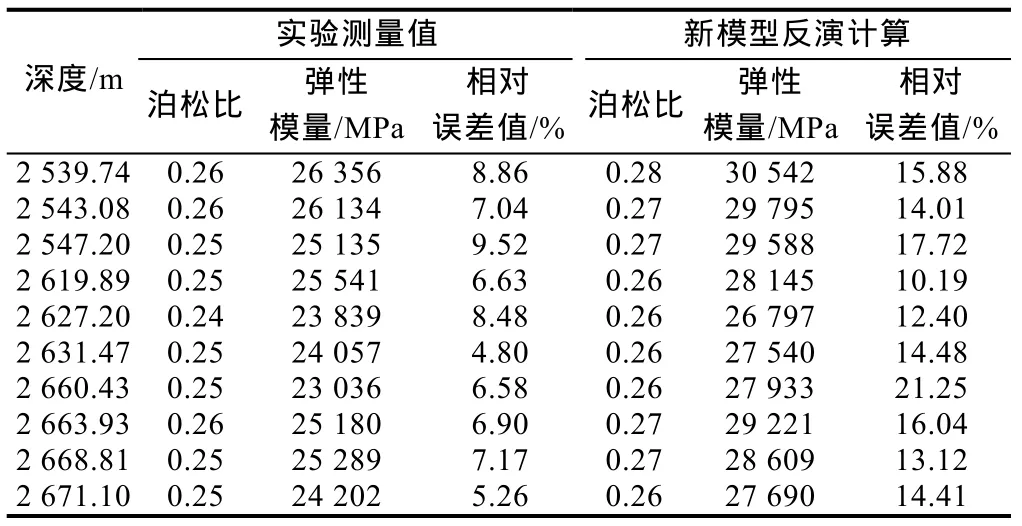
表3 现场静态力学参数验证误差分析表

4 结论

基于波动理论，利用交错网格有限差分法，获取了一种页岩超声波透射实验的数值模拟方法。该方法模拟波形与实验波形相关系数大于 80%，表明数值模拟方法可有效模拟超声波透射实验。

超声波参数中，声波速度是用来表征页岩层理结构的常规敏感因子，但还需要利用衰减系数的归一化结果来综合描述页岩层理，可使结果更加准确。

利用页岩超声波透射实验的波速和衰减系数建立了渝东南下志留统龙马溪组超声波预测页岩力学参数模型，此模型计算得到的动、静力学参数相关性优于传统模型，利用模型和测井资料反演而获取的岩石力学剖面预测值与实验值吻合较好。

符号注释：

A，B——速度u和ν的离散值，无因次；Cn(k)——待定差分系数，无因次；D——应力τxx的离散值，无因次；D0——标准差，无因次；E——应力τxz的离散值，无因次；E0——期望值，无因次；Et——弹性模量，MPa；Eβ——任意角度β方向的弹性模量，MPa；E1、E2——表示平行和垂直各向同性面的弹性模量，MPa；F——应力τzz的离散值，无因次；G2——各向同性面内的剪切模量，MPa；i，j，k——空间和时间网格点，无因次；p1、p2、p3，q1、 q2、q3——模型系数，无因次；ri——Xi(k)与Yi(k)的关联度，无因次；R——相关系数，无因次；R1——声波震动位移，m；Δt——时间网格间距，无因次；u——x方向的速度分量，m/s；ν——z方向的速度分量，m/s；U——x方向的位移函数，无因次；V——z方向的位移函数，无因次；Vp、Vs——岩心纵、横波速度，m/s；ν1、ν2——分别表示平行和垂直各向同性面的泊松比，无因次；Xi——表示比较序列，无因次；Yi——表示参考序列，无因次；Δx，Δz——空间网格间距，无因次；β——层理面与岩样端面间的夹角，°；λ，μ——拉梅常数，无因次；ρj——岩心密度，g/cm3；ρij——表示质点在x、z坐标轴中密度的离散值，g/cm3；τxx、τxz、τzz——应力分量，MPa；χ——归一化衰减系数，无因次。