利用纳米压痕实验研究层理性页岩岩石力学性质——以渝东南酉阳地区下志留统龙马溪组为例

时贤，蒋恕 ，卢双舫，何治亮，李东杰，汪志璇，肖佃师

（1. 中国石油大学（华东）石油工程学院，山东青岛 266580；2. Energy & Geoscience Institute, University of Utah,Salt Lake City, UT 84102, USA；3. 中国石油大学（华东）地球科学与技术学院，山东青岛 266580；4. 页岩油气富集机理与有效开发国家重点实验室，北京 100083）

0 引言

受益于水力压裂和水平井技术的快速进步，页岩气的勘探与开发取得了巨大商业化成功，改变了全球能源格局[1-2]。岩石的弹性模量、硬度、断裂韧性等力学参数对研究页岩压裂改造时的复杂缝网形成和延伸规律，以及开展甜点评价和进行钻井工程设计都具有重要意义。传统单轴或者三轴岩石力学实验等宏观力学参数测试方法对试样尺寸和完整性都有较高要求，但因为岩石本身物理化学性质的不稳定性，以及弱层理面或者天然裂缝的发育，使得取心质量难以保证，加大了力学实验测试难度。传统力学实验测试方法由于测试价格昂贵、实验周期较长，通常只能在勘探井重点层位或者局部区域进行取心力学测试，造成测试数据结果离散性较大，易产生争议性，并且很难为压裂设计提供力学参数的连续解释剖面，工程价值有限。除此之外，传统力学压缩测试属于破坏式实验，实验岩心在加载破坏后无法再继续进行其他力学测试，实验可重复性较差，也降低了岩心的利用价值[3-4]。因此，寻求高效、简单且可靠的力学参数测试方法和手段一直是油气工业界的热点关注问题。

纳米力学测试方法是近年来表面工程力学性质测试中快速发展的一项重要技术，具有无损、分辨率高、操作方法简便等优势，可以对材料的硬度、弹性模量、塑性应变以及疲劳强度等关键力学特性进行分析，已经被广泛应用于精密和超精密材料的力学参数测试工作。近年来，将纳米力学测试方法应用到岩石力学测试也逐渐受到了学者普遍重视并取得了一些阶段性成果[5]。纳米力学测试方法极大地降低了对岩石试样质量和尺寸的要求，尤其是可以对产层或者重点层位的钻井岩屑进行连续力学测试，为后续和测井曲线关联与校正开辟了新的途径。页岩微观内部结构、矿物颗粒组成、干酪根分布等特点与页岩气的成藏和宏观力学变形紧密相连，纳米力学测试可以和原子力显微镜、数字岩心、3D打印等数字成像技术有效结合，为开展页岩气成藏运移、孔喉分布精细表征、微观结构力学性质等“一体化”评价提供更多潜在应用价值。陈平等[6-7]采用微米级力学测试方法对页岩的硬度和弹性模量进行分析，提出微米尺度下岩石力学参数的计算模型，并发现纳米压痕与微米压痕实验结果具有较好的相关性。Bobko等[8]发现纳米尺度下的页岩矿物颗粒在刚度上属于横观各向同性，在强度上则属于各向同性。Shukla和 Kumar等[9-10]利用纳米压痕技术结合背散射电子衍射（BSE）等测试手段标定压痕位置，围绕纳米尺度下的干酪根力学性质进行测试与分析，发现干酪根的弹性模量为5～9 GPa，较高的干酪根含量会整体降低岩石弹性模量。Liu等[11]利用场发射扫描电镜（FE-SEM）和数字图像处理方法，建立纳米尺度下Bakken页岩孔隙结构、孔径分布和岩石力学性质之间的关联性。目前研究成果大多集中在对纳米尺度下页岩弹性模量、硬度、断裂韧性等参数的测试，并利用均值统计法对力学参数进行计算，但力学参数样本数据分布特征以及纳米尺度向宏观尺度的力学参数升级模型则较少涉及，同时考虑页岩层理条件的相关测试数据并不丰富，从而限制了纳米压痕技术在页岩力学性质表征方面取得更为广泛和合理的应用[12-14]。

本文以渝东南酉阳地区下志留统龙马溪组页岩为研究对象，利用氩离子抛光设备制备平行层理和垂直层理的试样，采用网格压痕测试方法开展纳米压痕实验，得到岩石弹性模量、硬度、断裂韧性等力学参数，结合能量色散 X射线荧光光谱（EDS）数据实现对标定矿物的力学参数测试分析。利用Weibull模型分析纳米尺度下各力学数据分布特点和数据离散产生的相关原因，提出采用Mori-Tanaka模型作为从纳米尺度向厘米尺度升级的力学参数模型，并利用单轴岩石力学实验结果和压痕实验结果进行对比验证。实验成果将有助于研究龙马溪组纳米尺度下的层理性页岩力学性能参数、实现纳米尺度力学参数向宏观尺度力学参数升级。

1 纳米压痕原理与实验

1.1 纳米压痕基本原理

在进行纳米压痕实验时，压头逐渐压入试样后，压头附近的材料首先产生弹性变形，随着载荷的增加，试样开始产生塑性变形，样品中出现一个与压头形状匹配的压痕。当压头卸载时，弹性变形得到恢复，而塑性变形则形成压痕裂缝。通过实验数据绘制纳米压痕载荷-位移变化曲线，并利用该曲线计算岩石的弹性模量和硬度（见图1）。

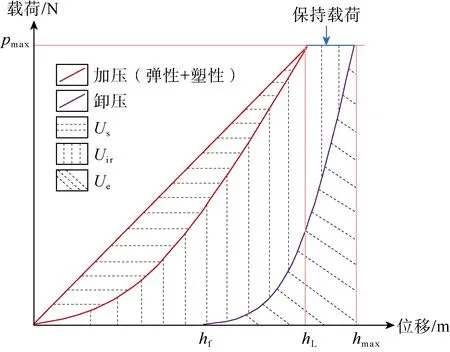
图1 纳米压痕载荷-位移变化曲线示意图（据文献[12]修改）

硬度的计算公式为[15]：

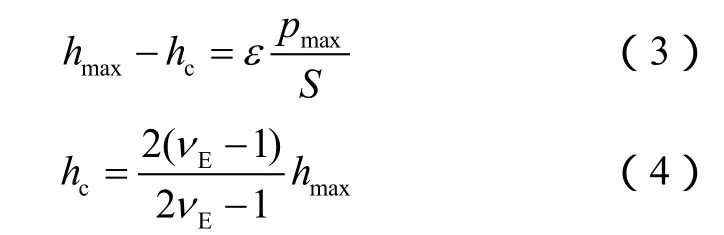
其中，hc与hmax有如下关系：得到接触投影面积和接触深度后，可通过下式计算出折算弹性模量：

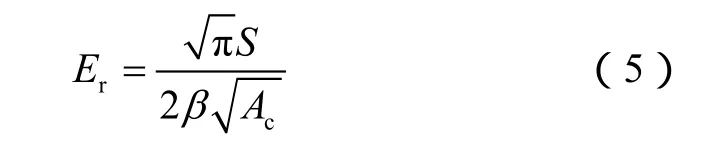
折算弹性模量可以用来体现压头和试样的复合弹性形变，并可以转化为试样的真实弹性模量，计算表达式为：

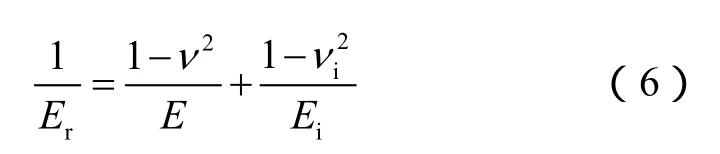
断裂韧性是表征外力作用下材料抵抗裂纹扩展的能力[16]。纳米压痕试验可以采用压痕形貌法和能量分析法来测定断裂韧性。本文选择能量分析方法进行岩石断裂韧性的计算，关于能量分析方法和压痕形貌法在计算岩石断裂韧性上的差异性将在另外文献中阐述。根据 Yang等[17]的理论，裂缝断裂能量可以由纯塑性阶段耗失的能量和不可逆能量（总裂缝能量与弹性能量的差值）来确定：

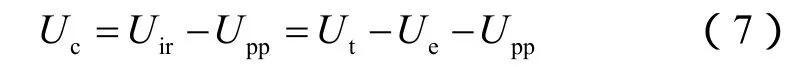
式中，Upp与Ut存在以下关系：

其中，Ut可以利用下式计算得到：

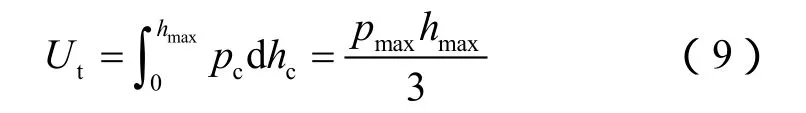
在进行断裂韧性计算之前，需要先利用下式计算出裂缝产生的临界能量释放率：

对于波氏（Berkovich）压头而言，这个区域可以利用下式直接计算：

由此得到岩石断裂韧性的计算表达式：

1.2 纳米压痕实验设备与材料

实验选取渝东南酉阳地区下志留统龙马溪组埋深约2 010 m的页岩岩心4块。首先将岩心加工为直径25 cm、长度55～60 mm的柱状体，再切割成直径25 mm、长度50 mm的标准岩石力学测试岩心和直径25 mm、长度10 mm的压痕岩心，其中垂直层理标准试样标记为VA和VB、平行层理标准试样标记为HA和HB、垂直层理纳米压痕试样标记为V1和V2、平行层理纳米压痕试样标记为H1和H2。

在纳米压痕实验中，局部微孔隙或不同物相界面处的粗糙度突变都会影响测试结果的精确性，为此采用碳化硅砂纸对试样表面进行多次机械抛光，再采用宽束氩离子设备进行二次抛光，以获得表面平滑的样品，同时借助Zeta-20三维形貌仪随机扫描岩石表面以确保满足粗糙度要求。之后，需要对样品进行超声清洗，再用丙酮对纳米压痕实验的样品进行处理，以去除锈斑等污垢[18-19]。采用RoqSCAN设备进行岩石矿物组分分析，可以一次得到SEM、BSE、EDS等图像来标定不同矿物位置以方便确认压痕测试数据。在纳米压痕实验后，同时对压痕位置进行二次SEM扫描，以掌握压痕形态面貌。

纳米压痕实验中所用的力学设备为美国安捷伦Nano Indenter®G200，载荷分辨率为50 nN，标准测试最大载荷500 mN，z方向位移分辨率小于0.01 nm，最大压入深度大于 500 μm，x、y方向位移分辨率为 1 μm，行程范围为100 mm×100 mm。采用顶端曲率半径小于20 nm的波氏压头。

1.3 纳米压痕实验步骤

实验分为3个步骤进行。

①纳米压头以 30 nm/s的载荷下降速率向试样表面逐渐靠近，当测试系统显示载荷突然增大时表示压头已经接触到试样表面，此时系统按设定方式开始加载并自动记录载荷以及对应的压入深度。对每块试样进行测试时，最大载荷设定为500 mN并保持15 s。

②首先利用已知纳米尺度下的材料力学参数对测试参数进行标定。然后在每个页岩试样表面进行包含32个压痕的测试点阵（4个样品合计128组）弹性模量、硬度和断裂韧性实验数据测量，计算每个样品的力学参数均值。利用EDS对试样表面进行分析和特定矿物定位，计算不同矿物的纳米压痕测试力学参数。

③采用全数字型液压伺服刚性材料实验机对垂直和平行层理样品进行单轴压缩测试，获取宏观力学参数，并将结果与尺度升级结果和纳米压痕均值计算结果进行对比分析。

2 纳米压痕实验结果

2.1 页岩矿物组成和微观结构

龙马溪组页岩试样BSE扫描结果显示，矿物颗粒胶结较好，大尺寸孔隙几乎不发育，只存在少量微孔隙（见图2a）。利用 EDS处理得到矿物组成的质量分数和面积分数以及矿物分析统计（见表1）。统计数据结果显示，本文试样的矿物成分主要由石英类矿物（石英、纳长石、钾长石）、碳酸盐类矿物（方解石、白云石）、黏土矿物（伊利石、高岭石、绿泥石）组成，另外还含有少量蒙皂石、白云母、黄铁矿以及非晶物质等难以区分的矿物。

图2 页岩矿物垂直层理组分分析测试结果

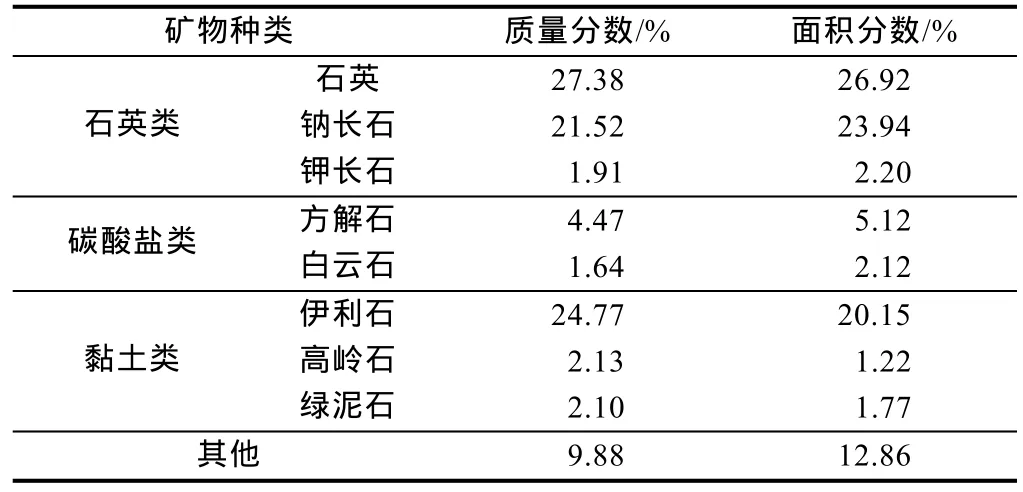
表1 页岩矿物垂直层理组分分析结果表

点阵压痕和单个纳米压痕的SEM结果显示（见图3a），压痕形貌反映出试样本身具有一定数量的微观缺陷（孔隙和微裂缝），在纳米压痕过程中，载荷随着压入位移的增加会在试样表面形成微裂缝，微裂缝向四周的扩展延伸会受到试样本身微观缺陷的影响。一般情况下，裂缝都更易沿孔隙或者已存在微裂缝的边沿扩展。由于页岩本身的非均质性，特别是如果压入位置恰好为较硬的碳酸盐类矿物，而压入位置之下为黏土类等较软的矿物，则有可能出现“基底”效应，即出现黏土堆积现象，影响纳米压痕力学解释结果（见图3b）。

2.2 载荷-位移曲线

载荷-位移曲线是分析纳米压痕变形行为和力学参数的基础。纳米压痕实验获取的部分载荷-位移曲线并不光滑，在加载阶段存在突进现象（见图4a）。产生加载突进的主要原因是当载荷增加达到屈服强度后，岩石出现了微裂缝，应力随着裂纹尖端开始向里扩展，在加载过程中由裂缝接触位置自外向内不断重复这个过程。另外也有极大可能是由于页岩本身的非均质性造成压痕生长过程中裂缝经过不同强度矿物分布区域，特别是微裂纹、微孔洞等内部缺陷或者干酪根等力学强度较软的物质的存在导致界面效应的产生，致使载荷恒定加载过程中出现跳跃。纳米压痕实验过程中的页岩加卸载曲线由弹性变形、弹塑性变形和塑性变形3个阶段组成，不同样品因为力学性质的差异导致各阶段持续的时间并不相同。图4a显示在位移为1 000 nm时开始由弹性阶段进入弹塑性阶段，而图4b则显示在2 000 nm以后才由弹性阶段进入弹塑性阶段。加载时，载荷-位移曲线的曲率在弹性和弹塑性阶段会迅速增大，反映在纳米压头与页岩表面接触时首先产生快速的弹性变形，在达到岩石本身屈服强度后，则发生弹塑性变形并开始出现纳米压痕裂纹，压入载荷超过岩石本身强度之后则开始出现塑性破坏并形成永久裂缝。

图3 纳米压痕后的载荷点阵SEM图片（a）及单个SEM图片（b）

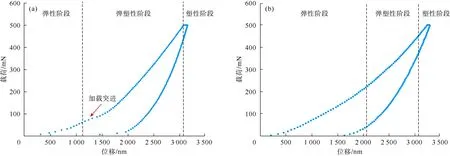
图4 具有加载突进现象的（a）及正常的（b）纳米压痕载荷-位移曲线

2.3 纳米尺度下力学参数测试结果

通过分析载荷-位移曲线，结合（1）式和（6）式可以计算出岩石的硬度和弹性模量等力学参数，并通过（12）式计算岩石的断裂韧性。由于纳米压痕实验数据量较大，通常采用均值统计法或解卷积法对力学参数进行处理，解卷积法需要明确区分岩石相态组成且可能存在多解性，因此本文采用均值统计法进行数据分析。128组力学参数统计数据显示（见表2），平行层理试样的平均弹性模量为45.21 GPa（标准差为5.59 GPa）、平均硬度为2.43 GPa（标准差为0.56 GPa）、平均断裂韧性为 2.68 MPa·m1/2（标准差为 0.33 MPa·m1/2）；垂直层理试样的平均弹性模量为43.60 GPa（标准差为4.03 GPa）、平均硬度为 2.85 GPa（标准差为 0.78 GPa）、平均断裂韧性为 2.37 MPa·m1/2（标准差为 0.66 MPa·m1/2）。整体上平行层理面的岩石弹性模量和断裂韧性略高于垂直层理面。在纳米尺度下，由于测试压痕点位于不同的矿物表面，会导致力学参数具有一定的波动性。因此，为了获取更为可靠的力学参数值，需要进行更多的压痕测试，以消除岩石本身非均质性所带来的不确定性。

在页岩表面进行纳米压痕测试后，借助EDS矿物标定结果，可以得到属于不同矿物的力学参数，从而为后续力学参数等效模型的建立以及实现纳米尺度向宏观尺度升级提供参数。本文实验得到的纳米压痕力学测试结果与其他学者的实验结果[9-10]相比具有较好的一致性（见表3），由于本文实验矿物中绿泥石、黄铁矿等矿物含量较少，所以没有得到相关的压痕数据。除了对指定矿物开展纳米压痕测试外，还对石英和黏土类矿物交界处进行了纳米压痕分析，分析结果显示白云石和石英的弹性模量最高，分别为 115 GPa和 99 GPa；而黏土类矿物的弹性模量最低，其中高岭石和伊利石的弹性模量分别为55 GPa和62 GPa；石英/黏土基质交界混合矿物的弹性模量则介于两者之间，约为59 GPa。

表2 纳米压痕力学参数统计表

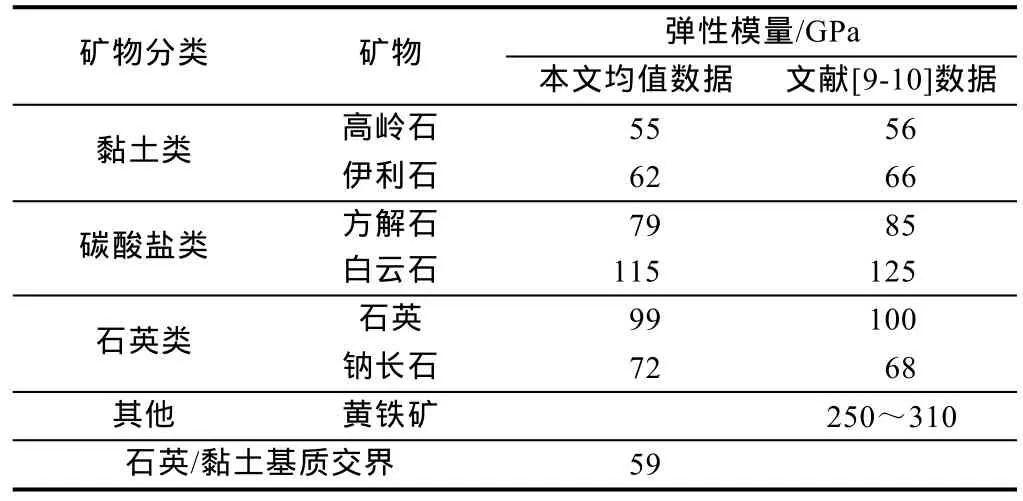
表3 特定矿物纳米压痕力学参数统计表

3 讨论与分析

3.1 纳米尺度下岩石力学性质之间的关联性

通过线性回归分析发现，平行层理和垂直层理条件下纳米压痕实验得到的弹性模量和硬度之间、弹性模量和断裂韧性之间均具有正相关关系，相关系数分别为 0.57和0.58（见图5）、0.54和0.51（见图6）。但是，平行层理条件和垂直层理条件下纳米压痕测得的硬度和断裂韧性之间的线性回归关系较差，相关系数分别为0.31和0.36（见图7），主要原因在于计算硬度时只利用了加载时的接触投影和载荷等信息，而计算断裂韧性时则利用整个加卸载曲线下的阴影面积，引入计算参数的差异造成了最终计算结果回归关系不明显。因此，除了需要提高压痕测试数量以降低数据离散性以外，还需要加强对接触深度、接触刚度和残余深度等核心输入参数的精确计算。

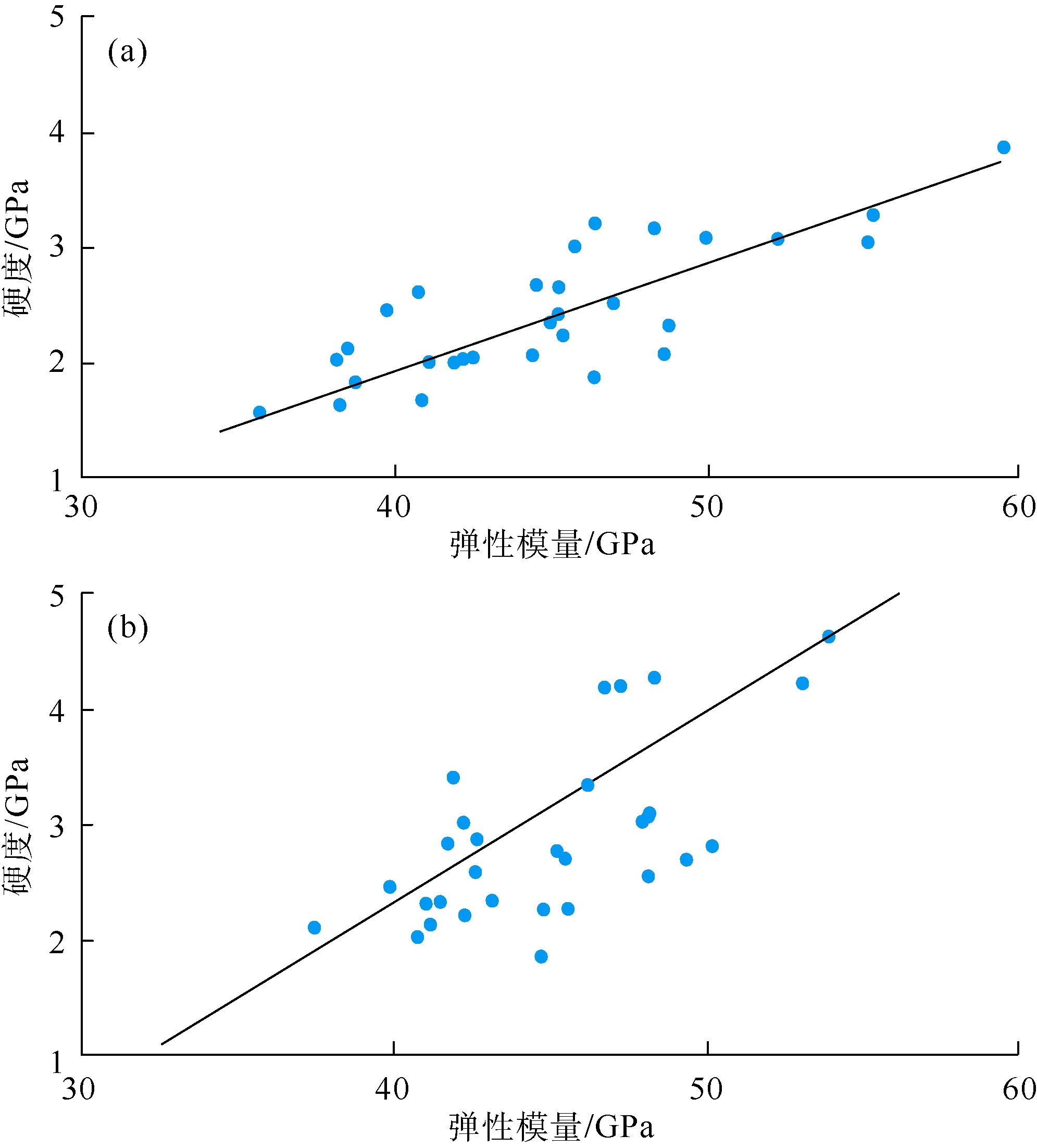
图5 平行层理（a）和垂直层理（b）条件下弹性模量与硬度关系图

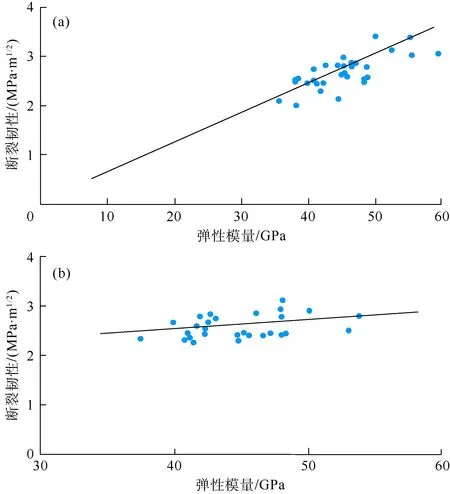
图6 平行层理（a）和垂直层理（b）条件下弹性模量与断裂韧性关系图

3.2 纳米尺度下岩石力学性质分布

纳米压痕实验分析结果显示岩石的弹性模量、硬度、断裂韧性均存在一定的波动性，如在平行层理条件下，弹性模量最大值为59.47 GPa、最小值为35.61 GPa，最大值是最小值的1.67倍，原因是实验样品具有非均质性，因此需要对测试结果进行统计分析，以掌握纳米压痕实验结果的不确定性特征。宏观和细观岩石力学实验结果表明，Weibull模型可有效表征岩石的非均质性与外部环境条件作用下岩石力学响应特征，且分布形状参数的数值较易测量[20-21]。Weibull模型表达式为：

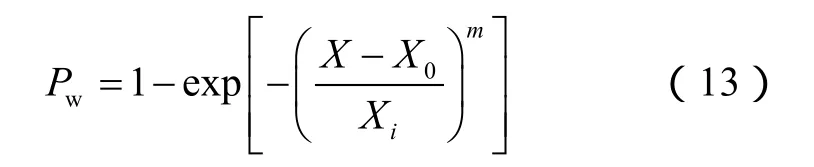
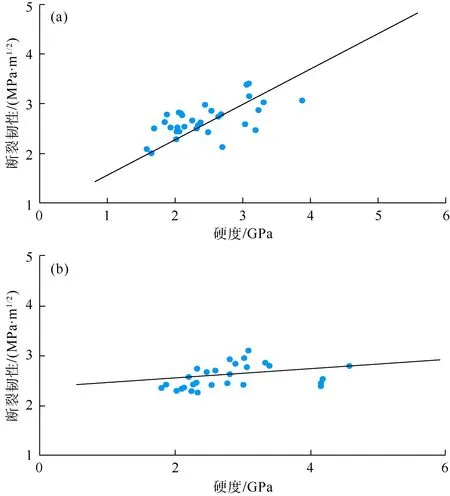
图7 平行层理（a）和垂直层理（b）条件下硬度与断裂韧性关系图

式中，Pw为力学参数不高于X的概率，Xi为特征参数，X0一般设为 0，代表最小变量参数值。式中m称为Weibull模数，反映整个力学参数的离散性，m值越高表明离散性越小。

将纳米压痕实验得到的统计结果按数值大小进行顺序排列，得到每个实验结果不高于X的概率，采用最小二乘法得到m值（见表4）。各力学参数的Weibull回归曲线结果显示（见图8—图10），3个力学参数的m值均较小，说明纳米压痕测试中实验数值离散性较高，其中硬度的m值最小、离散性最高。造成数据离散的本质原因是：①岩石表面和内部矿物颗粒尺寸、形状及排列的差异，以及压痕位置不同造成纳米压痕实验结果存在差异；②在压痕形成裂缝扩展延伸时，尺寸较大或者强度较高的颗粒改变了局部应力场分布，导致压痕裂缝发生偏转和阻碍，造成实验数据出现跳跃；③硬度计算中仅依赖于压痕投影面积，而具有不同强度性质的颗粒会造成压痕在局部区域出现“基底”效应，影响压痕投影面积预测结果的准确性，进而影响硬度计算精度。同时还发现，垂直层理测试条件下的m值均小于平行层理，说明垂直层理试样较平行层理试样具有更高的非均质性。

表4 纳米压痕力学参数的m值统计分析结果

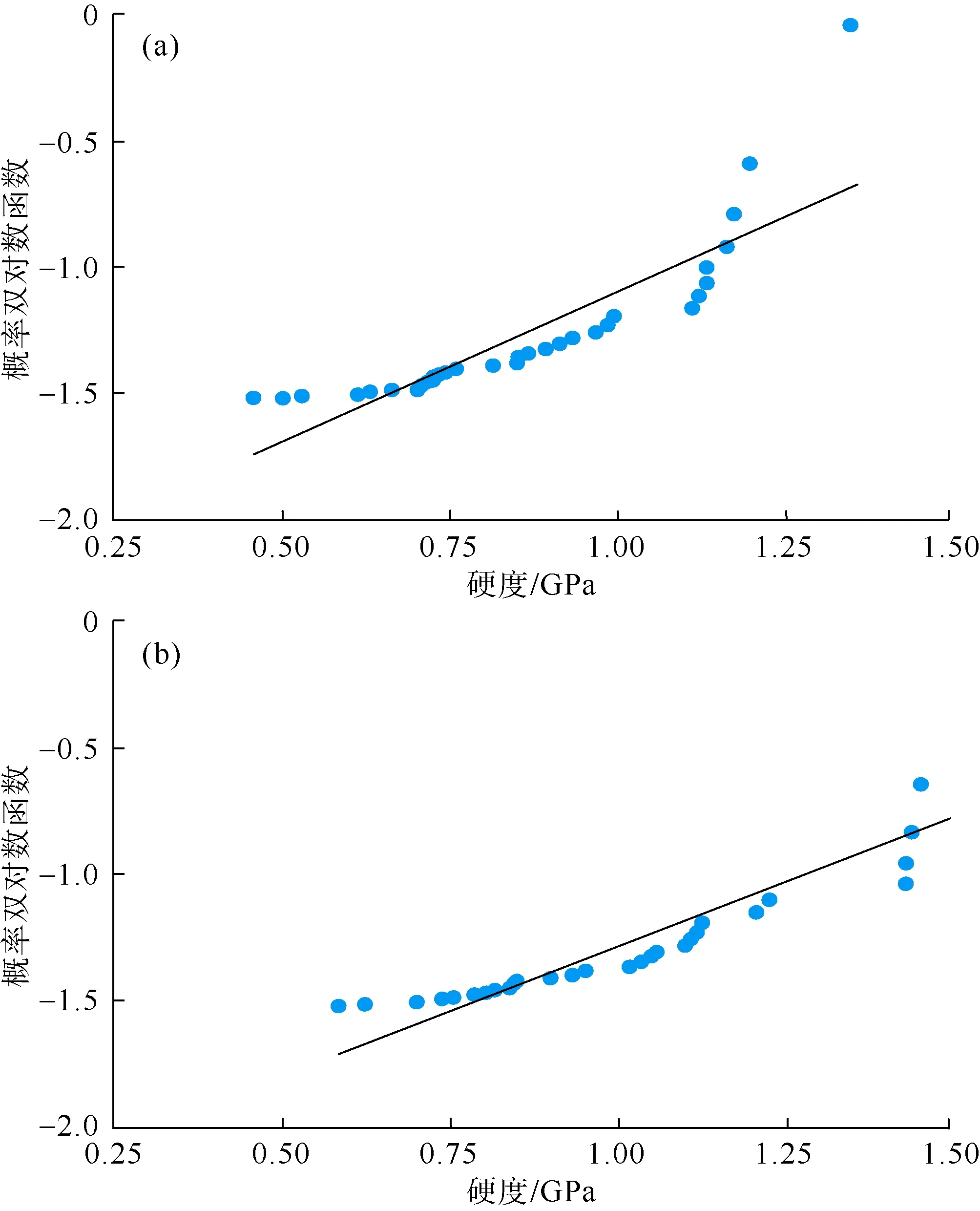
图8 平行层理（a）和垂直层理（b）条件下页岩硬度Weibull曲线

3.3 基于Mori-Tanaka模型的纳米压痕实验结果尺度升级方法

纳米尺度测试条件下，由于采取随机纳米压痕测试时极易打到不同的矿物上，造成测试结果出现离散，所以一般只有增加足够多的纳米测试点才可获取具有统计学意义的力学参数值。通过对不同矿物的纳米压痕测试结果分析可以看出，虽然整个试样不同矿物的力学性质差异较大，但在微观上可以将岩石按强度等级划分为由高强度矿物（白云石等）、中等强度矿物（石英、钠长石、方解石等）、低强度矿物（黏土、有机质等）等组成的三相介质力学模型（见图11），在纳米尺度下这三相介质可视为各向同性，根据不同介质体积分数并结合组分力学模型可得到纳米尺度向厘米尺度升级的等效力学参数。需要注意的是，黏土和有机质等低强度矿物内部可能存在纳米—微米尺度的微孔隙，求取等效力学参数时应考虑天然裂缝、微米及纳米孔隙等岩石内部缺陷对最后结果的影响。

图9 平行层理（a）和垂直层理（b）条件下页岩弹性模量Weibull曲线

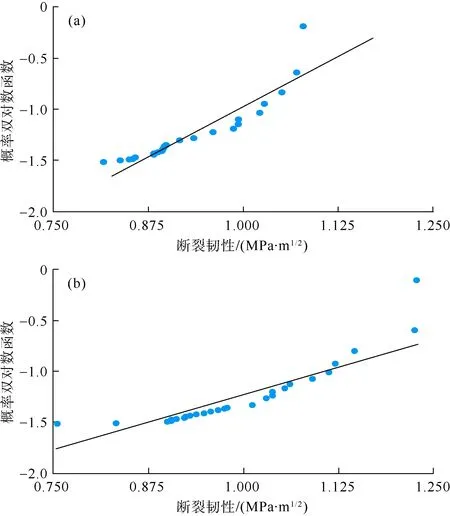
图10 平行层理（a）和垂直层理（b）条件下页岩断裂韧性Weibull曲线

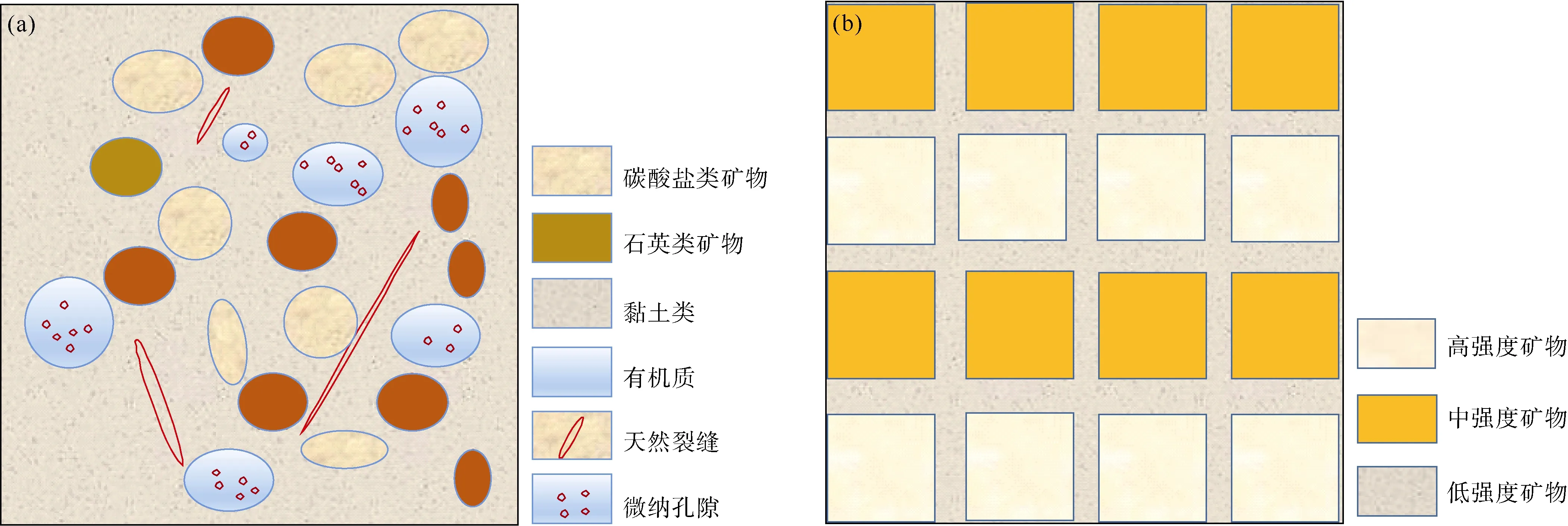
图11 岩石物理模型（a）转换为等效力学参数模型（b）

本文采用 Mori-Tanaka方法进行纳米压痕数据的尺度升级，各相介质的等效剪切模量和体积模量计算公式如下[22-23]：

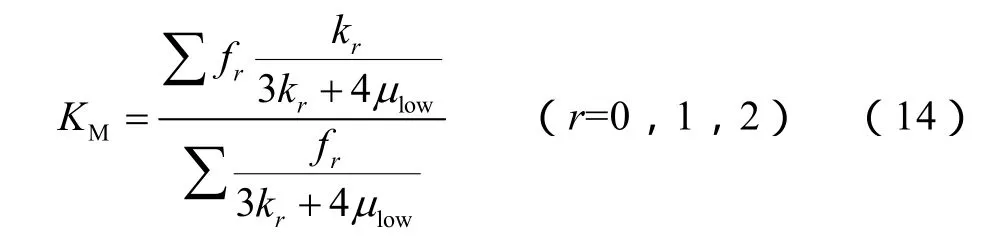
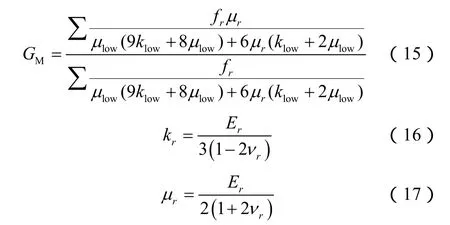
式中，r=0代表白云石等碳酸盐类矿物，r=1代表石英和钠长石等石英类矿物，r=2代表黏土类矿物。

高强度矿物和中等强度矿物力学参数可以通过纳米压痕数据结合EDS标定直接获取。考虑低强度矿物中微孔隙会对纳米压痕结果造成影响，获取低强度矿物等效力学参数时，需通过低强度矿物本身的孔隙度（本文实验取值3.5%）和压痕测试数据进行转化计算：

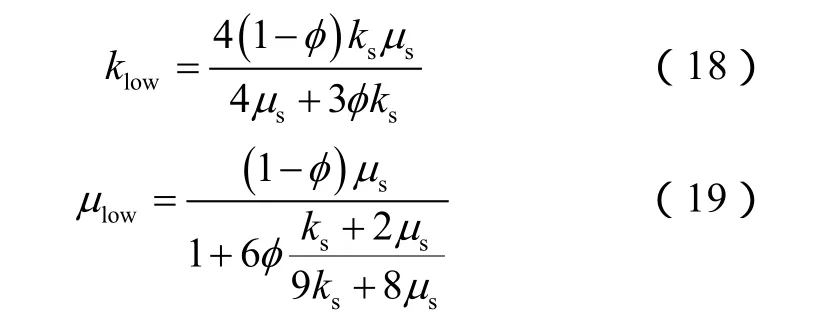
在得到三相介质等效力学参数后，可以通过下式计算厘米尺度下的岩石弹性模量：

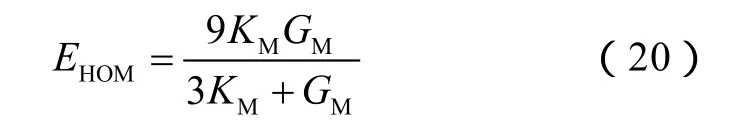
利用液压伺服刚性材料实验机开展单轴压缩实验，得到页岩单轴条件下的岩石应力应变实验结果，并以此计算弹性模量（见图12）。

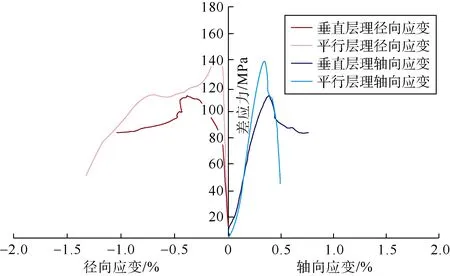
图12 页岩单轴压缩应力-应变曲线

通过 3种手段计算得到的岩石力学参数结果显示（见表5），组分升级力学模型计算值与岩心尺度单轴压缩获得的计算值有较好的一致性，而统计学纳米条件下力学参数值偏高，反映不同尺度差异下岩石力学性质的不同，根本原因在于实验试样尺度越大，试样所包含的微孔隙和裂缝数量越多，使得岩石受到外部载荷时，更易从微孔隙延伸成微裂纹，再扩展成宏观裂纹。采用组分力学模型则可减少压痕数量，实现与宏观力学参数对比验证，但却需要更加精细地刻画页岩表面矿物的分布和颗粒本身力学参数。

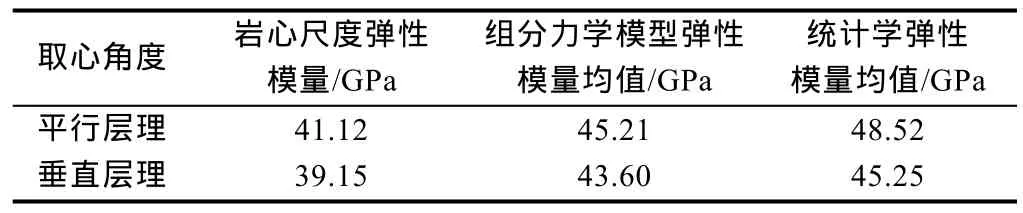
表5 尺度升级弹性模量分析结果

4 结论

针对 128个平行和垂直层理试样开展纳米压痕实验，应用载荷-位移曲线获得页岩的硬度、弹性模量、断裂韧性等参数，平行层理条件下的力学参数值要略高于垂直层理，弹性模量与硬度、弹性模量与断裂韧性之间存在较好的线性关系。

纳米尺度下力学参数测试结果具有一定的波动性且符合Weibull分布，其中硬度数据离散性最高。造成力学参数各向异性的原因一方面与页岩本身的非均质性相关，另一方面是在压痕实验过程中，强度较高颗粒会对裂缝延伸扩展造成阻力而影响最终结果，也与计算时仅引入投影面积作为参数相关。

利用BSE和EDS矿物解释结果对特定矿物力学参数进行纳米力学实验，提出基于高强度矿物、中等强度矿物、低强度矿物组成的页岩三相介质微观力学模型，采用Mori-Tanaka尺度升级方法进行组分力学模型计算，并同单轴压缩实验结果以及纳米压痕统计均值结果相对比，尺度升级结果与单轴压缩结果具有较好的一致性，但都较纳米尺度计算结果要小。岩石本身存在孔隙等缺陷导致不同尺度下岩石力学性质不同。

致谢：对中国科学院地质与地球物理研究所杨继进老师、杜忠明老师在实验方面提供的帮助表示衷心感谢。

符号注释：

Ac——相应载荷下的接触投影面积，m2；Amax——相应载荷下最大接触投影面积，m2；E——试样弹性模量，Pa；EHOM——厘米尺度下岩石等效弹性模量，Pa；Ei——Berkovich压头弹性模量，值为1 114 GPa；Er——不同矿物颗粒弹性模量，Pa；Er——折算弹性模量，Pa；fr——不同矿物颗粒体积分数，%；Gc——临界能量释放率，N/m；GM——体积模量，Pa；hc——接触深度，m；hf——残余深度，m；hL——保载点起始位移，m；hmax——最大位移，m；H——压入硬度，Pa；klow——低强度矿物等效体积模量，Pa；Kc——岩石断裂韧性，Pa·m1/2；KM——剪切模量，Pa；ks——黏土类矿物所占比例，%；kr——不同矿物颗粒体积模量，Pa；m——Weibull模数，无因次；pc——接触载荷，N；pmax——接触最大载荷，N；Pw——不高于随机变量的概率；S——接触刚度，N/m；Uc——裂缝断裂能量，N·m；Ue——弹性能量，N·m；Uir——不可逆能量，N·m；Upp——纯塑性阶段所耗失的能量，N·m；Us——纳米压痕绝对能量，N·m；Ut——总裂缝能量，N·m；X——随机变量；X0——随机变量最小参数值；Xi——特征参数；β——与压头几何形状相关的常数；φ——页岩孔隙度，%；μlow——低强度矿物等效剪切模量，Pa；μs——黏土类矿物剪切模量，Pa；μr——不同矿物颗粒剪切模量，Pa；ν——试样泊松比，无因次；νE——弹性能量比，无因次；νi——Berkovich压头泊松比，值为0.77；νr——不同矿物颗粒泊松比，无因次；ε——常数，0.75。