以“讲”促学发展八年级学生直观想象的教学案例分析
2019-02-26钟利
钟利

摘要:直观想象是数学学科的六大核心素养之一,在平时的教学中教师会借助图形、模型、多媒体等辅助教学,但学生的直观想象能力并没有得到很好的提高。选取现行人教版八年级下册教材与直观想象能力直接相关的“一次函数与二元一次方程组”这一节内容,通过引导学生大胆地“讲”,老师“听”的形式,以“讲”促学,提高学生的直观想象素养。
关键词:直观想象;引导;以“讲”促学
《义务教育数学课程标准(2011年版)》指出:“学生要敢于发表自己的想法,勇于质疑。”“学会与他人合作交流”。《普通高中数学课程标准(2017年版)》中提道:“数学不仅是运算和推理的工具,还是表达和交流的语言。”直观想象素养是数学学科的六大核心素养之一,它借助几何直观和空间想象来感知事物的形状与变化,利用图形来帮助我们理解和解决数学问题的素养。直观想象主要包括利用数形结合描述问题,借助几何直观理解问题,运用空间想象解决问题。直观想象一直是初中老师教学上要突破的难点。在平时的教学中教师会借助图形、模型、多媒体等辅助教学,老师很难及时地对学生的直观想象素养进行评价。为了更好地了解学生的直观想象水平,及时调整下一节课的授课计划,在课堂上进行数学交流就成了老师了解学生学习水平的一种有效手段。数学交流主要以讲为主,通过讲思路、讲方法、讲易错点、质疑等表达自己对数学问题的认识和理解。作为老师,要尽可能调动学生大胆展示,鼓励学生大胆质疑,师生共同探讨,通过学生讲、教师听的形式促进学生学习,以期达到培养学生的直观想象素养的目的。
本文以一节数学课堂教学案例进行分析,谈谈以“讲”促学发展八年级直观想象的教学研究。
一、案例描述
这是笔者上的一節与贵州平塘县某中学通过交互智能录播系统开展的一场异地互动常态课,课题为人教版八年级下册“一次函数与二元一次方程组”。这节课需要学生的数形结合、空间想象能力,是一节典型的发展直观想象素养的课程,学生理解起来有一定难度。为了让学生理解一次函数与二元一次方程组之间的关系,笔者设计了如下教学过程,旨在学生自学探究后在老师的引导下能自己归纳出一次函数与二元一次方程组的关系。设计的探究环节如下:
1.对于二元一次方程x+y=3,它有_____个解,用含有x的代数式表示y=__________。
二元一次方程2x-y=3,它有__________个解,用含有x的代数式表示y=__________。
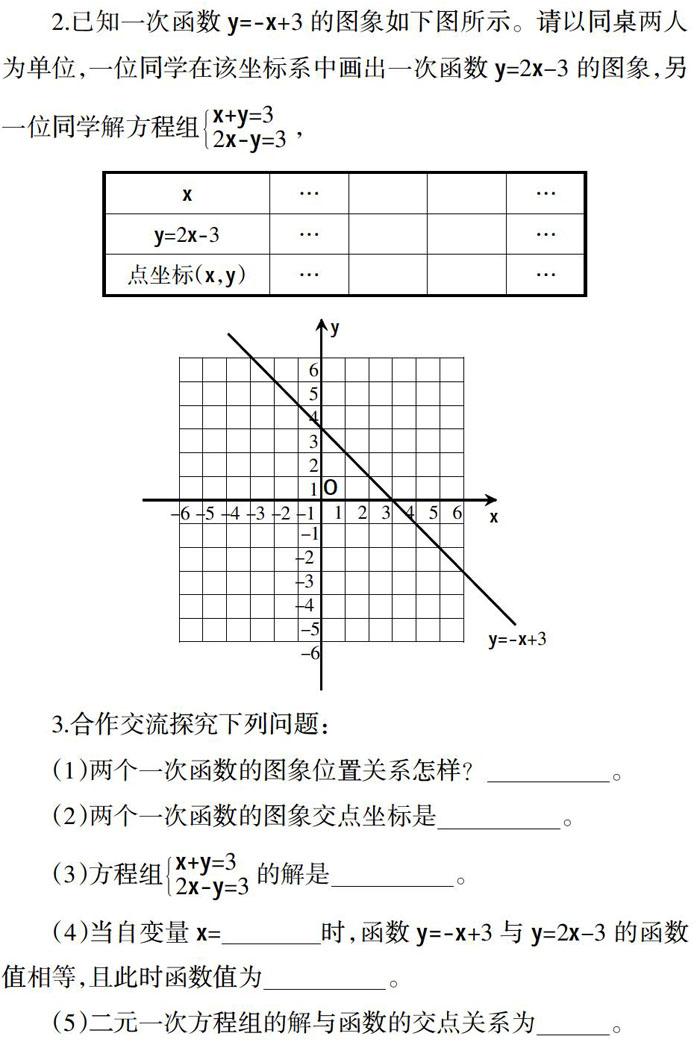
2.已知一次函数y=-x+3的图象如下图所示。请以同桌两人为单位,一位同学在该坐标系中画出一次函数y=2x-3的图象,另一位同学解议程组x+y=3 2x-y=3
3.合作交流探究下列问题:
(1)两个一次函数的图象位置关系怎样?__________。
(2)两个一次函数的图象交点坐标是__________。
(3)方程组x+y=3 2x-y=3的解是__________。
(4)当白变量x=__________时,函数y=-x+3与y=2x-3的函数值相等,且此时函数值为__________。
(5)二元一次方程组的解与函数的交点关系为__________。
在课堂上,笔者先让学生独立学习,接着再给时间让学生讨论,交流自己对一次函数与二元一次方程组关系的理解,最后请学生说一说自己的想法。当我提问:“一个二元一次方程有无数个解,请问这些解在平面直角坐标系里表示什么?”广州这边的A同学马上说:“点。”我接着问:“无数个点能组成?”贵州那边的B学生站起来回答:“老师,点动成线,所以无数个点组成一条直线!”我接着问:“通过刚才描点后,我们发现这些点组成了一条直线。我们知道,一条直线代表着什么函数?”A同学答道:“一次函数的图象是一条直线。同学们可以看我和同桌合作的这幅图(A同学上讲台利用几何画板再次画了图,无数个的点组成了一条直线,非常具体形象),从我们完成的这幅图,可以很清楚地发现,二元一次方程的无数个解与一次函数直线上的无数个点是成一一对应关系的,二元一次方程组有唯一的一组解,两条直线相交的时候也有唯一的一个交点,可见二元一次方程组的解就是直线的交点,反过来一次函数的交点坐标就是二元一次方程组的解。”这个时候我发现贵州那边的同学在交头接耳,看似有疑问,我立刻叫起一个C同学问道:“你们那边是不是有疑问?”C同学腼腆地说:“我们在想直线的位置关系是平行或相交,那两条直线平行的时候就意味着方程组无解,我们从来没见过方程组会无解,这到底是怎么回事?”C同学的问题让两边的同学顿时陷入了沉思,难道刚才的结论是错的吗?过了一会儿就听到D同学说:“老师,让我试试。”说完她来到讲台,徒手画了个平面直角坐标系,然后在上面画了两条平行的直线,分别是y=-x+3和y=-x+2,她解释说:“这两条函数表示为方程组是x+y=3 x+y=2,我发现只要x和y前面的系数比一样,后面的常数项的比不一样,这样的方程组是无解的,表示出来的函数图象就没有交点。而当方程组x和y的系数以及常数项的比相等时,如x+y=3 2x+2y=6,这个化简以后其实就是同一条方程,它有无数个解,这样的函数图象是两条重叠在一起的直线。”D同学从特例,结合图形分析得到一次函数与二元一次方程组的关系,可以看得出这个同学的直观想象能力是非常不错的。同学们也似懂非懂地明白了两直线平行重叠时与二元一次方程组的关系,这节课也算有不小的收获。
二、思考与分析
1."讲”能发展学生的直观想象能力
“用数学的眼光观察世界”是数学学科的顶层培养目标之一。什么是数学眼光?主要表现为数学抽象,而与数学抽象有着千丝万缕关系的是直观想象。直观想象是实现数学抽象的思维基础,数学的思维过程,即是在脑海中呈现所观察的图形,进而在脑海中思考,尝试运用各种方法解决问题,最终把它转化成书面的、有条理的语言。图形语言直观明了,有利于将问题具体化,帮助我们理解数学问题,书面语言严谨规范,则有利于数学问题的陈述。在数学教学中对学生进行图形语言与书面语言形式互化的训练,这不仅有利于学生对数学知识的理解,还有利于学生熟悉数学语言,为学生准确地用数学语言表达数学思维打下良好的基础。可见在课堂上训练学生用数学语言表达思维是可以发展学生的直观想象能力的。只有通过听学生讲,才能及时了解到学生的思维正确与否。鼓励学生讲思路,就如同鼓励小学生看图说话一样,先说一说,说完再修改,改完再说一次,直到说得条理清楚为止,慢慢地,经过训练后的学生写作文就只需要写个提纲就能洋洋洒洒地完成一篇佳作了。培养学生的直观想象能力也需要经过这样的过程,讲一讲,说一说,边讲边修改,思维得到训练,日积月累直观想象能力就能得到提高。
2.“讲”能让老师快速了解学生的所思所想
华罗庚教授曾教育中学生在数学表达上要“想得清楚,说得明白”。在日常与学生的接触中,我们发现学生听了未必听懂,听懂了未必讲得出来,而讲不出来的多半是写不出来的。学习金字塔也表明,单纯听老师讲的学习效率保持率只有5%,而讲给别人听,教别入学习的学习保持率高达95%。所以,数学课堂要重视学生讲、老师听这一环节。特别是直观想象的培养,我们借助图形、模型、多媒体等辅助教学,学生听得云里雾里不知所云,只有让学生在老师设置的问题引领下,学生通过讲思路、讲见解、讲方法,及时展示自己的思维过程,暴露自己的思维,才能便于老师了解学生思维到达的程度。这个时候老师给予适时的点拨,能收到事半功倍的效果。如这节案例一开始设计回忆二元一次方程根的情况,通过描点画图,直观感知一元二次方程与一次函数的关系,再给予时间让学生充分交流,最后在老师的问题引导下学生一步一步地归纳出一次函数与二元一次方程组的关系。这节课的设计与往常不同的是学生是主讲者,老师只是聆听者,听者有意,更能快速地收集学生思维的闪光点和不足之处,有针对牲地做出下一步指导。
3.“讲”得多能促使学生知识迁移
学习迁移是指一种知识的习得对另一种知识习得的影响,或已有的经验对完成其他活动的影响。知识迁移是学习的一种普遍现象,平时我们所说的“举一反三”“触类旁通”等即是典型的知识迁移形式。通过知识迁移,多种知识可以交汇,各种经验得以沟通。迁移在教学中发挥着至关重要的作用,进行数学交流就是要运用已有的经验与同伴交换看法,发表自己的见解,在数学课堂中,学生“讲”是必不可少的一个环节,讲的学生可以在自己原有的知识、经验上,通过讲,表述自己的看法、见解,同伴在聆听后质疑,提异议,这样双方都能在原有知识上发生知识的迁移。如案例中D同学的回答,得到两直线平行、重合时与二元一次方程组的关系,这些内容教材上是没有介绍的,也不在考试大纲范围之内,原本想着没有学生问起的话就不在课堂上涉及这个内容,但后来D同学的回答很好地促使同学们进行知识的迁移,进一步构建了直观想象。
三、结束语
我们一直致力于培养学生的直观想象素养,如何更有效地提高学生的直观想象能力,我们仍需努力。上述案例司空见惯,但从新课标提倡的课程理念来講,加强学生“讲”的数学交流方式是提高数学核心素养的一个有效手段。
参考文献:
钟进均.基于语言学视角的“说数学”探究[J].数学通报,2013(3).
编辑 王亚青
