“等效重力”思想的应用——从一道高考题说起

陈笃杰

(福建省漳州市第三中学 363000)

一、2018年全国Ⅰ卷第18题的探讨

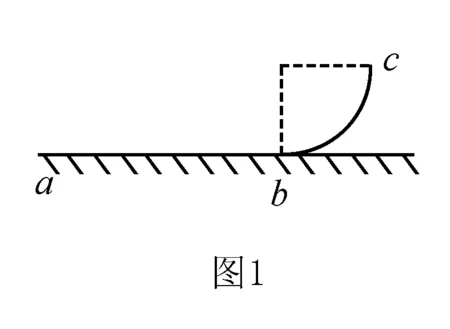
原题：如图1，abc是竖直面内的光滑固定轨道，ab水平，长度为2R；bc是半径为R的四分之一的圆弧，与ab相切于b点.一质量为m的小球始终受到与重力大小相等的水平外力的作用，自a点处从静止开始向右运动，重力加速度大小为g.小球从a点开始运动到其轨迹最高点，机械能的增量为( ).

A．2mgRB．4mgRC．5mgRD．6mgR

分析本题用很基本、简洁的物理模型来考查物理规律和思维方法，这也是全国卷命题的特点之一.学生对熟悉的物理情景容易上手，解题的关键是小球始终受到一个水平恒力，对文字表述“运动到其轨迹最高点”要细心审题，避免跳进“陷阱”.此题将运动的合成与分解、功能关系等核心考点有机融合，突出考查学生分析综合能力.

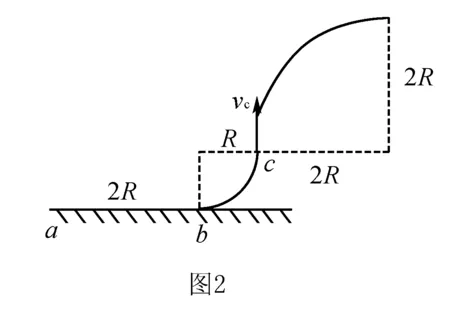
解法一设小球运动到c点的速度大小为vc，如图2，小球从a到c的过程中

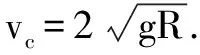
小球离开c点到轨迹最高点的过程中，由运动的分解得

竖直方向上：小球只在重力的作用下，速度从vc匀减速到0

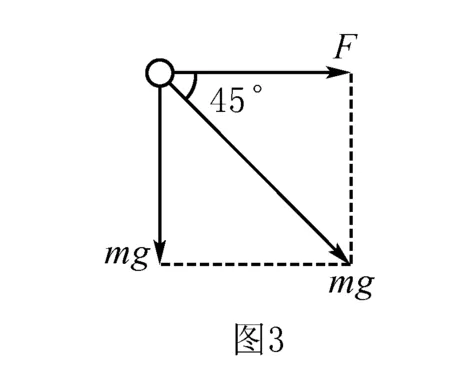
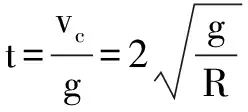
水平方向上：小球做初速度为零的匀加速直线运动，加速度a=g

小球从a点开始运动到其轨迹最高点的过程中，总水平位移大小为5R

由功能关系得：小球机械能的增加量ΔE=F·5R=5mgR

该解法中规中矩，要求学生具有扎实的基本功和一定的数学计算能力.然而作为一道选择题我们可以寻求较简捷的方法.

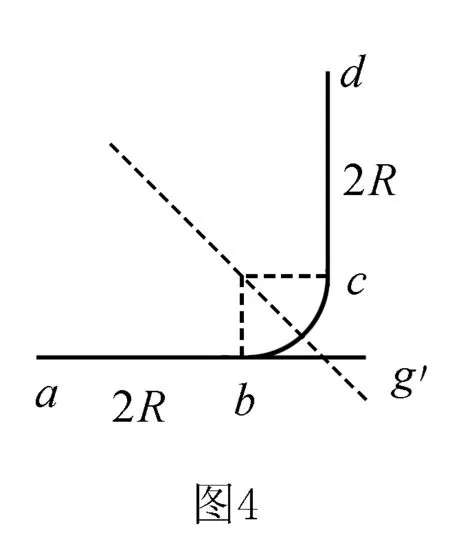
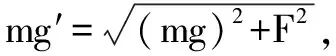
解法二我们可以设想，整个轨道模型处在一个与水平方向成45°斜向右下方的“等效重力场”中，四分之一圆弧的中点可称为“等效最低点”.如果在c点上方再补上一段竖直光滑轨道，如图4，从“等效重力场”的角度观察，呈现了我们熟悉的情景——“伽利略理想实验”的两个对接的斜面.根据对称性，小球从a点静止出发“沿斜面滚下”经圆弧后又会“沿斜面滚上”相同的“高度”，即恰好到达d点，cd=2R.

再撤去竖直光滑轨道，小球从c点抛出后，由于竖直方向上只受重力，按分运动的“独立性”可知，小球离开c点后到其轨迹最高点的竖直高度也为2R.又因水平和竖直方向上的两个分运动具有“对称性”，容易得出小球达到轨迹最高点时的水平位移也为2R，则从a点开始的水平总位移为5R，由功能关系得小球机械能的增加量ΔE=F·5R=5mgR.

解法二强调的是“物理思想”的应用，等效重力场确定后只要简单分析和推理，基本上无需数学计算就能快速得出结果，提高了解题效率.

下面以这道高考题为母题，通过一些简单的变形来探讨“等效重力”的应用.

二、一题多变、拓展延伸

拓展一在原题的基础上改为求：小球从c点抛出后经多少时间动能最小？最小动能为多少？

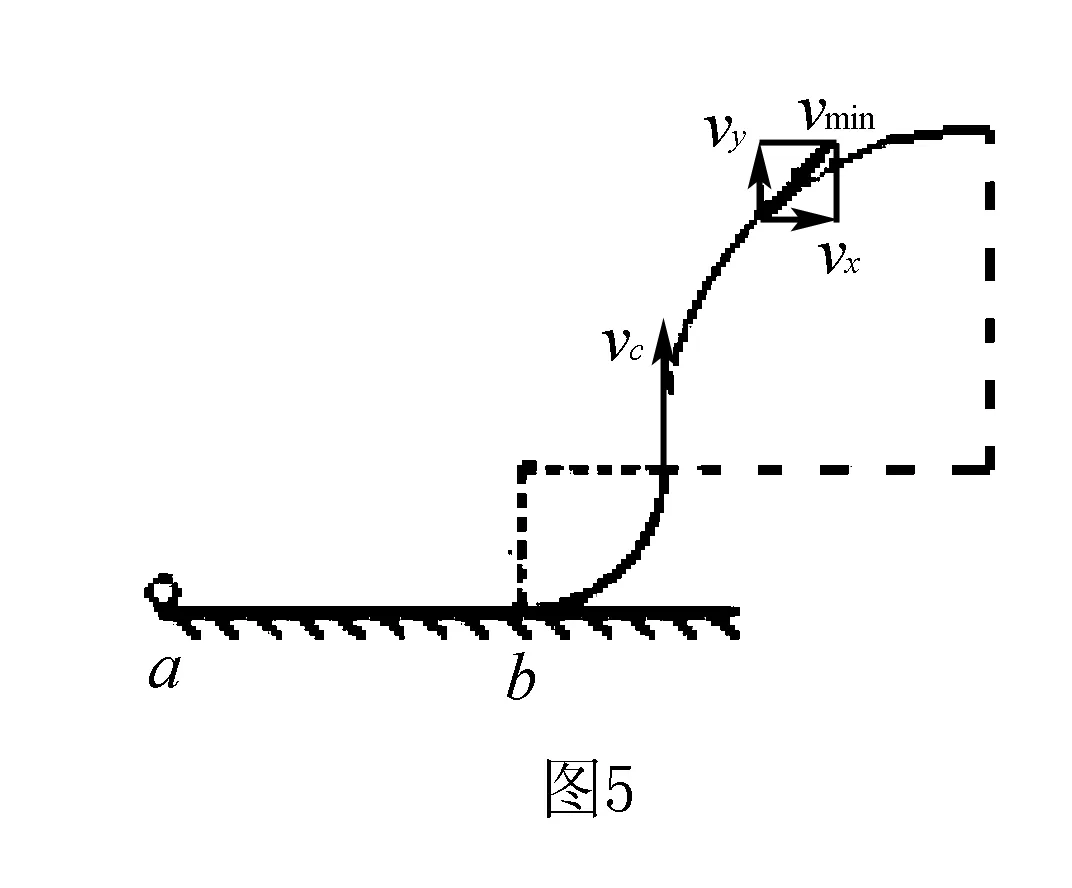
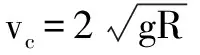
竖直方向上：做初速度为vc，加速度为g的匀减速运动

vy=vc-gt

水平方向上：做初速度为零，加速度为g的匀加速运动vx=gt

小球上抛后的速度

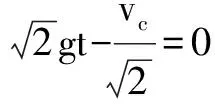
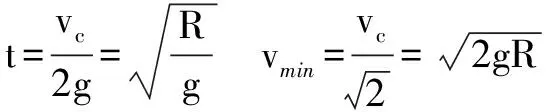
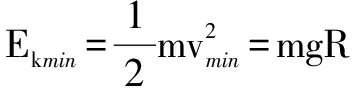
该解法运用二次函数求速度极值较繁琐，要求学生具备较强的数学能力.

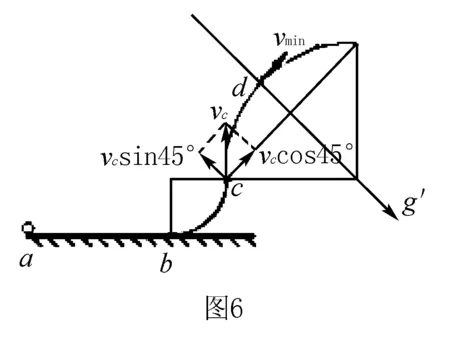
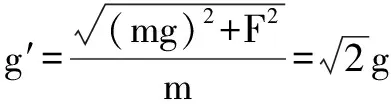
设小球斜抛到“等效最高点”d点的时间为t，有最小速度vmin

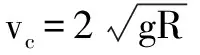
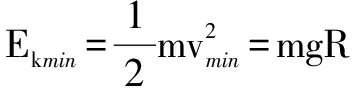
可见，解法二应用“等效重力”解题，思路清晰、过程简洁.

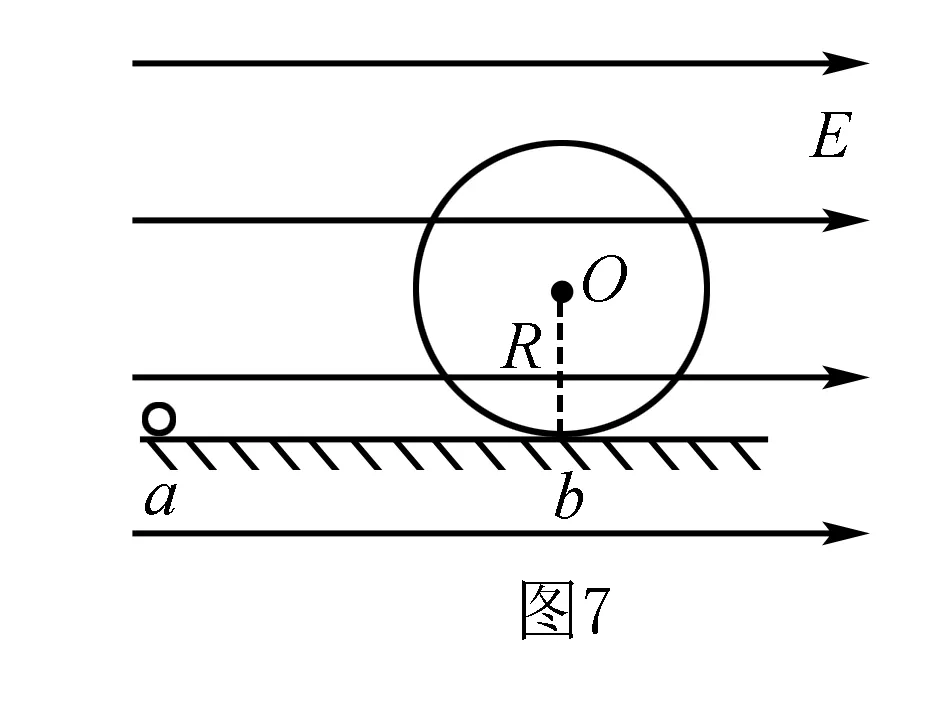
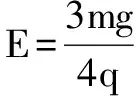
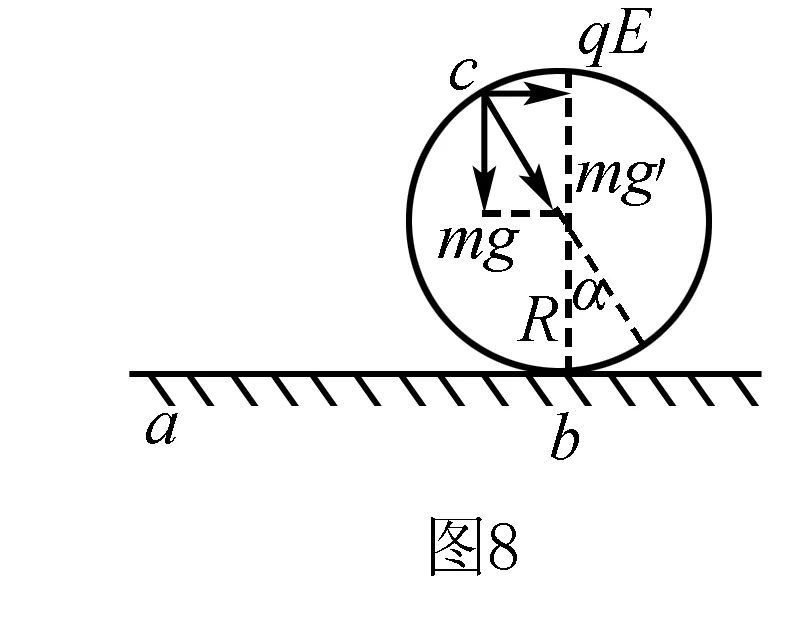
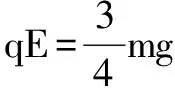
“等效重力场”(g′)与竖直方向夹角为α

设ab距离为S时,小球恰能做完整的圆周运动,小球在经过”等效最高点”c点时,对轨道压力恰好为零,即小球在c点只受”等效重力”mg′,cO方向与竖直方向夹角也为α.

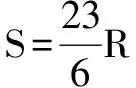
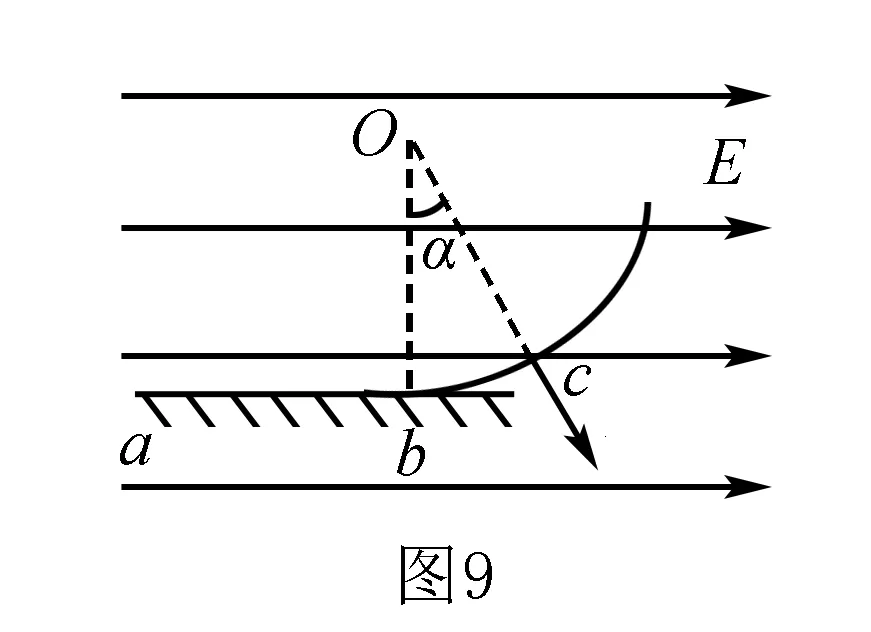
拓展三如图9,光滑的水平轨道和圆弧轨道在b点相切，整个装置处于一个水平向右的匀强电场中.带电小球在c点平衡,oc与竖直方向夹角α=30°.(1)要使小球运动到b点时速度为零,则小球由静止释放的位置与O连线与竖直方向夹角β为多少？

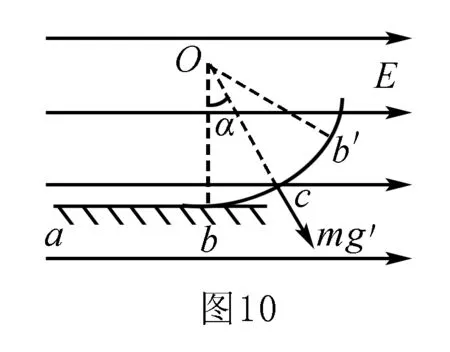
(2)若α≤5°，则小球从静止释放到达b点的时间为多少？

解(1)由于带电小球在c点平衡，可知c点为“等效最低点”，“等效重力”mg′方向沿Oc，如图10，根据对称性，小球应从c点右侧的b′点静止释放，b′点与b点关于Oc对称.因此，Ob′与竖直方向的夹角β=2α=60°，小球从b′点静止出发后将在bb′之间往复运动.

(2)若α≤5°，则小球将在bb′之间做简谐振动

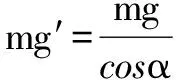
从静止释放后到达b点的时间

“等效重力”是等效思想在解题过程中的一种具体应用，是培养学生从不同角度思考问题能力的重要途径.我们可以利用类比法把一些复杂的、生疏的问题等效为我们熟知的、经典的重力场问题，使解题思路更加豁然开朗，减少繁琐的数学计算，达到“柳暗花明”的效果.

在重力场和匀强电场组成的复合场中，可应用“等效重力”处理的常见问题有：竖直平面内圆周运动的临界问题、单摆的对称性问题、求解抛体运动速度(动能、动量)极值的问题等.