数形结合在高中数学解题中的运用
2019-02-26王永辉
王永辉
(河北省石家庄市平山实验中学 050400)
一、数形结合思想
在数学中,我们学习和研究的知识,很多都是围绕数与形展开的,数与形存在着一定的联系,在部分特定的情况下,两者能够相互转化,我们能够在数形转化的过程中,加强对相关知识的理解与掌握.在高中数学解题过程中,我们能够通过运用数形结合思想,将解题思路清晰化,易化解题过程.数形结合思想,是在解题过程中,根据题目给出的条件与要求,同时思考题目内容的代数含义与几何意义,两者互相参考和印证,让相对抽象的代数含义以几何空间的形式直观地表现出来,或者用精炼的代数语言表达复杂几何空间形式的内容,让数与形紧密地联系起来.实际的解题中,数形结合思想,通常是将相对抽象的数量关系、数学语言与比较直观的几何位置、图形关系结合起来,通过代数来解析图形,或者通过图形来易化对代数关系的理解,让抽象复杂的形式简单化,从而更容易找出解题的方法与思路,提高解题效率.
二、数形结合思想的应用方法
在高中数学解题中数形结合的应用总体来说有三种方法,分别是以数转形、以形转数,以及数形互转.


第二,以形转数.虽然图形通常情况下都比较直观和形象,但数学很多时候都需要进行精确的计算和推导,仅靠图形来表达是不够的.解答相关问题时,我们可以利用以形转数的方法,将图形不足以表达的内容,通过代数来表示,然后再进行求解.例如,“已知不等式(x-1)2 在高中数学中,数形结合方法在很多题目中都能够得到良好的应用. 第一,数形结合在集合问题中的应用.例如,已知M,N为集合I的非空真子集,而且M与N不相等,如果N与M补集的交集为空,求M与N的并集.在求解这道题时,我们可以应用数形结合的方法构造图形(如图4),清晰地看出M与N以及I的关系,最终得出N为M的子集,M与N的并集为M. 第二,数形结合在函数问题中的应用.例如,设0 A.aa 在解题中,可以赋予a,b特定的值,然后画出图形(如图5),就能一目了然地得出结果为C. 第三,数形结合在解析几何问题中的应用.解析几何是高中数学的重点内容,也是数形结合运用的典型.解析几何的求解,都离不开数形结合思想. 在高中数学解题中,数形结合是一种非常良好的解题方法,能够有效帮助我们打开解题思路,提高解题速度,保证解题的准确性.在实际应用过程中,我们要把握数形结合的应用方法,判断数形转化的方式,充分发挥数形结合方法的作用,提高解题效率.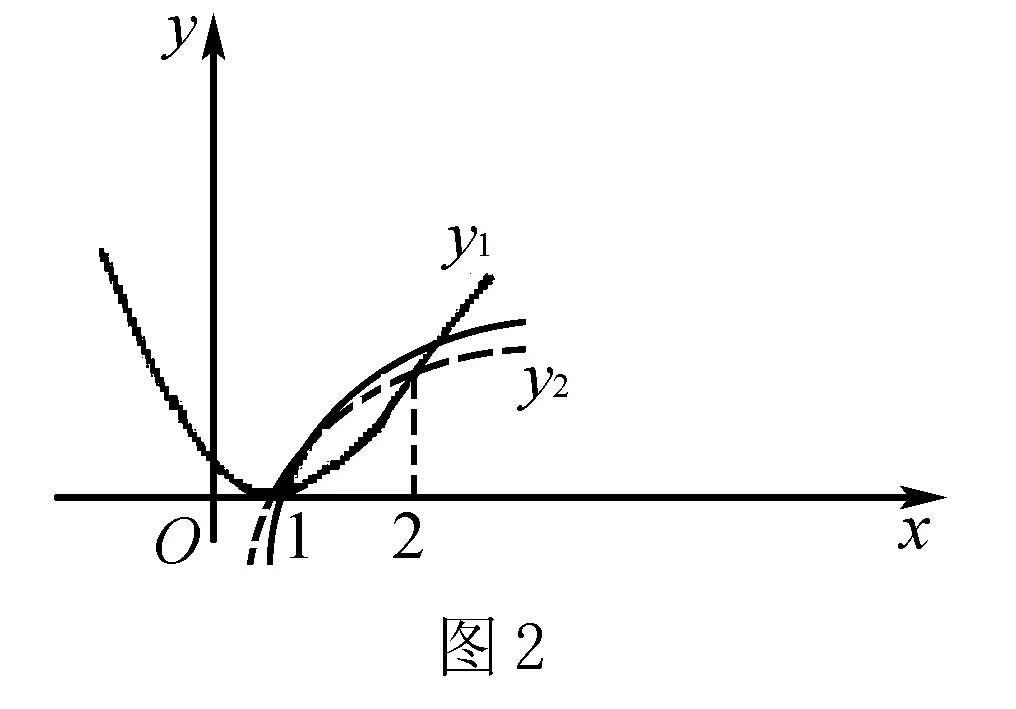


三、数形结合思想在解题中的应用