以正(长)方体模型为依托 巧解立体几何选(填)题

张桂华 沈加法

(云南省蒙自市第一高级中学 661199)

正(长)方体是点、线、面位置关系和数量关系的重要载体，正(长)方体模型是立体几何中的两个重要模型，以正(长)方体模型为载体研究和学习立体几何问题是新课标的要求.一方面，正(长)方体由于其图形本身对称完美，所含的线线、线面、面面的位置关系内容丰富，各种角度及距离均可在其中得以体现，堪称立体几何中的“万花筒”，是研究线线关系、线面关系、特殊几何体的重要载体.另一方面，许多立体几何的基本概念与定理可以在正(长)方体中得到反映，很多空间几何体可由正(长)方体切割而成，加之正(长)方体是学生在日常生活中最常见、最熟悉的一种几何体，如果教师在教学中能引导学生挖掘题设条件,展开联想、类比，引进旨在求解的辅助元素——正(长)方体模型,即将所求几何体补成正(长)方体或将其放入正(长)方体中，原几何体的一些位置关系和数量关系将会变得一目了然，学生将会增强对空间图形的变换与综合，许多立体几何选(填)题将能得到巧解，可收到事半功倍之功效.下面谈谈我在教学中引导学生解立体几何选(填)题的一些做法，仅供大家参考.

一、以正(长)方体模型为依托，将几何元素安插其中，对号入座，巧解立体几何选(填)题

例1 设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是( ).

A．若α⊥β，m⊂α，n⊂β，则m⊥n

B．若α∥β，m⊂α，n⊂β，则m∥n

C．若m⊥n，m⊂α，n⊂β，则α⊥β

D．若m⊥α，m∥n，n∥β，则α⊥β

分析本例中的线、面关系较为复杂，学生一时不易想象空间图形的位置关系，作图也相对较难，但若注意到4个选项中涉及的两条直线或两个平面不是垂直就是平行，如能以正(长)方体模型为依托，将题设中的线面关系放入正(长)方体中，对号入座，则各种线面关系将一目了然.

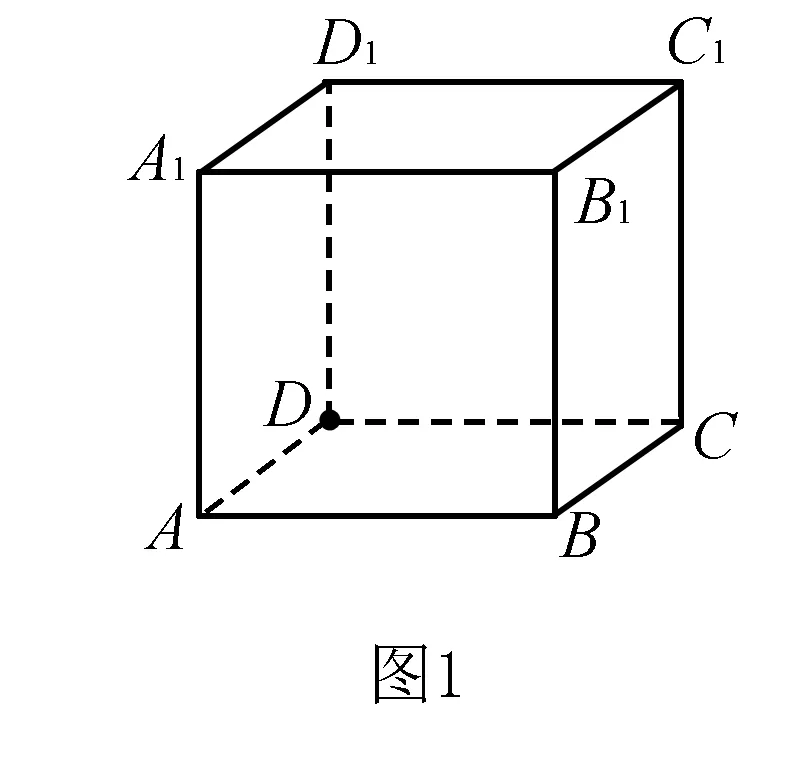
如图1所示：对于A：设平面ABCD为α，平面B1BCC1为β，设AD所在直线为m，B1C1所在直线为n，如图所示，显然有α⊥β，且m⊂α，n⊂β，但m⊥n不成立，故命题A不正确；对于B：设平面ABCD为α，设平面A1B1C1D1为β，设AD所在直线为m，D1C1所在直线为n，显然有α∥β，且m⊂α，n⊂β，但m∥n不成立，故命题B不正确；对于C：设平面ABCD为α，设平面A1B1C1D1为β，设AD所在直线为m，D1C1所在直线为n，显然有m⊥n，但α⊥β不成立，故命题C不正确．综上所述，故选D．

例2 在空间四边形ABCD中，AB⊥BC,BC⊥CD,CD⊥AB，且AB=BC=CD，则AD与BC所成角的正切值为____.

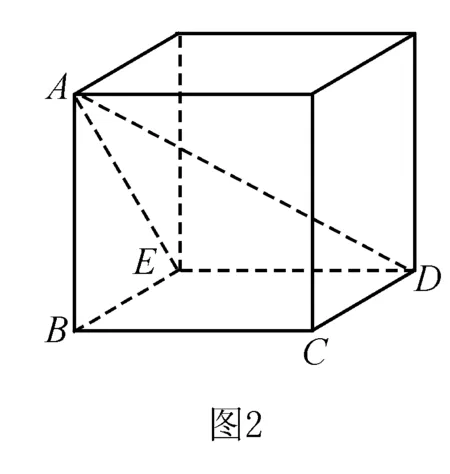
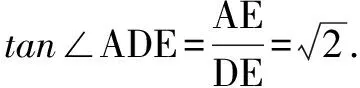
例3 已知直线a和平面α、β，α∩β=m，a⊄α，a⊄β，a在α,β内的射影分别为直线b和c,则b,c的位置关系是( ).

A．相交或平行 B．相交或异面

C．平行或异面 D．相交，平行或异面

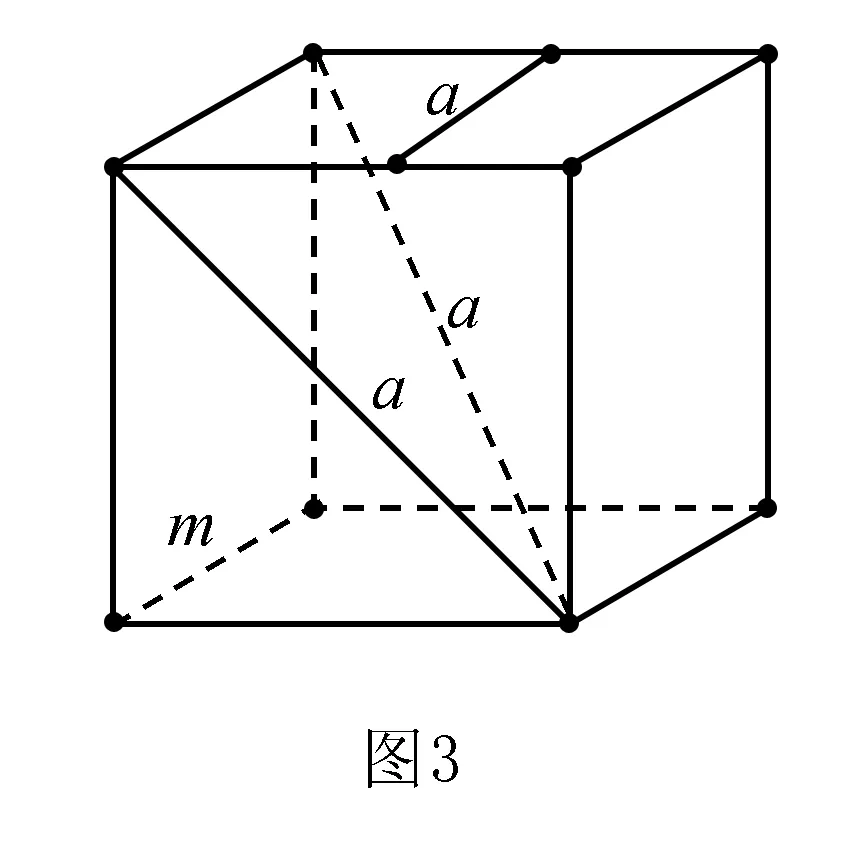
分析本例中的线、面关系较为复杂，学生不易想象空间图形的位置关系，作图难度较大，但若能以长方体模型为依托，将题设中的线面关系安插长方体中，对号入座，则各种线面关系将一目了然.如图3，构造符合题条件的长方体，将动直线a放入如图所示的3种位置，不难看出射影b和c有3种位置关系：相交，平行或异面.故选D．

例4 到两互相垂直的异面直线的距离相等的点( ).

A．只有1个 B．恰有3个

C．恰有4个 D．有无穷多个

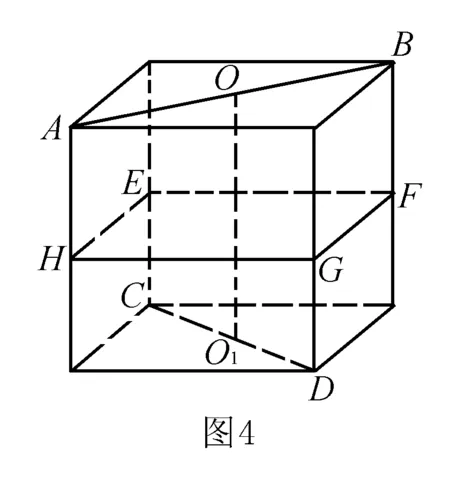
分析本题对学生来说较为抽象、复杂，难度较大，但若能以正方体模型为依托，将题设中的线线关系安插正方体中，对号入座，问题就会变得直观.如图4所示，显然，线段OO1、EF、FG、GH、HE的中点到两垂直异面直线AB、CD的距离都相等，所以排除A、B、C，故选D．

小结：涉及空间想象能力的一些线线、线面和面面位置关系的立体几何选(填)题，常可以正(长)方体模型为依托，运用正(长)方体中的线、面来验证或找出反例.

二、以正(长)方体模型为依托，在正(长)方体中构造棱柱、棱锥，可增强几何直观，进而发现几何体间固有的依存关系，巧解立体几何选(填)题

荷兰数学教育家弗赖登塔尔说：“数学是在内容和形式的相互影响之中的一种发现和组织活动.”从形式上看，棱柱、棱锥等几何体与正(长)方体模型无关，但从内容上看，垂直、平行，共球等性质却是这些几何体都共同具有的，因此，我们应善于从不同几何体间的相互影响之中来发现他们的内在联系，进而有目的性地组织我们的解题思路.

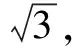
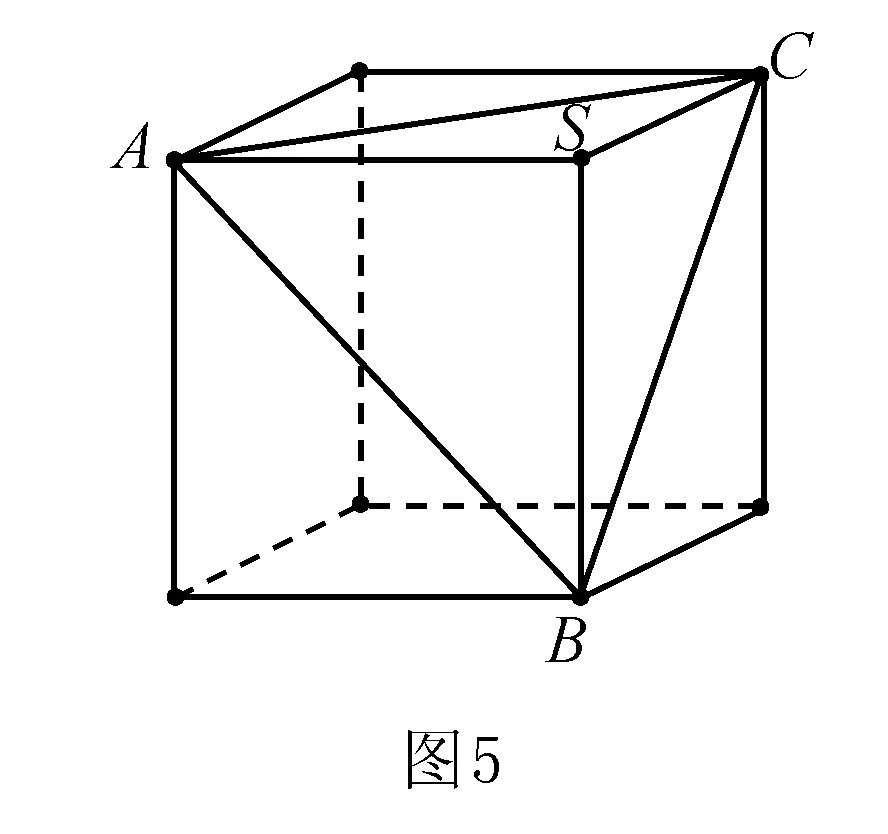
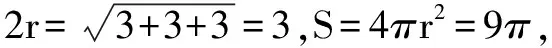
例6 在四棱锥的四个侧面中，直角三角形最多有____个.

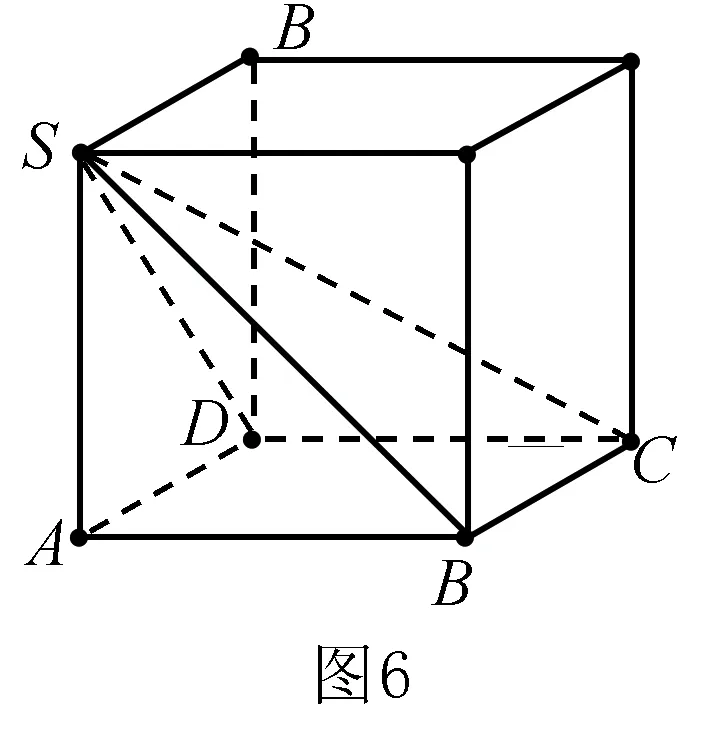
分析有2个直角三角形学生容易想到，但最多有几个就很难想了，靠推理论证似乎题设条件太少，也显得有些小题大做.但如能以正方体模型为依托，在正方体中构造如图6所示的四棱锥S-ABCD，则不难证明四个侧面均为直角三角形，故有4个.

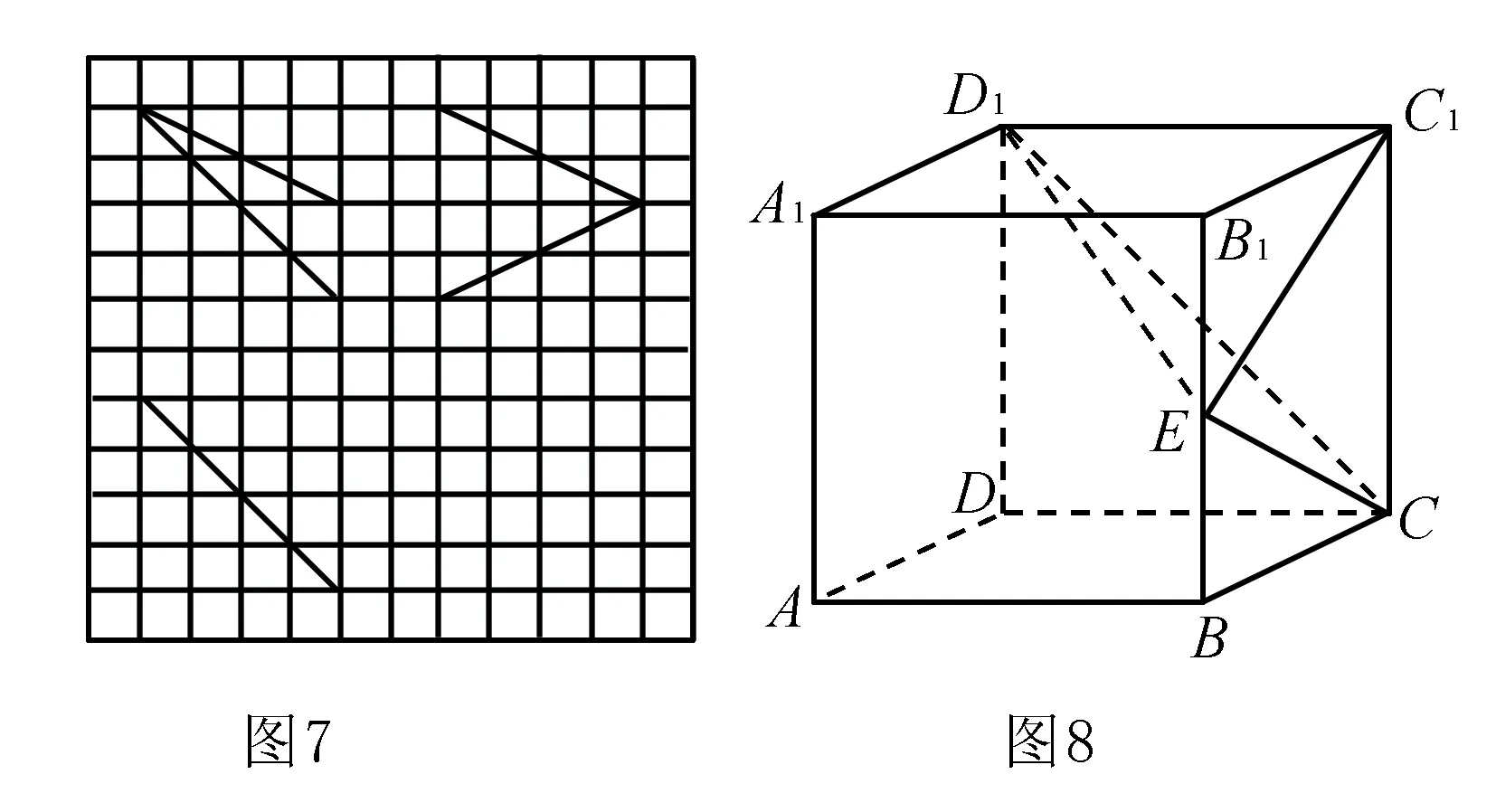
例7 如图7，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( )

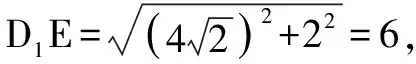
例8 如图9，已知正三棱锥S-ABC的侧棱与底面边长相等，E，F分别为SC，AB的中点，那么异面直线EF与SA所成角为____.

分析本例中通过中点作平行线，找到异面直线所成角困难较大，其次要熟悉正三棱锥的对棱互相垂直这一隐含性质，否则，解决本题确有一定难度，但若能以正方体模型为依托，在正方体中构造如图10所示的正三棱锥S-ABC，则容易看出SA与SD的所成角即为异面直线EF与SA所成角，显然∠ASD=45°.另外，我们还可直观地看到：正三棱锥的对棱互相垂直这一性质.

小结：棱柱、棱锥不是孤立的几何体，它和正(长)方体有着千丝万缕的联系，若能以正(长)方体模型为依托，把棱柱、棱锥放入正(长)方体中，不仅能彰显事物间的本质联系，所求问题会变得直观，解决问题的途径自然也就多了.

三、以正(长)方体模型为依托，化抽象为直观，把解决多面体与球的有关问题与正(长)方体联系起来，巧解立体几何选(填)题

由于正方体的特殊性，它存在一个外接球和一个内切球，因而有关多面体与球的诸多几何问题可以通过正方体模型来解决.

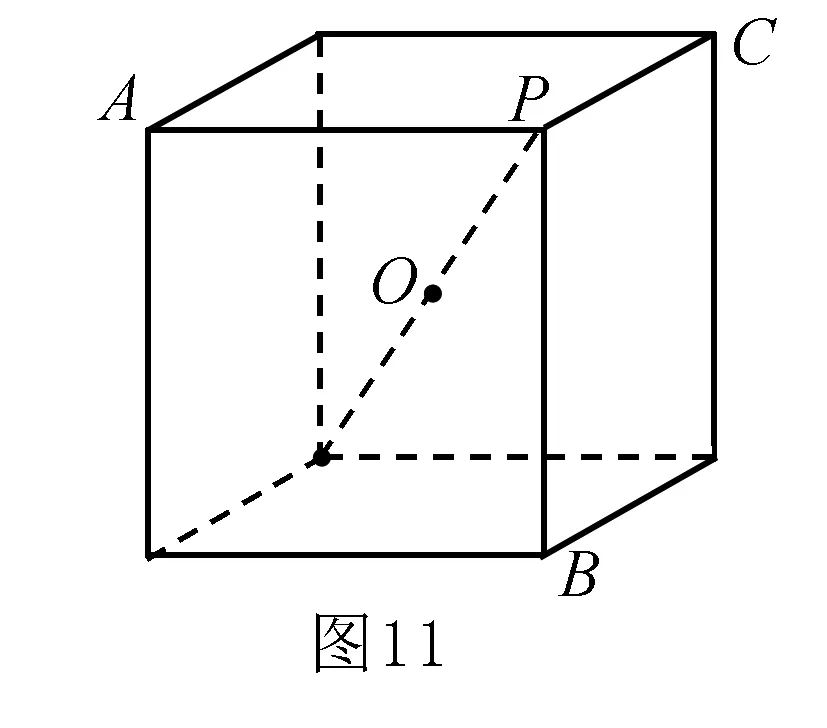
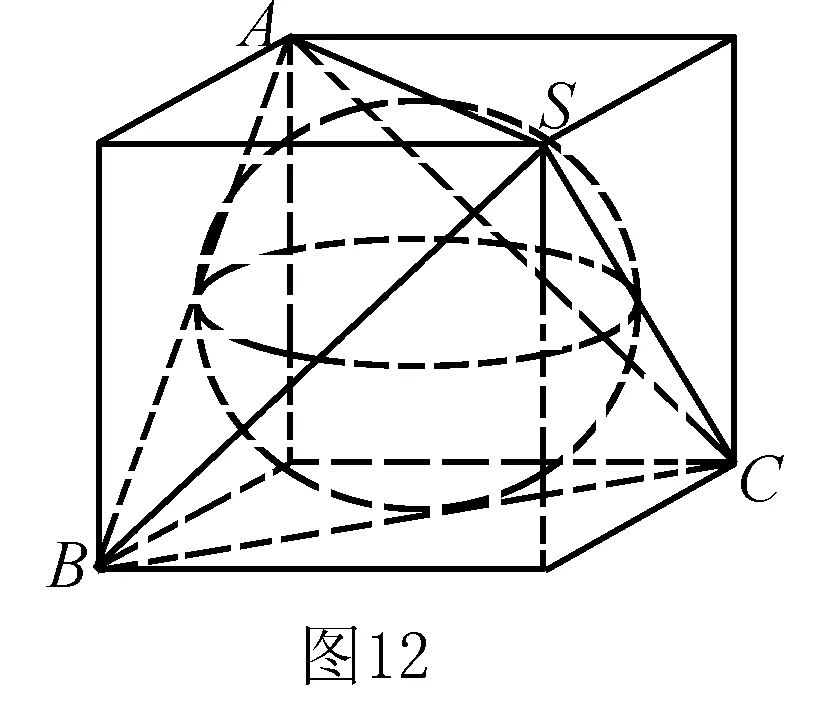
例9 已知点P，A，B，C均在同一球面上，如果PA，PB，PC两两互相垂直，且PA=PB=PC=a，则这个球的表面积为____．

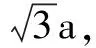
例10 已知一个正四面体的棱长为a,有一个球和它的六条棱都相切，则这个球的体积为____.

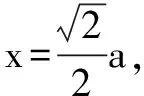
小结：由于画与球相关的几何直观图难度较大、给解题带来了困难，所以解决多面体与球有关的几何问题时应以正(长)方体为模型，将其进行等价转化，不要在画图上浪费时间，我们要做到“不画球，但心中有球”. 并且还要善于从不同几何体间的相互影响中来发现他们的内在联系，进而有目的性地组织我们的解题思路，从而使多面体与球的有关问题得以巧解.

总之，在立体几何解题教学中若能以正(长)方体模型为依托，是对“数学是一种发现和组织活动”，“数学是一种创造性过程的归纳科学”的实践检验.立体几何试题由于线面关系复杂,加之部分学生空间想象能力弱，因而对立体几何的学习往往感到畏惧.如果教师在教学中能引导学生挖掘题设条件,展开联想、类比，引进旨在求解的辅助元素——正(长)方体模型，即若能以正(长)方体模型为依托，将所求几何体补成正(长)方体或将其放入正(长)方体中；或在正(长)方体中构造棱柱、棱锥，增强几何直观，进而发现几何体间固有的依存关系，化抽象为直观；或把解决多面体与球的有关问题与正(长)方体联系起来，这样原几何体的一些位置关系和数量关系将会变得一目了然，学生将会增强对空间图形的变换与综合，许多立体几何选(填)题将能得到巧解，进而可收到事半功倍之功效.