一个高维非线性方程的黎曼theta函数周期波解

郭婷婷

(山西大学 商务学院， 山西 太原 030031)

0 引 言

在许多工程和科学技术领域中会遇到非线性波动现象， 例如光纤维学、 孤子理论、 流体力学、 混沌理论等[1]， 研究这些学科领域中的非线性模型显得尤为重要， 而求解这类方程的精通解则是研究学者主攻的研究方向之一. 现阶段已经成熟的求解方法有Lie群方法、 Darboux变换法、 代数几何方法、 Hirota方法等[2-6]. 其中代数几何方法是在反谱理论和代数几何理论的基础上发展起来的， 其最先对KdV方程进行研究， 到20世纪 70 年代， 这一理论发展为对包括KP方程、 Toda Lattice方程在内的一类孤子方程进行求解[7]， 而黎曼平面定义了这种拟周期波解的主要物理特征， 包括波的数目、 波速、 波的振幅. 但是运用代数几何方法较难直接确定波的这些特征参数. 20世纪80年代， Nakamura给出一种方便地构造非线性方程拟周期解的方法， 并运用该方法获得了KdV方程和Boussinesq方程的周期波解. 马文秀通过对一类(2+1)维Hirota双线性方程进行研究， 构造出这类方程的周期波解. 本文将涉足高维偏微分方程， 通过分析一般的黎曼theta函数及其周期性， 充分运用Hirota双线性方法， 将一个非线性的(3+1)维偏微分方程[8]双线性化， 并求出其单孤波解和双周期波解， 分析这两种解的参数之间的关系， 并对该方程双周期波解的渐近性态进行研究.

一般的黎曼theta函数[9]定义如下，

式中：β为复位移变量；φ，ψ为复参数. 黎曼theta函数是一个周期函数[10]，v>0是其周期矩阵， 因为L(β+1+iv,v)=exp(-2πiβ+πv)L(β,v)， 所以向量iv和1是该theta函数的周期， 具有1和exp(-2πiβ+πv)两个乘子.

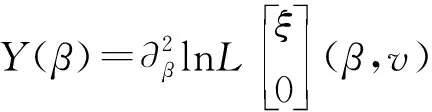
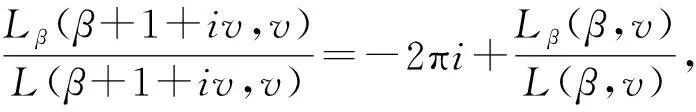
∂βlnL(β+1+iv,v)=-2πi+∂βlnL(β,v),

等号左右两端同时再对变量β求导， 得

即Y(β+1+iv)=Y(β), 所以Y(β)是具有1和iv两个基本周期的双周期函数.

对于(3+1)维非线性偏微分方程

(φt+6φφx+φxxx)x+3φyy+3φzz=0,

(1)

函数φ是关于空间变量x,y,z和时间变量t的关系式, 首先进行因变量变换φ=(2lnF)xx得

[2(lnF)2x,t+6(2lnF)2x(2lnF)3x+(2lnF)5x]x+

3(2lnF)2x,2y+3(2lnF)2x,2z=0,

在方程的左右两端同时对x进行两次积分并取积分常量为C得

3(2lnF)2y+3(2lnF)2z=-C.

注意到Hirota双线性算子和对数函数偏导数之间的关系恒等式[11]

非线性偏微分方程(1)将转化为双线性形式

整理即为偏微分方程(1)的双线性型

F(x,y,z,t)=0.

(2)

将函数F(x,y,z,t)取为τ的无穷级数形式F(x,y,z,t)=1+τF1+τ2F2+o(τ2)， 代入双线性表达式(2)中整理关于τ的幂次项

F1·1)=0,

(3)

F1·F1+F2·1)=0,….

(4)

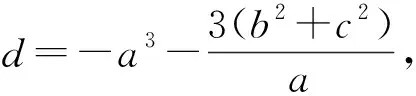
φ=2[ln(1+eα)]xx,

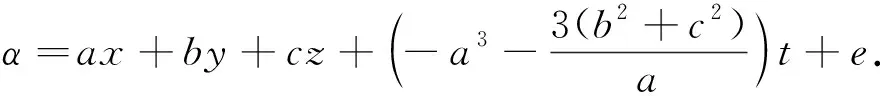
(5)

它在下文对该方程双周期波解的渐近性讨论过程中起到很重要的作用.

1 一个(3+1)维偏微分方程的双周期波解

e2πi(β+ξ′)q′-πvq′2·e2πi(β+ξ)q-πvq2=0.

(6)

由于双线性算子有如下运算性质[12]成立

(a1-a2)y1(b1-b2)y2…(c1-c2)y3(d1-d2)y4eβ1+β2,

βk=akx1+bkx2+…+ckxM+dkt+ek,k=1,2, 这里ak,bk,…,ck,dk,ek为常数, 那么式(6)将变形为

4π2(2q′-2p-μ)2fl+c]×exp{2πi(2p+μ)β+2πi[q′ξ′+ξ(2p+μ-q′)]-

当μ=0和1时， 上式等价于以下方程组

即

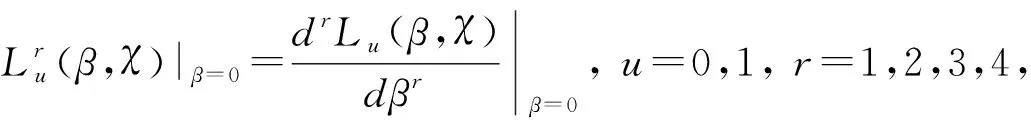
(7)

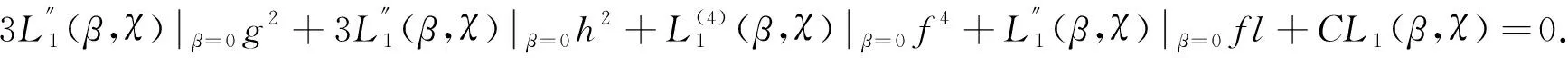
(8)

求解关于l和C的方程组得

(9)

2 一个(3+1)维偏微分方程双周期波解的渐近性态

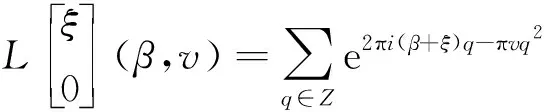
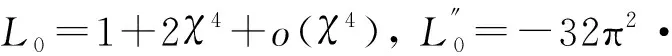
3 结 论