一种多约束指标改进的动态旅游路线规划算法
2019-02-23李胜辉高奎亮刘成龙王含巢胡家玮
周 啸, 李胜辉, 高奎亮, 刘成龙, 王含巢, 胡家玮
(1. 信息工程大学 基础部, 河南 郑州 450001; 2. 河南机电职业学院 信息工程学院, 河南 郑州 451191; 3. 信息工程大学 数据与目标工程学院, 河南 郑州 450001)
0 引 言
旅游者到达某个陌生旅游城市游览前, 需要掌握该旅游城市最具代表性或最感兴趣的景点信息, 特别是旅游地理信息和周边服务信息, 并提前规划出行路线, 以便在最短时间内花费最少旅行代价获得最佳旅游动机利益满足. 因此, 智能旅游路径规划是智慧旅游研究领域中的一项热门课题[1-3]. 旅游者对景点信息的掌握程度不一, 特别是一些对该旅游城市并不了解的旅游者, 他们通常借助智能推介系统选取旅游路线, 或者以旅行社、 旅游网站、 旅游书籍等推荐的路线为参考, 被动地接受已经规划好的路线, 个性化程度较低, 容易造成推介景点及路线不能满足旅游者个性化需求的状况, 降低旅游者获得动机利益的满足程度. 其中, 智能推介系统规划旅游路线时, 不能考虑旅游者对兴趣景点的偏好, 且通常仅以距离最短为目标, 综合考虑其他旅游地理信息较少, 推荐的最优路线可能并非旅游者认定的最优. 根据目前旅游路线规划现状, 需要解决以下两个问题, 一是推介景点应当不仅具有代表性, 还要最大程度地切合旅游者的兴趣需求; 二是以推介景点为基础规划最优旅游路线时, 要在距离最短的基础上充分结合与旅游者出行直接相关的城市服务系统, 最大限度提高旅游者满意度[4-5]. 本文构建了一种多约束指标改进的动态旅游路线规划算法, 该算法以兴趣景点和特征拐点集模型为基础, 结合城市旅游地理信息服务动态规划最优旅游路线, 实现旅游者个性化需求、 路线最短和便捷地理信息服务的结合, 最大限度满足旅游者动机利益.
1 兴趣景点集与特征拐点集建模
1.1 兴趣景点集与景点提取基底矩阵建模
1.1.1 兴趣景点集建模
智能旅游的一项核心目标是为旅游者制定动机利益最大化的个性化旅游路线, 以尽可能提高旅游者对制定旅游路线和方案的满意度, 提升旅游城市形象[6-8]. 规划个性化旅游路线以旅游者确定适合自身心理需求和旅行规划的兴趣景点为前提, 因此景点的分类和选取方法是关键. 为用户提供便捷的可视化景点选取平台, 是规划智慧旅游方案的重要前提. 以市区内景点为研究对象, 景点的分类准则不同[9-10]. 根据旅游者具体需求和景点自身属性, 此处给出景点分类准则及相关定义.
定义1 城市特征景点集Φ. 定义旅游城市市区空间范围内所有以智能机随机选取或旅游者主观提取为目的存在于智能机中的景点构成的集合为城市特征景点集, 以Φ表示.
定义2 城市特征景点子集Φi. 定义旅游城市市区空间范围内以某一准则R划分的城市特征景点集的子集为城市特征景点子集, 每个子集代表一类景点, 以Φi表示, 其中i∈(0,p]∈Z+,p为在准则R定义下城市特征景点的种类, 即城市特征景点子集数量, 其中p∈(0,maxp]∈Z+.
定义3 城市特征景点元素φj. 定义旅游城市市区空间范围内任意城市特征景点子集∀Φi所包含的任意单个景点∀Φj为城市特征景点元素, 以φj表示. 为区别不同城市特征景点子集Φi下的景点元素, 景点元素表示为
φj=Φi[φj].
(1)
定义4 景点分类准则. 定义根据旅游者年龄结构、 心理需求、 行程安排、 景点特征及其属性等因素划分景点的具体原则为景点分类准则. 对城市特征景点集Φ,p的取值越大, 景点分类越多. 而对城市特征景点子集Φi, 特征景点元素φj的数量由城市容纳的景点数量决定, 即对每一子集都有
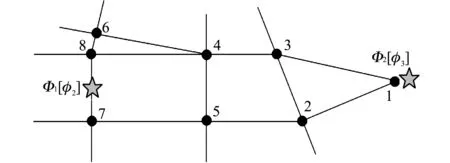
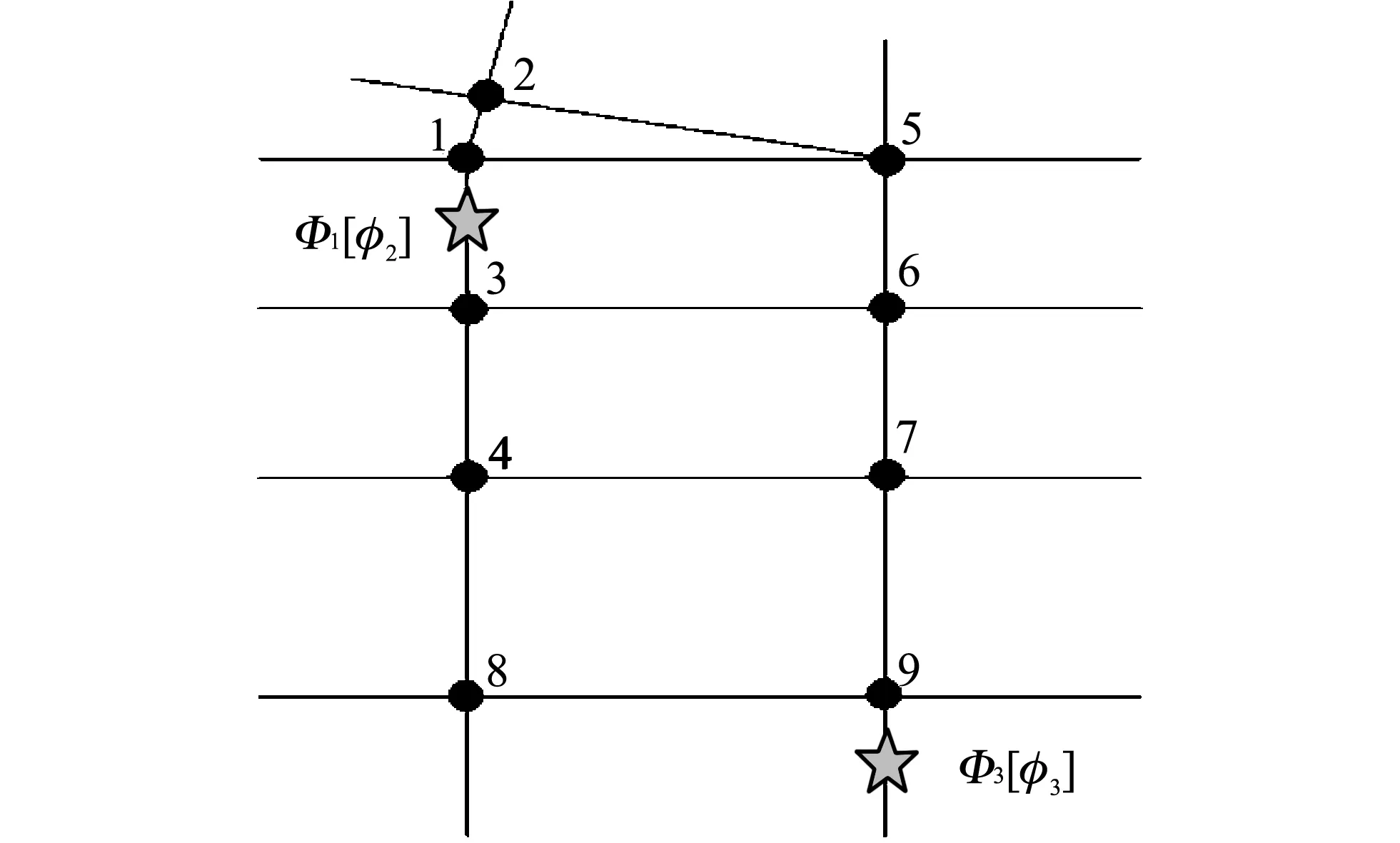
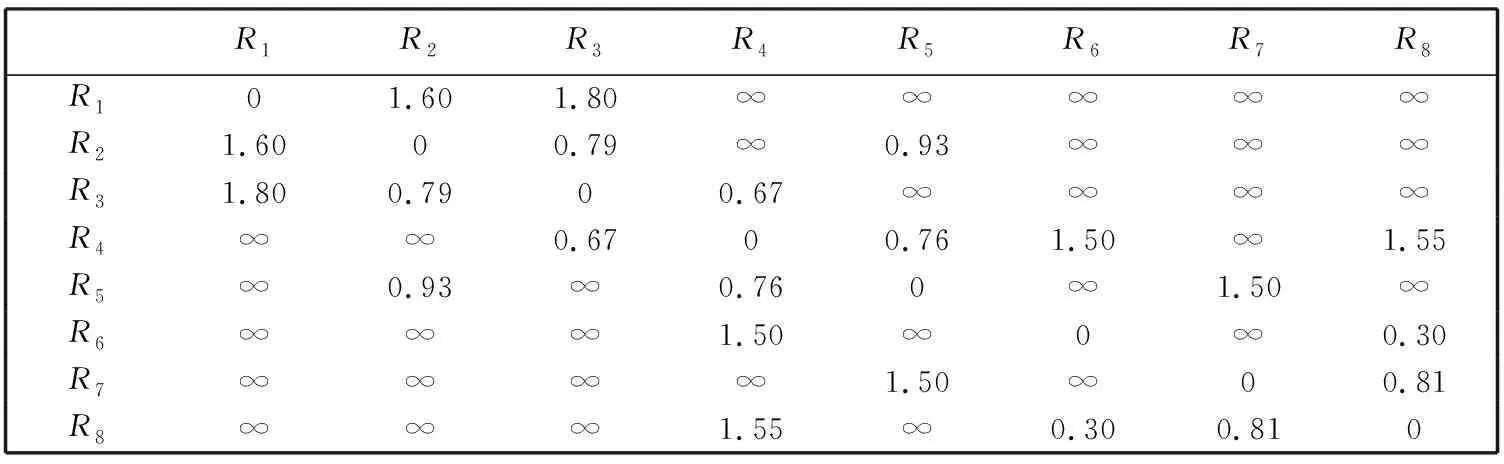
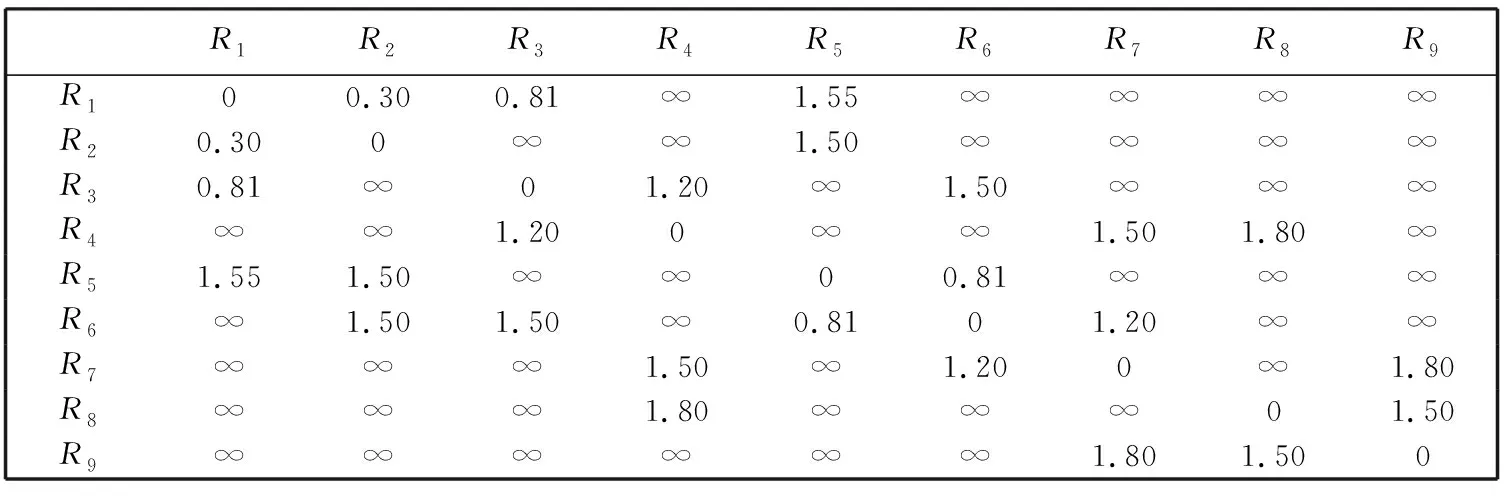
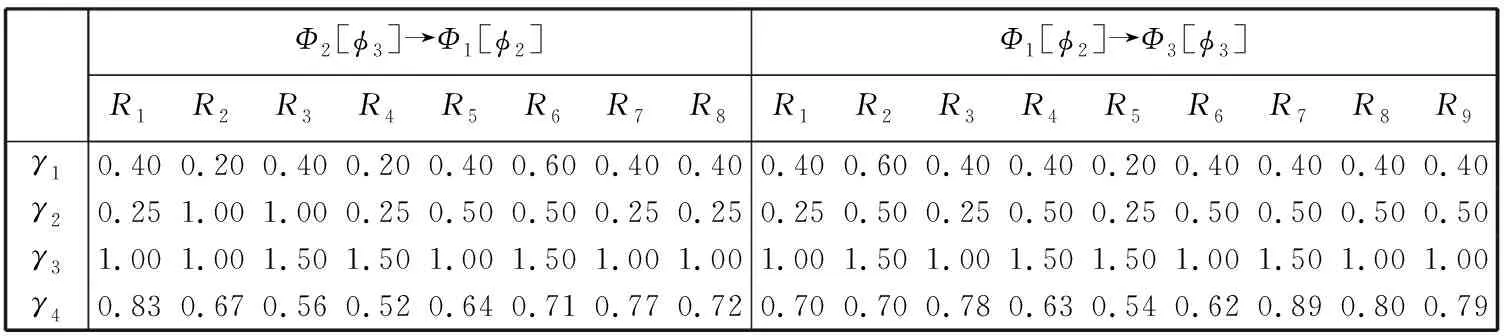
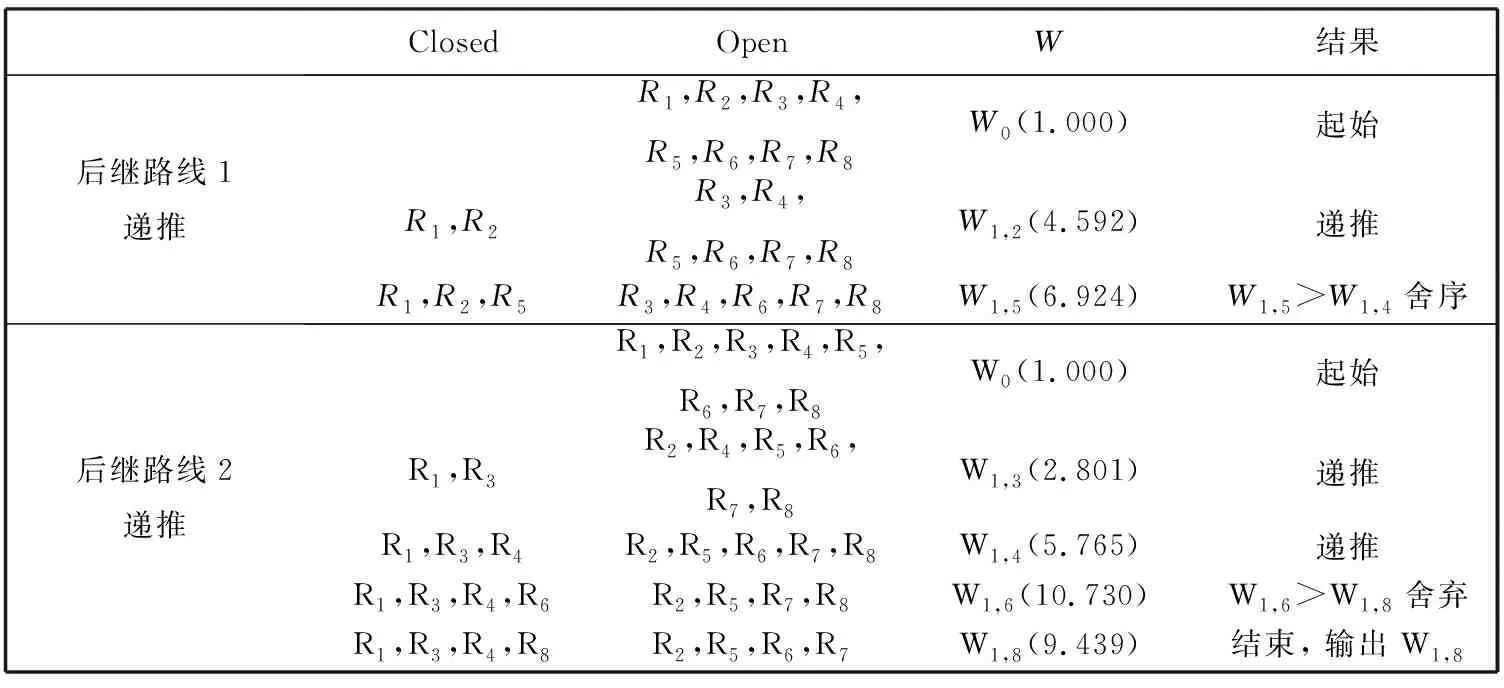
Φi={φj|Φi[φj], 0 (2) 1.1.2 景点提取基底矩阵建模 以城市特征景点集Φ及其子集为数据源构建景点提取基底矩阵A. 景点提取基底矩阵是智能机随机选取景点的数据矩阵. 当旅游者对城市景点情况不了解时, 向智能机提供希望游览的兴趣景点种类和数量, 智能机根据旅游者的年龄、 兴趣、 行程等随机选取特征景点后调用算法规划路线. 以特征景点子集构建景点提取基底向量A, 有 Ai=[Φi[φ1],Φi[φ2],…,Φi[φj]]. (3) 以p和景点提取基底向量构建maxp×maxj维矩阵, 矩阵第i行元素为子集Φi元素Φi[φj], maxj-j位取0, 则有景点提取基底矩阵A为 (4) 旅游者从一个景点游览摆渡到下一景点的过程中需经过街区和路口, 智能机选取最优街区和路口, 能给旅游者提供交通摆渡最佳体验, 获得动机利益满足[11-12]. 此处定义指标特征和特征拐点集. 定义5 特征指标因子γ. 定义道路枢纽指数γ1、 公交换乘站点系数γ2、 地铁换乘站点系数γ3和道路拥堵指标γ4等影响旅游者摆渡的因子为特征指标因子. 4项特征指标因子对旅游者选择摆渡路线、 获得动机利益满足有重要影响, 标准如下: 1) 道路枢纽指数γ1: 道路及道路节点在城市区域交通中的重要性系数. 根据道路重要性和街区通行能力, 将城市道路分为主干道路Path1、 次要道路Path2和辅助道路Path3. 主干道路或两条主干道路交点设γ1,1=0.20, 次要道路或主次道路交点设γ1,2=0.40, 辅助道路或两条次要交点设γ1,3=0.60, 次辅道路交点设γ1,4=0.80, 两条辅助道路交点设γ1,5=1.00. 4) 道路拥堵指标γ4: 一天内平均拥堵总时长n3(h)的倍数0.1n4. 定义6 特征拐点集R. 定义由智能机或人工选取的任意城市特征景点∀φj与其邻域内下一待游览特征景点φj+1之间具有特征指标因子γ的枢纽道路节点构成的集合为特征拐点集, 以R表示, 有 R={Rt|0 (5) 式中:Rt为特征拐点集元素, 代表某一具备特征指标因子γ的枢纽路口. 如图 1 所示, 景点φj和φj+1位于若干街区中, 满足特征指标因子γ的枢纽路口有maxt个, 数字代表t的取值. 按景点φj到特征拐点Rt之间的缓冲区半径r(φj,Rt)对特征拐点集元素升序排列, 有 R={Rt|R1,R2,…,Rmaxt}, (6) 式中:r(φj,R1)≤r(φj,R2)≤…≤r(φj,Rmaxt). 图 1 景点及其特征拐点Fig.1 Sight spot and feature spot 由图 1 可知, 旅游者从景点φj摆渡到景点φj+1需经过若干特征拐点, 每个特征拐点具备特征指标因子. 两景点间基于空间距离dis(x)迭代特征指标因子获得迭代值以确定最优旅游路线. 设disw,v,k为w点摆渡至v点过程中以集合K={k|0 1) 最短路径经过集合K中一点k:disw,v,k=disw,k,k-1+disk,v,k-1; 2) 最短路径不经过集合K中一点k:disw,v,k=disw,v,k-1. 则有:disw,v,k=min(disw,v,k-1,disw,k,k-1+disk,v,k-1). 若仅考虑路径长短, 不一定能满足旅游者动机利益, 应结合摆渡过程的实际地理信息服务需求. 此处定义动机迭代指标. 定义7 景点子区间动机迭代指标. 由任意景点∀φj与下一景点φj+1间特征拐点摆渡距离disw,v(km)和特征指标因子γ迭代输出的影响旅游者动机利益的指标值. 定义8 景点区间动机迭代指标. 起始景点和终止景点间多个景点子区间的动机迭代指标和. 根据节点摆渡距离disw,v和特征指标因子γ构建景点子区间动机迭代指标Wφj,φj+1和景点区间动机迭代指标W, 分别为式(7)和式(8). 其中Wφj为景点φj处的景点动机迭代初始值. (7) (8) 设景点φj与景点φj+1间包含k个特征拐点, 构建Open表和Closed表, Open表存放未扩展拐点, Closed表存放已扩展节点. 旅游者根据自身兴趣从景点提取基底矩阵A中以基向量所在行为单位提取m个待游览的特征景点. 当旅游者对城市景点不熟悉时, 也可根据特征景点种类提供游览景点数量, 由智能机随机选取m个特征景点. 首先研究起始景点到第二个景点间最优路线, 构建搜索算法: 1) 将t个特征拐点R1,R2,…,Rt放入Open表; 2) 选取距离景点φj最近的特征拐点R1并将其放入Closed表, 并从Open表删除. 搜索R1和R1后继邻近节点Ra1间距离dis1,a1, 以R1,Ra1及二者之间通路的特征指标因子γ迭代计算W1,a1; 3) 返回步骤2), 搜索R1另一后继邻近节点Ra2, 迭代计算W1,a2. 若W1,a2 4) 搜索Ra1的后继邻近节点Ra3和Ra2的后继邻近节点Ra4, 后继节点由城市道路分布和缓冲区半径r(φj,Rt)决定. 迭代计算Wa1,a3和Wa2,a4; 5) 由步骤4)迭代计算W1,a3和W1,a4. 若W1,a3 6) 返回第2)步, 继续搜索, 直到搜索到与目标景点φj+1邻近的特征拐点Rt为止, 输出动机迭代值W1,t最小的一条路线的maxW1,t. 算法各步骤, 满足ao∈(0,maxt]∈Z+,ao为R的序列脚标. 考虑旅游者年龄构成和景点特征, 取maxp=3, 则有maxi=3, 城市特征景点集Φ满足Φ={Φi|0 (9) 表 1 景点子集元素景点编码 由表 1,p1=7,p2=6,p3=7, 则maxp=7. 构建景点提取基向量A1=[Φ1[φj1]],A2=[Φ1[φj2]],A3=[Φ1[φj3]], 其中j1∈(0,7]∈Z+,j2∈(0,6]∈Z+,j3∈(0,7]∈Z+. 对景点提取基底矩阵补零后得式(9)景点提取基底矩阵A3×7. 图 2 景点Φ2[φ3]和Φ1[φ2]间通路与特征拐点集Fig.2 Path of sight spot Φ2[φ3] and Φ1[φ2] and feature spot set 图 3 景点Φ1[φ2]和Φ3[φ3]间通路与特征拐点集Fig.3 Path of sight spot Φ1[φ2] and Φ3[φ3] and feature spot set 表 2 景点Φ2[φ3]和Φ1[φ2]特征拐点摆渡距离disw,v(km) 表 3 景点Φ1[φ2]和Φ3[φ3]特征拐点摆渡距离disw,v(km) 表 4 特征拐点特征指标因子 由算法步骤1)~6)迭代计算Φ2[φ3]和Φ1[φ2]景点子区间动机迭代指标, 如表 5 所示. 由表可知, 从景点Φ2[φ3]到Φ1[φ2]输出动机迭代最小值为W1,8, 即经过拐点R1,R3,R4和R8. 同理, 动态递推景点Φ1[φ2]和Φ3[φ3]间动机迭代最小值为经过拐点R3,R4,R8和R9的W3,9. 综合表 5 递推结果, 从景点Φ2[φ3]游览至Φ1[φ2]最后到Φ3[φ3], 分别经过区间一的R1,R3,R4,R8和区间二的R3,R4,R8,R9能够输出最小动机迭代值, 由景点即所属区间拐点构成的路线为最优路线. 表 5 Closed表和Open表动态递推动机迭代值最小路线 本文在最优路线规划的基础上提出了一种多约束指标改进的动态旅游路线规划算法, 综合考虑区间距离最短、 道路枢纽指数、 公交站点换乘系数、 地铁站点换乘系数和道路拥堵指标等约束条件, 动态递推规划动机迭代值最小的路线为最优旅游路线. 算例证明, 该算法能够输出距离最短同时符合旅行摆渡过程一般规律的路线, 满足旅游者个性化需求, 使旅游者获得最佳动机利益满足.1.2 特征拐点集建模
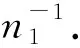


2 动态规划算法建模
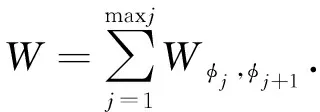
3 算例分析



4 结 论
