基于二维熵的快速SIFT图像匹配方法

马海波， 张鹏程， 张 权， 杨冠儒， 王 娜， 桂志国

(1. 中北大学 生物医学成像与影像大数据山西省重点实验室， 山西 太原 030051； 2. 北京工业大学 信息与通信工程学院， 北京 100124)

0 引 言

图像匹配作为数字图像处理领域的主要内容， 已被广泛应用于目标跟踪、 模式识别、 医学智能诊断、 影像分析等诸多领域中[1]. 图像匹配是指对一幅给定的图像(参考图像)的结构、 灰度、 特征等进行相似性和一致性分析， 在另一幅图像(待匹配图像)中寻找与之有相同特征信息的部分. 目前， 图像匹配方法分为两种： 一种是基于图像灰度的匹配方法， 另一种是基于图像特征的匹配方法. 而基于图像特征信息的匹配更加稳定， 所以基于特征点的匹配已成为近年来研究的热点[2-4].

1999年， Lowe提出了一种基于尺度不变特征变换的匹配算法， 即SIFT算法， 并在2004年对该算法进行了改进. SIFT算法不受图像旋转、 图像缩放、 亮度变化的影响， 而且具有对视角变化、 仿射变化、 噪声干扰也保持一定程度的稳定性等优点， 但存在匹配时间太长的问题[5-6]. 为了减少SIFT算法匹配时间， 大量学者做出相关研究并从不同角度提出了有效的改进方法. Herbert Bay等[7]提出了SURF算法， 将传统SIFT算法描述子的维度由128维降低到64维， 加快了图像的匹配速度. Ke Y等[8]提出了PCA-SIFT算法， 通过对特征描述子降维， 从而提高特征匹配速度. 刘辉等[9]提出了结合Canny算子， 剔除影响匹配的伪特征点以减少计算量， 从而提高匹配速度. 张永等[10]提出了一种基于内核投影的改进SIFT算法， 使特征描述子维数降低， 从而降低匹配时间. 林强[11]结合Harris角点检测的方法筛选特征点， 在速度上要快于传统SIFT算法. 张鑫等[12]提出了在特征点匹配时引入粒子群算法寻找极值， 可以加快匹配速度.

本文提出的算法主要在特征点提取与特征点匹配阶段进行改进， 采用结合图像二维熵[13-15]的方法加快匹配速度. 在特征点提取阶段计算特征点位置的二维熵， 剔除二维熵较大的特征点， 获得稳定的特征点. 在特征点匹配阶段， 计算参考图像中特征点与待匹配图像中特征点的二维熵差值， 若该值较小， 则这两点匹配； 若该值较大， 则这两点不匹配， 忽略该待匹配特征点， 继续在待匹配图像中寻找匹配的特征点， 这样可以减少匹配过程中欧氏距离的计算量. 相对于传统SIFT算法， 本文算法在匹配速度上有一定的提升.

1 SIFT算法

1.1 特征点提取

1.1.1 尺度空间极值检测

Lindeberg[16]通过实验证明高斯卷积核是尺度变化的唯一线性核. 尺度空间可表示为图像I(x,y)与高斯核函数G(x,y,σ)的卷积

L(x,y,σ)=G(x,y,σ)⊗I(x,y),

(1)

式中： ⊗表示卷积运算，σ为尺度空间因子. 高斯核函数的定义表达式为

(2)

为了使得到的特征点更有效， 可以采用差分高斯金字塔DoG， 它是通过高斯金字塔中相邻尺度空间函数相减得到， 即

D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))×

I(x,y)=L(x,y,kσ)-L(x,y,σ).

(3)

1.1.2 关键点定位

利用DoG函数的二阶泰勒展开式对局部极值进行拟合， 从而精确定位出特征点的位置与尺度， DoG的泰勒展开式为

(4)

1.1.3 关键点主方向计算

为了保证图像的旋转不变性， 需要为每个特征点指定一个方向. 特征点邻域像素梯度模值和方向计算表达式如下

(5)

式中：L为特征点的尺度， (x,y)表示特征点像素的具体位置. 将梯度方向直方图的峰值方向定义为该特征点的方向.

1.1.4 关键点描述子构造

以特征点为中心， 把它的邻域范围分成4×4的小区域， 共包含16个种子点， 每个种子点有8个方向的梯度信息， 将最终形成的128维描述子称为SIFT描述子.

1.2 特征点匹配

在待匹配图像中查找与参考图像每个特征点最近邻的两个特征点， 如果最近的距离除以次近的距离小于某个固定的阈值， 则选取最近距离的这一对匹配点作为匹配对.

2 改进的SIFT算法

传统的SIFT算法构造了128维特征描述子， 这在特征点匹配阶段采用欧氏距离计算最近邻和次近邻距离时的计算量很大， 会消耗大量的匹配时间. 本文结合图像的二维熵加快图像的匹配速度.

2.1 算法原理

图像的二维熵能够突出反应利用SIFT算法提取出来的特征点位置的灰度信息与其邻域像素平均灰度的分布关系. 像素点二维熵越大， 则说明该点包含的内容越多， 纹理信息越丰富. 在特征点提取阶段， 关键是要提取出适量而稳定的特征点， 如果特征点数量太多， 在匹配阶段会消耗大量时间， 如果数量太少， 对匹配效果也会产生影响. 根据图像二维熵与SIFT的基本原理， 二者都与图像灰度值有紧密联系， 由此可以通过控制特征点位置二维熵的阈值有效筛选出稳定性高的特征点， 从而为特征点匹配节省时间. 在特征点匹配阶段， 如果参考图像与待匹配图像两个特征点的二维熵差值太大， 则这两点一定不是正确匹配对. 因此利用图像二维熵可以实现对伪特征点的剔除以及正确匹配对的寻找.

为了加快图像的匹配速度， 本文对SIFT算法进行改进. 首先计算利用SIFT算法初步提取出来特征点位置的二维熵大小， 其中图像的二维熵定义如下

(6)

式中： (i,j)表示图像中的某一个像素点的灰度值与其邻域像素点平均灰度值组成的特征二元组， 其中i为某点像素的灰度值，j为其邻域像素灰度的均值，f(i,j)为二元组(i,j)出现的次数，N为图像的尺度.

通过分析SIFT算法寻找特征点与图像二维熵的原理， 可知二者均与图像的灰度值有着紧密的联系， SIFT算法在提取特征点过程中比较同尺度及相邻尺度邻域内的灰度值， 而二维熵值的计算是统计某点及其邻域点像素平均灰度值出现的概率， 二者既紧密相连， 又有所不同， 所以将经过SIFT算法提取出来的特征点再用二维熵进行筛选会使得特征点更加稳定.

如图 1 所示， 白色圆圈表示1个SIFT特征点， 通过计算该特征点与周围5×5邻域像素点的灰度值， 发现灰度变化较小， 二维熵值为3.72. 图 2 所示白色圆圈也是1个SIFT特征点， 此特征点位于雪地与公路的交界处， 计算该特征点5×5邻域像素点的灰度值， 发现灰度值变化较大， 二维熵值为5.34. 由此可见， 某一特征点的二维熵越大， 特征点与邻域像素灰度值相差越大， 即携带的信息越丰富， 特征点更稳定.

图 1 二维熵较大SIFT特征点图Fig.1 Two dimensional entropy larger SIFT feature point map

图 2 二维熵较小SIFT特征点图Fig.2 Two dimensional entropy smaller SIFT feature point map

通过统计图像特征点个数与二维熵值大小关系， 得到图 3 所示示意图， 由图像可知， 当二维熵取值在[4,6]之间时特征点个数变化缓慢， 即此时特征点最稳定.

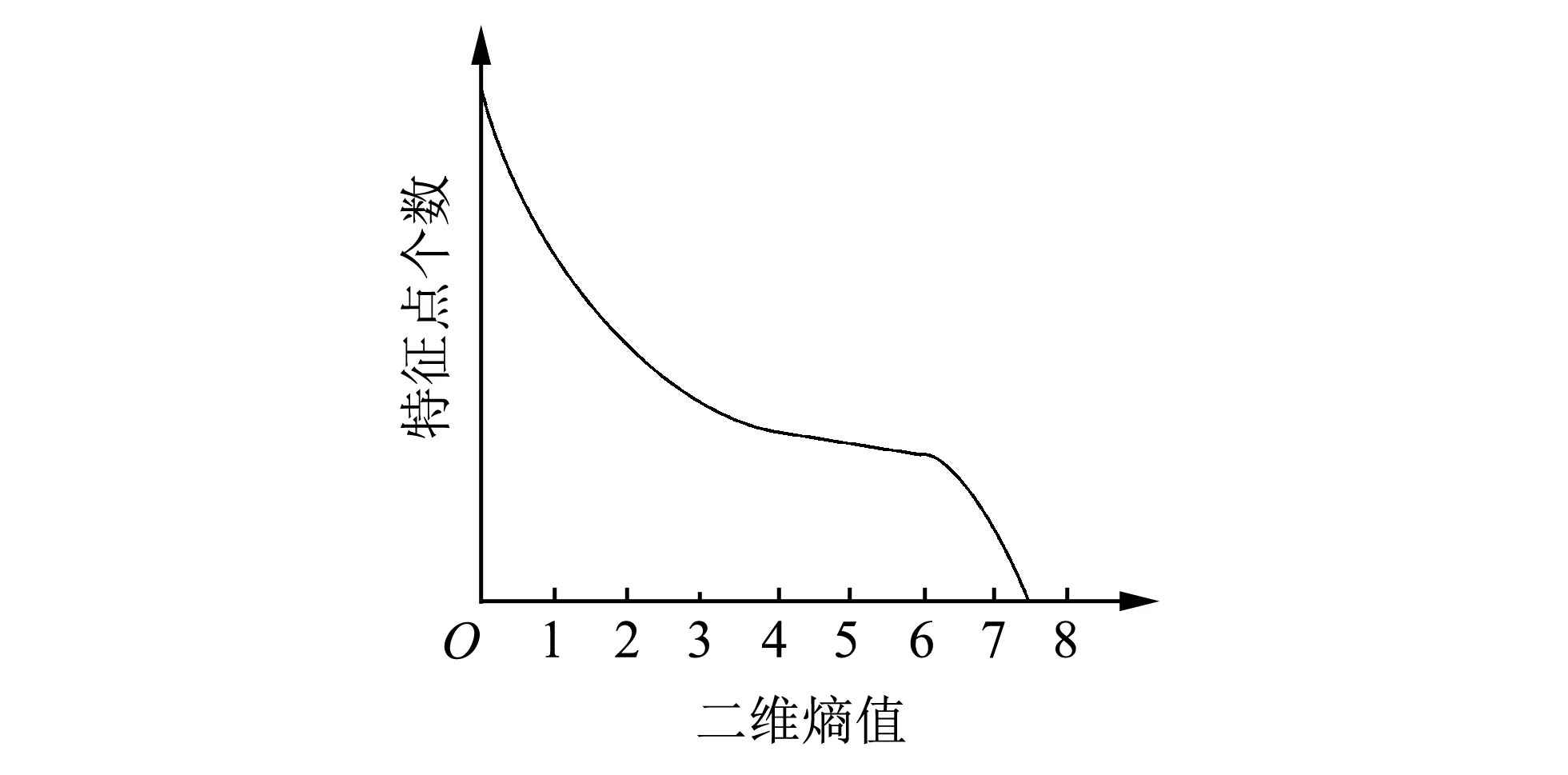
图 3 二维熵与SIFT特征点关系图Fig.3 Two dimensional entropy and SIFT characteristic point diagram

由图 3 可知选取合适的二维熵值对剔除不稳

定的特征点有重要意义. 如图 4 所示， 根据二维熵的定义分别计算参考图像与待匹配图像特征点位置二维熵的大小Q， 判断其与阈值T1和T2的相对大小， 若T1≤Q≤T2， 则保留， 否则为不稳定的特征点需要剔除. 通过遍历计算图像各像素点二维熵值大小， 得出大部分特征点二维熵取值在4～6 之间， 若取值小于4则难以剔除不稳定特征点， 若大于6则得到特征点个数渐趋于0， 故本文取T1=4，T2=6， 可以有效剔除不稳定特征点. 经过此步， 可以剔除一部分不稳定的特征点， 由于提取出来的特征点数量减少， 所以必定会为特征点的匹配节省大量时间.

图 4 特征点筛选图Fig.4 Feature point screening diagram

在特征点匹配阶段， 位于两幅图像重叠区域中的同一特征点在参考图像与待匹配图像中的二维熵大小应该相同， 但由于两幅图像可能是来自不同时间、 不同光照条件下拍摄得到， 二维熵值会有一定差异， 如果二者相差太大， 则一定不是匹配对. 如图 5 所示， 在特征点匹配阶段首先取参考图像的特征点pt_A1， 计算其与待匹配图像某个特征点pt_B1的二维熵之差， 通过计算参考图像与待匹配图像对应匹配对二维熵之差， 得到差值在0.3左右， 若取阈值大于0.3会使初次得到的匹配点对数量增多， 加大欧氏距离计算量. 如果二维熵之差大于阈值T3(本文取0.3)， 则认为pt_B1一定不是pt_A1的的匹配点， 继续在待匹配图像中查找满足条件的所有特征点， 将满足条件的点初步定为一对匹配对.

图 5 匹配对筛选图Fig.5 Matching pair filter diagram

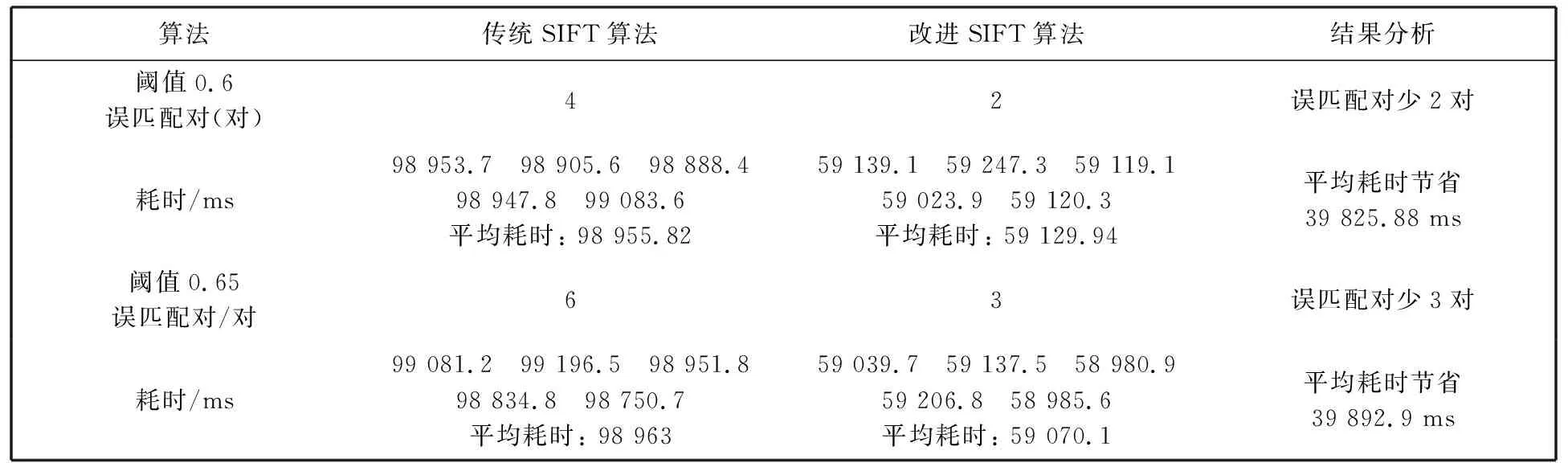
假设待匹配图像中共有m个特征点{Bi|i=1,2,…,m}， 而经过此步找到pt_B3， pt_B8， pt_B10， pt_B12这4个满足条件的特征点， 则在利用距离比法则寻找正确匹配对时只需计算4次128维的欧氏距离， 而传统的SIFT算法则需计算L(4

2.2 算法实现步骤

综上所述， 本文改进的算法实现过程如下：

1) 利用式(6)计算参考图像与待匹配图像中特征点位置的二维熵大小， 剔除不在阈值范围内的点；

2) 计算参考图像与待匹配图像特征点位置二维熵之差， 如果差值太大， 则不是一对匹配对；

3) 利用欧氏距离公式求出参考图像中的特征点在待匹配图像中最近邻和次近邻距离对应的特征点， 如果二者之比小于阈值， 则为一对匹配对.

3 实验结果

为了验证本文算法相对于传统SIFT算法的优越性， 本算法在Intel Corei7-4770 3.40 GHz的CPU， 8GB内存的Windows7操作系统上利用Visual Studio结合OpenCV实现.

3.1 特征点提取实验结果

图 6 为传统SIFT算法提取特征点结果图， 图 7 为改进SIFT算法提取特征点结果图.

对比图 6 和图 7实验结果， 可知改进后的算法特征点数目有所减少. 为了更加直观体现改进算法相对于传统SIFT算法的优越性， 对实验重复进行的5次取其平均值， 实验得到的数据如表 1 所示.

图 7 改进SIFT算法实验结果图Fig.7 Improved SIFT algorithm result diagram

表1 特征点提取两种算法实验数据对比

由表 1 实验数据可知， 改进后的SIFT算法相对于传统SIFT算法特征点数目有所减少， 参考图像中可以剔除掉73个伪特征点， 而待匹配图像中可以剔除掉82个伪特征点. 在特征点提取所用时间上， 可以分别节省600 ms和900 ms左右.

3.2 特征点匹配实验结果

根据传统SIFT特征点匹配原理中提出最近邻点与次近邻点的比例阈值为0.8， 针对本实验， 选最近邻点与次近邻点的比例阈值分别为0.6 和 0.65 进行实验， 太大会使误匹配对增多， 太小使得匹配点对太少直接影响后续图像融合的鲁棒性. 图 8 为传统SIFT算法和改进SIFT算法在阈值为0.6时的匹配结果图， 图 9 为传统SIFT算法和改进SIFT算法在比例阈值为0.65时的匹配结果图.

对比图8与图9可以发现改进的SIFT算法相比传统SIFT算法误匹配对数目减少， 即改进算法具有较强的鲁棒性. 为了验证改进算法在匹配速度上的优势， 在不同比例阈值下， 重复进行5次实验取其平均值， 得到匹配所耗时间并统计误匹配对个数， 实验数据如表 2 所示.

由表 2 数据可知， 当最近邻点与次近邻点的比例阈值为0.6时， 改进算法中误匹配对减少2对， 匹配速度为传统SIFT算法的1.6倍. 而当阈值为0.65时， 误匹配对数目减少3对， 匹配速度为传统SIFT算法的1.6倍. 由此可见， 随着比例阈值的不同， 改进SIFT算法误匹配对数目相对传统SIFT算法都有所减少， 而且匹配速度为传统SIFT算法的1.6倍， 体现了本文改进算法的优越性， 即在保持传统SIFT算法鲁棒性的基础上， 匹配速度有明显的提升.

图 8 阈值为0.6时匹配结果图Fig.8 Matching result graph when the threshold is 0.6

图 9 阈值为0.65时匹配结果图Fig.9 Matching result graph when the threshold is 0.65

表2 特征点匹配两种算法实验数据对比

4 结 论

本文在传统SIFT图像匹配原理基础上， 提出一种结合图像二维熵的SIFT改进算法. 实验结果表明， 改进算法能够有效剔除不稳定的特征点， 同时在特征点的匹配阶段可以节省大量时间. 结合图像二维熵的SIFT匹配算法与传统SIFT算法相比， 具有更好的鲁棒性与优越性.