带对数非线性项的p-Laplacian型方程的多解性

贾文艳， 王淑丽， 郭祖记

(太原理工大学 数学学院， 山西 太原 030024)

0 引 言

p-Laplacian型方程不仅在生物化学以及生物种群动态等许多物理领域中被广泛应用, 而且在几何学等数学领域中也有很重要的理论意义. 因此p-Laplacian型问题的研究受到了许多中外学者的关注, 并取得了很多研究成果[1-5].

文献[6]研究了如下的p-Laplacian型问题

并利用变分法讨论了当λ满足一定条件时, 该问题解的存在性. 考虑如下的p-Laplacian型问题

当λ<0时, 该问题没有非平凡解[7-8]. 当λ>0时, 问题可分为p=2和p≠2两种情况讨论.文献[9-10]讨论了p=2时, 问题非平凡非负解的存在性. 文献[11-13]讨论了p≠2 且λ满足一定条件时, 该问题有一个非平凡解的情况. 然而, 关于带有变号对数非线性项的p-Laplacian型方程没有过多的研究. 受以上工作以及文献[14]的启发, 本文研究以下带有变号对数非线性项的p-Laplacian型方程

式中：Ω为Rn中的光滑有界区域,λ>0, Δpu=div(|u|p-2R. 与文献[15]中带有正非线性项的p-Laplacian型方程相比, 因为f是变号的, 所以本文具有一定的研究价值.

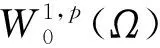
得到的主要结果如下.

(1)

则问题(P)至少有两个非平凡解, 其中|Ω|n为Ω在Rn中的测度, Lp由式(2)定义.

1 预备知识

引理1 (对数Sobolev不等式[16]) 设p>1,μ>0且u∈W1,p(Rn){0}, 则

其中，

(2)

(3)

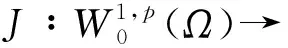
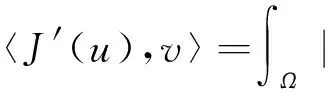
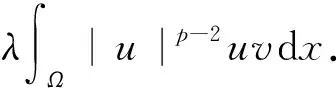
(4)

因此, 问题(P)的解等价于泛函J的临界点. 以下假设式(1)满足.

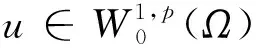
(5)

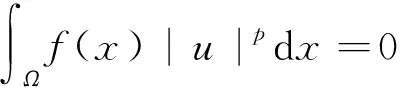
(6)

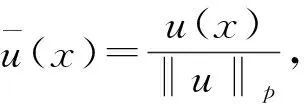
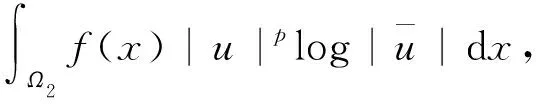
(7)

(8)

由对数Sobolev不等式(3)和式(8)得

(9)

将式(7)～(9)代入式(6)可得

2 解的多重性

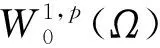
显然,J的非平凡临界点一定在N上.由式(4)可知

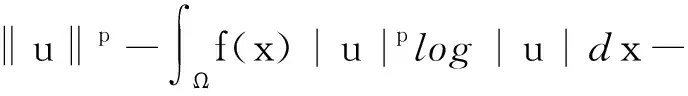
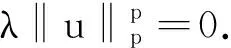
(10)

则

(11)

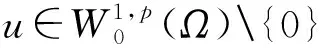
证明由式(10)和式(11)可得

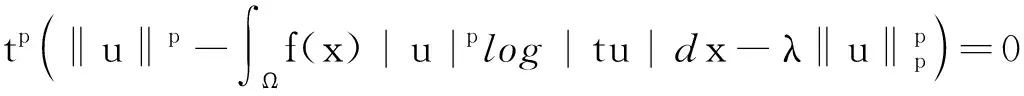
若u∈N, 则

因此我们可将N分为三部分: N+, N-和N0, 其中

引理4 若u0是J在N上的一个局部极小元且u0∉N0, 则J′(u0)=0.

证明设u0是J在N上的一个局部极小元, 则由拉格朗日乘数法知, 存在δ∈R使得

J′(u0)=δφ′(u0),

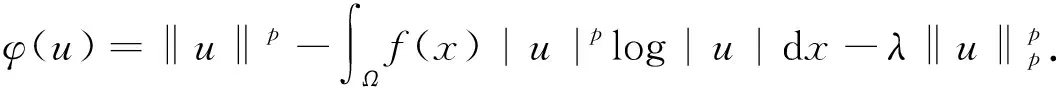
0=〈J′(u0),u0〉=δ〈φ′(u0),u0〉.

另一方面, 由于u0∉N0, 因此

故δ=0, 进而J′(u0)=0.

引理5 N+, N-均非空.

证明由式(11)知,gu有唯一驻点

因此, N+, N-均非空.

引理6 N+是有界的.

vn→v0在空间Lp(Ω)中.

又由un∈N和式(10)知

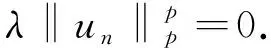
(12)

直接计算可得

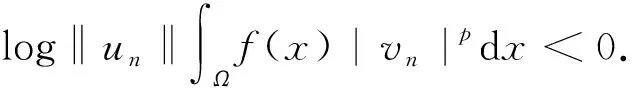
(13)

类似式(7)～(9), 应用‖vn‖=1知

(14)

其中C与n无关. 再由式(13)～(14)及‖un‖→∞(n→∞)可得

(15)

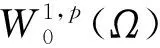
J(v0)≥

(16)

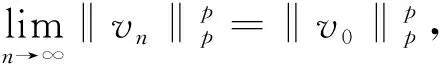
(17)

(18)

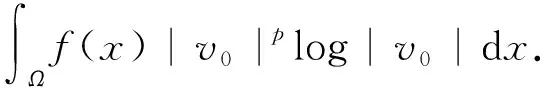
(19)

再结合式(13)和式(15)有

矛盾!

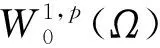
另一方面, 由vn→v0知, 存在{vn}的子列, 仍记作{vn}, 使得式(17)和式(19)成立, 且有

(20)

再结合式(13)和式(15)有

矛盾! 因此, N+是有界的.

引理7 1)J在N+上下方有界;

2)J在N+上有极小元.

证明1) 因为u∈N+, 所以由式(10)可得

由引理6知, N+是有界的, 故J在N+上下方有界.

un→u0在空间Lp(Ω)中.

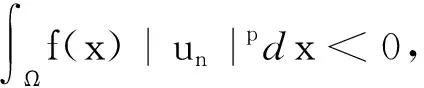
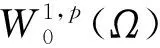
(21)

(22)

(23)

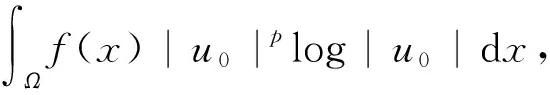
(24)

成立, 再结合式(12)有

因此, 存在

使得t(u0)u0∈N+, 则gu0在t(u0)处取得极小值, 再结合式(21)～(24)有

即u0是J在N+上的极小元.

引理8J在N-上的每一个极小化序列都是有界的.

证明设{un}是J在N-上的一个极小化序列, 即

vn→v0在空间Lp(Ω)中.

由un∈N知, 式(12)成立. 直接计算可得式(13) 和

(25)

结合式(25)及‖un‖→∞(n→∞)可得式(15).

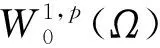
矛盾!

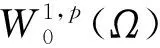
另一方面, 由vn→v0知, 存在{vn}的子列, 仍记作{vn}, 使得式(17)～(20)成立, 再结合式(15)和式(25)有

矛盾! 因此,J在N-上的每一个极小化序列都有界.

vn→v0在空间Lp(Ω) 中.

因为un∈N-, 所以

由un∈N知, 式(13)成立. 直接计算可得式(13) 和式(14). 再由‖un‖→0(n→∞)可得式(15).

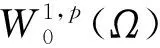
矛盾!

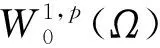
再由式(15)和引理2得

另一方面, 由vn→v0知, 存在{vn}的子列, 仍记作{vn}, 使得式(17)～(20)成立, 再结合式(13)和式(15)有

2)J在N-上存在极小元.

n→∞.

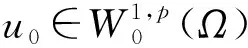
un→u0在空间Lp(Ω) 中.

因此

(26)

由un∈N知, 式(12)成立.

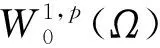
矛盾!

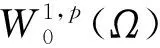
另一方面, 由un→u0知, 存在{un}的子列, 仍记作{un}, 使得式(22)～(24)成立, 且有

再结合式(12)和式(26)有

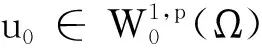
un→u0在空间Lp(Ω) 中.

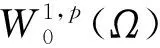
则存在

因此

又由于映射gun(t)在t=1取得极大值. 因此

故

定理1证明由引理7(2), 引理9(2)表明泛函J有两个极小元u+∈N+和u-∈N-. 再由引理4知,u+和u-是问题(P)的两个非平凡解.