基于格子Boltzmann方法的液压激振管道压力冲击的研究
2019-02-22吴万荣郝前华
袁 鑫, 吴万荣, 郝前华,2
(1.中南大学 机电工程学院,长沙 410083; 2.湖南人文科技学院 能源与机电工程学院,湖南 娄底 417000)
液压激振系统中,由于泵的启停或阀的快速换向使液压油的流速发生急剧变化,在管道中会产生强烈的液压冲击[1]。不仅会对管道及相应设备造成破坏,还会造成振动能量的损失,影响激振系统的性能[2]。因此,如何有效利用管道中的瞬变冲击能量,对提高液压振动系统的激振性能有着重大意义[3]。文献[4]通过对这种瞬变的压力冲击的研究,巧妙地加以利用,使原本有害的液压冲击变为有利的激振能量。
对于管道液压冲击的研究,最常用的就是经典水击模型。关于水击的研究,传统的数值方法着眼于宏观物质,在宏观层面上,流体被假设为连续介质。流体运动满足质量守恒、动量守恒以及能量守恒(Navier-Stokes方程),然后求解宏观的N-S方程。目前,水击的计算方法通常采用特征线法(MOC),有限体积法等[5]。
20世纪90年代初,格子-玻尔兹曼方法(LBM)迅速发展,为水击现象的研究提供了一种新方法。与基于宏观连续方程的传统方法不同,LBM着眼于介观粒子,在介观层面,假设流体由离散粒子系统组成,单个粒子在统计学上反映了流体分子热运动的特征。 只要对粒子系统建立合理的演化机制,便能通过统计物理方法得到符合实际物理规律的宏观流动运动特征[6]。因此,LBM是一种完全不同于传统方法的数值模拟方法。
与传统数值方法相比,LBM方法简单,几何边界条件易于处理,易于编程实现,并具有完全并行性,可大大提高计算效率。另外,因为LBM是基于介观粒子的运动分布,故理论上能够从更深层次上描述物质,能更精确地模拟物质的真实状态。LBM自从问世以来,逐渐被应用于物理、化学、医学等多种学科的不同领域[7],并都得到了令人满意的效果。近几十年来各界学者们纷纷开始进行研究,LBM作为一个新兴的交叉学科,正处于不断发展中。文献[8-10]分别采用单松弛LBM和多松弛LBM对给水管路进行模拟,并与传统MOC结果进行对比,验证了LBM的可行性与适用性。本文采用LBM对液压激振系统中管道的液压冲击现象进行模拟,并与CFX方法[11]的模拟结果进行对比,验证并讨论了该方法在这类问题研究上的可行性与优越性,同时也为液压激振系统的进一步研究提供了新的思路。
1 液压激振系统及传统分析方法
1.1 液压激振系统
为合理有效地利用液压冲击能量,搭建了液压激振系统,如图1所示。该系统结构简单,利用管道末端开关阀的开闭来产生液压冲击,从而驱动液压缸输出激振力。
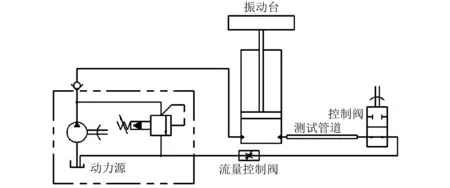
图1 液压激振系统Fig.1 Hydraulic excitation system
1.2 激振系统流体的周期性压力波动机制
由图1可知,在测试管道中,由于阀门的急剧关闭或开启使液体的流速发生急剧变化,从而引起液体压力骤然大幅波动,这种由速度的突变引起的液压冲击波动机制[12],如图2所示。
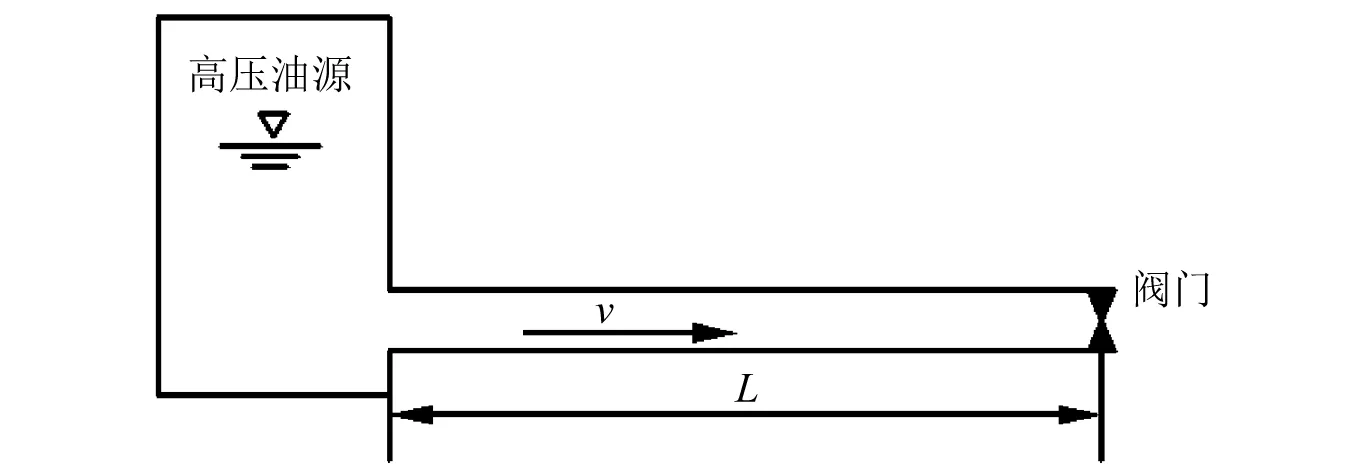
图2 管道压力波动机制Fig.2 Mechanism of pipe pressure fluctuation
实际中,阀门的关闭总是需要一定的时间,如果把整个关闭过程分解成n个微小的瞬时关闭过程,则每个瞬时都会产生一个冲击波,管道内压力的变化都是n个瞬时冲击波叠加的综合结果[13]。
1.3 压力冲击研究的传统方法
研究压力冲击(或水击)规律,传统的方法是基于宏观连续性方程、运动方程。
根据质量守恒,可得管道流体的连续方程
(1)
根据动量守恒,可得运动方程
(2)
式中:p为压力;c为流体中波速;α为管轴与水平面的夹角;u为流速;g为重力加速度;λ为阻力系数;D为管道内径;x为位置坐标,其正方向指向阀门;t为时间。
运动方程和连续方程构成了流体管路瞬变分析的基本方程组,又称为波动方程[14]。波动方程是流体管路瞬变分析的理论基础。当前,各类流体管路的瞬变分析数学模型均以此为基础进行推导。液压冲击的特征线模型通过特征线法求解微分方程[15],沿其特征线将偏微分波动方程变换成常微分方程,然后再进行积分,即可得到便于数值处理的有限差分方程。然后可通过编程进行数值求解[16]。
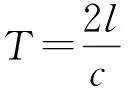
2 格子-玻尔兹曼方法(LBM)
从物理学角度看,流体是由大量分子构成的一个离散系统,构成流体的分子数量巨大,每个分子都作无规则运动。不关心单个分子的运动情况,将若干分子看成一个粒子,则流体可看作是若干离散粒子组成的。通过对大量离散粒子的统计分析就可得到流体运动的宏观特性。LBM正是基于这一理论,把时间和空间完全离散,将流体离散为若干粒子,将流场划分为网格,让这些粒子的分布函数沿网格线运动,并在网格点上根据一定的规则相互碰撞。分布函数的演化在宏观上反映了流体的运动规律,流场的密度、速度、压力等力学参数都可由分布函数的计算得到。目前通常采用的LBM模型有:D1Q3, D2Q9, D2Q7, D2Q13, D3Q15, D3Q18, D3Q27等(D为维数,Q为粒子运动方向的总数)。LBM常用的格子模型示意图,如图3所示。
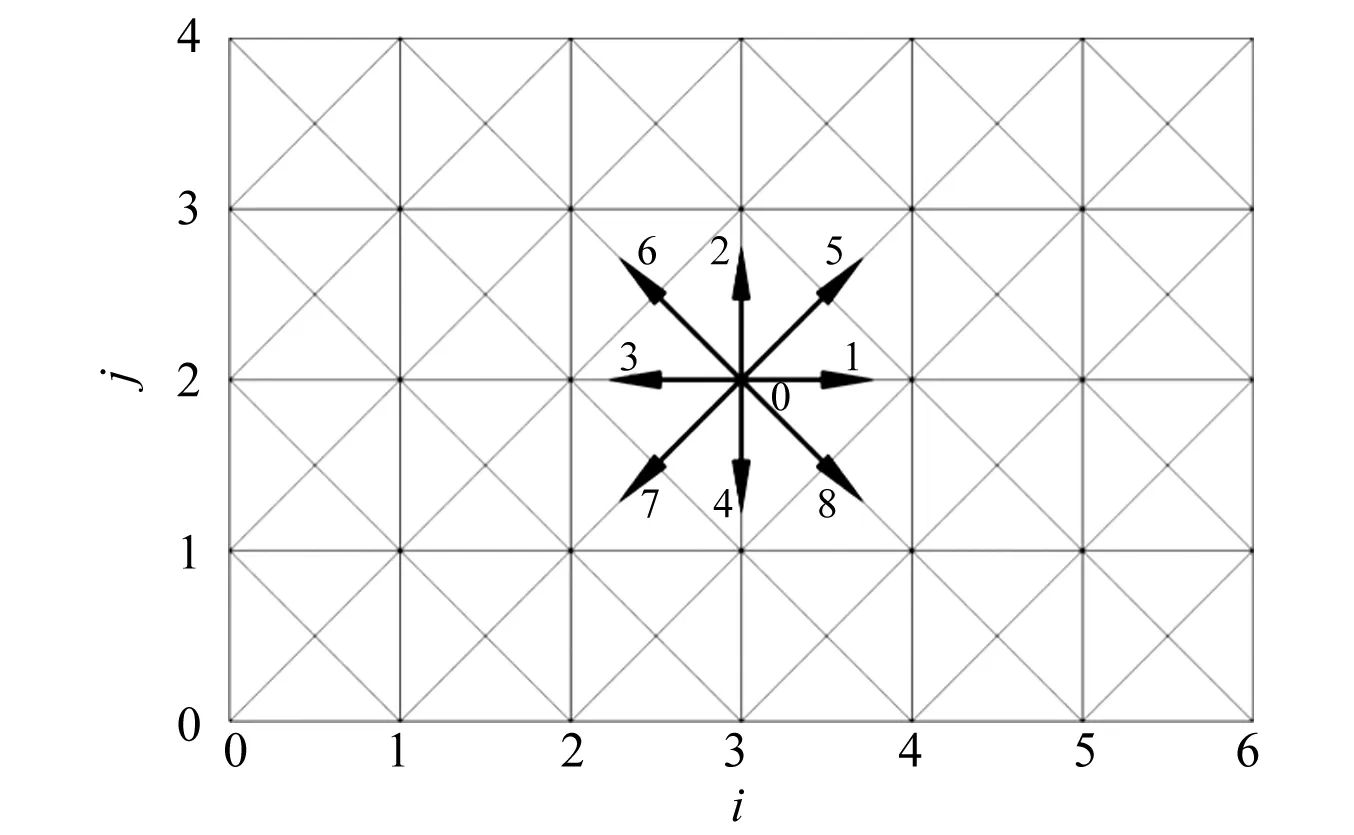
图3 格子模型示意图Fig.3 Schematic diagram of lattice model
2.1 多松弛格子Boltzmann方法
程永光等和李彦浩等用单松弛格子Bltzmann方法(SRT-LBM)分别模拟了一维和二维水电站水击,得到了与特征线法吻合较好的结果,证明了该方法的可行性。但SRT-LBM只有一个可调的松弛因子,因此其稳定性较差,黏性较小时容易失稳。随着多松弛格子玻尔兹曼方法(MRT-LBM)的提出,其优点是能提高稳定性和精度,MRT-LBM建立了与速度空间相对应的动量空间[17],不同动量空间表征特定的物理量,并且采用不同的松弛时间,因此,在物理原理和参数选择上较单松弛格子玻尔兹曼方法(SRT-LBM)具有更大的优势。李彦浩等采用MRT-LBM对水电站水击进行了模拟,验证了其稳定性。将在其它领域已得到验证的MRT-LBM方法[18]引入到液压冲击的分析中,以验证这一方法在液压激振领域的适用性及其数值精度。
2.2 D2Q9速度模型
文献[19-20]用LBM分别模拟分析了二维和三维黏性波,发现二维波和三维波都与现有的有限体积法模拟处于同一精度上。因此,为减少模拟时间,并且根据模型的对称性,选择二维模型进行模拟分析。
对于水击问题,常用的二维模型为D2Q9模型,如图3所示。将流场划分为均匀网格,将流体假设成许多只计质量不计体积的微小粒子组成,在同一时刻同一网格节点上,粒子向9个方向运动(见图4),移动到最近的网格节点。其中每个节点上允许一个静止粒子存在,加上与其相邻的有8个节点,所以称为二维九速度格子模型。其演化过程主要分两个步骤:①迁移,粒子从一个节点在一个时间步长内,以恒定的速度运动到相邻节点;②碰撞,在一个节点上从相邻节点运动来的粒子发生碰撞,根据质量、动量和能量守恒规则改变粒子的速度,然后各个粒子又以改变后的速度迁移。这两个步骤交替循环,直到流场达到收敛。
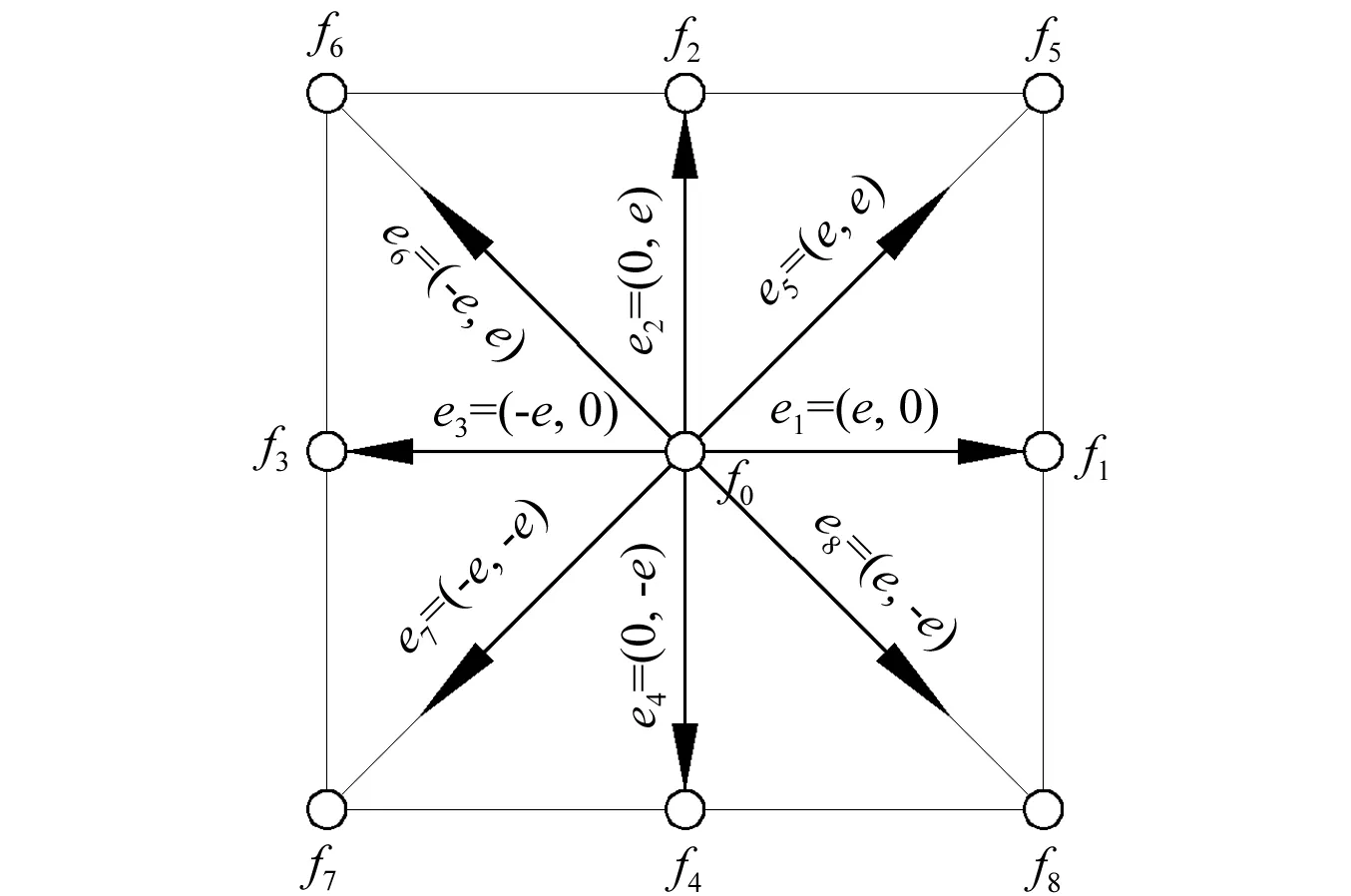
图4 D2Q9速度模型Fig.4 D2Q9 speed model
由图4可知,D2Q9模型在二维平面上共有9种速度
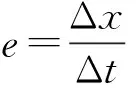
这9种速度的权重因子ω分别为
2.3 液压激振压力冲击的MRT-LBM模型
为了建立能模拟液压激振系统管道压力冲击的MRT-LBM模型[21],必须选择合适的平衡态分布函数来保证与宏观波动方程相容。
2.3.1 演化方程及平衡分布函数
使用多松弛因子的模型的演化方程为
fi(x+eiΔt,t+Δt)-fi(x,t)=-(M-1SM)ij[fj(x,t)-
(3)
式中:fi为粒子分布函数;feq为平衡态分布函数;M为将速度空间映射到动量空间的矩阵;S为表征各个动量空间松弛时间的对角矩阵[22]。
D2Q9模型的矩阵M为

M的逆矩阵M-1为
因为在速度空间中,碰撞步骤难以实现,但在动量空间中,碰撞过程较易实现。将速度空间经线性变换映射到动量空间中来描述碰撞过程,而迁移过程仍在速度空间进行。因此,将碰撞和迁移过程分开描述如下:
碰撞过程
mp(x,t)-m(x,t)=-S[m(x,t)-meq(x,t)]
(4)
迁移过程
(5)
计算宏观量
ρ=∑ifi,ρu=∑ieifi
(6)
式中:m(x,t)为动量空间分布函数,可写为m= (ρ,e,,jx,qx,jy,qy,pxx,pxy)T;meq(x,t)为动量空间的局部平衡态分布函数;fp(x,t),mp(x,t)分别为碰撞后速度空间和动量空间的分布函数。对于D2Q9模型,松弛矩阵S=diag(0,se,sε,0,sq,0,sq,sv,sv)。这样可以更为直观地描述程序实现过程[23]。
对于液压管道压力冲击问题,D2Q9模型的平衡态分布函数为
meq(x,t)=ρ(1,-2+3u2,1-3u2,ux,-ux,uy,-uy,
(7)
2.3.2 Chapman-Enskog展开
与SRT-LBM宏观方程的推导类似,MRT-LBM仍然采用Champan-Enskog展开法进行推导,最终得到 MRT-LBM对应的宏观方程
(8)
(9)
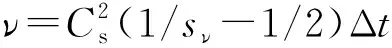
3 激振系统管道液压冲击的MRT-LBM模拟
3.1 物理模型及初始条件
3.2 数值计算模型
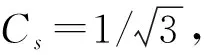
3.3 模拟流程
根据所搭建的数值分析模型,编写以MRT-LBM为基础计算方法的计算机程序对该模型进行模拟仿真。程序的运行流程,如图5所示。
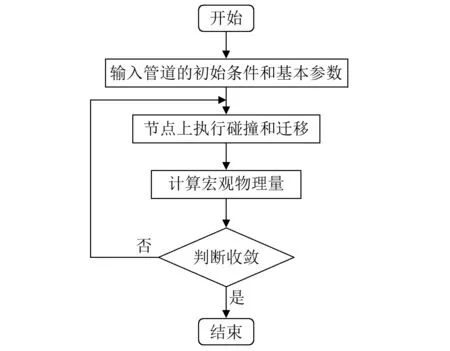
图5 程序运行流程图Fig.5 Flow chart of program operation
4 模拟结果分析
4.1 与CFX方法的对比
将MRT-LBM模拟管道压力冲击现象时得到的结果与CFX的结果进行对比,来进验证MRT-LBM的可行性与准确性。
当ΔT≤T时,即产生直接压力冲击。模拟了关闭时间为0.002 5 s时阀门端压力变化,如图6所示。
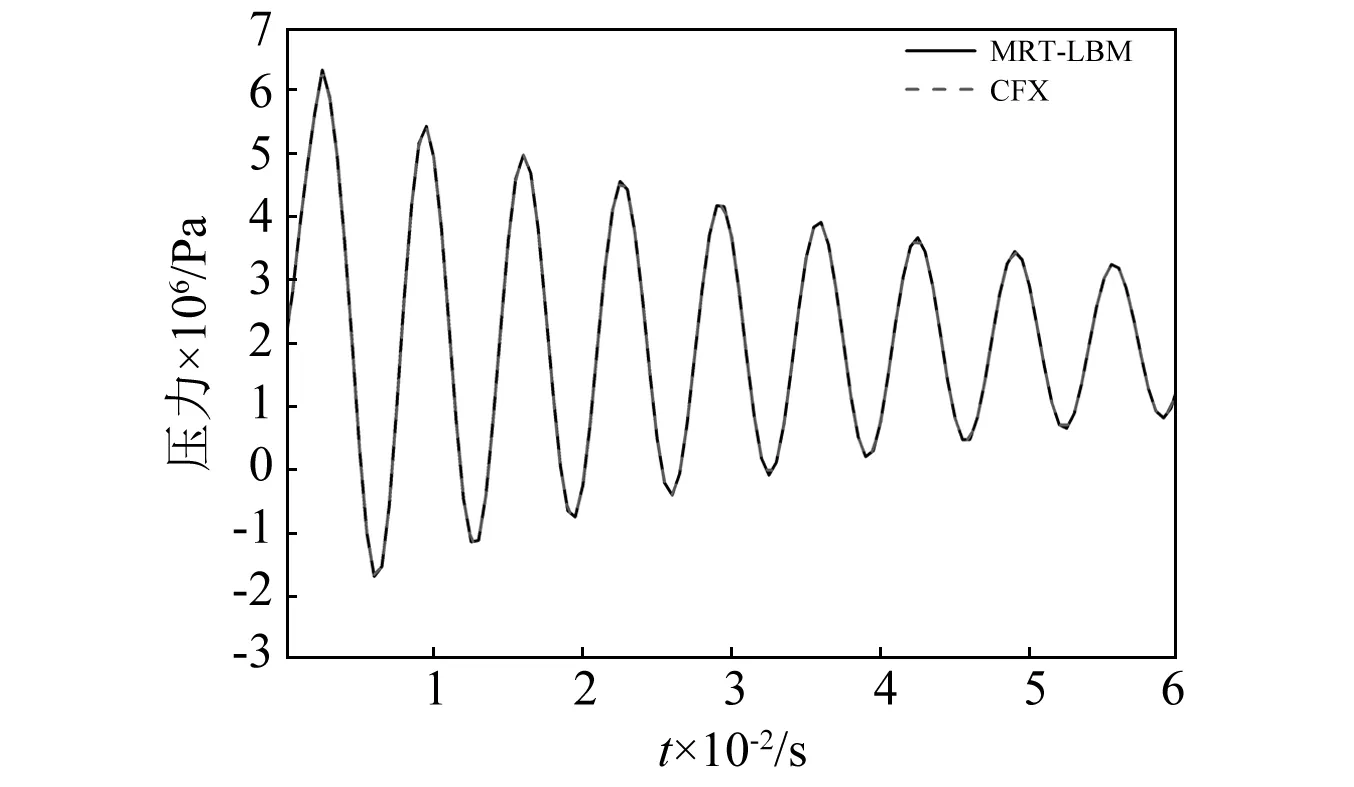
图6 关阀时间为0.002 5 s时阀门端压力变化Fig.6 Pressure variation at the valve end when the closing time is 0.002 5 s
当关阀时间ΔT>T,将产生间接压力冲击。图7~图9分别模拟了在流速线性变化时,关阀时间分别为0.004 s,0.006 s和0.008 s时的阀门端压力变化。
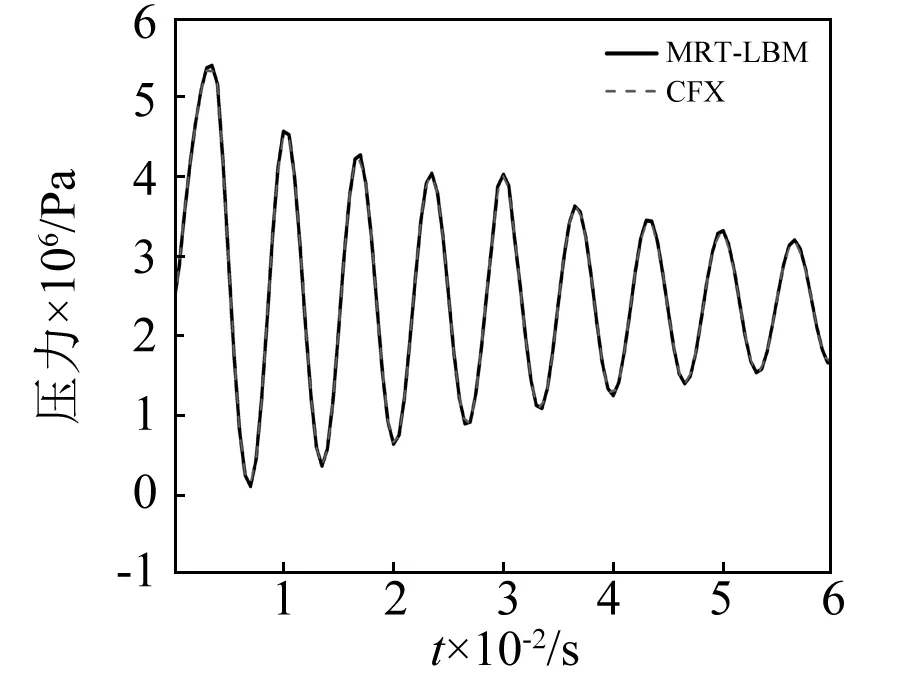
图7 关阀时间为0.004 s时阀门端压力变化Fig.7 Pressure variation at the valve end when the closing time is 0.004 s
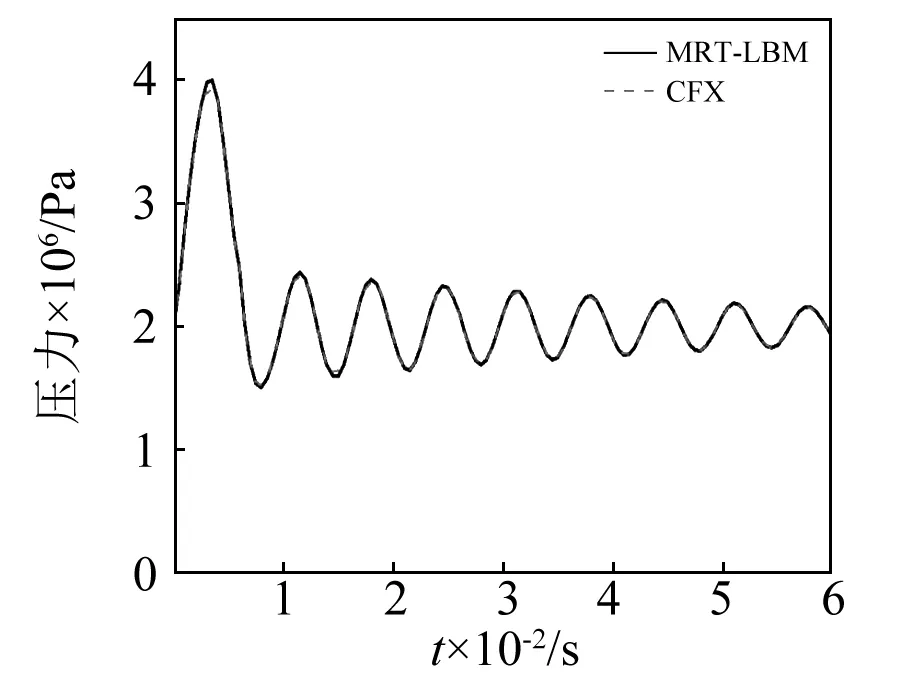
图8 关阀时间为0.006 s时阀门端压力变化Fig.8 Pressure variation at the valve end when the closing time is 0.006 s
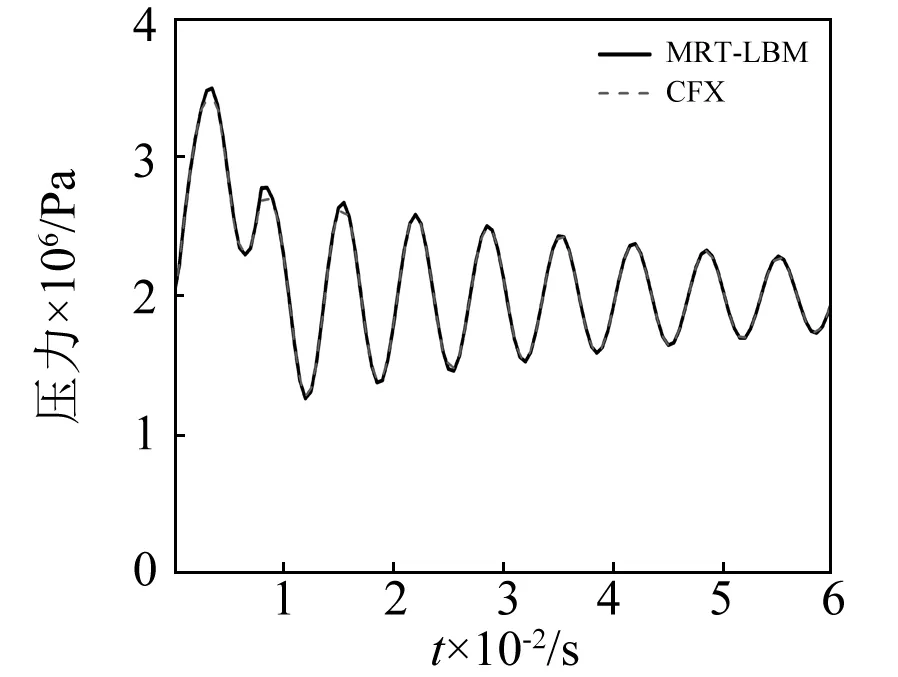
图9 关阀时间为0.008 s时阀门端压力变化Fig.9 Pressure variation at the valve end when the closing time is 0.008 s
MRT-LBM和CFX方法的压力峰值对比,如表1所示,两种方法的仿真时间对比,如表2所示。
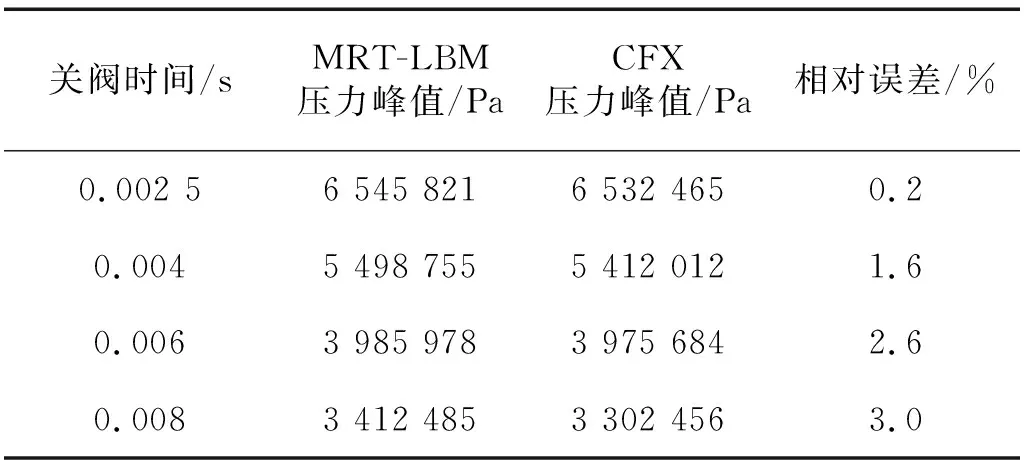
表1 MRT-LBM与CFX的压力冲击峰值对比Tab.1 Comparison of peak pressure between MRT-LBM and CFX
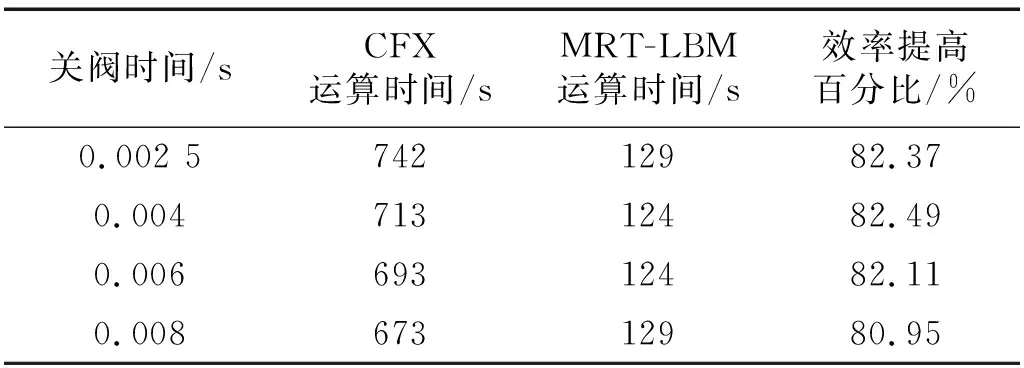
表2 MRT-LBM与CFX仿真时间对比Tab.2 Comparison of simulation time between MRT-LBM and CFX
由图6~图9及表1、表2 可知:
(1)两种模拟方法得到的压力峰值的最大误差为3%,可见文中建立的MRT-LBM模型能较准确地模拟管道内的压力冲击;
(2)直接压力冲击要大于间接压力冲击。主要由于间接压力冲击,在阀门还未完全关闭时,返回的膨胀波已经到达阀门端,就会与阀门端产生的压缩波进行叠加从而削弱了压缩波的效应,减小了峰值压力;而对于直接压力冲击,当阀门完全关闭时,从管道入口端返回的膨胀波还未返回阀门端,因此不会对阀门端产生的压缩波产生叠加而削弱压缩波;
(3)发生间接压力冲击时,关阀时间越短引起的压力冲击越大,且间接水击会在阀门端产生高低压的叠加,不同关阀时间叠加情况也不同,因此会产生如图7~图9所示不同情况的压力冲击;
(4)直接和间接压力冲击的峰值压力与经典的压力变化计算公式Δp=ρcΔν/λ相吻合,式中λ是关阀时间ΔT与水击相T的比值;T也与理论值相匹配;
(5) MRT-LBM在仿真运算时间明显低于CFX方法,运算效率提高>80%。
4.2 管道中流体压力波的传播过程
由图10、图11可知,管道中点处的压力变化相对于阀门端有延迟。压力在管道中以弹性波的形式传播,因此,压力波从阀门端或管道入口处传播到管道中点处都需要一定时间,故有延迟。由于波速在油液中传播速度很快,故在液压激振系统管道中传播的周期就短,因此可实现较高频率的激振,但由于油液的低压缩性使振幅不能达到很大。
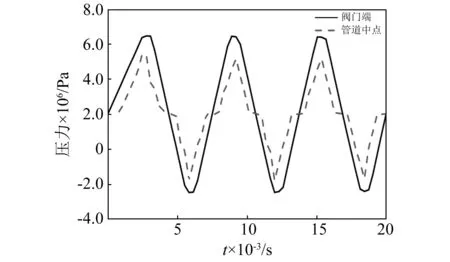
图10 直接压力冲击时管内压力传播Fig.10 Pressure propagation in pipe during direct pressure shock

图11 间接压力冲击时管内压力传播Fig.11 Pressure propagation in pipe during indirect pressure shock
4.3 不同流速变化引起的压力冲击
对于不同的流速变化,会产生不同的压力冲击。通过对阀门处流速的变化进行控制,分析了不同流速变化下压力冲击的变化情况。模拟了两种不同流速变化下引起的不同压力冲击,两种流速变化曲线,如图12所示。
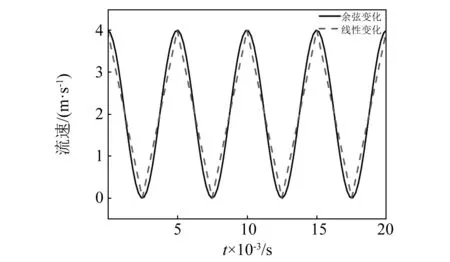
图12 流速变化曲线图Fig.12 Curve of flow velocity changes
由图13可知,压力冲击的变化规律与油液流速变化规律基本一致。当流速线性变化时压力呈线性变化,当流速按余弦变化时压力呈余弦变化。
4.4 管道中流体速度场对压力冲击的影响
根据流体力学的相关知识,流体压力以流体为载体,因此压力的变化是建立在流体流动状态变化的基础上的。因此,借助MRT-LBM的模拟结果对阀门关闭后管内速度场的变化情况进行分析,进一步研究产生瞬变压力冲击的根本原因。
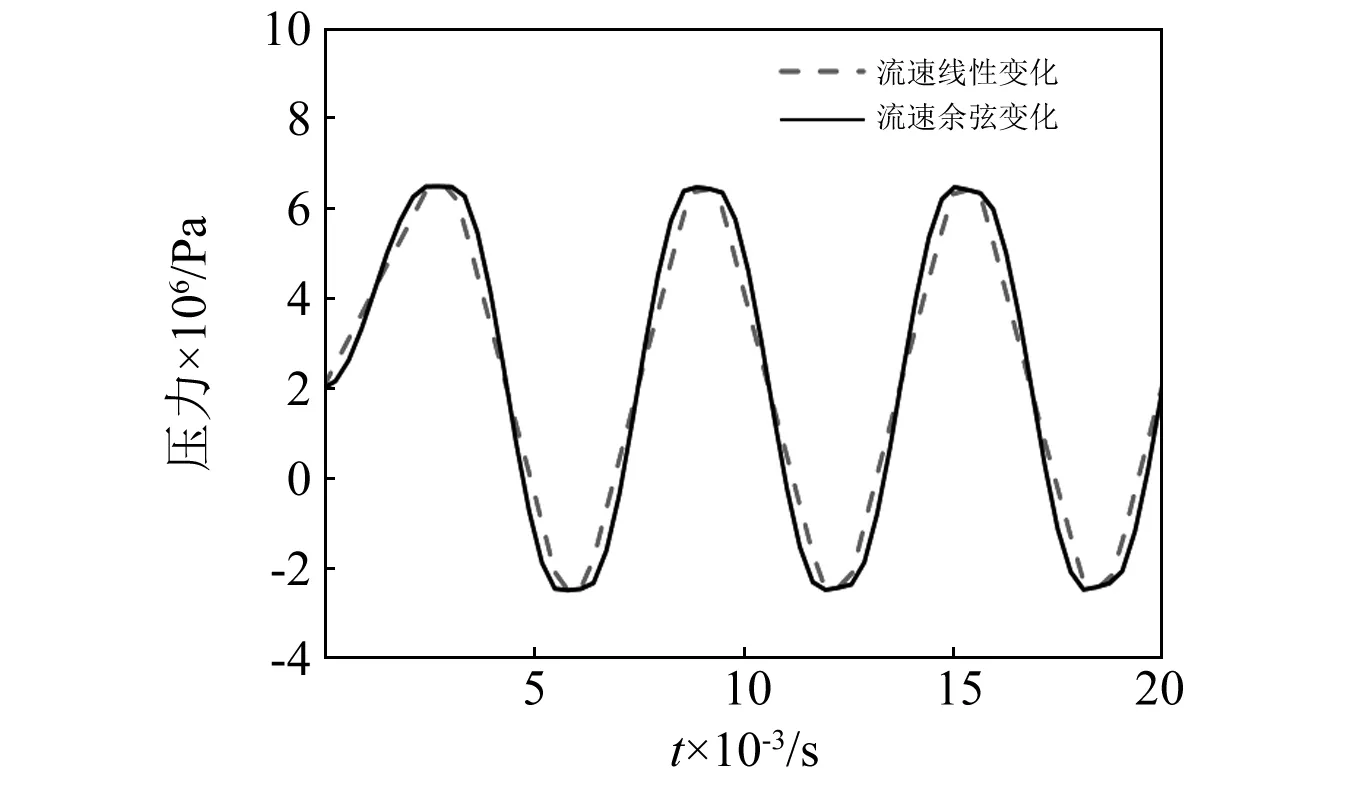
图13 不同流速变化下的压力曲线Fig.13 Pressure curves under different flow velocities
速度场的矢量图能直观地描述阀门关闭后流体的运动变化。由图14中流体的流动规律分析可知,由于黏性流体沿管径方向有速度梯度,当关内流速突变时产生的压力冲击也将有沿管径方向的压力梯度,这个压力梯度又会反过来驱动流体。数值上,阀门端的流速在阀门关闭后迅速降为0,然后在0附近小幅波动。图15直观地描述了管道入口处流体在阀门关闭后的流动变化。相对阀门端,管道入口处的流体运动变化有延迟,故压力冲击也有延迟。数值上,流速在0~3.5波动。可见管内压力冲击产生的根本原因是流体速度的变化,而压力冲击又会反过来影响流速。因此,发生压力冲击时,流速和压力是相互作用的。
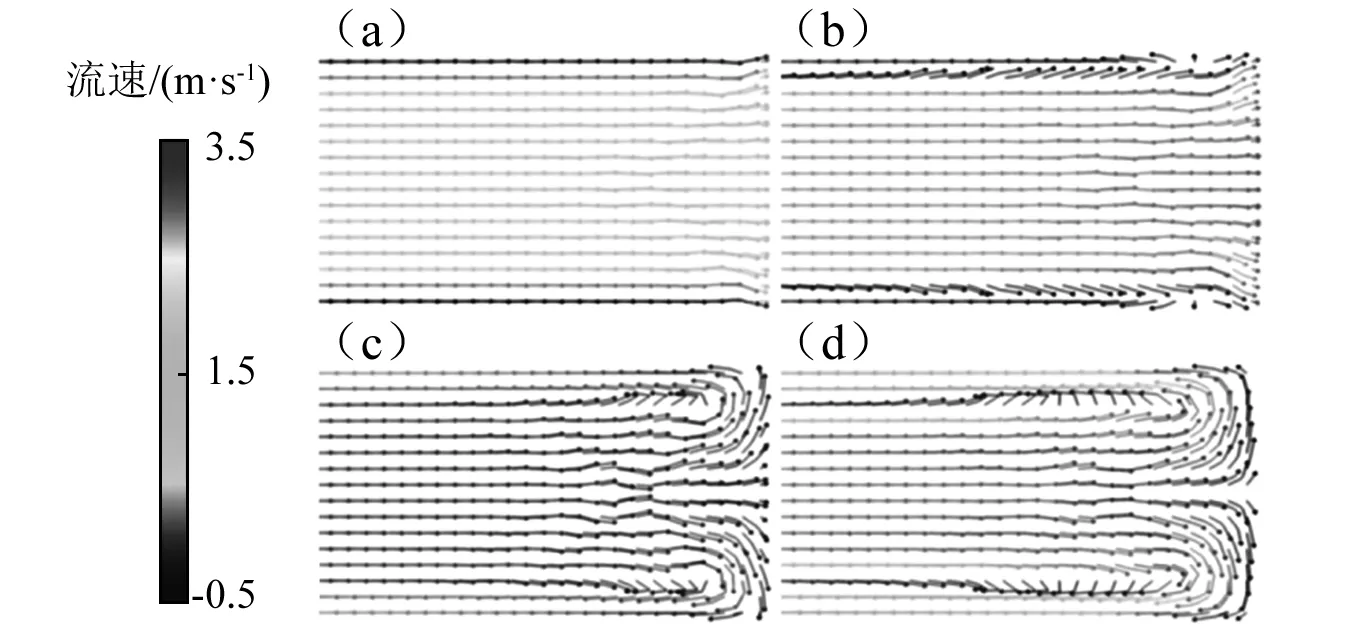
图14 阀门端流体流动变化Fig.14 Fluid flow changes in the valve end

图15 管道入口处流体流动变化Fig.15 Fluid flow changes in the pipe entrance
5 结 论
本文基于介观离散粒子的MRT-LBM对液压激振系统中的压力冲击现象做了初步的模拟分析,验证了该方法在模拟液压激振方面的可行性,并到了合理的结果。同时也为液压激振研究领域提供了新的研究思路。
(1)MRT-LBM具有高稳定性,可用于模拟液压激振系统相关问题,且模拟结果与传统方法有较高的一致性。
(2)关阀水击经过合理控制可用于液压激振。
(3)通过控制阀门的过流来调节液体流速变化,可得到不同情况的压力冲击。
(4)相比CFX方法,MRT-LBM计算效率更高。
(5)运用MRT-LBM的模拟结果,直观地解释了油液速度瞬变是压力瞬变产生的根本原因。
