基于特征参数的栓接结合部螺栓预紧力评估
2019-02-22罗文峰
罗文峰, 余 岭,2
(1. 暨南大学 力学与建筑工程学院,广州 510632; 2. 暨南大学 重大工程灾害与控制教育部重点实验室,广州 510632)
结构连接形式有栓接、铆接、焊接、胶结等,其中栓接结合形式因易于拆卸和承受荷载能力强,而被广泛应用于各类工程结构中[1],如航天器构件拼接、塔吊骨架搭建、管道法兰连接等大都是栓接形式。服役过程中,栓接结合部在冲击、振动和蠕变等荷载作用下,连接强度下降(表现为螺栓预紧力下降),连接件出现滑动、分离甚至松脱现象[2]。结合部损伤降低结构性能和承载能力,轻则影响结构正常运行,重则造成结构失效、破坏,给社会造成巨大损失。为了保证结构的完整性、安全性及功能性,亟需发展监测栓接结合部连接状态的方法。
结合部损伤会改变结构状态,结构动力参数及其时程响应规律会发生变化。Yin等[3]通过不完备的模态振型识别框架结构中的螺栓松动状态。缑白勇等[4]利用固有频率变化定量评估螺栓松动程度较大时的预紧力。实际上,螺栓松动属于局部损伤,频率、振型、低频段传递特性等动力参数主要表征结构整体特性,对结合部的损伤灵敏程度较低。王丹生等[5]基于压电传感器,测量连接节点处的电导纳变化来识别螺栓松动损伤。该方法利用了结构的高频信号,但设备昂贵,测量信号容易受到干扰。杨智春等[6]利用结构加速度时程响应的自相关函数识别螺栓松脱损伤的发生时间及位置,但只考虑了螺栓松脱和紧固两种工况,且需要较多的测点。
螺栓预紧力损失后,结合部连接可能从初始线性状态演化到非线性状态,表现为:切向产生微观上的滑移和宏观上的滑动;法向产生微观上的拍击和宏观上的分离碰撞[7]。Zhou等[8]在有限元模型中添加了连接件分开、螺栓拉裂、材料塑性变形等因素,建立了栓接结合部非线性损伤模型。Zhao等[9]提出用虚拟材料法描述栓接结合部的连接特性。Fasel等[10]基于混沌理论检测结合部损伤状态。这类方法的测试原理和试验设备都很复杂,而不同的连接状态下,栓接结合部带来的非线性响应又具有不同的特点。目前,尚缺乏有效的结合部非线性动力学模型,基于非线性理论的结合部损伤识别还没能应用于工程实际中。
基于线性化理论,在宏观层面上考虑,结合部连接作用可以用弹簧阻尼系统描述,其主要工作体现在特征参数辨识上。Ren等[11]用广义频响函数耦合方法辨识结合部特征参数,将参数辨识转化为一组特征方程的求解,但特征方程条件数很大,在模型误差、测量噪声、数值运算(矩阵求逆)的影响下,辨识结果出现不适定性问题。李玲等[12]先通过求逆运算获得初始值,利用条件数法对试验数据处理后,再进行二次辨识,以提高辨识精度,Tol等[13]则通过优化算法进行二次辨识。求逆运算得到的初始值误差很大,而初始值又决定了二次辨识的参数精度。在利用频响函数法对栓接结合部的研究中,大都是考虑正常工作下的栓接结合部动力特性,而对损伤状态的结合部特征参数变化研究,特别是依据特征参数定量评估螺栓预紧力的文献还很缺乏。
本文在参数辨识方法上,避免矩阵求逆运算,依据特征方程特性,以方程两端加权误差和最小构建目标函数,并通过粒子群优化算法(Particle Swarm Optimization,PSO)获取特征参数,由此提出一种采用正问题求解思路的参数辨识方法。对于实验室栓接结合部结构,进一步讨论了等效线性模型中连接节点自由度数量,对不同预紧力下的辨识参数精度的影响,拟合得到辨识参数与螺栓预紧力之间的关系式,给出预紧力定量评估方法。
1 栓接结合部等效模型
等效线性模型采用弹簧阻尼系统描述结合部作用,并且假设其特征参数不随振动频率和相对位移变化。实际工程中,大多数栓接结合部结构原材料为钢材,忽略阻尼的情况下,可采用弹簧表示栓接结合部的作用。整体结构由子结构和栓接结合部组成,其中栓接结合部等效线性模型,如图1所示。
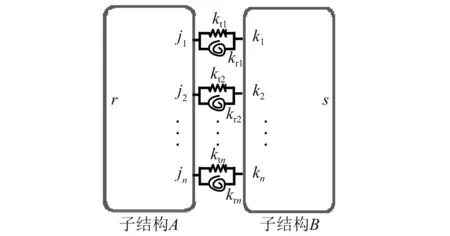
图1 栓接结合部等效线性模型Fig.1 Equivalent linear model of bolted joints
坐标j和k表示子结构连接节点,坐标r和s表示子结构A和子结构B的内部自由度。在频域内,子结构A和子结构B的节点位移与外力的关系为如式(1)和式(2)所示。
(1)
(2)
式中:TT和RR分别为平动和扭转的频响函数;TR和RT为平动与扭转振动相耦合的频响函数;x,θ,f,m分别为平动位移、角位移、力和力矩。
假定结合部连接面内没有外荷载作用,连接节点满足平衡方程及位移协调方程
fj+fk=0;mj+mk=0
(3)
(4)
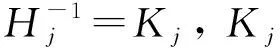
(5)
式中: 上标c为整体结构频响函数。依据式(1)~式(5),可得结合部参数辨识特征方程
(6)
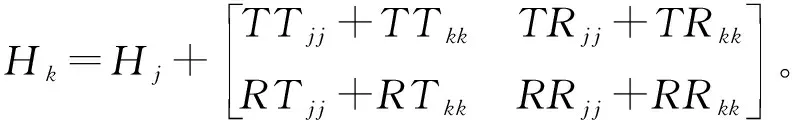
2 参数辨识
2.1 目标函数
从式(6)中4个辨识方程均可表示成通式
Ai(ω)=Bi(ω)×Hk(ω)-1×Ci(ω)
(7)
式中:A为整体结构频响函数与子结构频响函数关系;B,C为子结构频响函数;ω为频率。
采用正问题的思路,避免求逆运算以特征方程两端误差和构建目标函数,通过优化算法,找到使目标函数最小的结合部特征参数。
频响函数在共振点与非共振点间的值存在数量级上的差异,大部分方程的误差水平远小于几个共振点组成方程的误差。为了将方程误差控制在同一水平上,目标函数能准确反映结合部参数与结构性能(频响函数)的关系,本文以方程两端绝对值之和的倒数为权重,使每个方程的误差对目标函数贡献控制在[0, 1]内,构建的目标函数为
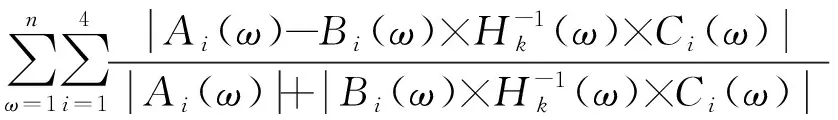
(8)
当求解域内的解等于结合部参数时,辨识方程左右两端相等,目标函数值取全局最小值,为零。实际测量过程中,频响函数不可避免地受到噪声污染,目标函数不可能取零值。想要准确地辨识到结合部参数,目标函数须有良好的鲁棒性,而优化算法须能够搜索到全局最小值。
2.2 粒子群优化算法
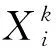
(9)
(10)
式中:Xpb为k个迭代步中粒子的历史最优解;XGb为粒子群的当前全局最优解;c1,c2为权重系数,用以调整飞向自身最优位置和全局最优位置的步长,均设定为2;R()为[0, 1]区间内均匀分布的随机数,使粒子运动具有随机性;w为惯性权重系数,表征粒子保持当前自身速度的能力,w设置为随迭代步线性递减
(11)
式中:wmax取为0.95;wmin取为0.4;CC为当前迭代步数;LC为总迭代步数。
3 数值算例
3.1 数值仿真模型
如图2所示为两根悬臂梁与单个螺栓组成的栓接结合部结构。两根悬臂梁物理参数相同,其中:梁长0.8 m,横截面尺寸0.01×0.05 m2,杨氏模量210 GPa,密度7 800 kg/m3。忽略阻尼和螺栓质量的影响,结合部等效线性模型为一组竖向和扭转弹簧,如图3所示。
利用Matlab软件,采用有限元方法建模。子结构用梁单元建模,等距划分为50个单元,51个节点。弹簧连接节点为N49和N57,内部自由度节点为N13和N90,预设结合部等效平动刚度kt=2×106N/m,等效扭转刚度kr=2×104N·m/rad。取频带范围为0~1 000 Hz,频率分辨率为1 Hz的频响函数为结构响应。实际应用中,测量数据都不可避免地受到噪声的污染,为此将5%和10%的随机噪声添加到频响函数中。

图2 栓接结合部结构Fig.2 Bolted joints structure
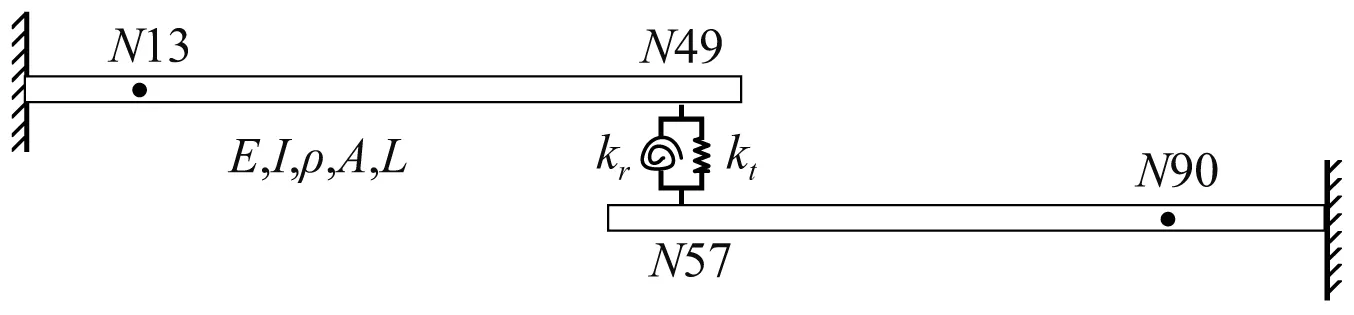
图3 等效线性模型Fig.3 Equivalent linear model
3.2 目标函数性质
数值算例中只含2个未知参数,可在三维坐标下观察目标函数图像。将求解域取为kt∈[1×105,1×107],kr∈[1×103,1×105],等间距地在求解域内取10 000个点,计算其目标函数值,其中无噪声、5%及10%随机噪声的目标函数图像,如图4~图6所示。
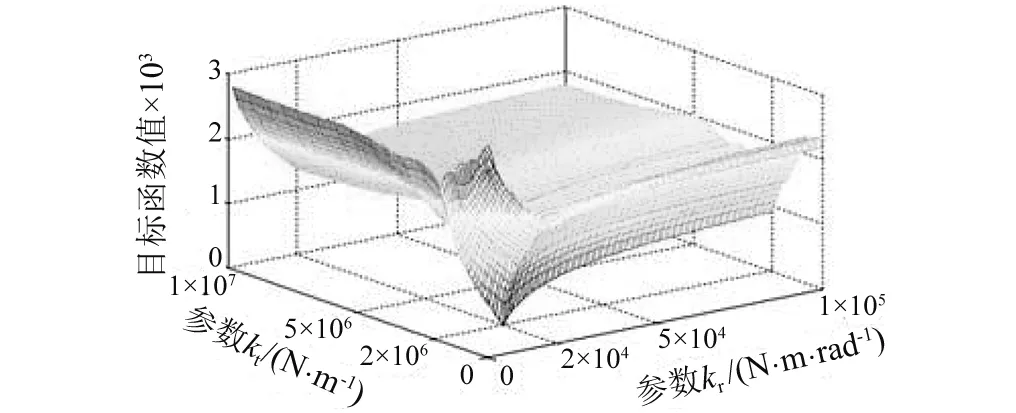
图4 无噪声下目标函数三维图Fig.4 3D graph of J(n,k) under noise-free
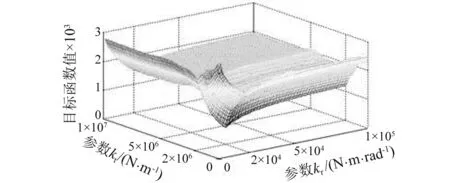
图5 5%噪声下目标函数三维图Fig.5 3D graph of J(n,k) under 5% noise
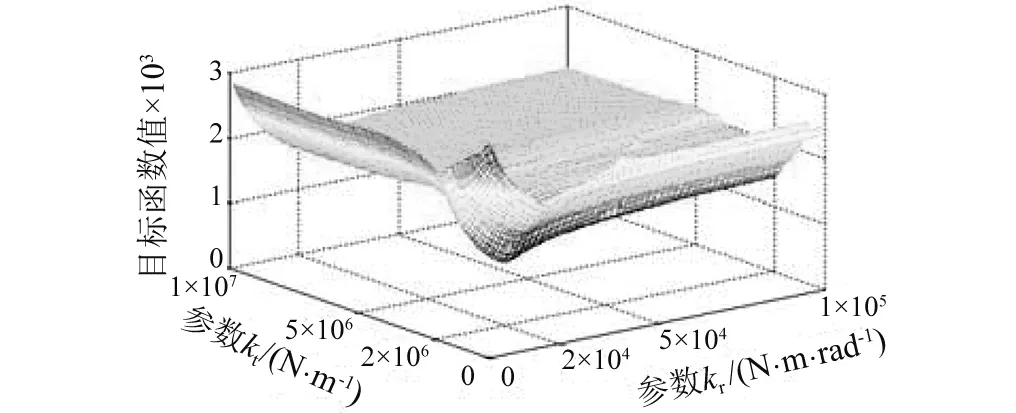
图6 10%噪声下目标函数三维图Fig.6 3D graph of J(n,k) under 10% noise
从图4可知,无噪声情况下,目标函数在结合部参数处取最小值,并在参数附近区域单调递增,当求解域内的点的值很大时,目标函数值保持不变。目标函数具有包含单调区间、光滑、连续等性质,便于优化算法搜索到全局最优解。
噪声污染后的目标函数基本性质不改变,而全局最小值增大:5%噪声水平下,min(J)=610.8; 10%噪声水平下, min(J)=990.7。目标函数虽然受到了噪声的影响,但是最小值依然落在结合部参数附近,说明目标函数具有良好的鲁棒性,本文所提方法有效解决了辨识参数的不适定性问题。
物理意义上,方程右端相当于以求解域内的点为特征参数,得到的整体结构。而方程左端是实测的整体结构频响函数,因此一定区域内,域内的点偏离真实结合部参数越远,连接状态差别越远,体现在频响函数差异越大。目标函数表现为单调递增,说明目标函数能反映参数变化引起的连接状态差异。
连接刚度很大时,螺栓已经拧得足够紧,其动力特性趋于稳定,不再随连接刚度增加而变化,计算的整体结构频响函数不变化,方程误差不发生改变。数学意义上,特征方程式(6)中,结合部参数越大,求逆运算后Hj越小,Hk变化越小,方程右端趋于不变,因此求解域内的点的值很大时,目标函数值保持不变。
3.3 辨识结果
利用PSO算法,对无噪声、5%噪声、10%噪声的目标函数分别迭代求解获取其最小值,种群粒子数为20,迭代30次,求解域kt∈[1×105,1×107],kr∈[1×103,1×105],以一组随机解作为初始种群,算法运行50次,其结果如图7所示。

图7 PSO算法辨识结果Fig.7 Identified results based on PSO algorithm
三种噪声水平下,50次运算结果中,均只有2次未能搜索到全局最小值,表明了PSO算法具有强大的全局搜索能力,适用于求解本问题。噪声水平下,单次运行结果如表1所示,随着噪声水平的增加,误差水平也随之提升,但是其精度依然很高,表明本文所提方法能够精确辨识栓接结合部特征参数。

表1 5%,10%噪声水平下单次辨识结果
4 试验验证
4.1 试验简介
以悬臂梁与自由梁形成的栓接结合部结构为试验对象,验证本文所提的参数辨识方法,并进一步通过辨识参数识别螺栓预紧力。
整体结构试验设备图如图8所示,悬臂梁长度:800 mm,横截面尺寸:50 mm×10 mm;材料为钢材,密度ρ=7 850 kg/m3,弹性模量E=210 GPa;自由梁长度:400 mm,横截面尺寸:50 mm×10 mm;连接件接触范围:50 mm(距悬臂梁固支端750~800 mm)。
通过力锤对子结构自由梁给予脉冲激励,激振器对子结构悬臂梁和整体结构给予正弦扫频激励,采用LMS数据采集仪测量结构频响函数。测得频响函数带宽均为0~2 048 Hz,频率分辨率为1 Hz。

图8 整体结构试验设备图Fig.8 Experimental setup for assembled structure
在整体结构中,内部自由度节点选取为距离悬臂端350 mm,1 050 mm处。结合部等效线性模型用竖向和扭转弹簧模型表示,连接范围内,实验室栓接结合部简图考虑为两个等效模型,如图9所示。一组弹簧模型中,连接节点设在螺栓开孔中心处,即距离悬臂端775 mm处;三组弹簧模型,连接节点设置在765 mm,775 mm,785 mm。
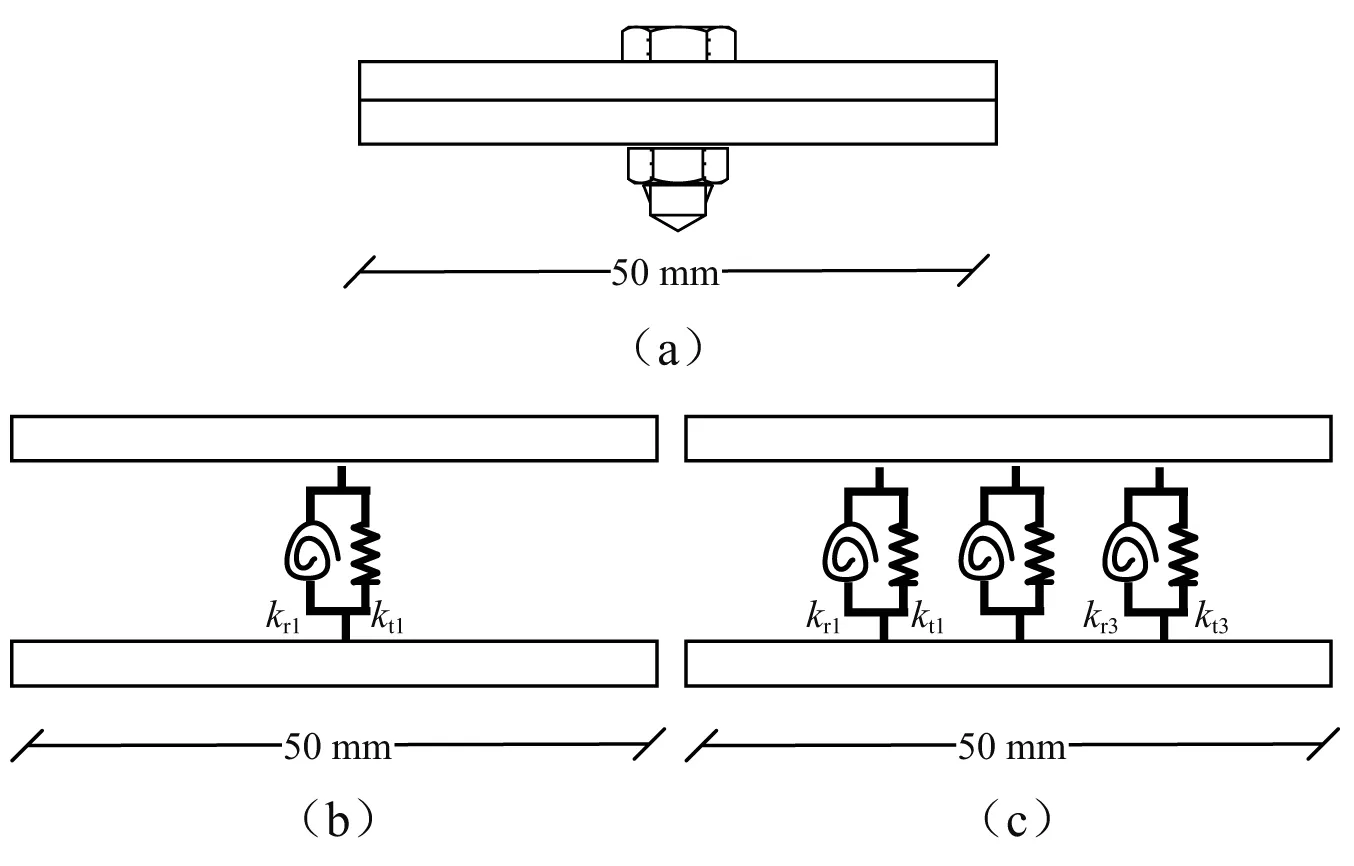
图9 栓接结合部简图及等效线性模型Fig.9 Bolted joint and equivalent linear models
通过调节螺栓预紧力实现结合部损伤,试验数据分为两个部分,第一部分测试工况如表2所示,用于寻求辨识参数与预紧力的关系。再次调整螺栓预紧力,其工况设置如表3所示,这部分数据用于试验后期验证,通过辨识参数判断预紧力大小。
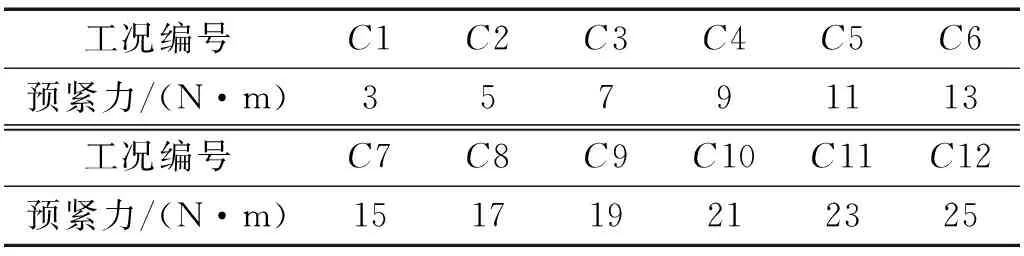
表2 用于数据拟合的工况
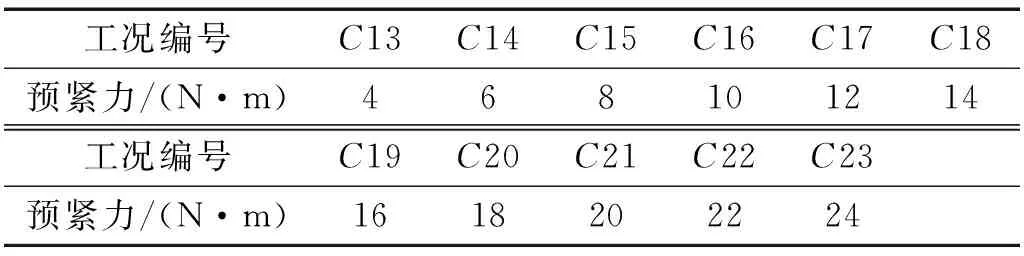
表3 用于识别预紧力的工况
不同预紧力测得的整体结构频响函数绘制,如图10所示。
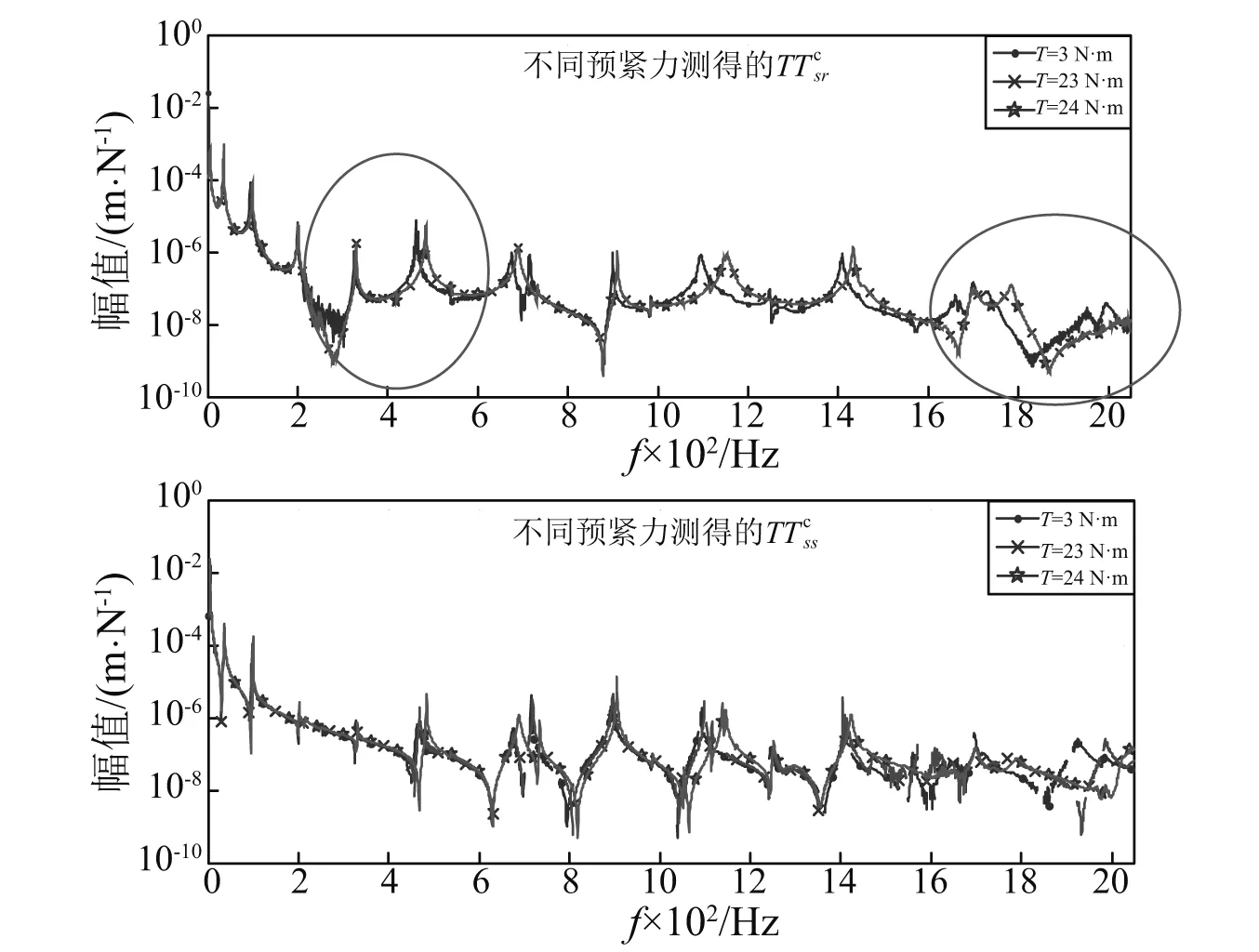
图10 整体结构频响函数Fig.10 FRFs of assembled structure
从图10可知整体结构频响函数随预紧力变化的情况:①预紧力很低,如3 N·m,结合部连接状态显著影响结构整体特性,频响函数出现毛刺,这可能是由结合部分离碰撞引起的非线性响应;②预紧力很大,如23 N·m,24 N·m,结构整体性能稳定,体现为预紧力增加,整体结构频响函数只在高频部分变化。
4.2 转动频响函数获取
试验只能测得平动方向频响函数,方程中需要转动方向频响函数,本文通过参数型有限元修正方法获取转动方向频响函数。目标函数为有限元模型与实测固有频率相对误差最小
(12)
式中:n为采用前n阶固有频率,对悬臂梁取n=7,对自由梁取n=3。修正参数为弹性模量,螺栓开孔处单元刚度、质量折减,修正结果如表4所示。修正有限元模型的固有频率和实测固有频率的差异非常小,表明实际结构的动力特性与有限元模型基本一致,因此可用有限元模型计算的频响函数代替实测频响函数。
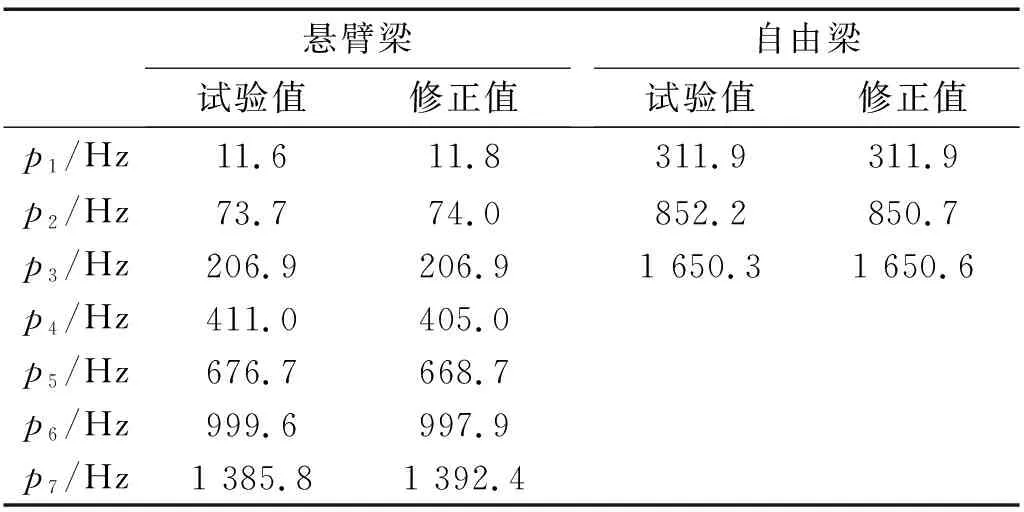
表4 固有频率试验值与有限元修正值
4.3 一组弹簧模型辨识结果
采用一组弹簧模型辨识工况1~工况12的特征参数,PSO算法中,种群粒子数为20,迭代为30次,求解域为kt∈[1×105,5×107],kr∈[1×103,5×105],结果如表5所示。
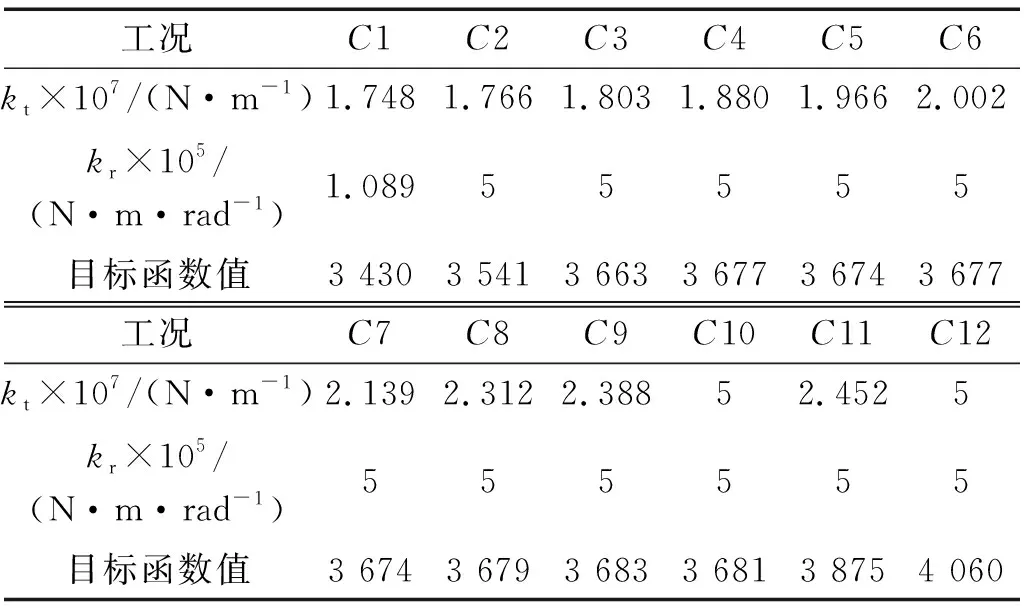
表5 一组弹簧模型辨识结果
从辨识结果中看到,目标函数值较大。实际上,线性模型与结合部真实力学模型间存在模型误差,但只要不同预紧力得到的频响函数差异能反映在参数变化上,可以通过这个关系,识别螺栓预紧力。
一组弹簧模型辨识到的扭转刚度与预紧力之间无明显规律,不能反映螺栓预紧力的变化,不适宜选作特征参数识别螺栓预紧力。竖向刚度随预紧力呈正相关关系,因此选取竖向刚度作为特征参数。
预紧力为21~25 N·m,结构整体性能稳定,整体结构频响函数只在高频部分变化,一组弹簧模型只有两个变量,模型变化不灵活,不能拟合高频段频响函数的变化。辨识参数落在边界值时使得线性模型频响函数误差与实测频响函数加权误差和最小,频响函数差异不能反映在竖向刚度变化上。
当辨识参数落在边界值时,说明实测频响函数已经趋于稳定,即预紧力较大。本文的目的是通过法向刚度辨识螺栓预紧力,对于预紧力较大的情况,预紧力变化带来的频响函数差异已经不能体现在参数变化上。因此剔除该工况10和工况12的结果,绘制竖向刚度随预紧力变化曲线,如图11所示,辨识竖向刚度随预紧力呈正相关关系,为下一步预紧力辨识做准备。
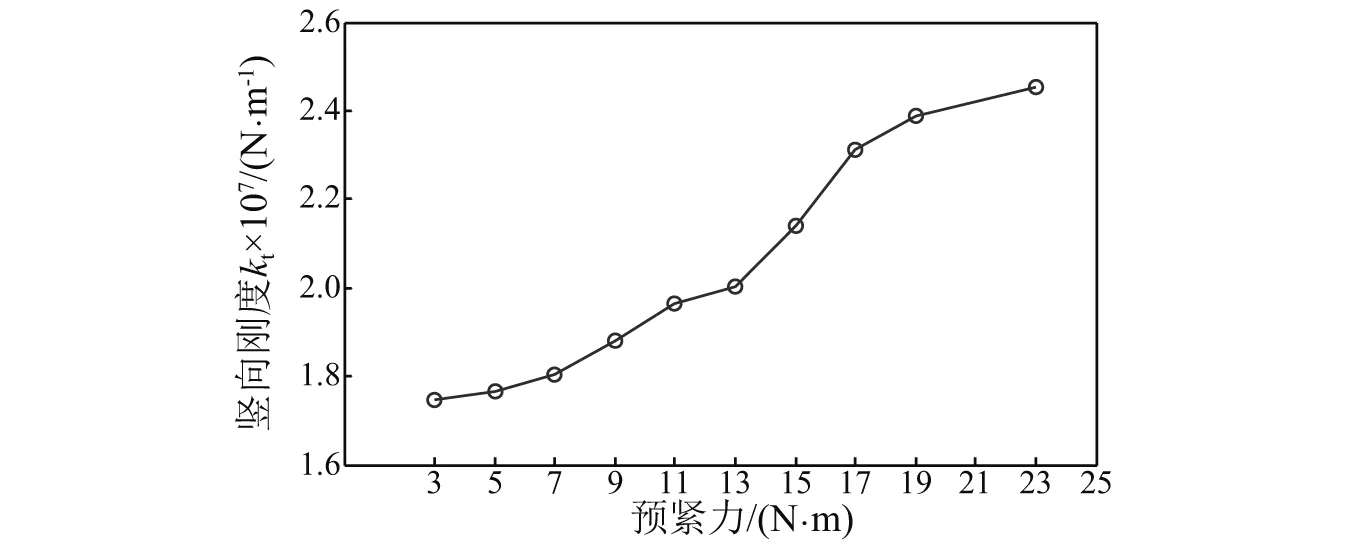
图11 一组弹簧模型,竖向刚度与预紧力关系图Fig.11 Identified stiffness for one spring model
4.4 三组弹簧模型辨识结果
采用三组弹簧模型辨识工况1~工况12的特征参数,PSO算法中,种群粒子数为20,迭代为30次,求解域kt∈[1×105,5×107],kr∈[1×103,5×105]。辨识参数为六维向量,不便于比较,取kt,kr为3个竖向刚度和扭转刚度之和,结果如表6所示。以kt特征参数,绘制竖向刚度随预紧力变化曲线,如图12所示。
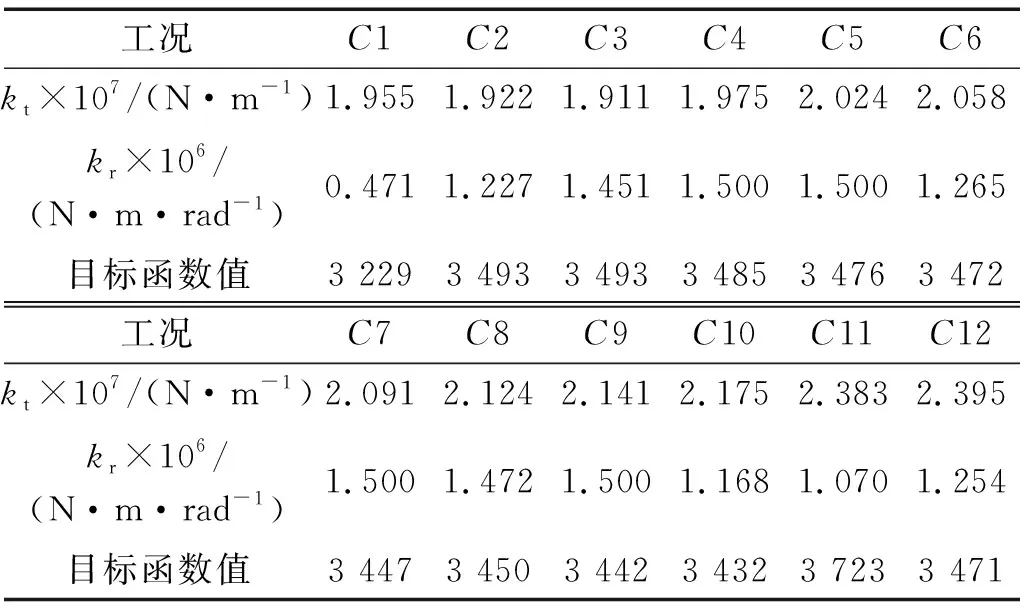
表6 三组弹簧模型辨识结果
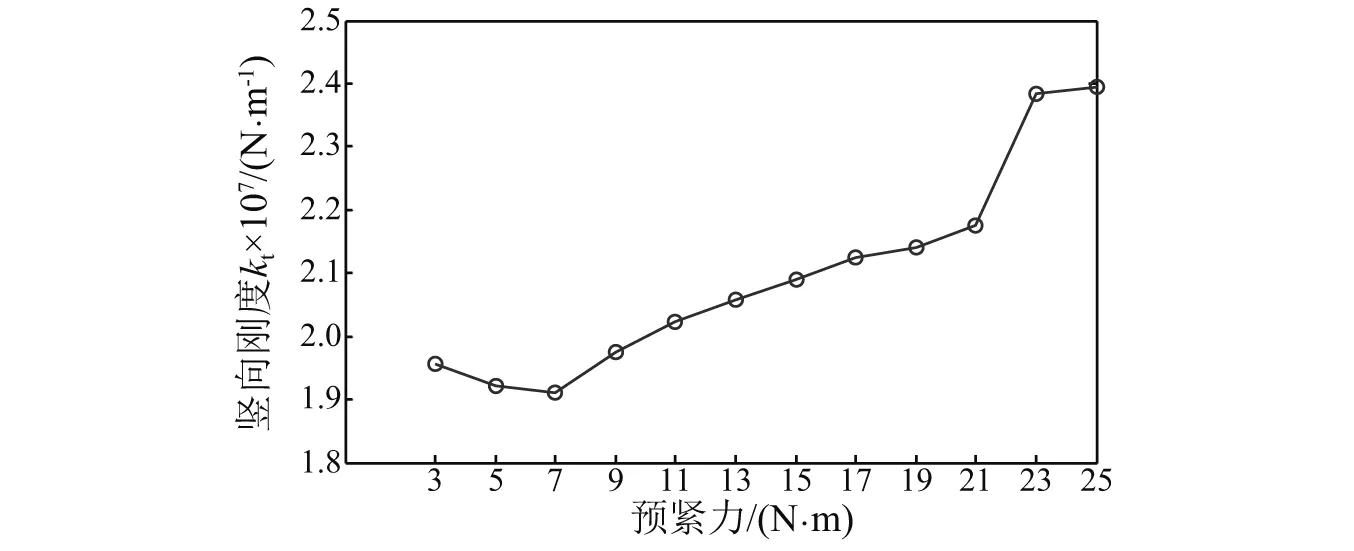
图12 三组弹簧模型,竖向刚度与预紧力关系图Fig.12 Identified stiffness for three spring models
预紧力为3~5 N·m整体结构频响函数曲线出现许多毛刺,三组弹簧模型变量多,模型灵活,除了拟合频响函数的整体特性变化外,还受频响函数毛刺部分的影响,不同预紧力的频响函数差异不能合理地反映在竖向刚度变化上。
从图11和图12中可以观察到,整体上,特征参数与预紧力间呈正相关关系,具有规律性。由于模型误差,目标函数值较大,线性模型频响函数不能与实测频响函数准确吻合。本文采用正问题求解思路,构建目标函数,采用优化算法获取使得线性模型频响函数与实测频响函数误差最小的一组参数,不要求线性模型频响函数与实测频响函数准确相等,从而降低了模型误差对辨识参数精度的影响。不同预紧力的频响函数差异反映在竖向刚度变化上,则可以通过这个关系去识别螺栓预紧力。
4.5 螺栓预紧力辨识
对一组弹簧模型、三组弹簧模型的辨识结果采用多项式对数据进行拟合。由于预紧力和刚度之间的数量级差异很大,将刚度值除以107,去除数量级的影响,再进行数据拟合。将一组弹簧模型工况10和工况12,三组弹簧模型工况1和工况2的辨识参数剔除。
数据拟合过程采用MATLAB软件内置工具箱polyfit()函数完成,其表达式如式(14)和式(15)所示。如图13和图14所示,拟合多项式得预测值与真实值比较接近,说明采用多项式对数据进行拟合是合理的。
k=kt/107
(13)
(14)
(15)
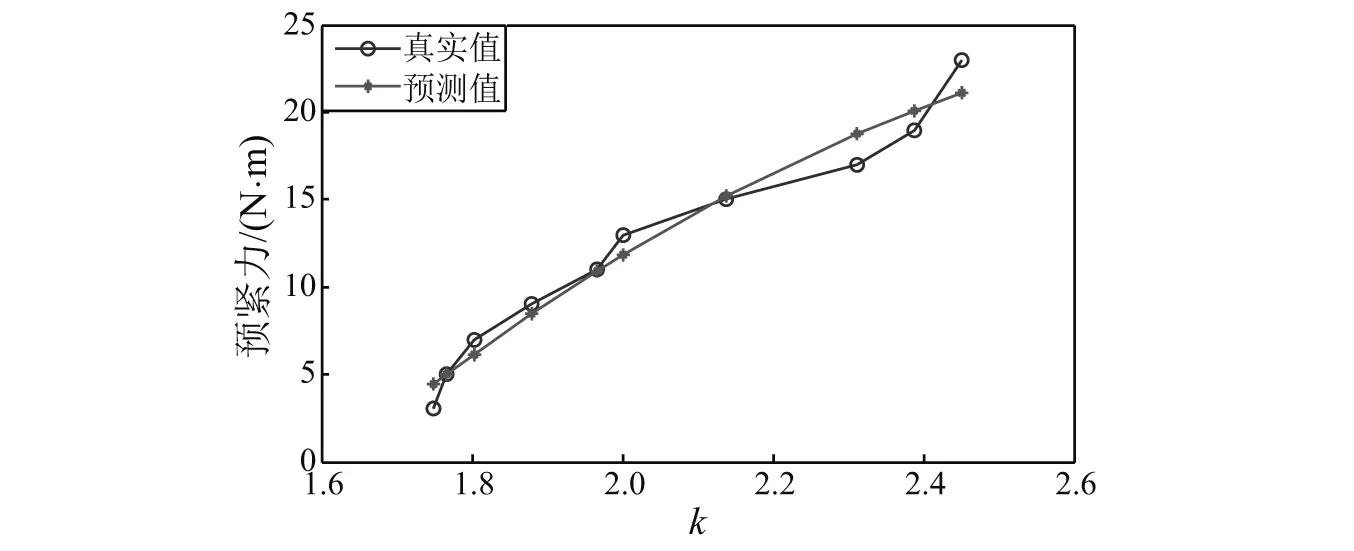
图13 一组弹簧模型预测曲线Fig.13 Predicted curve for one spring model
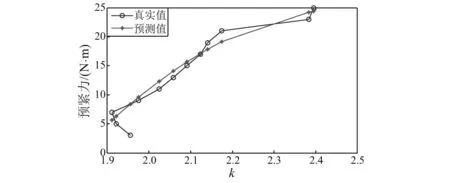
图14 三组弹簧模型预测曲线Fig.14 Predicted curve for three spring models
工况13~工况23的数据用于检验经验表达式识别螺栓预紧力的效果。对工况13~工况23的实测频响函数,分别采用一组弹簧模型和三组弹簧模型为结合部等效线性模型辨识,辨识竖向刚度如表7所示。辨识刚度是使得线性模型频响函数与实测频响函数差异最小的值。相同预紧力下,一组弹簧模型、三组弹簧模型识别的特征参数及随预紧力变化量会存在差异。实验中一组弹簧模型竖向刚度随预紧力变化量较大,三组弹簧模型竖向刚度随预紧力变化量较小,两个模型辨识刚度整体表现为随预紧力增加而递增。
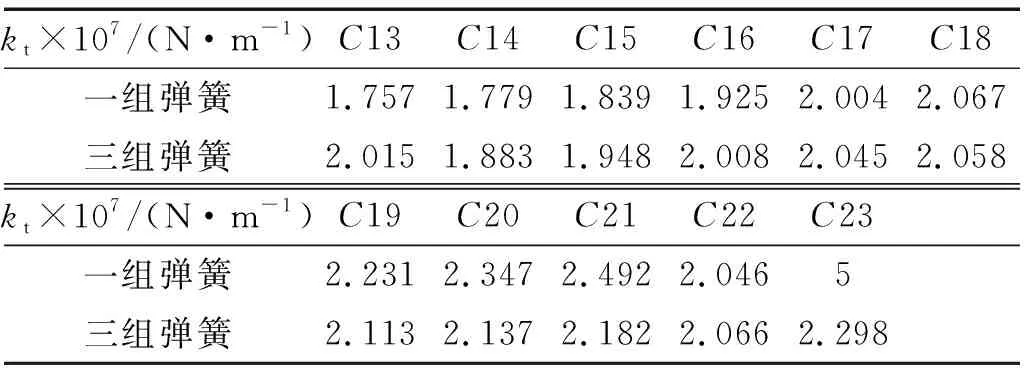
表7 工况13~工况23辨识竖向刚度
一组弹簧模型与三组弹簧模型的经验表达式和辨识参数,预测螺栓预紧力,预测结果如表8所示。
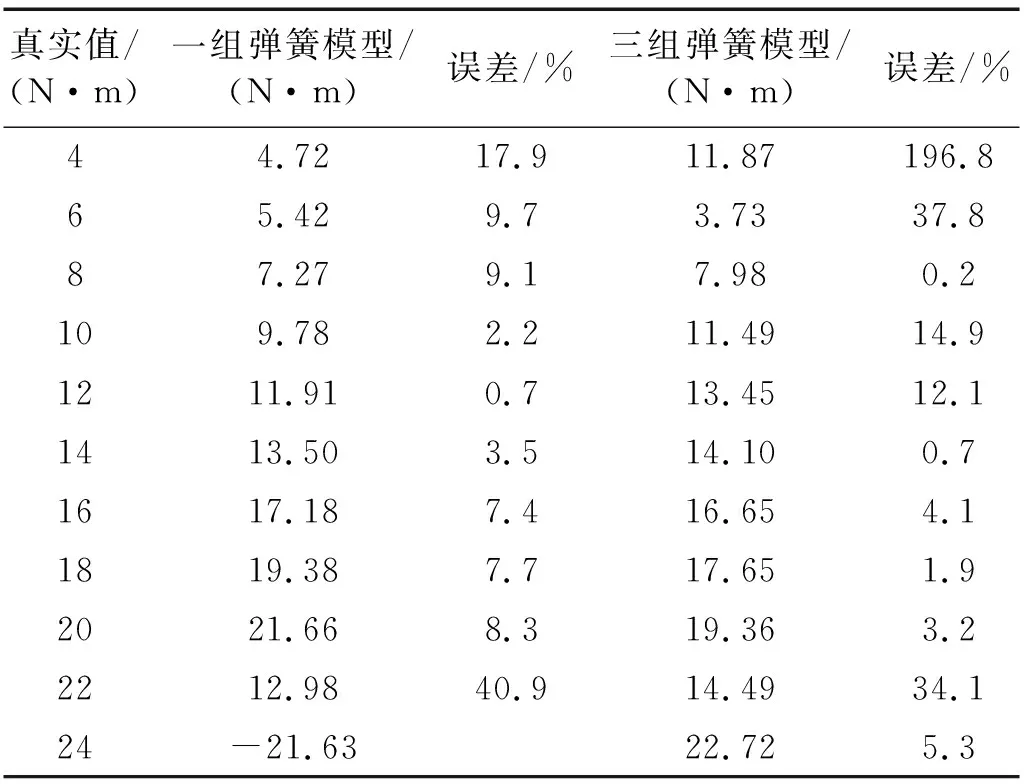
表8 工况13~工况23预紧力值
从表8的辨识结果中可以看到本文所提的方法能够准确识别螺栓预紧力。在预紧力8~20 N·m,识别精度很高,误差最小为0.2%,误差最大为14.9%。
不同预紧力下,结合部连接状态不同,受到模型误差的影响,并非整个阶段的预紧力变化都能反映在特征参数变化上。结合工况1~工况12的辨识结果,对于一组弹簧模型,在预紧力3~20 N·m,螺栓预紧力变化带来的频响函数差异能够反映在特征参数变化上,通过经验表达式,能准确预测预紧力。在预紧力22 N·m,24 N·m,整体结构频响函数只在高频部分变化,一组弹簧模型只有两个变量。线性模型与结合部真实力学模型间的误差决定了在拟合低频段频响函数的同时不能拟合高频段频响函数的变化,因此频响函数差异不能反映在特征参数变化上,无法准确识别高预紧力工况。
对于三组弹簧模型,模型变量增加,模型变得更灵活,可以反映结构局部性能变化,与结合部实际力学行为间的模型误差也发生变化。在预紧力7~25 N·m,螺栓预紧力变化带来的频响函数差异能够反映在特征参数变化上,可以准确预估螺栓预紧力。但在预紧力3~6 N·m,结合部存在非线性力学行为,表现为频响函数出现毛刺,三组弹簧模型为线性模型,通过改变参数拟合非线性力学行为,模型误差大,预紧力变化带来的频响函数差异不能合理地反映在竖向刚度变化上。一组弹簧模型变量较少,主要拟合频响函数的整体特性变化,而忽略频响函数中的毛刺带来的影响,模型误差反而更小。此外工况C22中,两组模型辨识的预紧力误差均较大,这可能是由于测量误差引起的。
虽然不同线性模型处理模型误差的能力不同,辨识精度也不完全相同,但基于本文采用的方法在参数识别过程中不要求线性模型频响函数与实际频响函数准确相等,在模型误差影响下,只要目标函数仍能保持在结合部参数中取得最小值,则能准确辨识特征参数。通过试验验证表明,本文所构建的目标函数具有很高的鲁棒性,能在一定程度上克服模型误差和测量误差带来的影响,解决了参数辨识的不适定性,通过经验表达式能准确识别螺栓预紧力。
5 结 论
本文通过数值仿真和试验,研究了栓接结合部等效线性模型的参数辨识问题,建立了鲁棒性高的目标函数,分析了结合部等效线性模型建模问题,实现了栓接结合部损伤的定量评估,总结全文得到如下结论:
(1) 基于频响函数辨识法,本文对方程组进行加权处理,避免求逆运算,构建目标函数进行参数辨识,获取使得线性模型频响函数与实测频响函数加权误差最小的一组参数,不要求线性模型频响函数与实测频响函数准确相等。数值仿真中,5%噪声下,辨识参数误差低于1%;10%噪声下,误差低于4%;试验研究中,在噪声与模型误差影响下,辨识参数能够准确反映螺栓预紧力变化情况。说明本文所提方法较好地解决了参数辨识的不适定性问题,具有良好的鲁棒性。
(2) 本文尝试用等效线性模型特征参数定量评估栓接结合部螺栓预紧力。结合部连接竖向刚度与螺栓预紧力关系可用多项式拟合,该关系式可准确预测螺栓预紧力,在预紧力为8~20 N·m的工况,三组弹簧模型识别结果中,最大误差为14.9%,最小误差仅有0.2%。
(3) 试验研究中,随着预紧力降低,结合部连接状态初始线性状态转化到非线性状态,单一个线性模型难以准确定量评估全部连接状态下的螺栓预紧力。弹簧数量少的模型变化不灵活,不能反映频响函数细微变化,因此不能识别螺栓预紧力高的情况。弹簧数量多的模型变化灵活,会拟合结合部非线性力学行为带来的频响函数改变,不能识别预紧力低的情况。还需要对结合部等效模型连接节点数目及分布进行研究。
