椭圆曲率半径的四个公式及两种力学推理方法

邵 云

(南京晓庄学院电子工程学院，江苏 南京 211171)

赤峰学院李景琴老师曾在文献[1,2]中分别利用：(1)椭圆规尺[3]上任一点的运动，(2)光滑水平面上内含竖直光滑圆形轨道的滑块内质点的下滑运动，(3)相互垂直的两简谐运动的合成，来构造不同情形的椭圆运动，计算出各自的速度矢量和加速度矢量a，分解出法向加速度分量an，进而利用公式an=v2/ρ推算出椭圆的曲率半径ρ。鄂尔多斯第一中学的宋辉武老师则是通过构造匀速率椭圆运动来推算椭圆的曲率半径[4]，并将此匀速率构造方案推广至其他一些曲线曲率半径的推算[5]。淮北第一中学的王化银老师将以上运动学推理方法简化成一个统一的矢量计算公式：省去了矢量投影的麻烦，使得推算过程简单了许多。诸位老师采用的运动学推理思路基本相同，ρ的结果均为直角坐标形式，因此显得思路不够开阔。本文首先根据高等数学中二维曲线曲率半径的计算公式，逐步推得椭圆曲率半径的两种直角坐标和两种极坐标形式的公式；然后分别应用力学中匀速率圆周运动投影的运动学方法和行星沿椭圆轨道运动时的动力学结论——能量守恒定律与角动量守恒定律，结合法向加速度分量公式，分别推导出椭圆直角坐标和极坐标形式的曲率半径。

1 应用曲率半径的数学公式推导椭圆的曲率半径

在高等数学中，二维曲线y=y(x)的曲率半径公式是

(1)

(2)

图1 正椭圆及其准线

其中a、b分别为椭圆的半长轴、半短轴，图中c为半焦距，下同。将式(2)两边对变量x求导，经整理可得

(3)

将式(3)两边对变量x求导，并将式(3)代入可得

(4)

将椭圆方程式(2)代入即得

(5)

于是，将式(3)、式(5)代入式(1)即得该正椭圆的曲率半径：

(6)

若将椭圆方程式(2)代入式(6)，消去y后又可得

(7)

这时ρ显示为x的一元函数。式(7)中的e=c/a是椭圆的偏心率。

参见图1，由准线知识知，椭圆上任一点距离右焦点的距离

(8)

将式(8)代入式(7)消去x后可得

(9)

这便是极坐标形式的椭圆曲率半径公式，ρ由极坐标r唯一地确定。

此外，参见图1，由于2a-r=r′，所以式(9)又可改写成

(10)

这即为椭圆曲率半径的最简公式，它兼具对称性，因此最方便记忆。

式(6)、式(7)、式(9)、式(10)是椭圆曲率半径的四个公式，其中式(6)最为常见，式(7)、式(9)最方便使用，式(10)则最便于记忆。

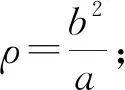
2 应用匀速率圆周运动投影的方法求椭圆的曲率半径

如图2、图3所示，将图2中斜面上的匀速率圆周运动在水平面内投影，即得一变速率椭圆运动，见图3。斜面的倾角θ满足cosθ=b/a。

图2 斜面上的匀速率圆周运动

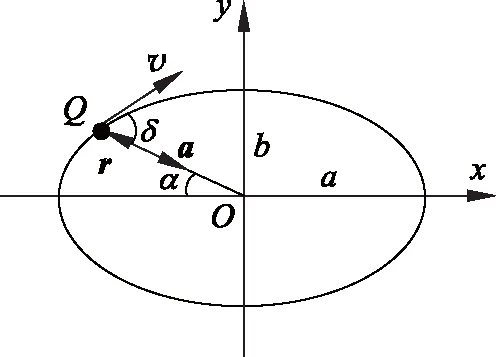
图3 水平面内的投影椭圆运动

在图2的坐标系O′-x′y′中，运动质点P的位置矢量r′可表示成

r′=a(-cosφi′+sinφj′)

(11)

其中i′、j′分别是两坐标轴正方向上的单位矢量。质点P的速度矢量′和加速度(即法向加速度)矢量a′分别可表示成

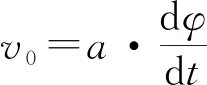
设图3中坐标系O-xy的单位矢量分别为i、j。分析可知：斜面上的单位矢量i′在水平面内的投影就是i，而j′在水平面内的投影则是cosθj。于是斜面上质点P的r′、′和a′在水平面内的投影分别为

这些便是质点P在水平面内的投影点Q的位矢、速度、加速度的矢量表达式，见图3。虽然Q并非质点，但其运动学方程式(14)～式(16)具有与式(11)～式(13)相同的意义，只是对应量的夹角有所变化，如图3中所示。

由式(15)可得

(17)

从图3可见，投影点Q的法向加速度分量(图中未画出)为

an=|a|sinδ

(18)

其中将加速度大小记作|a|是为了与椭圆半长轴a区别。利用矢量矢积的知识知

(19)

将式(15)、式(16)代入式(19)，并将结果代入式(18)后可得

(20)

由式(17)和式(20)即得图3中Q点处的曲率半径：

(21)

(6)

综上可见，这里采用匀速率圆周运动的速度、加速度投影的方法来计算椭圆的曲率半径是可行的。与其他文献中情形类似，投影点Q的速度、加速度能被计算出来是必要的前提。此处方法的优点在于思路简单，图像清晰，便于掌握和记忆。

3 应用行星的椭圆轨道运动知识求椭圆的曲率半径

3.1 行星的椭圆轨道运动相关知识

如图4所示，设太阳位于椭圆轨道的右焦点F2处，质量为M；设行星P的质量为m，其相对于力心F2(即太阳)的位置矢量r、速度及相关夹角如图4所示；设行星在近日点的速率为v1，远日点的速率为v2，则根据能量守恒定律和对力心F2的角动量守恒定律有

图4 行星的椭圆轨道运动

其中E、J分别为行星椭圆轨道运动的机械能、角动量。联立式(22)和式(23)可解得

进而求得

对于图4中任意位置的行星，同样有能量守恒定律和角动量守恒定律：

成立，其中vsinδ是行星相对于力心F2(即太阳)的横向速度分量大小。将式(26)、式(27)分别代入式(28)、式(29)，经计算可得

3.2 行星椭圆轨道曲率半径的计算

(32)

鉴于图4中δ+ψ=90°，因此有

(33)

联立式(30)、式(31)和式(33)，并应用法向加速度分量公式，即得椭圆轨道的曲率半径：

(34)

这与前文用数学公式算得的式(9)一致。

需要指出的是，本节采用的基本是动力学的推理思路，它与第2节的运动学推理思路有所区别。另外，需要说明的是，虽然行星椭圆轨道的曲率半径仅通过以上的初等数学就能推算出来，但是行星椭圆轨道本身的论证却依赖于复杂的微积分运算[3]。

4 力学中曲率半径的由来及其几何与代数表达式的等价性

鉴于质点在任意时刻的三维瞬间运动总可被看作此刻密切平面(注：所谓“密切平面”是指三维曲线上某位置处无限接近的相邻的3个点所确定的极限平面。)内的一小段二维圆弧运动，且加速度a仅在此密切平面内有分量[3]，因此一般的力学教科书都是通过图5对作二维曲线运动的质点P的加速度进行推理，然后再将结果推广至三维曲线运动。图5中已建立了平面直角坐标系O-xy、平面自然坐标系et-en及自然坐标轴O′s，同时也标出了质点P的平面自然坐标s和θ，等效短圆弧运动的弧长ds和圆心角dθ，以及切向单位矢量et的无穷小增量det。

图5 质点平面曲线运动的微分析图

根据力学知识，质点P的加速度为

(35)

由图5可见，det的方向总是沿着法向单位矢量en的方向，且有

det=|dθ|·en

(36)

这里|dθ|是较严格的写法。将式(36)代入式(35)，稍加变换即得质点在平面(或空间)自然坐标系中的加速度：

(37)

由图5又可见，

对式(39)两边微分得

sec2θdθ=dy′=y″dx

(40)

将式(39)代入式(40)得

(41)

(1)

由此可见，力学中ρ的几何定义式与高等数学中ρ的代数表达式是等价的。

5 结语

应用力学知识推导二维(或三维)曲线的曲率半径，向来都是通过法向加速度分量公式an=v2/ρ进行的，只要能够将曲线上某一(或任一)位置质点(或某种数学点)的运动速度、法向加速度分量an求出来，即可通过该公式求出某点(或任一点)处的曲率半径。该力学方法对曲线的形状、曲线上质点(或几何点)的运动状况均没有特殊的要求。

从上文第4节可见，法向加速度分量公式中所引入的曲率半径正是数学意义上的曲率半径，换言之，曲率半径这个数学量已经有机地融入到牛顿力学的体系当中。我们既可以借助于质点运动学的知识求出轨迹的曲率半径(属多数情况，如文献[1,2,4-6]及本文第2节等)，又可以借助于质点动力学的某些实际结论求出之(如本文第3节等)。

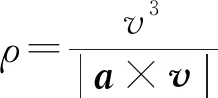
最后，需要说明的是，牛顿力学是建立在微积分和矢量几何基础上的一门物理学科，利用它推理一些数学公式或结论，本质上是利用牛顿力学内在的物理逻辑和几何逻辑去推证另一些数学逻辑或结论，这正体现了数理体系内在的一致性和自洽性。