最速降线及其等时性

郑 琦

(浙江省萧山中学，浙江 杭州 311201)

摆线在物理和数学中的应用非常广泛，文[1]、文[2]中给出了摆线的许多有趣的性质，文[3]则对这些性质做出了物理上的解释，摆线问题最早来自于伽利略(Galilei)在1630年提出的最速降线问题。

如图1所示，小球从A点静止释放，沿光滑轨道AB滑下到达B点，要求用时t最短，试确定轨道AB的方程。

图1

1696年约翰·伯努利(Johann Bernouli)就此问题向全欧洲提出挑战。牛顿(Newton)、莱布尼兹(Leibniz)、雅克比·伯努利(Jakob Bernouli)、洛必达(L’Hpital)等人都给出了答案，他们得出了相同的结论：最速降线就是摆线(也叫圆滚线、旋轮线)。惠更斯(Huggens)则从等时性上研究，发现等时降落的解也是摆线。Johann和Jakob的解法略有不同，Johann利用费马原理来快速求解，Jakob的解法较为复杂但更具一般性，兄弟两人为此争执了许多年，后来Johann的学生Leonhard Euler吸收了背后的思想和精华，创立了泛函分析中极为重要的变分法。

本文尝试从一般的折射定律出发给出轨迹方程，然后讨论该轨迹方程的物理意义，最后通过轨迹方程的数学处理来证明等时性。

1 轨迹方程的求解

如图2所示，当小球下降y时的速度为

(1)

图2

将小球的运动类比成光的连续折射现象。将竖直平面分割成无数个水平的小区域，每个区域内的折射率n相同。在y处的折射率为

(2)

如图3所示，在任意某个分界面由光的折射定律可得：

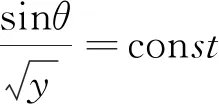
(3)

图3

又由于

(4)

联立式(5)、式(6)，可得：

y(1+y′2)=A

(5)

其中A为某个待定常数，其解为

式(6.1)和式(6.2)正是所求的轨迹方程。

2 物理意义

式(6.1)和式(6.2)所描绘的曲线就是一条摆线，它对应的物理过程如图4所示，半径为R的圆环以速度v0向右做纯滚动，轮上一点P的轨迹刚好就是这条摆线。

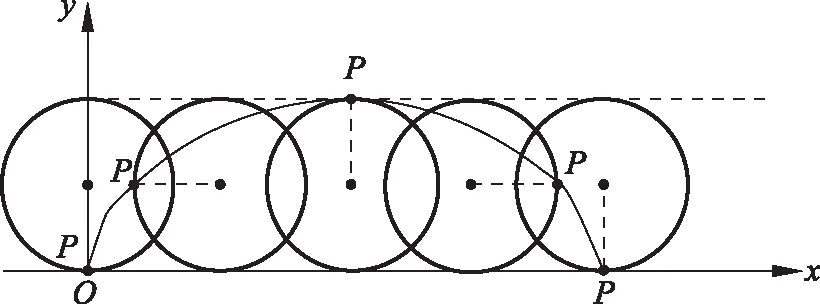
图4

图5

如图5所示，取t=0时刻，P刚好位于圆环中心的正下方，经过时间t，圆心的水平坐标为：xC=v0t=Rφ。此时P与竖直线成φ角，P的位置坐标为：

3 等时性的证明

摆线等时性的证明往往采用将其与简谐运动等价从而证明等时性，本文试图采用更加数学的办法来同样证明此结论。

图6

3.1 A点的速度

将式(6.1)和式(6.2)对时间求导，可得A点速度为

(7)

比较式(1)和式(7)可知：代入B点可得：

(8)

(9)

3.2 弧长ds

(10)

由式(6.1)和式(6.2)可得：

(11)

3.3 时间t

(12)

积分：

(13)

由于A为抛出点，所以φA=0，即

(14)

这与文[3]、文[4]利用简谐运动证明等时性的结论是一致的。