结合滑动窗口与模糊互信息的多标记流特征选择
2019-02-15程玉胜王一宾
程玉胜,李 雨,王一宾,3,陈 飞
1(安庆师范大学 计算机与信息院,安徽 安庆 246011) 2(数据科学与智能应用福建省高校重点实验室,福建 漳州 363000) 3(安徽省高校智能感知与计算重点实验室,安徽 安庆 246011)
1 引 言
多标记学习是机器学习、数据挖掘、模式识别等人工智能领域的研究热点之一,能很好的解决现实生活中多义性问题.在多标记学习框架之下,特征数据往往面临着高维性[1-3]的问题,使得一般的手工标记费时费力,不仅如此,高维数据也会严重影响分类器的分类精度[4-6].但如果利用标记的相关性对特征进行选择,无疑会很好的解决上述问题.
目前,Lee等[7]提出了基于多变量互信息的多标记特征选择算法(Pairwise Multivariate Mutual Information,PMU),其算法是通过选择与标记空间互信息最大的特征,生成特征子集.Lin等[8]提出了基于邻域互信息的特征选择算法(Multi-label feature selection based on neighborhood mutual information,MFNMI),其算法基于三种不同的观点,首先计算特征与标记空间的互信息大小,选择与标记空间互信息最大、与已选特征冗余性最小的特征生成特征子集.Zhang等[9]提出了基于最大相关性的属性约简算法(Multi-Label Dimensionality Reduction via Dependence Maximization,MDDM),其算法利用两种投影策略,根据原始特征与标记空间最大相关性将原始数据投影到较低维的特征空间.Zhang等[10]提出的多标签朴素贝叶斯分类的特征选择算法(Feature selection for multi-label naive Bayes classification,MLNB)等.
另外,上述常见的特征选择算法都无法处理动态或者增量数据,然而现实世界中有些实例的特征无法一次性全部获取,数据是实时产生并记录的,例如患者诊断就是医生不断的诊断检查再诊断检查,最后才确定患者的病因病情的过程.我们把这种特征逐渐增加的过程称为流特征.传统的特征选择算法,无法解决具有流特征[11-14]问题的特征选择.滑动窗口[15,16]机制能很好的解决该问题.目前滑动窗口主要集中在数据流聚类和特征选择[17-19]算法研究中,如Guha等[20]提出了STREAM算法,该算法是针对数据流聚类的典型算法,其根据分治原理,在有限的空间对数据流进行聚类.常建龙等[16]提出了基于滑动窗口的数据流聚类算法CluWin,该算法不仅研究了拒伪和纳真误差滑动窗口模型中的聚类问题,还将其推广用于解决N-n窗口内的数据流聚类的问题,针对数据流环境下特征选择还主要以单标记特征选择为主,对多标记学习中流特征选择研究还不多.
同时不难发现,在常见的特征选择算法中,目前主要还是基于信息熵方法计算特征与标记之间的相关性较多,但这种方法主要基于香农熵也即传统信息熵[21-23]方法,该方法不具有补的性质,因此计算过程较为复杂.上述大部分特征选择算法中都利用互信息作为启发式函数来选择重要特征,一般来说互信息越大其特征越重要.然而,香农信息熵计算“只计字数、不计内容”,撇开了人的主观因素和信息本身的含义,如果结合实际情况考虑一个有意义的因素,定量地给出该事件相应的权重,那么修正的加权熵就更有意义[24,25],为了解决这种问题,在模糊信息熵的方法基础上,本文重新构造了重要度目标函数:首先对互信息进行了加权处理,然后对其进行正则化,并且正则化处理依次在有限大小的窗口中进行.
针对上述问题,本文提出了结合滑动窗口与模糊互信息流特征选择算法,首先将滑动窗口应用到多标记学习的特征选择上,根据判断条件将满足条件的特征保存下来,随着特征的不断流入,窗口也向前滑动.其次,引入粗糙集理论修正了传统的信息熵,并用新的重要度目标函数度量特征与标记之间的相关性.最后,本文进行了大量实验,实验结果表明本文算法是有效的,并采用统计假设检验对本文算法进行了有效性检验.
2 多标记学习及其模糊信息熵
2.1 多标记学习框架
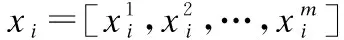
2.2 模糊信息熵

(1)
信息熵是度量随机变量不确定性的程度,信息熵越大就表示随机变量不确定性程度越大,在多标记的特征选择算法中,常常利用传统信息熵来选择特征空间中与整个标记空间互信息大的特征,但传统信息熵不具有补的性质,基于传统的信息熵,利用粗糙集理论等价划分的思想,引入模糊信息熵的新定义.
定义2.[23,27]假设信息系统由样本及其对应的特征所描述,把样本空间的描述记为论域U,根据某种特征属性可以对论域U进行划分,假设按照特征属性F={f1,f2,…,fn}对论域U进行划分记U/F=X={X1,X2,…,Xm},则模糊信息熵定义如下:
(2)
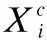
(3)
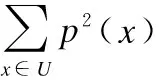

在多标记学习中,按照特征属性对论域U划分记为X={X1,X2,…,Xm},按照标记属性对论域U的划分记为Y={Y1,Y2,…,Yn},类似于传统的条件信息熵,模糊条件熵[27]定义如下:
定义3.[23,27]
(4)
定义4.[23,27]类似的,模糊互信息定义为:
(5)
模糊自信息熵、条件熵以及模糊互信息之间满足如下关系:
E(Y;X)=E(Y)-E(Y|X)
(6)

=E(Y;X)+E(Y|X)
所以,E(Y;X)=E(Y)-E(Y|X)成立.
2.3 一种新的重要度目标函数
目前,很多算法都利用特征与标记空间之间的互信息来判断特征是否为重要特征,然而互信息最大的特征可能并不是最重要的特征,为了避免过拟合,我们先对互信息进行加权,然后对其进行正则化处理,构造的函数如下:
(7)

3 基于滑动窗口的流特征选择
3.1 滑动窗口机制
滑动窗口一般有两个端点,分别确定这个窗口的起始位置和终止位置,如图1滑动窗口模型[18,19],每一个新的数据流入滑动窗口时,滑动窗口的前端和末端都会同时向前移动,在依次向前滑动的过程中,根据窗口内数据个数是否发生变化可将滑动窗口分为窗口大小固定和窗口大小可变两种形式,一般地,每到达一个新的数据时,滑动窗口的前端和末端同时向前移动一个位置.本文设定两个窗口大小固定的窗口,即处理窗口和存储窗口,特征进入的窗口即为处理窗口,处理窗口的大小设为W,处理窗口是动态的,每当一个新的特征到达时,处理窗口整体会向前滑动一个位置,而原处理窗口最末端的数据被删除.保留重要特征的窗口即为存储窗口,存储窗口的大小设为H,存储窗口是固定的,不随着新特征的到达而移动.假设滑动窗口的传输方向是自左向右,如图1所示.

图1 滑动窗口模型Fig.1 Sliding window model
实际情况中每个特征流入滑动窗口中的时间间隔并不是相等的,由于滑动窗口大小是固定的,所以如果仅以相等的时间间隔向后移动窗口是不合理的,窗口大小固定的滑动窗口是在按照时间顺序的基础上以窗口大小W为单位依次向后移动,如果某一时刻,特征同时到达的个数几乎不止一个,那么这个时候我们应该尽可能的精确时间,使得每个特征到达的顺序是相差一定时间的.
3.2 结合滑动窗口与模糊互信息的多标记流特征选择
在本文所提出的结合滑动窗口的模糊互信息流特征选择算法中,利用滑动窗口对特征的模糊互信息进行正则化处理,以减小模糊互信息对特征重要程度判断的影响,防止过度拟合,采用正则化方法会自动削弱不重要的特征变量.首先将特征空间中的特征作为流特征,按照特征排序的顺序依次进入滑动窗口,特征在进入固定大小的滑动窗口后计算特征与整个标记空间的模糊互信息大小,然后根据公式(7)的特征重要程度目标函数依次计算其值的大小,所得的值越大就表示其特征越重要,特征保存到存储窗口后并在存储窗口内根据重要程度由小到大依次进行排序,当存储窗口H中的特征个数达到了窗口大小时,窗口仍然向后滑动,如果下一时刻进入的特征的重要程度比存储窗口中的第一个特征大,那么新进入的特征将取代第一个特征,依次循环,直到最后一个特征进入窗口中,最后,将存储窗口H的特征序列构成特征子集.
根据上述描述,结合滑动窗口与模糊互信息的多标记流特征选择(Multi-labelStreamingFeatureSelection combiningSlidingWindow andFuzzyMutualInformation:SFS-FMI-SW)
描述如下:
输入: 处理窗口的大小W,存储窗口的大小H,多标记学习数据集T.
输出:ti时刻所产生的特征子集f.
1)ti时刻产生的特征fi;
2) while |f|≤H,do
3) for eachfi∈F;
4) for eachlj∈L;
5) 根据公式(2)计算E(fi;lj) ;
6) end;

8) 根据流特征与标记空间的模糊互信息利用公式(7)计算特征的重要程度目标函数para(i);
9) 特征进入存储窗口中根据公式(7)的值的大小依次从小到大进行排序;
10) end
11)end while;
12) for i=H+1:m
13) 如果新流入的特征的重要程度比存储窗口中任一特征重要;
14) 那么将新特征代替存储窗口中的那个特征;
15) 存储窗口内的特征根据重要程度自动进行排序;
16) end;
17)返回存储窗口H中的所有特征作为特征子集f.
4 实验数据及其结果分析
4.1 实验数据
本文采用了Yeast、Birds、Cal500、Artificial、Reference、Health、Business、Science这8个数据集来验证本文算法的有效性.各数据集的相关信息见表1.数据均来自于http://mulan.sourceforge.net / datasets.html.
4.2 评价指标
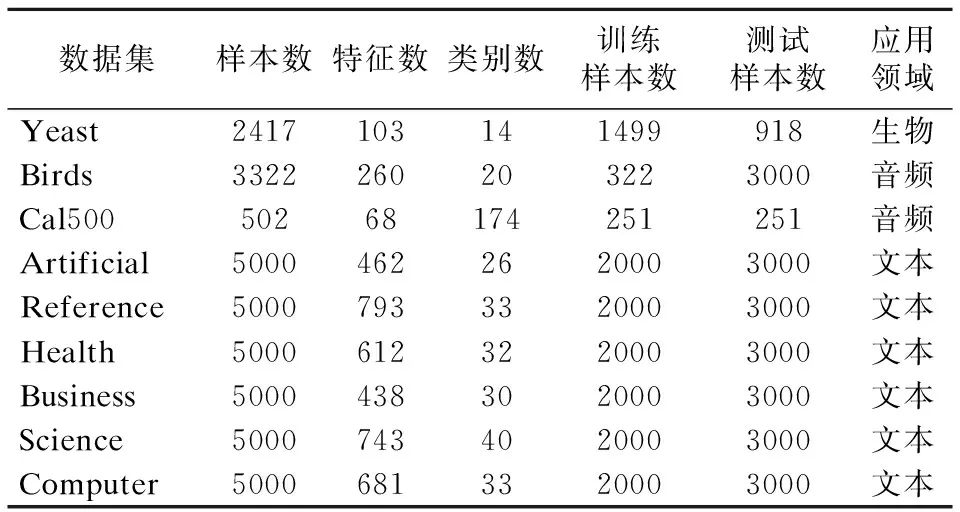
表1 多标记数据集Table 1 Multi-label datasets
为了验证该算法的有效性,利用海明损失(Hamming Loss,HL),1-错误(One Error,OE)和覆盖率(Coverage,CV),排位损失(Ranking Loss,RL),平均准确率(Average Precision,AP)这5个评价指标[10]对实验结果进行验证.样本多标记测试集:T={(xi,Yi)|i=1,2,…,p},由算法预测得到的标记集合记为h(x).
Hamming Loss:
(8)
公式(8)中Δ用于计算集合Yi和h(xi)的对称差,即对集合进行布尔逻辑中的异或操作,该评价指标用于评估样本在单个标记上的误分类情况,HL(h)越小则表示分类器h(x)性能越优,最优值为0.
One Error:

(9)
公式(9)中f(xi,y)为分类器h(x)对应的实值函数,该评价指标用于考察样本的标记排序序列中位于第一位的标记不属于样本相关标记集合的次数情况.OE(f)越小则表示分类器h(x)性能越优,最优值为0.
Coverage:
(10)
公式(10)rankf(xi,y) 是与实值函数f(xi,y) 对应的排序函数.该评价指标用于考察在样本标记排序中,覆盖所有相关标记所需的搜索深度情况.CV(f) 越小则表示分类器h(x)性能越优,最优值为0.
Ranking Loss:
(11)
Average Precision:
(12)
该评价指标用于考察在样本的类别标记排序序列中,排在给定样本标记之前的标记仍属于该样本标记概率的均值,该指标取值越大分类器h(x)性能越优,其最优值为1.
4.3 实验结果及分析
实验代码均在Matlab2012b中运行,硬件环境Inter®CoreTM i5-3230 2.6GHz CPU,4G内存;操作系统为Windows 7.本文的实验是以kNN作为分类器,对比算法有基于多变量互信息的多标记特征选择算法(Pairwise Multivariate Mutual Information,PMU)、基于最大相关性降低多标记维度(Multi-Label Dimensionality Reduction via Dependence Maximization,MDDM)、基于邻域互信息的特征选择算法(Multi-label feature selection based on neighborhood mutual information,MFNMI)、多标签朴素贝叶斯分类的特征选择算法(Feature selection for multi-label naïve Bayes classification,MLNB).kNN[28]参数值设定为默认值,即平滑系数s=1,k=10.表中↑表示指标数值越大越好,↓表示指标数值越小越好,实验结果后的符号“√”表示每个数据集在所有算法上取得的最好结果,本文算法只与MLNB、MDDMspc、MDDMproj、PMU、MFNMIpes对比时取得最好的结果用黑体字表示.各实验结果后面“()”内的值表示每个数据集在各算法上的排序.为了验证算法的有效性,随机记录一组实验,实验中处理窗口大小W设置为100,本文是基于固定滑动窗口的流特征选择算法,因此依次达到的特征也是随机的,运行十次,最终的结果以十次的平均值来代替.所有算法的特征子集大小都与MLNB所选的特征子集大小相等.
实验结果如下:
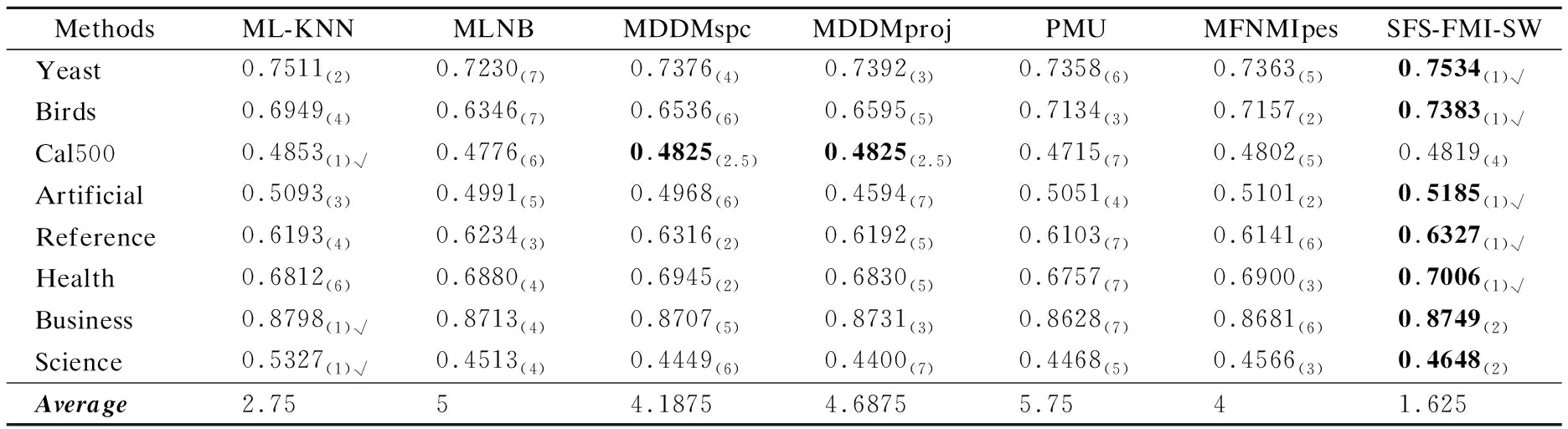
表2 在平均精度上五个特征选择算法的排名Table 2 Ranks among five feature selection methods in Average Precision(↑)
1)由表2可发现:本文算法与MLNB、MDDMspc、MDDMproj、PMU、MFNMIpes这5个算法进行对比时,在8个数据集上,本文提出的算法SFS-FMI-SW在其中7个数据集上Average Precision值最大,即性能最好;Cal500数据集上SFS-FMI-SW算法的AP值的大小仅比MDDM算法的AP值少0.0006,这表示SFS-FMI-SW算法的性能非常稳定.本文算法与所有算法进行对比时,在8个数据集上有5个数据集的Average Precision值最大.根据8个数据集上的平均排序结果可以看出,SFS-FMI-SW位列第一,ML-KNN排在第二,PMU排在最后,性能最差.

表3 在海明损失上五个特征选择算法的排名Table 3 Ranks among five feature selection methods in Hamming Loss (↓)
2)表3实验结果表明:本文算法与MLNB、MDDMspc、MDDMproj、PMU、MFNMIpes这5个算法进行对比时,8个数据集中有4个数据集SFS-FMI-SW性能优于其他算法,在数据集Cal500上,MDDMspc和MDDMproj算法的Hamming Loss值相对于SFS-FMI-SW减少仅0.0004,在Artificial数据集上,MFNMIpes的Hamming Loss值只比SFS-FMI-SW算法减少了0.0012.本文算法与所有算法进行对比时,有3个数据集的Hamming Loss值最小,在Cal500和Artificial这两个数据集上,本文算法与ML-KNN的Hamming Loss值大小相同,在其他3个数据集上Hamming Loss值与其他算法相差甚小.在Hamming Loss指标上,SFS-FMI-SW排名第1,性能最好.

表4 在1-错误上五个特征选择算法的排名Table 4 Ranks among five feature selection methods in One Error (↓)
3)表4的结果表明:本文算法与MLNB、MDDMspc、MDDMproj、PMU、MFNMIpes这五个算法进行对比时,有7个数据集上SFS-FMI-SW算法的One-Error值都是最小的,在数据集Artificial上,MFNMIpes的One-Error值只比SFS-FMI-SW减少了0.0077.本文算法与所有算法进行对比时,在8个数据集上有5个数据集的One-Error值最大,其他3个数据集的One-Error值都排在第二位.这表明算法SFS-FMI-SW的性能很好,在One-Error指标上,SFS-FMI-SW排名第1.

表5 在排位损失上五个特征选择算法的排名Table 5 Ranks among five feature selection methods in Ranking Loss (↓)
4)从表5可看出,本文算法与MLNB、MDDMspc、MDDMproj、PMU、MFNMIpes这五个算法进行对比时,算法SFS-FMI-SW在5个数据集上Ranking Loss值最小,也即性能最好,在数据集Reference上,MDDMspc只比SFS-FMI-SW的Ranking Loss值减少了0.0003,在Health数据集上,MDDMspc比SFS-FMI-SW的Ranking Loss值也只减少了0.0014.本文算法与所有算法进行对比时,有3个数据集的Ranking Loss值最小,Cal500、Artificial和Science这3个数据集的Ranking Loss值排在第2位.在8个数据集上的综合排位中,SFS-FMI-SW排在第1.

表6 在覆盖率上五个特征选择算法的排名Table 6 Ranks among five feature selection methods in Coverage (↓)
5)根据表6所有算法的Coverage值可看出:本文算法与MLNB、MDDMspc、MDDMproj、PMU、MFNMIpes这五个算法进行对比时,8个数据集中有4个数据集的Coverage值最小,即效果最好,在数据集Cal500上的Coverage值与MFNMIpes算法的值相差不超过0.8526,在数据集Reference上,MDDMspc的Coverage值相对于SFS-FMI-SW仅减小了0.0087,差距非常小.本文算法与所有算法进行对比时,算法SFS-FMI-SW的Coverage值的排序都位于前四.从平均排序中来看,SFS-FMI-SW排在第1位.
6)从图2-图3可发现:图2和图3分别为数据集Business和Science在SFS-FMI-SW算法上同 MDDMspc、MD-DMproj、PMU、MFNMIpes在5个评价指标上的分类性能对比,由图可能看出在本文SFS-FMI-SW算法上分类性能曲线的变化情况明显占优.类似的,其他数据集也可以绘制分类性能曲线,限于篇幅,略.

图2 Business数据集的各个评价指标的性能变化Fig.2 Changes in performance of various evaluation indicators of Business data set
7)根据以上实验结果分析以及算法在5个评价指标上的实验结果可知,本文算法在大部分评价指标上优于其他对比算法,特别是在评价指标Average Precision和One Error上,性能基本优于其他算法,所有算法在各评价指标的综合排位中,本文所提的算法均位列第1,这也验证了本文提出的SFS-FMI-SW算法是有效的.
4.4 算法有效性统计性假设检验
为了进一步验证本文算法的有效性,运用统计学知识,在8个数据集上,本文采用显著性水平为0.1的Friendman test[29],对于每个评价指标,我们都拒绝零假设,若两个算法在所有数据集上的平均排序的差高于临界差(critical difference,简称 CD),则认为它们有显著性差异.图4给出了所有算法在不同评价指标上的比较,根据公式(13)可计算出CD=2.9085(K=7,N=8),坐标轴画出了各种算法的平均排序,并且坐标轴上的数字越小则表示平均排序越低,线段连接则表示两种算法性能没有显著差异.

图3 Science数据集的各个评价指标的性能变化Fig.3 Changes in performance of various evaluation indicators of Science data set
(13)
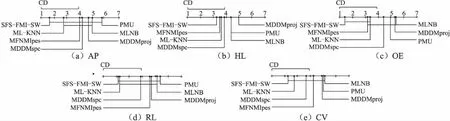
图4 使用Friendman test测试比较几种算法的性能Fig.4 Comparison of SFS-FMI-SW against other comparing algorithms with the Friendman test
从图4不难发现:在5个评价指标上,本文提出的算法SFS-FMI-SW都基本优于其他算法.
5 结 语
本文引入新的模糊信息熵,提出了结合滑动窗口机制特征选择算法,尝试解决动态或增量问题中流特征选择问题,实验结果和假设检验进一步说明本文算法是有效的.不足之处是本文算法将窗口设置为固定大小,在一定程度上影响算法的效率和性能.实际情况中,由于每个时刻产生的特征个数可能不同,窗口过小则不符合实际需求,窗口过大则使内存资源无法得到充分利用.因此,下一步将考虑根据每个时刻产生特征的个数而调整合适大小的窗口使其更符合对流特征的选择问题.
