结合空间划分和支持向量机的两级定位算法
2019-02-15李志强
周 瑞,鲁 翔,李志强,武 悦,桑 楠
(电子科技大学 信息与软件工程学院, 成都 610054)
1 引 言
定位服务给人们日常生活带来了诸多方便.卫星定位已能够满足各种室外基于位置服务的需求,而室内环境中由于卫星信号易受遮挡且存在多径效应,卫星定位系统无法提供高精度定位服务,导致室内基于位置的服务无法获得大规模应用.利用声音[1]、光[2]等信号源可以实现高精度室内定位,但其信号受环境影响较大,不具有普适性.胡等[3]融合GPS与WiFi实现室内外无缝定位模型.WiFi指纹匹配是室内定位的常用方法.WiFi指纹由若干接入点(Access Point, AP)及其信号接收强度指示(Received Signal Strength Indication, RSSI)组成.通过离线建立目标定位区域的WiFi指纹地图,采用确定性或随机性指纹匹配算法,能够实现离散或连续的位置估计.然而由于室内环境的复杂性以及WiFi信号的不稳定性,WiFi指纹定位往往不够精确,特别是大范围应用时误差较大.为提高大范围定位的精度,本文采用两级定位算法,第一级定位确定目标所在子区域,第二级定位在已确定子区域中进行精确定位.其关键在于:1) 如何划分定位空间;2) 如何进行子区域确定;3) 如何在子区域内精确定位.
空间划分的思想由Borenovic等[4]首先提出,将定位区域人工划分成固定网格.定位时首先通过人工神经网络(Artificial Neural Network, ANN)根据WiFi指纹确定子区域,然后在子区域内应用ANN确定精确位置.该方法人工固定划分空间,没有考虑WiFi信号特征,对提高定位精度贡献不明显.Vahidnia等[5]使用支持向量机(Support Vector Machines, SVM)对定位空间进行网格划分,将相似WiFi指纹划分到同一网格内.定位时首先通过SVM算法对WiFi指纹进行分类确定子区域,然后在子区域内通过ANN或贝叶斯概率模型(Bayesian Probabilistic Modeling, BPM)进行精确定位.该方法能够提高定位精度,但实验场景较小,测试点较少.Lee等[6]提出一种基于SVM和K-means的聚类算法(SVM-C)来划分信号空间.定位时首先确定聚类簇,然后在该聚类簇中采用最大似然(Maximum Likelihood, ML)或核方法估计精确位置.该方法能明显提高定位精度,但没有对离群点进行处理.为解决空间划分中的离群点问题,Mo等[7]提出一种在物理距离约束下进行信号指纹聚类的空间划分聚类(Spatial Division Clustering, SDC)方法.定位时该方法使用遗传算法和支持向量机(Genetic Algorithm and Support Vector Machine, GA-SVM)来确定子区域,然后使用加权K近邻算法(Weighted K-Nearest Neighbors, WKNN)确定精确位置.其实验未考虑房间,仅在走廊进行.
以上研究表明有效的空间划分可以提高WiFi指纹定位精度[5-7].在此基础上我们提出一种优化的基于K-means聚类的空间划分算法.空间划分后实施两级定位:第一级是粗略定位,采用SVM分类(Support Vector Classification, SVC)确定子区域;第二级是精确定位,采用SVM回归(Support Vector Regression, SVR)确定精确位置坐标.在室内包括走廊和多个房间的较大范围实验中,获得的子区域分类正确率为95.42%,平均定位误差2.51米.本文主要贡献包括:
1) 提出优化K-means聚类的空间划分算法,该算法考虑到WiFi信号的相似性和物理位置的邻近性,能去除聚类产生的离群点,并寻找最优聚类模型,实现最优空间划分;
2) 提出采用SVM分类和回归相结合的两级定位,一级定位采用SVM分类确定子区域,二级定位采用SVM回归在子区域内进行精确定位,每个子区域建立各自专有的SVM回归模型,能更精确地描述本子区域中信号和位置之间的关系;
3) 实验证明提出的空间划分算法优于现有空间划分算法(平面图划分法和SVM-C算法);
4) 实验证明提出的基于SVM分类和回归的两级定位算法优于常用单级定位算法.
2 基于空间划分的两级定位
2.1 基本算法
基于空间划分的两级定位的基本流程如图1所示,包括训练阶段和定位阶段.训练 阶段采集每个参考位置点的WiFi指纹,采用优化K-means聚类空间划分算法,根据WiFi指纹相似性和参考点邻近性对参考点进行聚类,每一个聚类簇形成一个子区域,从而将大的定位区域划分成若干小的子区域,完成空间划分.根据WiFi指纹及其对应的子区域标签,训练并建立子区域SVC分类模型,用于两级定位中的第一级,即确定目标所在子区域.根据每个子区域内采集的WiFi指纹及其采样位置坐标,针对每个子区域建立各自的SVR回归模型,用于两级定位中的第2级,即精确计算目标的位置坐标.定位阶段分别采用SVM分类和回归来实现两级定位.第1级定位根据在线测得的WiFi指纹,利用训练阶段建立的子区域SVC分类模型确定目标所在子区域,第2级定位通过对应子区域的SVR回归模型计算出目标的精确位置坐标.

图1 基于空间划分的两级定位Fig.1 Two-layer localization based on space partitioning
2.2 优化K-means聚类的空间划分算法
空间划分可以简单地根据室内平面图进行,但该方法不够灵活,特别是在大型开放的室内空间或缺少平面图的情况下,不能有效划分空间区域.在局部邻近的物理空间采集的WiFi指纹,通常在信号空间也相似.根据该原理,可以通过各参考点的信号特征相似度来划分目标区域.K-means聚类[8,9]是一种无监督学习算法,能够对参考位置点的WiFi指纹进行聚类,并将聚类结果作为子区域划分的依据.本文提出优化的基于K-means聚类的空间划分算法,包括三部分:
1) 由于在每个参考位置点会采集多个WiFi指纹,因此首先计算每个参考位置点的WiFi指纹均值,然后根据WiFi指纹均值对这些参考位置点进行K-means聚类,分成K个聚类簇,作为空间划分的初步结果,K是预定义的聚类簇数;
2) 采用K-means算法在指纹信号空间聚类往往产生离群点,即一个本应属于聚类簇i的点p被划分到另一个聚类簇j中,因此需要对离群点进行处理,将其标记到正确的聚类簇中,即划分到正确子区域中;
3) 提出并定义空间划分评估函数,采用该函数评估每次空间划分的结果,经过多次迭代后得到最优空间划分.
2.2.1 基于K-means聚类的空间划分

(1)
其中l表示信号指纹的维度,即AP的数量.通过K-means聚类进行空间划分就是解决以下问题[8,9]:
(2)



(3)
在M步,固定γik,最小化公式(2)中的J,得到:
(4)
M步中得到的μk(k=1,2,…,K)作为新的聚类簇中心代入到E步中,迭代,直到J收敛.
2.2.2 离群点处理
采用K-means聚类算法对参考位置点的信号指纹均值聚类后,结果中存在离群点.例如图2所示,聚类结果显示位置点q被划分到较远的子区域Q里,而实际上该点在空间划分后应属于子区域P,那么参考位置点q就是离群点.离群点是空间划分中的错误点,需要对它们进行重新标定,以获得合理的空间划分结果.对离群点的处理需要首先找到离群点,然后重新标定它们所属的子区域.
1) 离群点识别:比较每个参考位置点和其邻近的参考位置点所属子区域.例如某一参考位置点所属的子区域为d,其邻近的参考位置点所属的子区域分别为{d1,d2,…,dm},m为邻近参考点的数量.若所有邻近参考位置点所属子区域与该参考点不同,即∀i,di≠d,则该参考点为离群点.

图2 离群点处理Fig.2 Outlier removal
2) 离群点重标定:找出该离群点的邻近参考点极大子区域,假设为dmax,将该离群点所在子区域重标定为dmax.
如图2,三角形q为一个参考位置点,聚类后其所属子区域为Q,而q的4个邻居参考点{p1,p2,p3,p4}都被划分到同一个子区域P,q是离群点,它会被重新划分到P子区域.
2.2.3 聚类模型寻优
由于K-means聚类算法的初始簇中心是随机的,导致每次聚类的结果不同,空间划分结果也不相同.为获得最优空间划分结果,本文提出并定义空间划分评估函数来评估每次K-means聚类的优劣,迭代若干次后,寻找出最优聚类结果,即最佳空间划分.空间划分评估函数f定义为:
(5)
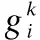
2.3 基于SVM的两级定位
空间划分后,实际定位采用两级定位方式.首先通过SVM[8,9]分类确定子区域,然后在该在区域内进行SVM回归获得精确位置.相对于针对整个定位区域的统一的回归模型,针对每个子区域建立专有回归模型能更加精确地表达子区域中信号指纹和位置之间的关系,因此更适合精确定位.
2.3.1 基于SVC的子区域确定
子区域确定采用分类方式,因此需要在训练阶段建立子区域分类模型.假设整个定位区域的AP集合为A={a1,a2,…,al},l为AP数量,子区域集合为D={d1,d2,…,dK},K表示子区域数目,一个子区域di中的AP集合可表示为Ai={ai1,ai2,…,aim}⊆A,m≤l,一个WiFi指纹样本可表示为(di,(xi,xj),ri),其中di∈D表示样本采集位置所在的子区域,ri=(ri1,ri2,…,rij,…,rim)表示采集的信号指纹,rij表示AP集合Ai中第j个AP的RSSI值,j≤m≤l,(xi,xj)为样本采样位置的物理坐标.
训练阶段,采集定位区域中所有参考位置点的WiFi信号指纹并记录其物理位置坐标.整个定位区域经过空间划分后,分为若干各子区域,同时所有的WiFi指纹会被标记上其所属的子区域.这时的WiFi指纹样本集可以表示为{(di,ri)|i=1,2,…,n},n为样本数量.对于每个子区域的样本,可分为两种类型:一类是样本采集区域属于该子区域的样本,标记为+1;另一类则是样本采集区域不属于该子区域的样本,标记为-1.这样,针对每一个子区域的训练样本集可表示为{(ci,ri)|i=1,2,…,n},ci∈{-1,+1}.使用该样本集,就可以训练每个子区域的SVC分类器.
第一级定位时,根据实时采集的WiFi信号指纹,由子区域SVC分类器判定属于哪个子区域.假设r∈Rl代表一个实时信号指纹,将其提交给所有子区域SVC分类器,如果c=+1,则r属于该子区域,否则不属于该子区域.
2.3.2 基于SVR的精确定位
精确定位需要确定目标的位置坐标,可以作为连续问题通过回归来解决.本文通过SVR建立每个子区域中位置坐标与WiFi信号指纹之间的依赖关系,进行每个子区域中的精确定位.SVR建模的目标就是确定函数fx和fy,分别描述信号指纹r与位置坐标x和y之间的依赖关系.训练每个子区域各自的SVR回归模型时,只需要使用各子区域中的信号指纹样本集{(dk,(xi,xj),ri|i=1,2,…,nk},其中dk代表子区域k,nk代表该子区域的训练样本数量.WiFi信号指纹r与位置坐标x分量之间的函数关系fx使用样本集{(dk,xi,ri)|i=1,2,…,nk}进行建模,而信号指纹r与位置坐标y之间的依赖关系fv使用样本集{(dk,yi,ri)|i=1,2,…,nk}进行建模.精确定位时,将实时信号指纹r提交给所属子区域d的x轴回归模型fx得到目标位置的坐标x分量,同时指纹r代入所属子区域的y轴回归模型fy得到坐标y分量,获得目标的精确位置(x,y).
3 实 验
实验环境为学校第三教学楼的二楼整层,包括多个房间和走廊,定位区域为64m×16m.实验采用校园无线网中已经安装部署的AP,没有额外增加AP.实验步骤分为数据采集、空间划分、分类和回归模型训练、两级定位四部分.数据采集阶段,借助于采集软件,实验者采集并记录每个参考位置点的WiFi指纹信息及其位置坐标.参考位置点共计200个,每个参考位置点采样32次,对应4个不同方向,采样率为1Hz.用同样的方法采集240个测试位置点的信号指纹,每个测试位置点采样3次,其均值作为测试样本.参考位置点和测试位置点的详细分布如图3(a)和图3(b)所示.训练数据和测试数据的采集分别在不同时段进行,分两天完成,总计花费约4小时.空间划分阶段,采用提出的优化K-means聚类的空间划分方法对图3(a)所示的参考位置点的训练样本进行聚类和空间划分,形成若干子区域.模型训练阶段,分别建立基于SVC的子区域分类模型和针对每个子区域的基于SVR的回归模型.实时定位阶段,通过训练的的分类和回归模型,根据实时WiFi信号指纹,分类确定子区域并在子区域内回归确定精确位置坐标.

图3 实验环境Fig.3 Experimental environment
3.1 空间划分结果
为了说明本文提出的空间划分方法的有效性,比较了本文提出的优化K-means聚类的空间划分方法和其它空间划分方法,即基于平面图和基于SMV-C聚类的空间划分.
室内环境中,墙体是天然的空间边界,WiFi信号穿透它们时会有显著衰减.通常同一房间内的信号特征具有较强相似性,而不同房间的信号特征相似性较弱.因此可根据室内建筑结构将室内空间划分成多个子区域,如一个房间或者一段走廊代表一个子区域.这种空间划分可根据室内平面图来进行.该方法简单有效,但是精确的平面图不易获得,导致无法进行划分,另外对于室内较大面积的连通区域,由于缺少墙体等天然边界,也无法进行有效空间划分.图4(a)是采用基于平面图的空间划分方法对实验环境的空间划分:整个定位区域被划分为15个子区域,编号1-5和12-15按房间分为9个子区域,编号6-11按走廊分为6个子区域.
使用本文提出的优化K-means聚类的空间划分结果如图4(b)所示.8个聚类簇在经过信号聚类、离散点处理和模型寻优后得出.聚类结果根据WiFi信号相似性和物理位置邻近性共同决定.聚类结果将整个定位区域划分为8个子区域.在一定程度上,优化K-means聚类的空间划分结果和基于平面图的空间划分有些相似,但在门附近和走廊区域有些不同,房间和相邻走廊常被划分到同一个子区域.这是由于这些区域的信号相似性决定的.
作为比较,我们实现了基于SVM-C聚类的空间划分方法[6].该方法本质上是一种改进的K-means聚类算法,但两点之间的距离采用的是两点各自指纹空间上的SVM超平面之间的距离,距离越小表示相似度越高.采用同一套数据集,基于SVM-C聚类的空间划分结果如图4(c)所示.在一定程度上,该划分结果和平面图也有相似之处,但是该算法有合并房间为同一子区域的情况,导致整个空间划分不均衡.

图4 空间划分结果Fig.4 Results of space partitioning
3.2 定位结果
空间划分后分别建立SVC子区域分类模型和每个子区域的SVR回归模型.由于存在多个子区域,子区域确定是多分类问题,本文采用一对一方法来解决[10].如果有K个子区域,则需要训练K(K-1)/2个SVC模型,因此本实验中优化K-means聚类的空间划分和基于SVM-C聚类的空间划分各需要28个SVC模型,而基于平面图的空间划分则需要105个SVC模型.由于位置是二维坐标,需要2K个SVR回归模型,因此优化K-means聚类和SVM-C聚类各需要16个SVR回归模型,而平面图法则需要30个SVR回归模型.SVM算法的实现采用libSVM1,核函数选择径向基函数(Radical Basis Function, RBF),SVC算法采用C-SVC[8,9],SVR算法采用v-SVR[11].
3.2.1 子区域确定
对于提到的3种空间划分方法,对其子区域确定和精确定位结果做了对比.评估标准包括子区域分类正确率、平均定位误差和累计定位误差分布.具体结果见表1.采用本文提出的优化K-means聚类的空间划分的子区域分类正确率达到96.67%(240个测试点中有8个分类错误);使用基于SVM-C聚类的空间划分的子区域分类正确率为92.92%,有17个测试点分类错误;而基于平面图的空间划分的分类正确率为94.85%,有13个测试点分类错误.从分类效果来看,本文提出的优化K-means聚类的空间划分算法最优.详细分类结果如图5所示,小圆圈代表正确分类的测试点,叉叉为错误分类的测试点.

图5 子区域确定结果Fig.5 Results of subregion determination
3.2.2 精确定位
在子区域确定的基础上,在子区域内进行位置坐标(x,y)的确定,即精确定位.本文比较了三种空间划分方法在经过两级定位后的平均误差和累计误差分布.优化K-means聚类的空间划分的两级定位的平均误差为2.51米,相比基于SVM-C聚类的空间划分的两级定位误差3.02米,精度提高了16.9%,相比平面图法的两级定位误差2.58米,精度提高了2.7%.详细定位结果如图6所示,三张图中,箭头尾部为目标实际位置,箭头头部指向估计位置.从最终定位结果看,优化K-means聚类的空间划分优于基于SVM-C聚类的空间划分和基于平面图的空间划分.两级定位的平均定位误差和定位误差累积分布显示在表1中.

图6 基于空间划分的两级定位结果Fig.6 Two-layer localization based on space partitioning
3.2.3 两级定位与单级定位
我们将提出的基于空间划分和SVC-SVR的两级定位和多种主流单级定位算法进行比较,包括SVR,近邻算法(Nearest Neighbor, NN)和K近邻算法(K- Nearest Neighbor, KNN).比较结果列在表2中.从表中可以看出,两级SVC-SVR算法平均定位误差最小,为2.51米,明显优于单级的SVR(3米)、NN(3.93米)和K=4时的KNN(3.57米).四种算法的累计误差分布也显示在表2中,两级SVC-SVR定位算法精度最高,累积定位误差小于1米的百分比为14.58%,小于2米的为40%,小于3米70%,小于4米85.42%,小于5米94.59%,明显优于SVR、NN和KNN.
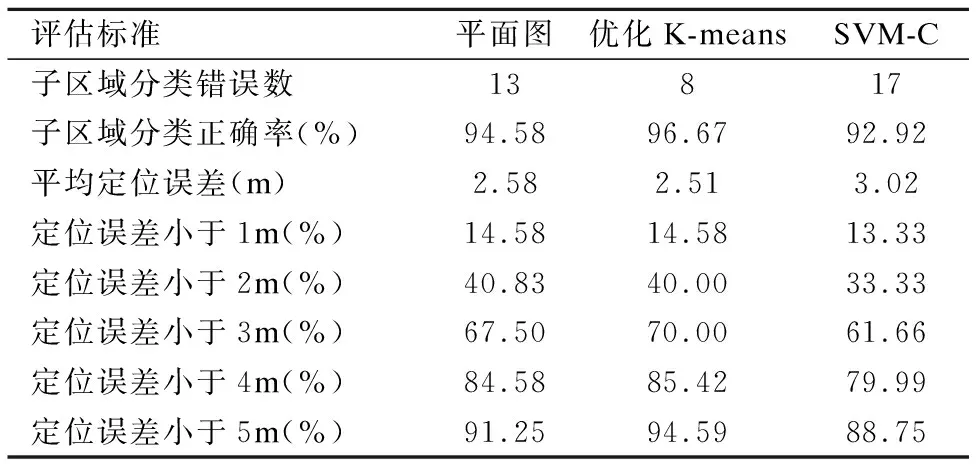
表1 SVM子区域确定和定位结果Table 1 Subregion determination and localization with SVM

表2 SVC-SVR,SVR,NN和KNN定位精度对比Table 2 Comparison of SVC-SVR, SVR, NN and KNN
4 结束语
本文提出了一种基于空间划分和支持向量机的两级室内WiFi指纹定位算法,包括3部分:
1) 提出一种优化的基于K-means聚类的空间划分方法,在考虑空间特征和信号特征的情况下,对定位区域进行空间划分产生子区域;
2) 采用SVM分类进行一级定位,确定目标所在子区域;
3) 提出采用SVR回归进行二级定位,在子区域内进行精确定位.
实验结果表明,由于空间划分后针对每个子区域建立的回归模型能够更加精确地反映该区域内的信号特征,因此两级定位算法的定位性能明显优于单级定位;本文提出的空间划分方法同时兼顾信号特征和物理空间特征,因此定位效果优于其它空间划分方法.在包含多个房间和走廊的较大实际环境进行的实验中,本算法达到96.67%的子区域分类正确率和2.51米的平均定位精度.
