陶瓷基FGM材料线形变厚度圆板的热后屈曲
2019-02-15李清禄段鹏飞张靖华
李清禄, 段鹏飞, 张靖华
(兰州理工大学 理学院,兰州 730050)
功能梯度材料(functionally graded material,FGM)最早是由日本科学家为航空航天结构元件能够适应高温梯度环境而提出的。FGM材料通常是由一个表面的纯陶瓷按照成分多少连续梯度变化到另一个表面的一种新型复合材料。这种梯度的变化具有抵抗高温梯度、减小应力集中等优点。FGM结构的出现立刻吸引了学者们的关注,成为航空航天等领域的研究热点[1-3]。
Liviu等[4]研究了FGM梁处于高温环境中的振动和屈曲问题,得出温度对FGM梁的屈曲特性与振动的频率有不同程度的影响。Najafizadeh和Eslami[5]研究了轴对称FGM圆板受到面内径向压力和热载荷作用下的屈曲和稳定性问题,并给出了问题的解析解,分析了不同径向压力和热载荷下的屈曲临界载荷。Ma和Wang[6]详细研究了FGM圆板在机械和热载荷下的弯曲和屈曲力学响应,并给出了圆板弯曲的中心挠度及屈曲特性曲线。Shen[7]利用双参数摄动方法研究了压电FGM剪切板在热环境中的后屈曲行为,并对比分析了热-电作用的FGM板屈曲临界载荷。Zhang[8]考虑了材料的温度相关性,和双参数弹性地基FGM椭圆板的非线性弯曲行为以及不同参数地基对FGM椭圆板中心挠度的影响。宋健和温卫东[9]采用实验的方法研究了树脂基复合材料在不同温度环境下的拉伸及面内剪切力学性能,分析了温度变化对材料的弹性模量、强度的影响规律,并提出了预测力学模型。张坤等[10]采用双道次热压缩实验,研究了温度对新型复合材料力学行为的影响。
以上研究都是等厚度圆板的力学行为,由于制造技术和材料科学的发展,人们能将圆板加工成各种变厚度的圆板以满足航空航天工程领域的要求,目的是通过改变几何尺寸和减轻自重。尤其FGM材料应用在航空技术的兴起,变厚度FGM结构力学行为的研究具有现实的工程背景。周续等[11]以航空发动机机匣为对象,研究了材料切除对机匣铣削动力学与稳定性的影响。王云[12]用DQ法研究了变厚度Mindlin圆形板的轴对称弯曲问题,为工程结构优化提供了依据。文献[13]分析了径向梯度功能材料变厚度弹性地基扇形板的稳定性问题,分析了厚度变化对扇形板屈曲临界载荷的影响。Efraim和Eisenberger[14]研究了均匀变厚度环板和FGM环板的振动特性,并对比分析了梯度指数、厚度变化系数对环板振动无量纲频率的影响。
总的来看,功能梯度材料变厚度圆板的静动态响应方面的研究十分有限,尤其在热环境中的稳定性及振动力学特性鲜有涉足。本工作基于哈密顿原理,建立陶瓷基FGM弹性薄圆板在热环境中的后屈曲控制微分方程,采用打靶法研究不同厚度变化系数以及不同陶瓷基成分含量下FGM圆板的后屈曲力学行为,详细分析厚度变化系数,陶瓷基梯度指标对圆板屈曲载荷以及后屈曲行为的影响。
1 力学分析模型
考虑一个半径为R,沿径向方向线形变厚度变化的复合材料圆板。径向位移分量为u 。坐标系统 (r,θ,z)置于圆板几何中面上,设r为径向且由板中心向外为正,θ为环向,z坐标垂直于中面,如图1所示。假设圆板厚度从板中心到外边界按式(1)所示线形变化:
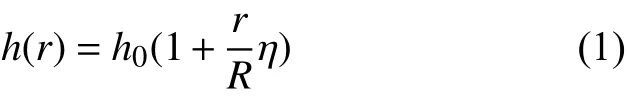
式中:h0为板中心处的厚度;η为厚度变化系数。

图1 变厚度陶瓷基-FGM圆板Fig.1 Ceramic based-FGM circular plate with variable thickness
1.1 陶瓷基FGM材料物性参数描述
考虑FGM圆板为陶瓷基复合材料板,板的下面为纯陶瓷(ZrO2),陶瓷材料的体积分数可用下面的表达式给出
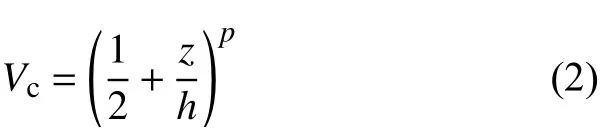
式中:h为圆板的厚度;p为非负实数;p代表陶瓷基功能梯度材料从上表面过渡到下表面的梯度指标。p=0代表纯陶瓷材料,随着p的增加,板内陶瓷材料的成分逐渐减少,直到变成纯金属。
采用Voigt等应变线性混合率模型,FGM材料的等效物性参数弹性模量E、热膨胀系数α和热传导率K描述为
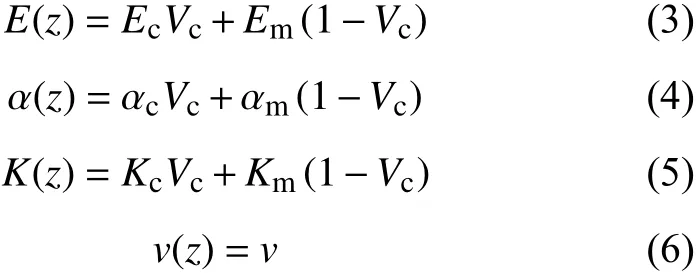
式中:m和c分别代表金属和陶瓷的成分;Em,Ec为金属和陶瓷的弹性模量;αm,αc为金属和陶瓷的热膨胀系数;Km,Kc为金属和陶瓷的热导率;Vm,Vc为金属和陶瓷的体积分数;v为材料泊松比。
1.2 温度场描述
陶瓷一侧和金属一侧的温度分别记为Tc和Tm,且两侧温度都均匀分布,板内温度沿厚度变化,基础温度为T0= 300 K。其中升温满足一维热传导方程

边界条件为:
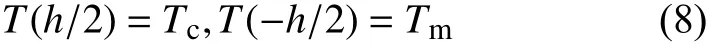
式(7)在边界条件(8)下的幂级数形式的解为
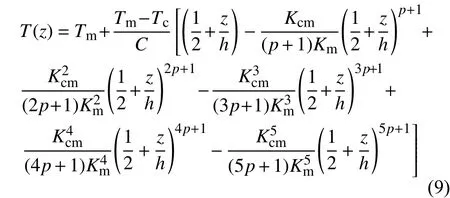
其中

2 控制微分方程
经典板理论所基于的位移场为:
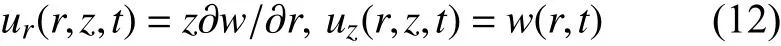
式中:w为z方向的位移;t代表时间。
薄膜力和弯矩可表述为
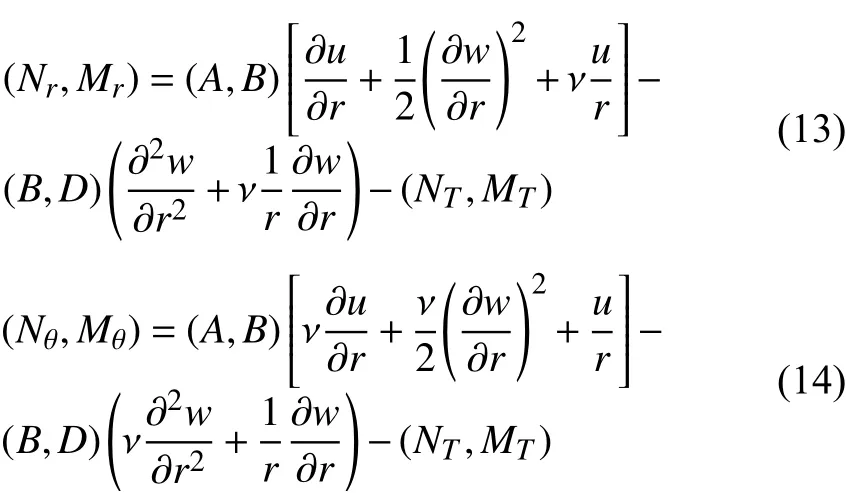
其中,刚度系数以及热薄膜力和热弯矩为
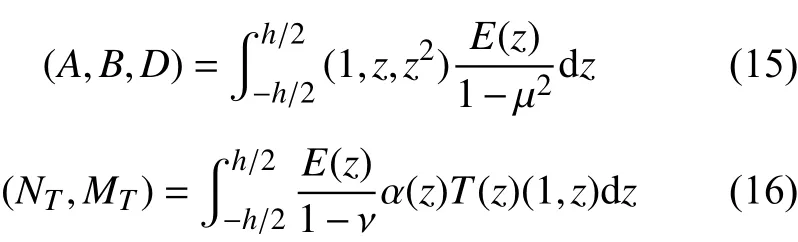
将式(3)代入式(15),(16),通过积分得到

φi(i=1,2,3,4,5)为无量纲系数。应变能变分:
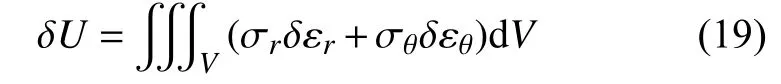
式(19)中, εr,εθ和 σr,σθ分别为径向和环向的应变和应力。动能变分:
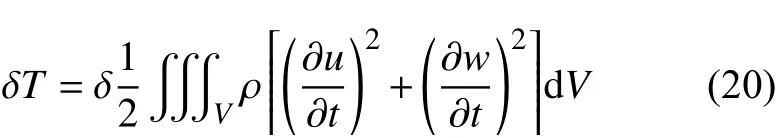
Hamilton原理:
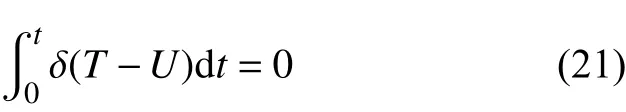
将方程(19),(20)代入方程(21),再利用式(13),(14),并令各量与时间无关,可得到如下无量纲形式的控制方程,即功能梯度圆板的静态平衡方程。
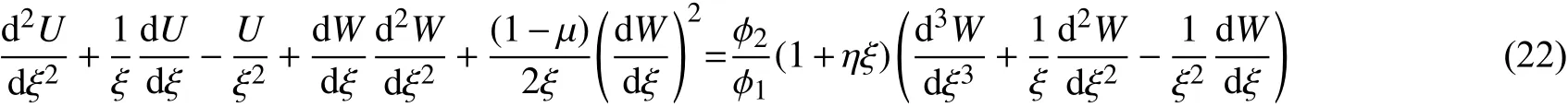
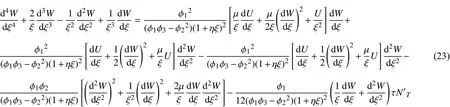
上述方程的无量纲形式如下

考虑周边夹紧圆板,其边界条件描述为
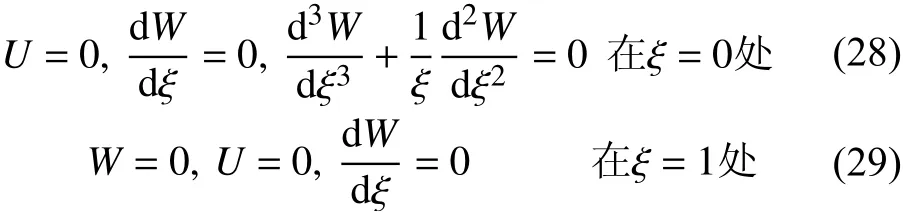
图2给出了基础温度Tc= 300 K,Tm= 300 K时变厚度板中心挠度W(0)与无量纲热载荷τ之间的特征关系曲线。由图2可以看出,在给定梯度指标p下,随热载荷的增加,变厚度中心挠度非线性增加,随着梯度指标的增大,板的临界载荷增大,说
3 数值模拟及讨论
由于打靶法在求解两点边值问题中计算精度高和收敛快,所以这里选择打靶法求该问题的数值解,打靶法的具体求解可参看文献[15]。计算中,陶瓷材料和金属材料的物性参数,即弹性模量、泊松比、热膨胀系数、导热系数分别为
陶瓷(ZrO2): Ec=132.2 GPa, νc=0.31,αc=13.3×10-6K-1,Kc=1.78 W/m·K,
金属(Ti-6Al-4V): Em=122.7 GPa, νm=0.2882,αc=7.43×10-6K-1,Kc=6.10 W/m·K明FGM板具有更大的稳定性,同时也可以通过调节陶瓷基成分的含量来改变圆板的临界载荷。
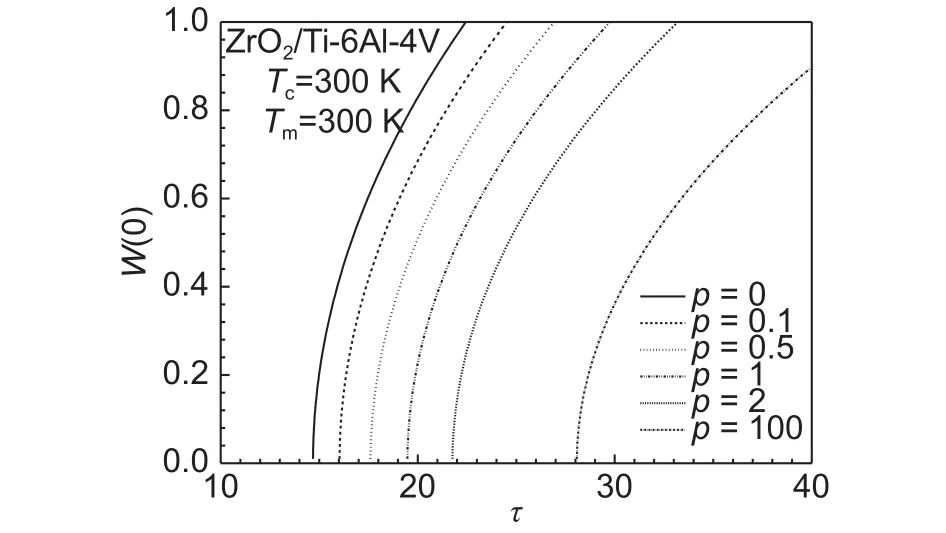
图2 W(0)-τ 关系曲线Fig.2 Relationship curves of τ and W(0)
图3 给出了陶瓷基FGM圆板的梯度指标为p = 0.1时,不同厚度变化系数η下,均匀升温场中的平衡路径特性曲线。不难看出,在相同梯度指标下,板的厚度变化对临界载荷并没有影响,但是过屈曲后平衡路径是不同的,随着η的增加,中心挠度增加。
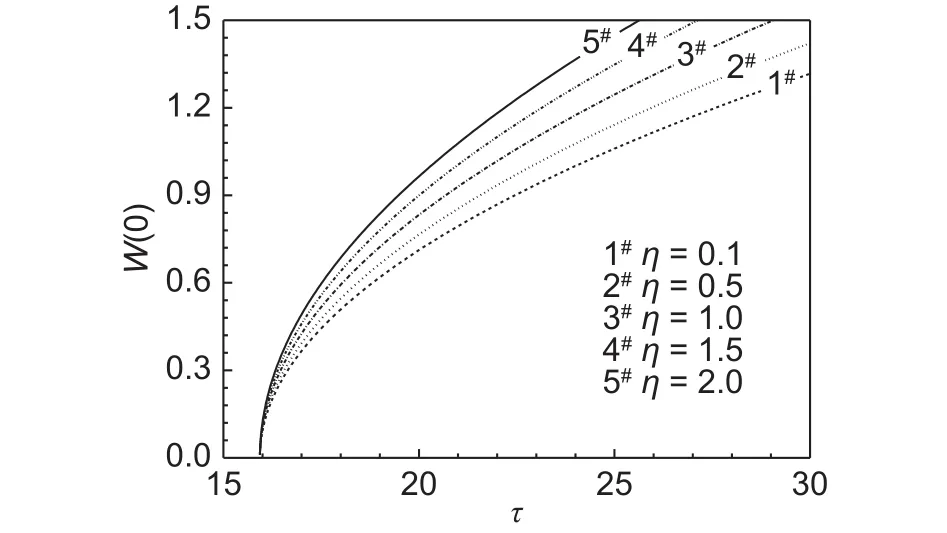
图3 不同厚度变化系数下W(0)-z关系曲线Fig.3 Relationship curves of z and W(0) for different η
图4 为均匀升温和非均匀升温Tr= 2时,板中心挠度与无量纲热载荷τ之间的特征关系曲线。通过比较看出,纯陶瓷材料和陶瓷基功能材料在非均匀升温下的临界热载荷小于均匀升温下的临界热载荷。
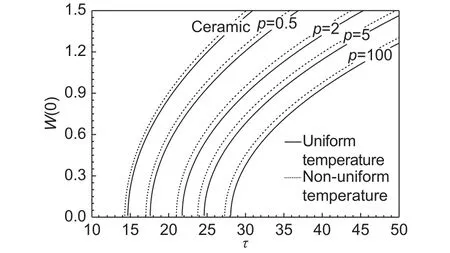
图4 均匀升温和非均匀升温下板中心挠度和热载荷的比较Fig.4 Comparison of central deflection and thermal load of plates under uniform heating and non-uniform heating
由图4可知,板的临界热载荷并不取决于厚度变化系数,主要取决于板中心的厚径比,即圆板厚度和半径的比值,过屈曲路径曲线与横坐标的交点即为板的屈曲临界热载荷,可以看出在厚度变化系数分别取0.1,0.5,1,1.5,2时,与横坐标的交点不变,因此圆板的屈曲临界载荷主要取决于板中心的厚径比。表1给出了不同板中心厚径比δ下,不同指标p时,圆板的屈曲临界温度参数,其定义为
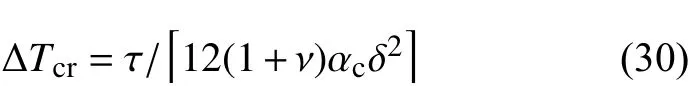
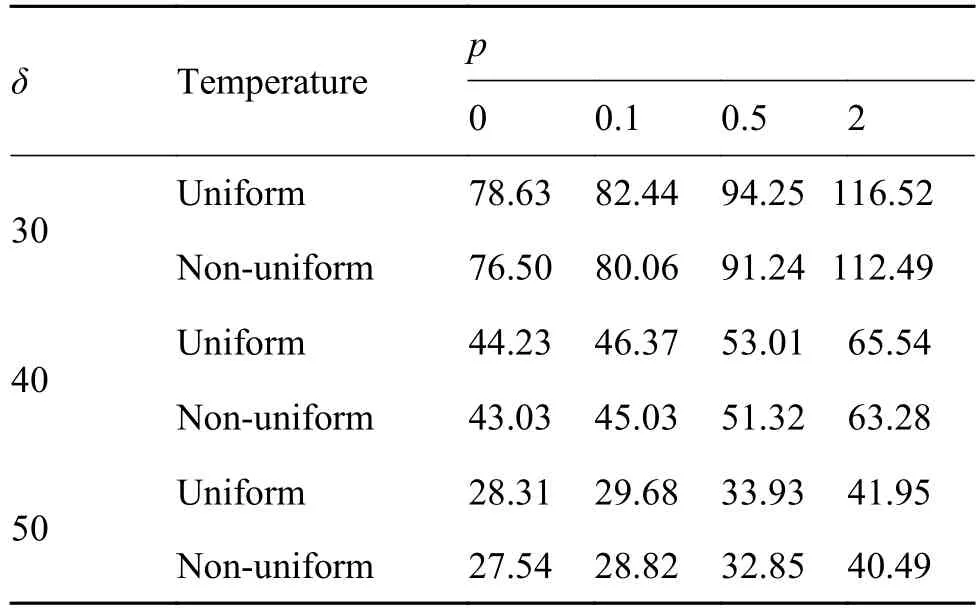
表1 不同 δ 下FGM圆板临界温度参数Table1 Values of critical temperature parameter with different δ
可以看出,给定中心厚径比时,板的临界温度随梯度指标的增加而增加,在一定的梯度指标下,板的临界温度随中心厚径比的增加而减小,即板线形变化的斜率越大相应的临界温度越高。
图5为不同上下表面升温比下,即非均匀升温下的热临界载荷与最大挠度之间的关系。显然,上下表面升温比越大,热临界载荷会随之降低。同样的热载荷下,变形越大。
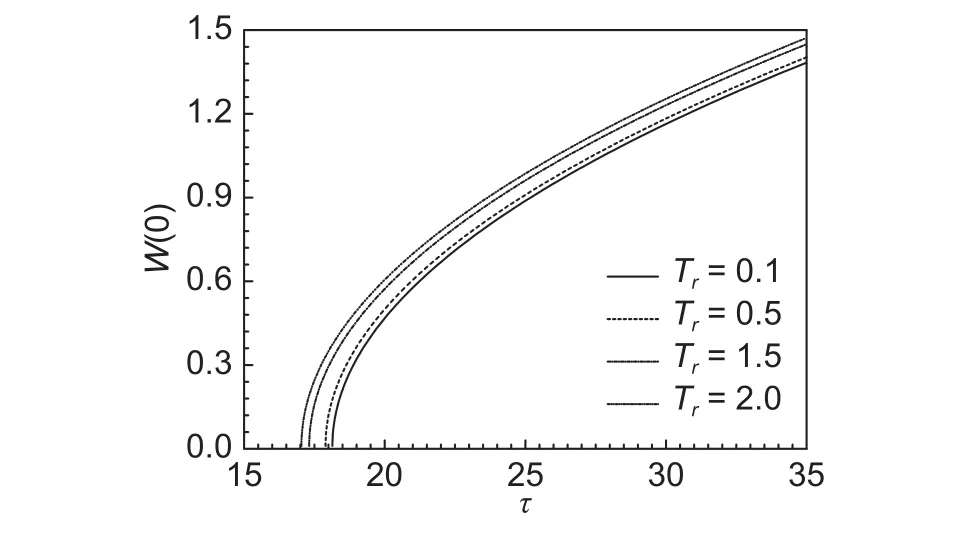
图5 不同Tr下的W(0)-τ (p = 0.5,η = 0.2)Fig.5 Relationship curves of τ and W(0) for different Tr(p = 0.5, η = 0.2)
图6 为p = 0.1,上下表面升温Tr= 1情况下,不同截面变化系数η下FGM圆板的后屈曲构形图。显然,η的不同取值对板的变形有很大影响。η越大,即板中心厚度和外边厚度变化的斜率越大,板的变形越大。图7为p = 0.5,截面变化系数η = 0.2,τ = 30情况下,上下表面升温Tr取不同值时,陶瓷基圆板的后屈曲平衡路径构形图。可以看出,随升温比的增加,板的变形增加,且非均匀升温时板产生的挠度大于均匀升温时的。
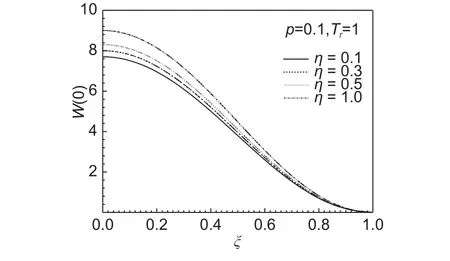
图6 不同 η 下FGM板的构形(τ = 20)Fig.6 Configurations of FGM plate for different values of η(τ = 20)
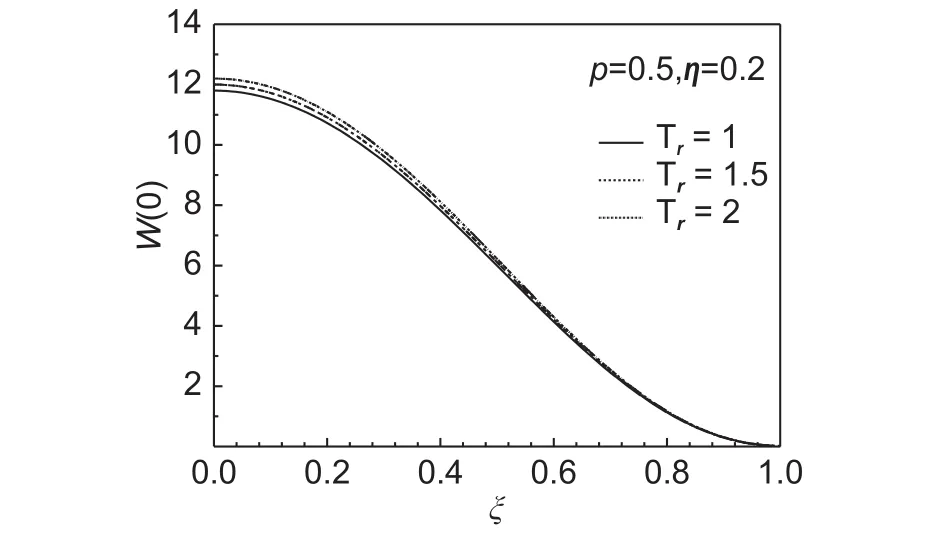
图7 不同Tr下FGM板的构形(τ = 30)Fig.7 Configurations of FGM plate for different values of Tr(τ = 30)
4 结论
(1)当厚度变化系数η为零时,即等厚度的陶瓷基圆板在基础温度场中,随着梯度指标p的增加,热屈曲载荷增加,板的变形减小。说明随陶瓷成分的减少,板具有更大的稳定性。
(2)变厚度斜率的改变并不会影响热临界载荷的值,但会影响到屈曲以后的平衡路径,随着η的增加,中心挠度也增加。
(3)陶瓷基FGM材料在非均匀升温下的临界热载荷小于均匀升温下的值,板的临界温度随中心厚径比的增加而减小,陶瓷表面和金属表面非均匀升温比越大,热临界载荷反而越小。
(4)厚度变化系数和上下表面升温比对陶瓷基F GM圆板的后屈曲特性有重要影响。
