车用永磁缓速器磁-热耦合建模与试验研究∗
2019-02-15叶乐志刘玉朋李德胜
叶乐志,刘玉朋,李德胜
(北京工业大学机械工程与应用电子技术学院,北京 100124)
前言
随着我国道路交通状况的改善和车辆通行能力的提高,重载货车高速、超载、持续制动发热等问题严重威胁着行车安全,因此,除车辆本身主制动系统外,加装辅助制动装置已成为交通安全的迫切需要[1-2]。永磁缓速器是一种基于永磁体涡流制动原理的无摩擦辅助制动装置,具有结构简单、体积小、质量轻和基本不消耗电能等优点,具有广阔的推广应用前景[3-4]。
永磁缓速器将车辆的动能或势能转换为热能,工作时产生的大量热能引起缓速器涡流盘温度急剧升高,最高可达500℃以上。涡流盘高温一方面会带来缓速器制动力矩衰退、永磁体易失磁等问题,另一方面会引起材料电磁特性特别是电导率和磁导率的非线性变化,对电磁场和温度场模型等理论计算带来较大误差。近年来国内外学者对涡流制动装置的电磁场建模、温度场建模、结构优化设计和制动性能实验等方面进行了深入研究[5-10]。尽管少数研究者认识到温度对永磁缓速器制动性能的影响不可忽略,并进行了耦合计算[11-13],但采用双向耦合方法对缓速器电-磁-热-流等多物理场耦合计算的研究较少。
本文中提出一种制动力矩可无级调节的永磁缓速器,建立缓速器电磁场和温度场模型,分析电磁场和温度场分布,得到制动特性曲线。提出一种磁-热双向耦合方法建立缓速器磁-热耦合分析模型,研究考虑温度影响的缓速器制动力矩特性,并试制缓速器样机,进行了试验研究。该项研究为缓速器优化设计提供理论支持,可用于解决永磁缓速器长时间制动产生高温导致制动力矩衰退和永磁体失磁等问题。
1 结构与工作原理
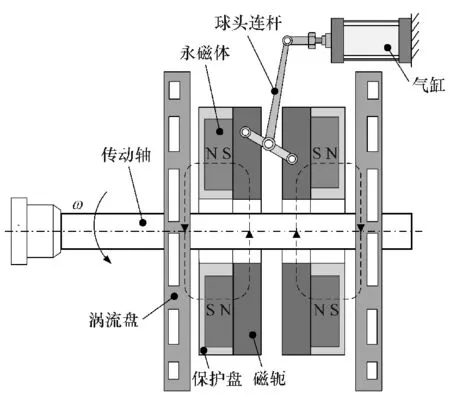
图1 永磁缓速器结构示意图
本文中提出一种新型盘式永磁缓速器,其结构如图1所示,主要由2个永磁盘、2个涡流盘和1个力矩调节机构组成,永磁盘包括永磁体、保护盘和磁轭,永磁体采用钕铁硼材料,以N,S极交替放置通过保护盘固定在磁轭上(为清晰表示,图中保护盘作透明处理)。涡流盘位于永磁盘两侧,通过法兰与车辆传动轴和变速器输出轴相连接,其上设有散热风道,采用强制风冷方式进行散热。当涡流盘靠近永磁盘时,永磁体、磁轭、涡流盘和两盘之间的气隙形成闭合磁路,涡流盘随输出轴旋转时切割永磁体产生的磁力线,感应涡流产生的磁场与原磁场相互作用,从而产生制动力矩;当涡流盘远离永磁盘时,制动减小直至解除。制动力矩调节机构由气缸和球头连杆组成,气缸固定在车架上,球头连杆与磁轭相连接,基于杠杆原理,通过控制气缸的轴向运动调节气隙大小,改变气隙磁阻和感应涡流磁场强度,从而实现缓速器的开关和对制动力矩进行无级调节。
2 电磁场数值分析
2.1 电磁场数学模型
在永磁缓速器电磁场模型中,忽略涡流盘中的位移电流,麦克斯韦方程组可表示为

式中:H为磁场强度,A/m;J为电流密度,A/m2;E为电场强度,V/m;B为磁通密度,T。
对于包含运动导体的涡流问题,其场域及边界如图2所示。设定三维涡流场的求解区域Ω,包括Ω1和Ω2,其中Ω1为涡流区域,不含源电流,Ω2为非涡流区域;Γ12为Ω1和Ω2的内部交界面;Ω的外边界有ΓB和ΓH两种定义,在ΓB上给定磁感应强度的法向分量,在ΓH上给定磁场强度的切向分量。
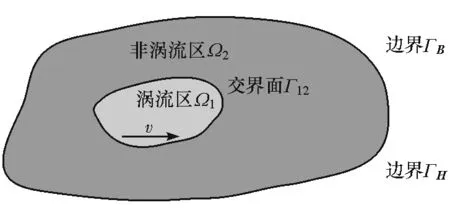
图2 运动导体涡流场域及边界
为提高电磁场数值计算的效率,引入磁矢势A和标量电位 φ,则 Ω1和 Ω2区域的控制方程[14]分别为
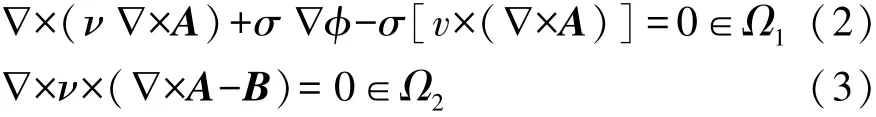
式中:ν为磁阻率(磁导率μ的倒数),m/H;σ为涡流盘电导率,S/m;v为涡流盘运动速度,m/s。根据以上方程可分别求解磁通密度B和电流密度J。
2.2 电磁场数值模型
永磁缓速器在工作时,永磁体使旋转的涡流盘内表面感应产生涡流,而涡流产生的磁动势会对气隙磁场产生增强或减弱的影响,因此气隙磁场由永磁体磁动势和涡流磁动势的合成磁动势所决定。利用展开方法对永磁缓速器进行建模分析,涡流计算模型如图3所示。各部件结构参数如表1所示。
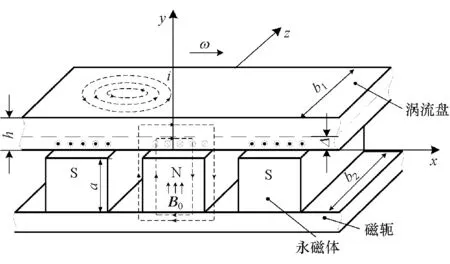
图3 缓速器涡流计算模型
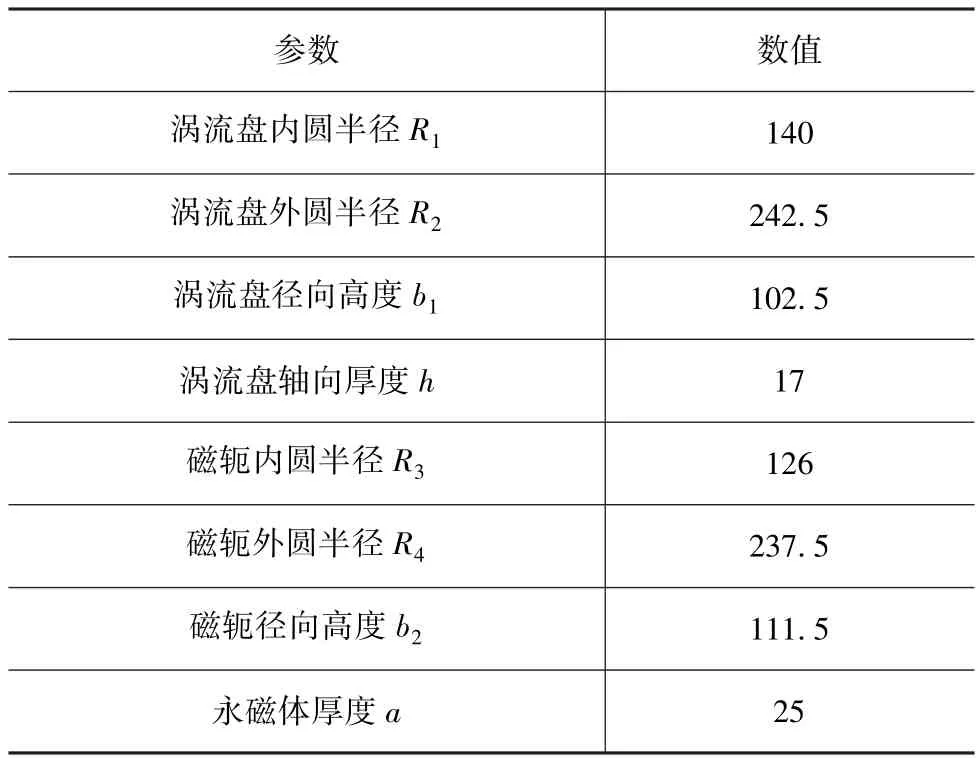
表1 缓速器模型结构参数表 mm
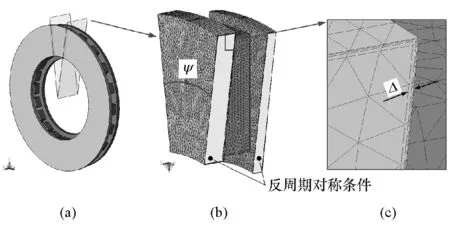
图4 电磁场计算模型及1/20网格划分模型
根据表1中的结构参数建立缓速器的电磁场数值计算模型,对涡流盘上的散热风道进行结构简化,三维模型如图4(a)所示。因保护盘不导磁,故在图3、表1和图4中皆予略去。由于模型具有周期性,为缩小计算区域和缩短计算时间,设置反对称周期对称条件,取周期旋转角ψ为18°,即采用整体模型的1/20进行求解,其3D网格模型如图4(b)所示。考虑到涡流的趋肤效应,在涡流盘上设置边界层网格,对其表面与边沿处生成的高度各向异性网格进行控制,层数为3层,如图4(c)所示,厚度为涡流等效趋肤深度Δ,其计算公式为

式中:μ为涡流盘的磁导率,H/m;ω为涡流盘的旋转角速度,rad/s。
建立三维模型、赋予材料特性、划分网格和设置边界条件后,对电磁场数值模型进行求解。下面对缓速器不同转速和不同气隙条件下的电磁场进行瞬态计算,研究缓速器的气隙磁通密度、感应涡流密度和制动力矩。转速n=1500r/min时不同气隙下的气隙磁通密度分布如图5所示。从图中可看出,缓速器静止时永磁体对应位置的气隙磁通密度均匀分布,而工作时涡流盘进入永磁体一侧的气隙磁通密度被减弱,另一侧却略有增强,总气隙磁通密度被涡流磁动势减弱。随着气隙δ的减小,气隙磁通密度不断增大,且由于涡流磁动势增大,导致气隙磁通密度减弱的部分更为明显。
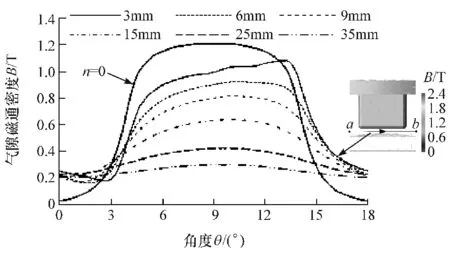
图5 不同气隙时气隙磁通密度分布
由感应涡流密度J可得缓速器的损耗功率为

式中:V为涡流盘体积,m3;ρe为涡流盘电阻率,Ω·m。
转速为1 500r/min时不同气隙下的涡流盘中感应涡流密度分布如图6所示,涡流集中在永磁体宽度方向边线对应的涡流盘部分,随着气隙的增大,涡流密度变得越来越小,则损耗功率随之变小。
缓速器制动力矩T与涡流盘损耗功率P的关系为

图6 不同气隙时感应涡流密度分布图

由图6、式(5)和式(6)可知,随着气隙的增加,同一转速下涡流盘中的感应涡流密度和损耗功率越来越小,制动力矩也随之减小,当δ=40mm时最大制动力矩约10N·m,该值为永磁缓速器的残余力矩。不考虑温度影响时,不同气隙下缓速器制动转矩随转速变化的仿真曲线如图7所示。由图可见,同一气隙下,随着转速提高,气隙平均磁通密度不断减小,进而涡流感应磁通密度也减小,制动力矩逐渐达到饱和值。
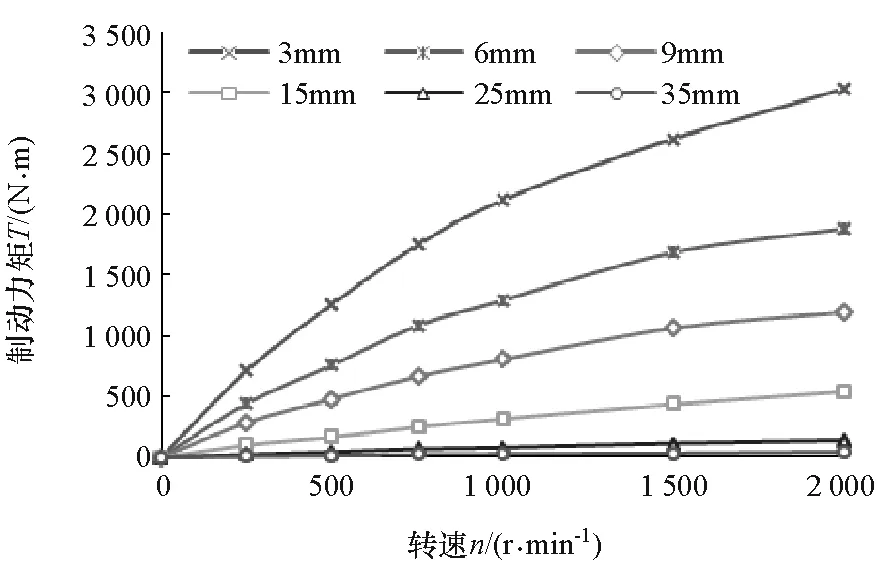
图7 不同气隙时制动力矩仿真曲线
涡流盘与永磁盘之间的吸力会影响力矩调节机构的工作。不同气隙时缓速器涡流盘与永磁盘之间的吸力随转速变化的曲线如图8所示。由图可见:同一气隙下,随着转速的增加,感应涡流密度逐渐增大,涡流盘感应磁场削弱永磁磁场,吸力逐渐减小;同一转速下,吸力随着气隙的增大而减小。
3 温度场数值分析
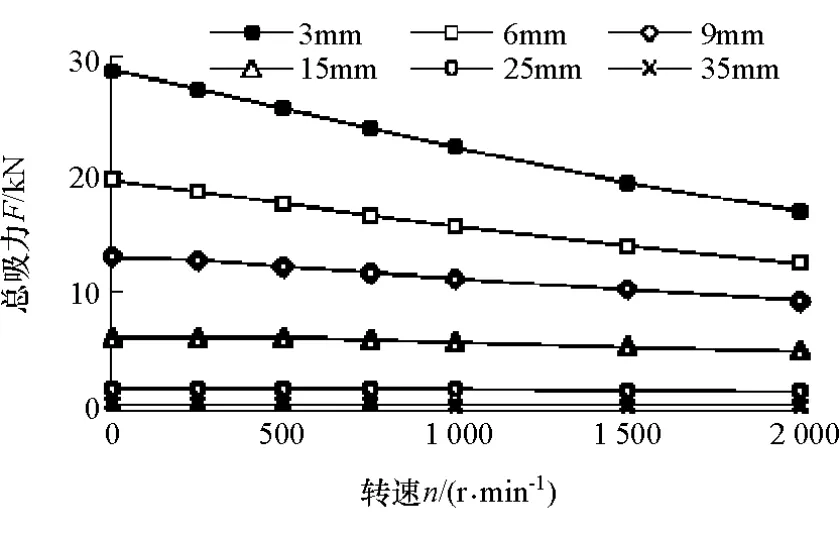
图8 不同气隙时吸力随转速变化曲线
永磁缓速器是利用涡流制动原理将汽车的动能转化为涡流盘的热能,并通过风冷强制对流进行散热。一方面,制动所产生的大量热能使涡流盘温度急剧升高,使涡流盘材料的电磁特性发生改变,降低了缓速器的制动性能;另一方面,涡流盘中的热量通过气隙传递到永磁盘,使永磁体温度升高,一旦超过钕铁硼材料的工作温度,永磁体将发生不可逆失磁。因此,有必要对永磁缓速器的温度场进行分析。
3.1 温度场数学模型
缓速器工作时产生的热能通过热传导、热对流和热辐射3种传递方式散发出去。风冷型缓速器主要利用涡流盘上的散热装置进行热传导和强制对流换热,其中一部分热量通过热对流和热辐射的方式传递到永磁盘中,引起永磁体温度升高。为简化计算模型,做了以下假设:(1)各部件为各向同性导热介质;(2)部件的接触部分为紧密接触,不考虑接触表面的热阻;(3)环境流体为标准大气压下的干燥空气,且温度保持不变。
考虑到涡流制动的趋肤效应,将涡流盘虚拟划分为内热源区和非内热源区,假设热量均布于内热源区,即涡流等效趋肤深度Δ内。根据以上分析,利用周向展开方法建立如图9所示的数学模型。
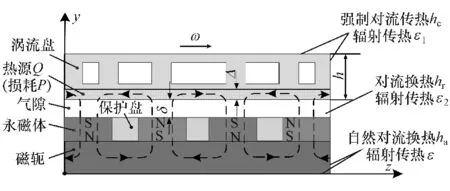
图9 缓速器温度场数学模型
涡流盘内部和各接触部件之间基本上以热传导的方式进行热量传递,其基本方程为

式中:Qc为传导的热流量,W;λ为热导率,W/(m·℃);A为热传导面积,m2;Δtm为热传导平均温差,℃;δ为热传导距离,m。
各部件与环境空气之间主要以热对流和热辐射的方式进行热量传递,其基本方程为
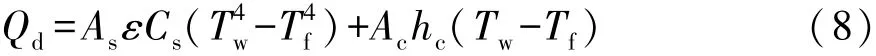
式中:Qd为热传导的热量,J;A为传热面积,m2;ε为表面发射率;Cs为黑体辐射常数;hc为对流换热系数,W/(m2·℃);Tw和Tf分别为表面温度和环境空气温度,℃。
缓速器温度场的分布是电磁场和流场共同作用的结果,利用等效散热系数的经验公式难以精确计算温度场分布,因此本文中通过流场计算得到散热系数的精确解,且风冷式缓速器工作时涡流盘温升较高,应采用导热、对流和辐射耦合的方式对温度场分布进行修正,故引入离散坐标辐射模型,进而求解得到温度场的具体分布。引入k-ε湍流模型,流体湍动动能k和湍动能耗散率ε的方程[15]分别为
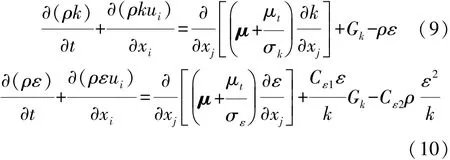
式中:ρ为流体密度,kg/m3;t为时间,s;ui为时均速度,m/s;xi和 xj为速度矢量分量,m/s;μ为速度矢量,m/s;Gk为湍流产生率;μt为湍流黏性系数,μt=和 Cε2为经验常数;σk和 σε分别为 k和ε的普朗特数。
3.2 温度场数值模型
建立包含涡流盘、永磁体、保护盘、磁轭、散热装置和环境流体在内的缓速器温度场仿真模型,如图10(a)所示。设置环境流体为动域和静域两个区域,由于模型具有周期性,取1/20进行计算,其网格划分模型如图10(b)所示。
本模型涉及旋转流动,可采用RNG k-ε湍流模型进行瞬态计算,模型中各部件材料的热物理性质如表2所示。
将电磁场中计算得到的涡流损耗作为热源,生热率公式为

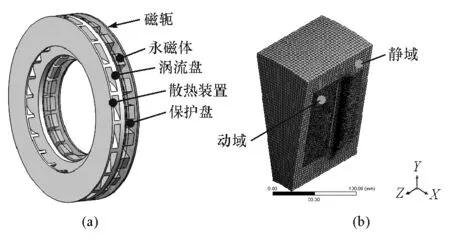
图10 温度场计算模型和1/20网格划分模型
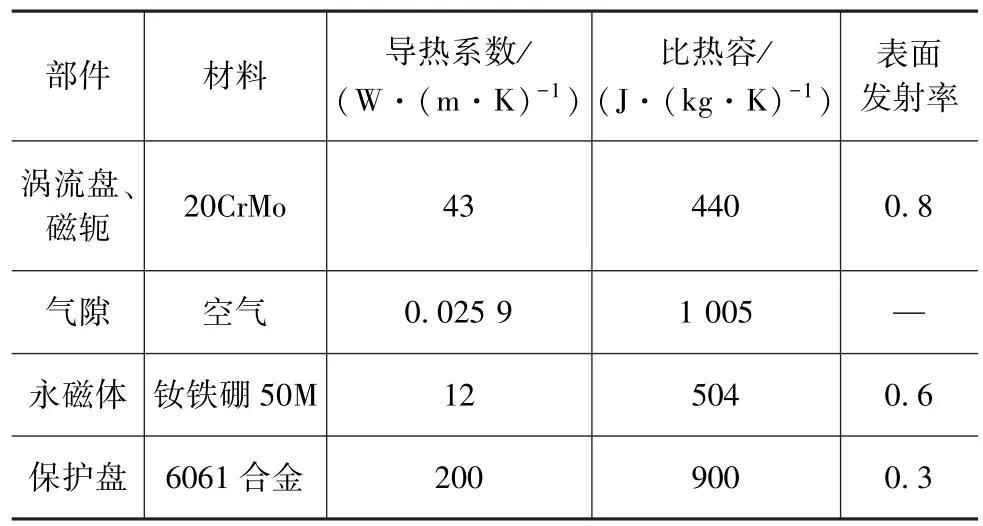
表2 各部件的热物理性质
由数值模拟缓速器在环境温度30℃、气隙9mm和转速750r/min下持续制动时瞬态温度场,得到第12min时缓速器各部件温度分布,如图11所示。由图可见:涡流盘最高温度位于轴向气隙内侧达450℃,径向外侧温度空气流速较大,因此温度低于径向内侧;热量通过对流和辐射传递到永磁体和保护盘上,温度径向分布趋势与涡流盘一致,但整体温差较小,永磁体最高温度为54℃,未超过钕铁硼50M的最高工作温度(tw=100℃)。
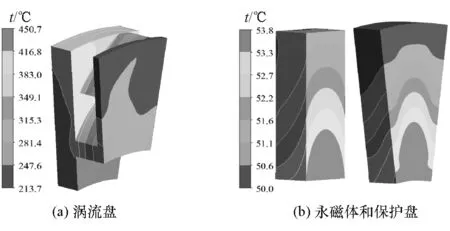
图11 缓速器各部件温度分布云图
图12 为气隙δ=9mm时涡流盘内热源区平均温度和不同气隙时永磁体温度随时间变化曲线。假设车辆在0-12min内缓速器持续制动,第12min时停止制动,12-40min内涡流盘随传动轴继续旋转散热。由图可知:(1)δ=9mm时涡流盘内热源区平均温度在3min时已达到270℃,之后上升减缓,12min时达到432℃,停止制动后温度基本呈直线趋势下降,40min时为111℃,永磁体温度上升先缓后快,这是因为随涡流盘温度的升高,热量对流和辐射加速,12min时达到54℃,停止制动后由于对流和辐射的存在温度仍略有升高,20min后温度开始缓慢下降,40min时温度为46℃;(2)随着气隙的减小,永磁体温度越来越高且上升速度增大,δ=6mm时永磁体温度在12min升至83℃;δ=3mm时永磁体温度在7.5min开始超过 tw=100℃,在 12min温度高达154℃,永磁体将出现不可逆失磁。由于在δ=3~6mm之间未做进一步的细化仿真,无法断言,故为保险起见,缓速器持续制动12min时建议气隙应不小于6mm。
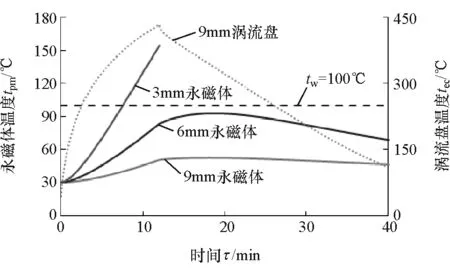
图12 永磁体和涡流盘温度随时间变化曲线
4 磁-热耦合数值分析
4.1 磁-热耦合数学模型
缓速器多场耦合模型可由相应物理场的基本方程及其界面约束关系导出,数学模型可通过分析场间物理量的作用关系得出,本文中主要研究缓速器的磁-热耦合场,其数学描述为
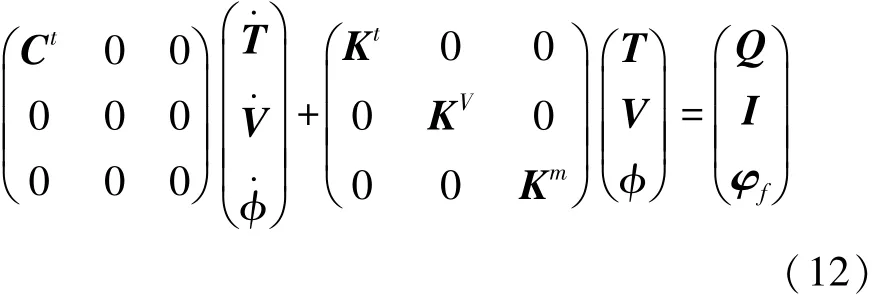
式中:T,V和φ为温度场、电场和磁场的主自由度,即温度阵、电势阵和标量磁势阵;Q,I和φf为已知的各场载荷阵,即热载荷阵(包括节点热流率、热生成率等)、节点电流载荷阵和磁场载荷阵(包括场源磁通量、节点磁通量等);Ct为比热系数阵;Kt为传导和对流系数阵;KV为电导率系数阵;Km为标量磁势系数阵。
从矩阵方程可知,磁-热耦合是子系统关联或结构模块集成形成的耦合,其建模和求解方法为根据各场基本方程建立数学模型后利用数值方法进行求解。
4.2 磁-热耦合数值模型
为计算得到缓速器更准确的制动力矩特性曲线,本文中采用双向耦合法建立磁-热耦合数值模型,包括电磁场、温度场和流体场等多物理场,利用数值模拟的方法对各物理场进行耦合计算,其计算流程如图13所示。
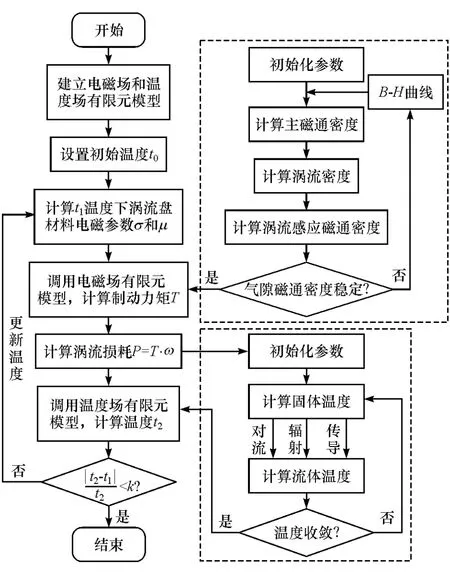
图13 耦合计算流程图
耦合计算流程说明如下。
(1)分别建立缓速器的电磁场和温度场有限元模型,设置初始温度,计算涡流制动损耗功率,并将其作为热源计算温度场,得到更新温度后涡流盘材料的电导率σ和磁导率μ,以此为影响因子重新计算电磁场,经多次迭代,温度误差小于k后,停止计算。
(2)电磁场计算中,由初始化参数计算主磁通密度,得到涡流密度和涡流感应磁通密度,进而得到合成气隙磁通密度,迭代过程中考虑涡流盘材料磁导率μ的非线性(即B-H曲线)和温度的影响。图14为永磁体钕铁硼50M随温度变化的B-H曲线。
(3)涡流盘材料电导率σ与其电阻的关系为

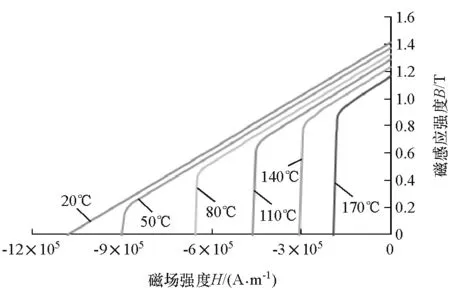
图14 永磁体钕铁硼50M的B-H曲线
电阻随温度呈线性变化,计算公式为

式中:R和R0分别为温度t和t0时的电阻值,Ω;α为电阻温度系数。
(4)温度场计算中,固体与流体之间通过对流、辐射和传导3种方式进行换热,迭代计算至温度收敛为止。
5 试验研究
5.1 缓速器试验平台
永磁缓速器台架试验平台如图15和图16所示,它主要由拖动系统和测量系统组成,包括拖动电机、离合器、汽车变速器、永磁缓速器、高精度转矩转速传感器、温度传感器(包括热电偶式和红外非接触式)和特斯拉计等,满足对不同试验模块的试验要求。为分析缓速器的制动力矩特性、温升特性和持续制动特性,试制了不同材料涡流盘、不同散热结构的多个永磁缓速器样机,并利用转矩转速传感器、温度传感器和特斯拉计等仪器采集试验系统的转速、制动力矩、温度和磁通密度等参数。
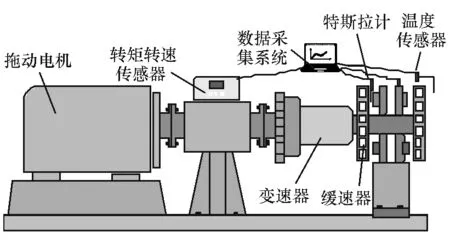
图15 缓速器台架试验平台示意图
5.2 制动力矩特性试验

图16 缓速器台架试验平台
加工涡流盘材料为20CrMo、风道式散热结构的缓速器样机,对气隙从35到3mm选取样点进行台架试验,记录转速为750r/min时持续工作的制动力矩曲线,如图17所示。从图中可以看出:温度对制动力矩影响很大,未考虑温度的仿真值和试验值的最大误差为38%;而考虑温度影响的双向耦合法,制动力矩计算更接近试验值;但双向耦合值仍存在一定误差,最大为8.6%,误差可能来源于耦合仿真模型中没有考虑永磁体由于高温产生的部分失磁,以及模型的简化,因为实际制动试验中永磁体钕铁硼50M的温度曾超过tw=100℃;随着气隙的增大,涡流盘中的温升逐渐减小,两种仿真值与试验值的误差也随之减小。
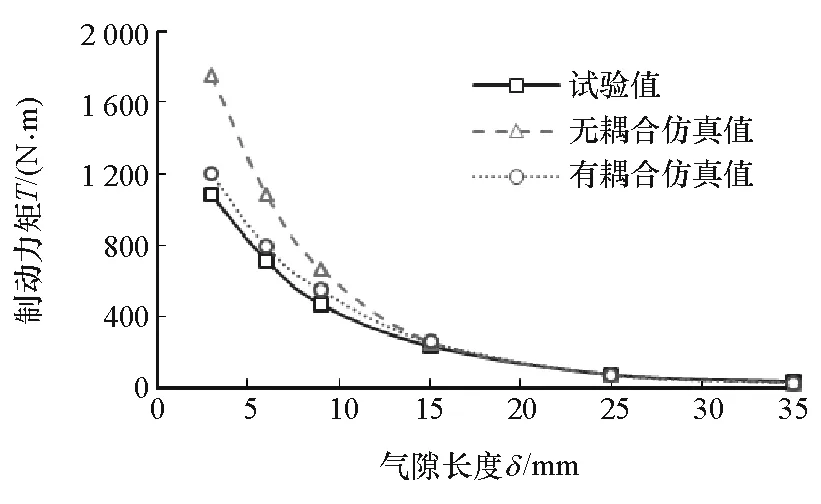
图17 制动力矩仿真与试验结果对比
为考察永磁体失磁情况,对缓速器进行持续制动12min试验,试验后测得永磁体温度高达150℃,已经导致失磁。在同一室温(30℃)下测得试验前后的气隙磁通密度如表3所示。可以看出,试验后永磁体由于温升出现了部分不可逆的失磁,气隙磁通密度下降10.3%。
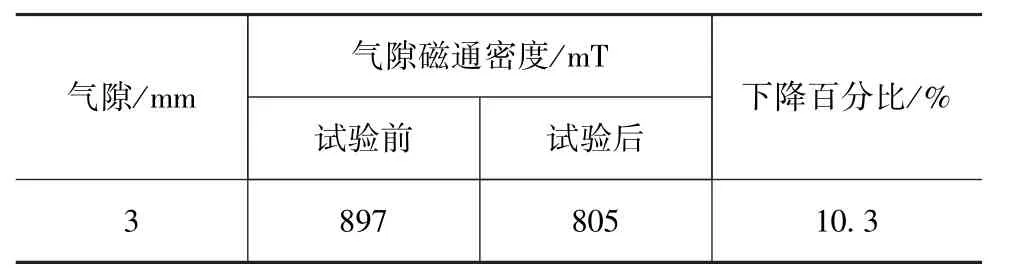
表3 _试验前后气隙磁通密度对比表
5.3 涡流盘材料对制动力矩影响试验
涡流盘是缓速器磁路的主要组成部分,其材料对制动力矩有很大影响。选取紫铜T1、黄铜H62和碳钢20CrMo等3种材料试制涡流盘进行试验,3种材料的电导率依次减小,如表4所示。

表4 涡流盘不同材料电导率
为考察涡流盘材料属性对制动力矩影响,试验中先将转速提升到测试值,然后迅速将缓速器置于最大挡位即气隙为3mm,读取最大制动力矩作为冷态制动力矩,3种材料涡流盘的缓速器冷态时制动力矩随转速变化的曲线如图18所示。从图中可以看出:涡流盘采用T1和H62高电导率的材料时制动力矩分别在转速为150和400r/min时达到最大值,随后逐渐减小,这是因为电导率高的材料在低转速时可产生更强涡流,但随转速增大,涡流感应磁场削弱永磁磁场,造成制动力矩迅速下降;采用20CrMo材料时制动力矩在转速为1 000r/min时为1 790N·m,之后上升平缓,最大制动力矩达到2 080N·m,比采用T1和H62材料时略大。
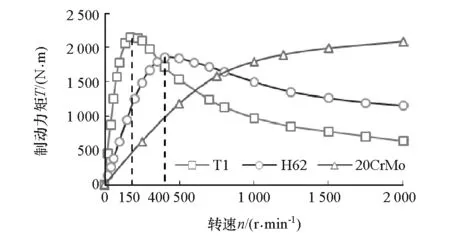
图18 不同涡流盘材料冷态时制动力矩曲线
重载货车在60km/h行驶速度时传动轴转速约为1 500r/min,要使车辆在1 000r/min时获得较大的制动力矩,涡流盘应选用导磁性能好、剩磁少和易于加工的合金钢或碳钢材料;而应用在涡流传动或调速技术方面,选用电导率高的铜材料可在低滑差转速时获得最高的传动力矩。
5.4 持续制动温升特性试验
综合考虑缓速器的散热效果、制造成本和安装使用等因素,提出风道式和翅片式两种结构的涡流盘散热装置,对两种散热装置进行相同条件下的试验,试验条件为:750r/min转速、9mm气隙和持续制动12min。试验结果与仿真结果对比如图19和图20所示。从图中可以看出:(1)采用翅片式散热结构时,涡流盘监测点温度在8min后趋于平稳,温度达到260℃,永磁盘监测点温度在12min时上升至60℃,制动力矩下降32%,可见温度对制动力矩的影响非常大,故分析缓速器制动特性时必须采用磁热耦合计算方法;(2)涡流盘和永磁盘的温度仿真值与试验值吻合较好,最大误差为9.5%,这可能来源于温度测量;(3)采用翅片式散热装置的缓速器制动力矩较大,温升较低,即翅片式散热装置的散热效果优于风道式。
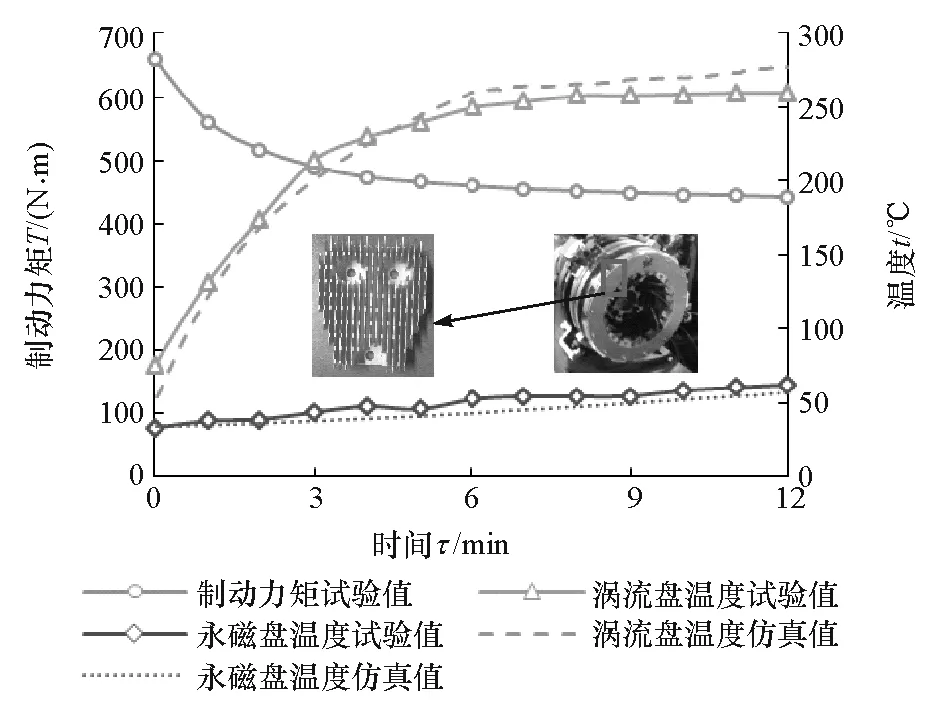
图19 翅片式散热装置温度-时间特性曲线
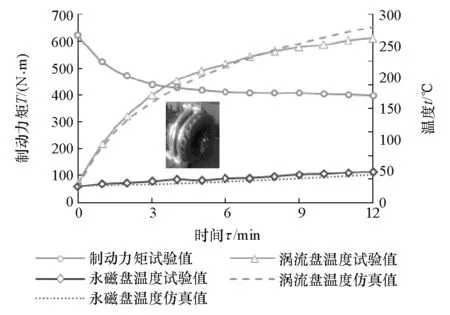
图20 风道式散热结构温度-时间特性曲线
6 结论
(1)提出一种制动力矩可无级调节的永磁缓速器,采用磁-热双向耦合法建立了缓速器多物理场模型。所试制的永磁缓速器最大制动力矩为2 460N·m,最小制动力矩为10N·m。
(2)持续制动时温升对缓速器性能影响很大,未考虑温度的仿真值和试验值的最大误差为38%;而考虑温度影响的双向耦合法计算误差最大为8.6%,误差的产生可能来源于耦合仿真模型中没有考虑永磁体由于高温产生的部分失磁。
(3)随着气隙的减小,永磁体温度越高且上升快,工作气隙δ=3mm时永磁体温度在7.5min开始超过tw=100℃,在12min温度高达154℃,永磁体将出现不可逆失磁,缓速器持续制动12min时气隙不能小于6mm。
(4)涡流盘采用低碳钢材料时,制动力矩在转速为1 000r/min时达到较大值且仍在缓慢上升,而选用电导率高的铜材料可在低转速时获得最高的传动力矩,缓速器采用翅片式散热装置制动性能优于风道式。
