考虑轮胎弹性的重型货车越障性能研究∗

魏道高，宋军伟，瞿文明，吴佩宝，居 刚，高宪峰，陈兴华

(1.合肥工业大学汽车与交通工程学院，合肥 230009； 2.清华大学汽车工程系，北京 100084； 3.江淮汽车技术中心，合肥 230601)

前言

野外行驶的车辆,经常要克服台阶、壕沟等障碍[1]。对于重型货车,其跨越台阶的能力通常被认为是评价其通过性好坏的重要指标之一。影响汽车跨越台阶高度的因素,主要有车轮与地面的附着系数、车辆质心位置和轴距等。这些因素在车辆的主要结构型式确定后一般很难改变。因此对这些因素进行研究,以得到数学模型,对其进行数值求解,在方案设计阶段就能对车辆跨越台阶的高度与壕沟的宽度进行预测,以指导车辆的设计。目前关于越障的相关文献中未见考虑计及轮胎弹性,都假设轮胎是刚性的,在越障过程中轮胎不发生变形,这与实际情况不相符,而且轮胎弹性性能是影响越障性能的重要参数[2-7]。车辆在越障过程中,由于轮胎具有弹性,故轮胎半径时刻变化,且很难找到轮胎变形的规律。为了研究轮胎弹性同时简化模型,本文中将仅考虑轮胎的径向弹性性能及其刚度,以含平衡悬架8×8重型货车为样车,建立其越障力学与数学模型,并进行实车计算与试验对比分析。

1 越障基本假设

车辆跨越垂直障碍时一般车速很低,越障过程近似稳态过程,所以可以从静力学的角度来建立越障的数学模型。为了简化计算,选取车轮跨越台阶且刚好与较低地面脱离接触的时刻来进行受力分析,建立作用在车辆上的力和力矩的静态平衡方程,在建立数学模型前进行如下假设[8]：

(1)车辆在硬路面上行驶,并且车速很低,忽略越障过程中阻力的影响；

(2)忽略轴间差速和轮间差速的影响,车辆对称于其纵向轴线,左右轮同步越障；

(3)悬架弹簧在车体上的安装位置成一条直线,弹簧的运动方向与该线垂直；

(4)车架为刚性车架；

(5)各轴轮胎自由半径相等,仅考虑轮胎的径向弹性变形及刚度,且轮胎的径向变形是线性的,各个轮胎的径向刚度相同；

(6)车辆在越台阶时,各轴车轮所受到的地面反作用力垂直于与地面接触的线或面并指向轮心。

2 越台阶数学模型

2.1 1轴越台阶数学模型

8×8平衡悬架重型货车1轴越障的物理模型如图1所示。

图1 1轴越台阶示意图

其中参数说明如下：L-b为1轴轴心到平衡轴轴心的距离；L1为1,2轴轴距；a为整车质心至1轴轴心距离；b为平衡臂长度；R为轮胎自由半径；hc为整车质心到车轮轴心连线的距离；ki(i＝1,2)为1,2轴悬架刚度；k3为平衡悬架刚度；kt为各个轮胎径向刚度；Ni(i＝1,2,3,4)为地面或沟台对i轴车轮反作用力；h为台阶高度；μ为地面附着系数；αi(i＝1,2,3,4)为接触点接触力Ni与水平面夹角；βi(i＝1,2,3,4)为i轴越障时1轴轴心、平衡轴轴心连线与水平面夹角,δi(i＝1,2,3)为各悬架变形量,δti(i＝1,2,3,4)为各轮胎径向变形量。

根据图1所示的受力分析,由竖直方向合力为零、水平方向合力为零和对1轴轮心合力矩为零,可得

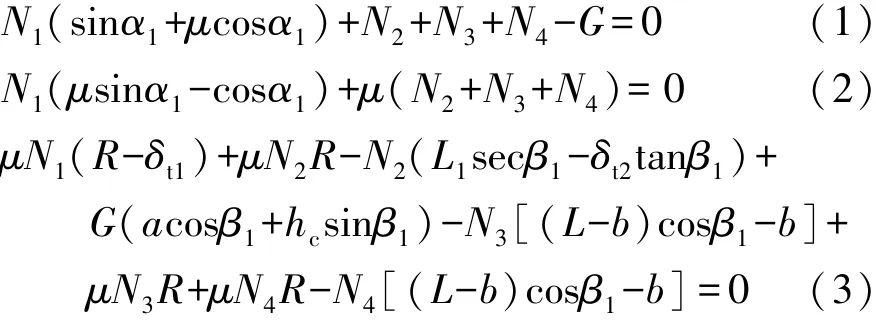
由平衡悬架可得

根据胡克定律知,作用在各车轮的反作用力与悬架弹簧的变形关系为

假设轮胎是线性变形,由胡克定律得到作用在各车轮的反作用力与轮胎径向变形的关系为

各悬架弹簧间的变形关系为

联立式(5)、式(6)和式(8)可得变形协调方程为

其中：

上述式(1)～式(4)、式(7)和式(9)～式(11)即构成了1轴越台阶的数学模型,为非线性方程组,不能直接利用显式求解,可使用牛顿迭代法,利用MATLAB实现算法过程。然后选定G,L,L1,a,b,hc,k1,k2,k3,kt和附着系数μ等参数,即可求解出1轴可以越过台阶的高度h。

2.2 2轴越台阶数学模型

8×8平衡悬架重型货车2轴越障的物理模型如图2所示。图中θi(i＝2,3,4)为i轴越障时2轴轴心、平衡轴轴心连线与水平面夹角。

根据图2所示的受力分析,由竖直方向合力为零,水平方向合力为零和对2轴轮心合力矩为零,可得

图2 2轴越台阶示意图

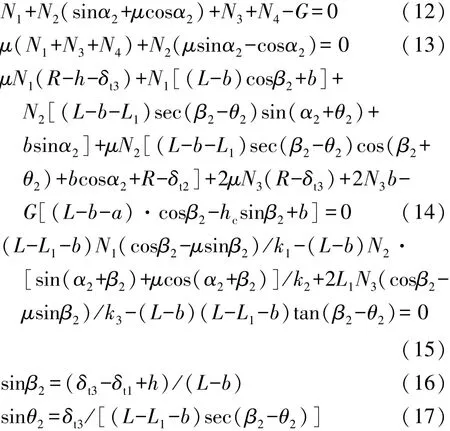
联立式(4)、式(7)、式(10)和式(12)～式(17)即组成了考虑轮胎径向刚度的2轴越台阶的数学模型。通过选定相关的整车参数,即可求得2轴的越台阶高度。

2.3 3轴越台阶数学模型

8×8平衡悬架重型货车3轴越障的物理模型如图3所示。图中γi(i＝3,4)为i轴越障时平衡悬架平衡臂连线与水平面夹角。

图3 3轴越台阶示意图

根据图3所示的受力分析,由竖直方向合力为零、水平方向合力为零和对3轴轮心合力矩为零,可得

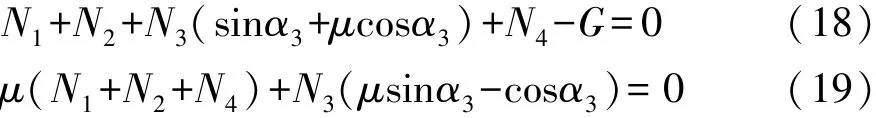
联立式(10)、式(18)～式(25)即组成了考虑轮胎径向刚度的3轴越台阶的数学模型。通过选定相关的整车参数,即可求得3轴的越台阶高度。

2.4 4轴越台阶数学模型

8×8平衡悬架重型货车4轴越障的物理模型如图4所示。

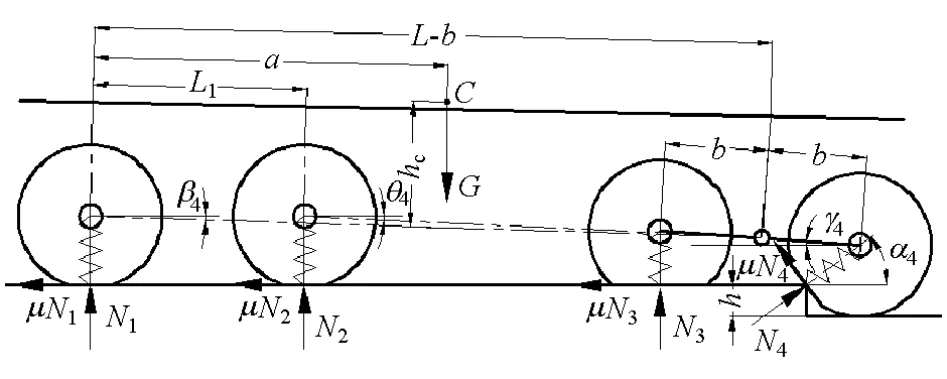
图4 4轴越台阶示意图

根据图4所示的受力分析,由竖直方向合力为零、水平方向合力为零和对4轴轮心合力矩为零,可得

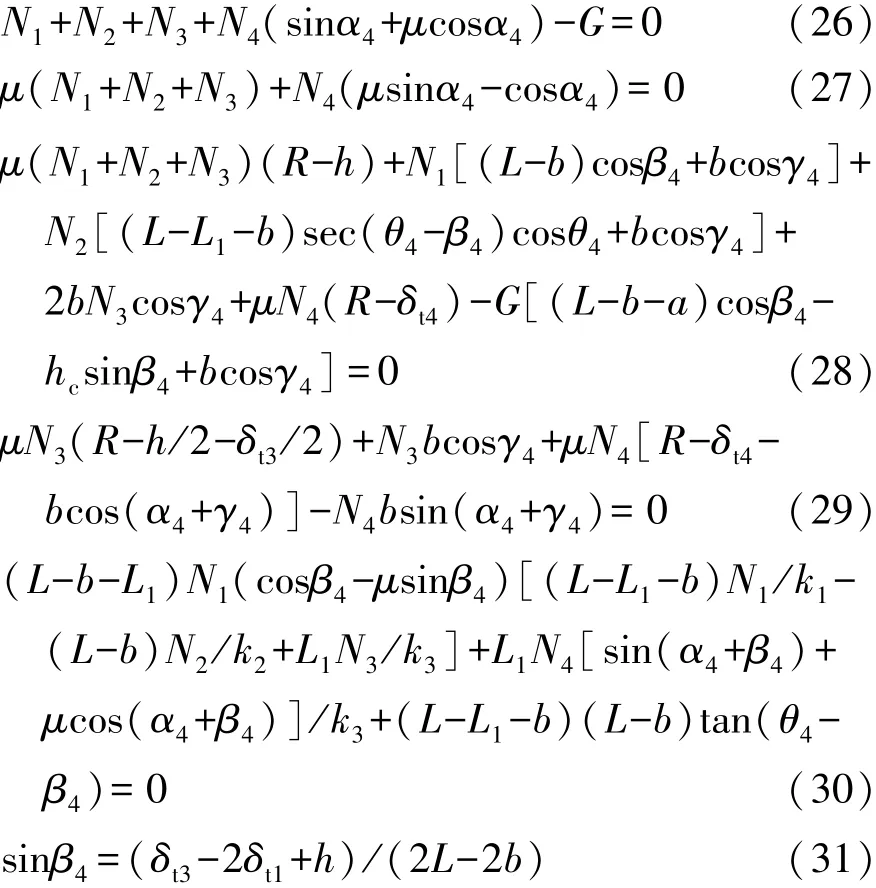
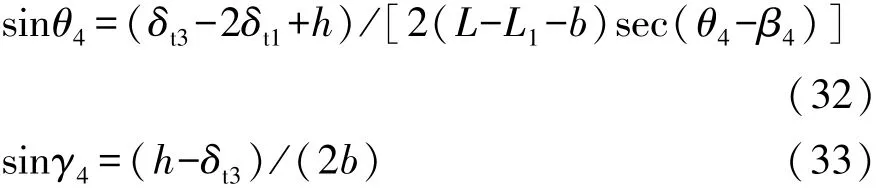
联立式(10)和式(26)～式(33)即组成了考虑轮胎径向刚度的4轴越台阶的数学模型。通过选定相关的整车参数,即可求得4轴的越台阶高度。

3 刚性胎越障计算模型简述

刚性胎的车辆越障模型的建立方法与弹性胎类似,只是将轮胎视为刚性,忽略其变形,车辆各轴的越障物理模型如图5～图8所示,其中参数说明同前所述。由于篇幅限制,本文中仅列出刚性胎车辆1轴的越台阶数学模型。

图5 刚性胎1轴越台阶示意图

图6 刚性胎2轴越台阶示意图

图7 刚性胎3轴越台阶示意图

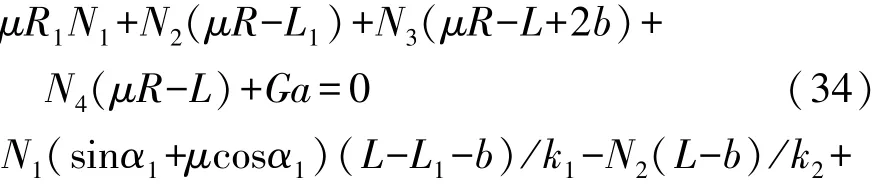
图8 刚性胎4轴越台阶示意图

联立式(1)、式(2)、式(4)和式(34)～式(36)即得刚性轮车辆1轴越台阶数学模型。

4 实例计算与试验

4.1 两种模型计算与试验对比

以国产某型8×8后平衡悬架重型货车作为计算实例,其计算所需参数见表1。为了验证模型的准确性,计算了车辆各轴越台阶的能力并与试验值进行了对比,对比结果如表2所示。其中,试验所用的台阶是混凝土台阶,良好的干燥混凝土路面附着系数为0.7～0.8,在本次计算中取附着系数平均值0.75[9]。整车理论越台阶高度取车辆各轴越台阶高度的最小值。

表1 某8×8型重型货车的整车参数

表2 μ＝0.75时样车越台阶计算高度与试验值

从表2可以看出,理论模型与实车还有一定的差距,但考虑轮胎弹性较假设轮胎为刚性的模型与试验值更接近,表明了模型具有较好的准确性,可以更加准确地预测车辆的越障高度。

4.2 轮胎弹性越台阶高度分析

由上述两种模型计算与试验对比可知,弹性轮胎模型较准确,因此,对该模型计算结果进一步分析。

4.2.1 越台阶高度与附着系数的关系

当路面附着系数μ取0.1～1时,绘制出的各轴越台阶高度随附着系数的变化曲线如图9所示。

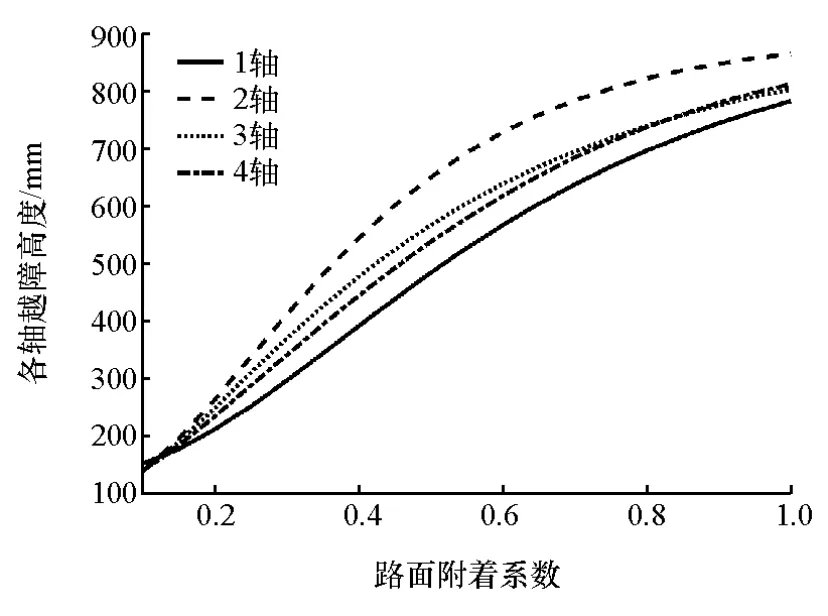
图9 各轴越台阶高度与附着系数的关系

由图9可见,随着路面附着系数从0.1增大到1,各轴的越台阶能力都得到很好的提高。其中,2轴的越台阶能力最好,1轴在正常路面情况下越台阶能力最差,而3轴和4轴的越台阶能力相接近。

4.2.2 越台阶高度与质心位置的关系

在研究各轴越台阶的高度与质心位置的关系时,取附着系数μ＝0.8,改变整车质心到1轴轴心的距离a,绘制出的各轴越台阶高度随质心位置的变化曲线如图10所示。

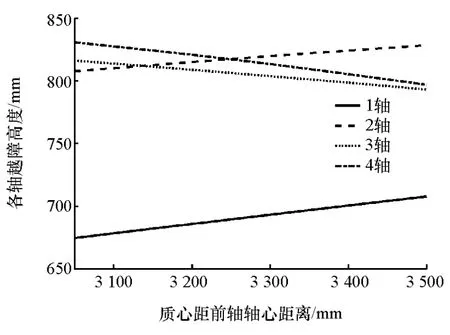
图10 各轴越台阶高度与质心位置的关系

由图10可见,整车质心位置后移时,1,2轴越台阶高度增大,3,4轴越台阶高度减小。

4.2.3 越台阶高度与质心高度的关系

取附着系数μ＝0.8,绘制出的各轴越台阶高度随质心高度的变化曲线如图11所示。

由图11可见,各轴越台阶高度随质心高度变化的幅度都很小。可认为质心高度对整车越台阶能力影响很小,可忽略不计。

图11 各轴越台阶高度与质心高度的关系

5 结论

(1)合理地提出假设,简化了8×8型越野重型货车的越障模型,建立了考虑轮胎径向弹性的车辆各轴越台阶的数学模型。

(2)应用建立的数学模型对国产某型8×8重型货车的各轴的越台阶能力进行了计算。计算发现,考虑轮胎为弹性的模型与轮胎为刚性的模型相比,所计算的整车越台阶高度与试验值更加接近,表明了模型的准确性。

(3)分析了路面附着系数、整车质心位置、整车质心高度对车辆各轴越障能力的影响。随着路面附着系数增大,各轴的越台阶能力都得到很好的提高；整车质心位置后移时,1,2轴越台阶高度增大,3,4轴越台阶高度减小；整车质心高度对整车越台阶能力影响很小。