基于三大策略 渗透数学思想

李琼珍

[摘要]在小学数学课堂教学实践中，教师应善于发掘数学知识的思想层面，在日常教学中渗透数学思想。一方面要创设情境展开深入发掘，突出数学思想的重要性;另一方面，在新知的学习阶段，要加大对学习过程特别是数学思想的关注;除此之外，还要在延伸阶段不断深化学生对数学思想的认知与运用。具体而言，要深挖教材，在情境中渗透数学思想;关注过程，在学习中渗透数学思想;强调运用，在练习中渗透数学思想。

[关键词]小学数学;数学思想;渗透

伴随着新课程改革的不断深入，数学教学逐渐加大了对三维目标的关注。根据《数学课程标准》（2011版）中的相关规定，基本数学思想已经成为教学中不可忽视的重要基础目标。在当前的小学数学教学中，教师只重视数学基础知识和技能的传授是远远不够的，还要引导学生掌握数学思想方法。这就要求教师在日常教学中要善于发掘数学知识的思想层面，积极渗透数学思想，培养小学生数学综合能力。

一、深挖教材——在情境中渗透数学思想

当前，在小学数学教学实践中，情境图的应用越来越广泛。以北师大版小学数学教材为例，其典型特征就是基于“情境图+问题串”的方式向学生展示数学信息。教师应注意的是，情境的创设绝不可毫无目的，应当结合教材内容深入发掘，由此才能够充分凸显蕴含在情景图中的数学思想。

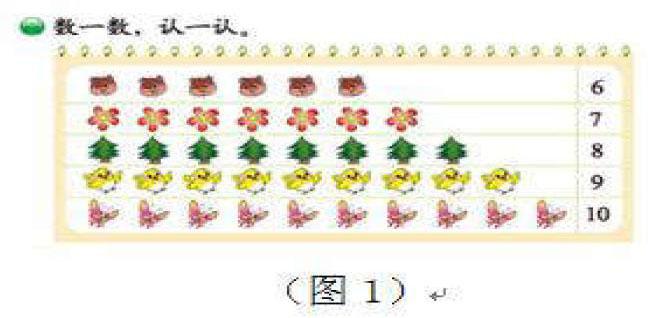
例如，在一年级上册教材中设置了如下情境图（图1），目的就是为了使学生通过对情境图的认知，感受物体所对应的个数，由此形成“6～10”的概念。

在情景图中所展现的物体都是小学生能够在生活中经常见到的，实际上这也渗透了很多数学思想：1.集合的思想。与一个数字相对应的是一类物体，这类物体就能够形成一个集合。2.一一对应的数学思想。在情境图中，每一种物体的集合都与一个自然数相对应，为学生提供了数数的载体。在教学实践中，教师应当给予学生正确的引导，让学生在数数的过程中感受集合思想和一一对应思想，全面系统地提升学生的数学素养。

二、关注过程——在学习中渗透数学思想

在小学数学教学实践中，教师应善于渗透数学思想，让学生在习得相应知识的同时，体会到数学思想的独特魅力。

1.在新知学习中渗透数学思想

《数学课程标准》特别强调，数学教学应结合学生的生活经验，将实际问题抽象演变成为数学模型，使学生可以亲历完成解释和应用的这一过程。小学生对数学知识的学习过程，实际上正是对数学模型的理解与把握的过程。在这一过程中，教师应善于引导学生从中体会数学思想，提升教学实效。

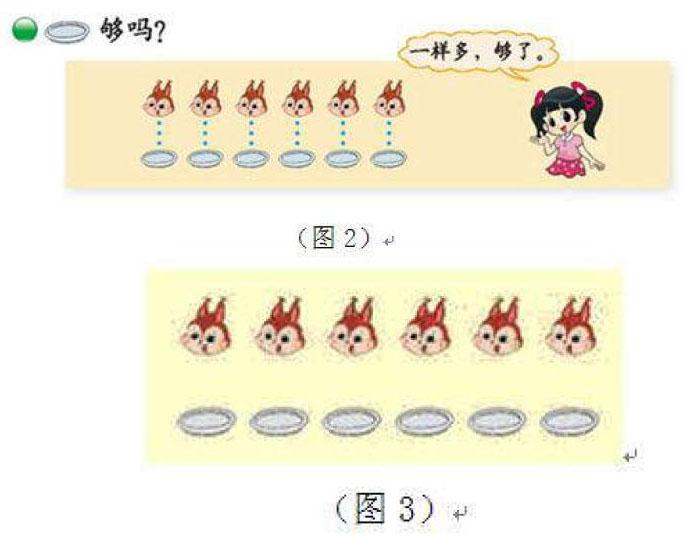
例如，一年级上册教材第14页中所呈现的情境图是“小松鼠分盘子”（图2），这幅图意在引导学生感受数学概念“一样多”。

关于物体个数的比较，学生在幼儿园的时候就已经有所接触，但是，他们的理解往往相对浅显，通常是基于对数量的比较或者基于自己的感觉。在实际教学实践中，教师应通过如下方式帮助学生树立正确的“同样多”的概念（图3）。

师：同学们，如果每一个小松鼠吃饭都需要用一个盘子，那么，上面的小松鼠都能够分到各自的盘子吗？

生1：刚好每个松鼠都对应一个盘子。

生2：每只松鼠的下面都有一个，也就是够分。

师：大家回答得都很好。那么，如果让你们借助画图的方法，怎样才能够说明每个松鼠都能分得一个盘子呢？

接下来就是学生的动手操作环节。根据学生所展示的学习成果，教师向学生展示图2。基于小兔和砖块的一一对应关系，学生了解到通过这一方式可以快速有效地对两种物体进行数量比较。之后，教师向学生再一次展示情景图（图4）：

教师向学生布置画图任务，通过画图解决问题：是否每一个小松鼠都能够分得一个勺子和一个杯子？

借助这样的情景，学生在分盘子、勺子以及杯子的过程中，能够利用画图的方式掌握比较大小的方法，还可以充分领悟一一对应的数学思想。

2.在数学探究中渗透数学思想

在课堂教学中，教师应正确引导学生，使学生可以在自主探究的过程中习得数学知识、感悟数学思想。

例如，第八册教材中《梯形的面积》一课，其教学重点在于引导学生自主推导出梯形的面积公式。在具体教学实践中，教师普遍采用对接的方式，将两个完全相同的平行四边形合成一个梯形，这样学生可以根据已经掌握的平行四边形面积公式自主推导出梯形面积公式。但是，在这一过程中，学生不能充分感悟转化的数学思想，主要是因为图形的转化源自于教师。所以，教师应当将教学重点放置于“如何求梯形的面积”这一问题上，先引导学生进行充分思考：如何才能根据已经学习过的面积公式，实现对梯形面积公式的推导？之后再引导学生进行动手操作实践，自主发现通过两个完全相同的平行四边形的对接可以获得一个梯形。这样的公式推导过程才能够水到渠成，学生才能够印象深刻。当学生充分理解并掌握转化思想之后，教师可以向学生出示题目：1+2+3+4+……+10=？实际上，解决这道题是对初中阶段“连续正整数的求和”相关内容的预教学，既有助于学生运用转化思想，也有助于实现相关知识的渗透。

三、强调运用——在练习中渗透数学思想

1.在运用中渗透数学思想

当学生通过自主学习完成对数学知识的建模之后，引导学生如何利用所学的知识则是教学的关键。在这一过程中，教师应结合教材范例中所蕴含的数学思想进行有效的教学延伸。

例如，二年级上册教材第97页有如下习题（图5），在实际教学过程中，教学重点不仅是完成填空，还需要有效渗透函数的基本思想。在习题2中，不管是先减7再加14，还是先除以3再乘以5，随着被加数和被除数的改变，其结果也会呈现不同的变化，这有助于学生感受数的变化，掌握“即使运算过程没有发生改变，结果仍然变化”这一思想。

2.在解题中渗透数学思想

問题是引导学生展开数学学习的有效载体，解决问题可以帮助学生准确把握相应的知识。为了有效降低问题的难度，可以借助转化的思想。

例如，在数学问题中，最典型的莫过于“鸡兔同笼”。在小学阶段，这一题目的出现是为了引导学生展开数学猜想，并通过验证有效解决问题，在猜想与验证的过程中正是采用了转化的思想。教师可以借助列表的方法，让学生充分领悟转化法的精妙之处，这样既有助于学生掌握相应的数学知识，也能够实现转化思想的有效渗透。

总之，在日常教学中，教师应有意识、有计划地渗透数学思想方法，让学生不但能够掌握相应的数学知识，还能够有效借助数学方法提升自主学习能力。

参考文献：

[1]马生宏.论如何在小学数学教学中渗透数学思想方法[J].吉林教育，2014，（02）.

[2]魏尚忠.浅谈数学思想在小学数学教学中的渗透[J].吉林教育，2014，（02）.

[3]杨丽.让数学思想方法在学生脑海里“扎根”[J].教育教学论坛，2014，（07）.

注：本文系泉州市教育科学“十三五”规划（第一批）课题“小学数学思想方法教学的研究”（立项编号：QG1351-102）的研究成果。

（责任编辑 赵永玲）