Stabilization of discrete-time linear systems by delay independent truncated predictor feedback

Yusheng WEI,Zongli LIN

Charles L.Brown Department of Electrical and Computer Engineering,University of Virginia,Charlottesville,VA 22904-4743,U.S.A.

Received 10 September 2018;revised 9 October 2018;accepted 9 October 2018

Abstract For a discrete-time linear system with input delay,the predictor feedback law is the product of a feedback gain matrix with the predicted state at a future time instant ahead of the current time instant by the amount of the delay,which is the sum of the zero input solution and the zero state solution of the system.The zero state solution is a finite summation that involves past input,requiring considerable memory in the digital implementation of the predictor feedback law.The truncated predictor feedback,which results from discarding the finite summation part of the predictor feedback law,reduces implementation complexity.The delay independent truncated predictor feedback law further discards the delay dependent transition matrix in the truncated predictor feedback law and is thus robust to unknown delays.It is known that such a delay independent truncated predictor feedback law stabilizes a discrete-time linear system with all its poles at z=1 or inside the unit circle no matter how large the delay is.In this paper,we first construct an example to show that the delay independent truncated predictor feedback law cannot compensate too large a delay if the open loop system has poles on the unit circle at z≠1.Then,a delay bound is provided for the stabilizability of a general linear system by the delay independent truncated predictor feedback.

Keywords:Time delay,stabilization,delay independent truncated predictor feedback

1 Introduction

A fundamental problem in control of linear systems with time delay is asymptotic stabilization.Various control techniques have been developed(see[1-18]).In this paper,we consider asymptotic stabilization of a discrete-time linear system with time-varying delay in the input,

where x∈Rnand u∈Rmare the state vector and the input vector,respectively.The time-varying delay r(k):N→N satisfies r(k)?R,where N denotes the set of nonnegative integers,and R∈N is a delay bound.The initial condition is given by ψ(k),k ∈ I[-R,0],where I[a,b]denotes the set of all integers in[a,b]and a,b∈R.It is assumed that(A,B)is stabilizable.

One of the most commonly adopted feedback laws for stabilization of system(1)is the predictor feedback law.When the delay r isconstant,the predictorfeedback law takes the form of

is the predicted state at time instant k+r,which consists of the zero input solution and the zero state solution of the system,and K is designed such that A+BK is Schur stable.Then,the closed-loop system is given by

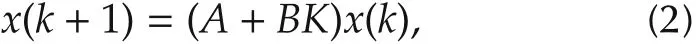
which is exponentially stable.Recall that the predictor feedback law forcontinuous-time linearsystemswith input delay is infinite-dimensional,containing an integral term that takes past input as part of its integrand.The feedback law(2)is finite-dimensional,leading to its easy implementation.However,the finite summation part of the predictor feedback law(2)is the product of the feedback gain matrix K with the zero state solution of the system at the future time instant k+r,requiring past input u(k),k∈I[k-r,k-1],in the digital implementation.To alleviate the implemetation burden,Reference[19]proposed the truncated predictor feedback law

with the finite summation part of the predictor feedback law discarded.Furthermore,the delay independenttruncated predictor feedback law

further discards the delay dependent transition matrix Arin the truncated predictor feedback law.This simplification results in the robustness of(3)to time-varying delays and even unknown delays.It was shown in[19]that the truncated predictor feedback law(2)stabilizes system(1)with allopen loop poleson orinside the unite circle no matter how large the delay r is.Furthermore,the delay independent truncated predictor feedback law(3)stabilizes system(1)with all open loop poles at z=1 or inside the unit circle,again,no matter how large the delay r is.The eigenstructural assignment low gain feedback design technique(see[20])was employed in[19]to construct the feedback gain matrix K,while in[21]and[22],a Lyapunov equation based low gain feedback design was employed,and the same conclusions with those of[19]were reached.

In this paper,we first construct an example to show that the delay independent truncated predictor feedback law cannot compensate an arbitrarily large delay if the open loop system has poles on the unit circle at z≠1.Then,an admissible delay bound under the delay independent truncated predictor feedback law is given for a general linear system that may be exponentially unstable.The results developed in this paper extend their continuous-time counterparts in[23].A preliminary version of the results in this paper was presented in a conference paper[24].

The rest of the paper is organized as follows.Section 2 recalls the delay independent truncated predictor feedback law and its feedback gain matrix design by the Lyapunov equation based method.Section 3 contains the main result.Section 4 presents the numerical examples,and Section 5 concludes the paper.

2 Preliminaries

Consider the delay independent truncated predictor feedback law for system(1)with a controllable pair(A,B)(see[22]),

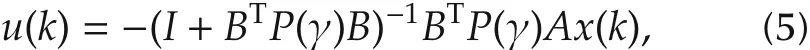
where I stands for the identity matrix,P(γ)is the unique positive definite solution to the discrete-time parametric algebraic Riccati equation,

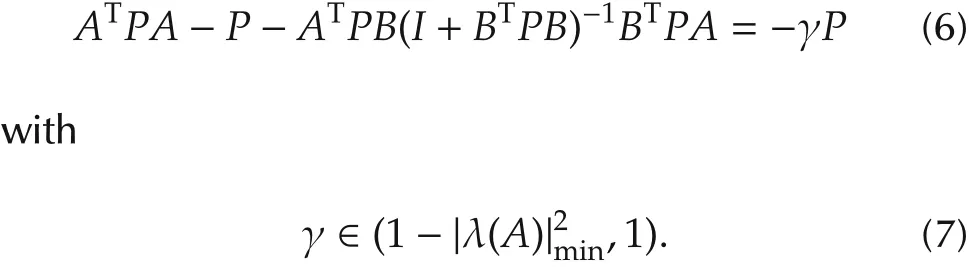
Note that(7)is necessary and sufficient for the existence and uniqueness of P(γ).We now recall a lemma from[25].

Lemma 1[25] For any positive definite matrix P,any integers n1and n2such that n2?n1,and any vector valued function x(k):I[n1,n2]→Rn,we have

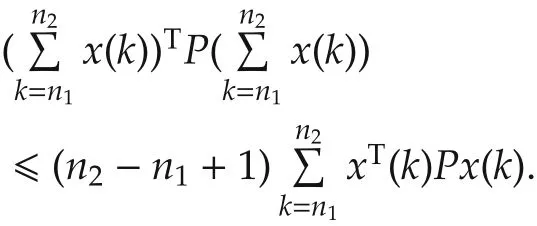
Next,we establish the following two lemmas.The proof of the first lemma is quite similar to those of Lemma 1,Corollary 1 and Corollary 2 in[21],and is thus omitted.

Lemma 2[24]Let(A,B)be controllable with A nonsingular.For each γ ∈ (1-|λ(A)|2min,1),the unique positive definite solution P(γ)to the parametric algebraic Riccati equation(6)satisfies

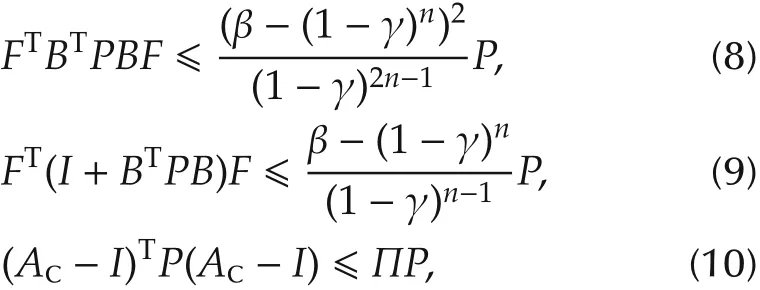
where F=(I+BTPB)-1BTPA,AC=A-BF,β=det2(A)and

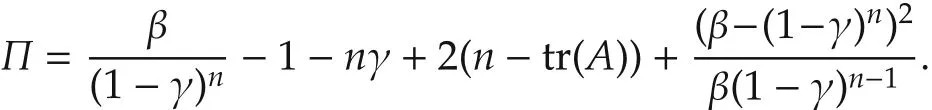
We next establish an inequality in terms of the determinate and the trace of a class of matrices.

Lemma 3 If A ∈ Rn×nhas all its eigenvalues on or outside the unit circle,then,

4det4(A)-6det2(A)+det-2(A)+1+2n-2tr(A)?0.

Proof We use polarcoordinatesto denote the eigenvalues of A as λi=riejθi,where ri?1 and θi∈ (-π,π],for each integer i∈I[1,n].The determinant of A and the trace of A are respectively expressed as det(A)=

where we have used the fact that eigenvalues appear in conjugate pairs.We then have

Define a multivariate function

where ri?1,i∈I[1,n].We observe that g(r1,r2,...,rn)remains unchanged under any permutation of r1,r2,...,rn.Then,we only consider the partial derivative of g(r1,r2,...,rn)with respect to rn,

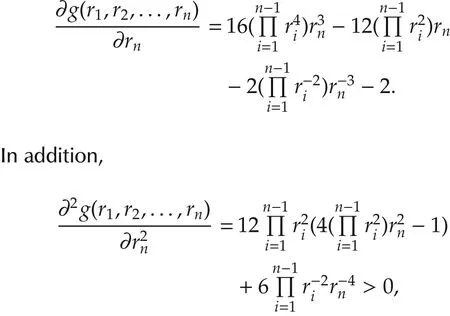
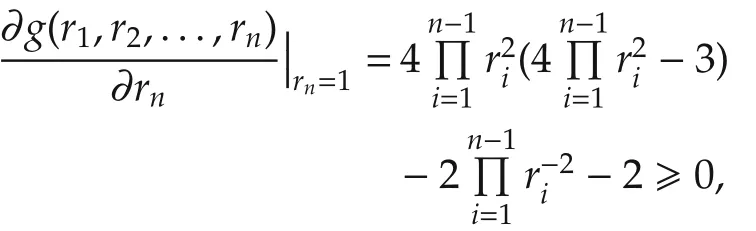
where the equality sign holds if and only if ri=1 for all i∈I[1,n-1].Therefore,

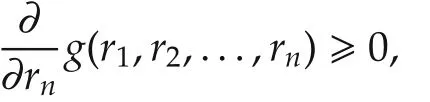
and g(r1,r2,...,rn)is non-decreasing with respect to rn.Then,

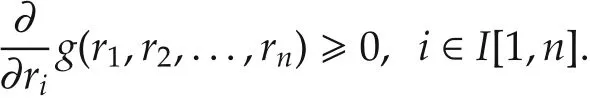
It follows from(11)that

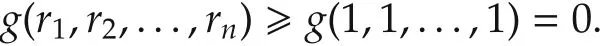
This completes the proof.

Without loss of generality,we assume that the stabilizable pair(A,B)in system(1)has the following decomposed form:

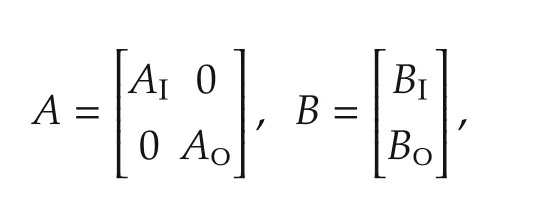
where AI∈ RnI×nIhas all its eigenvalues inside the unit circle and AO∈ RnO×n O has all its eigenvalues on or outside the unit circle.Then,system(1)can be written as

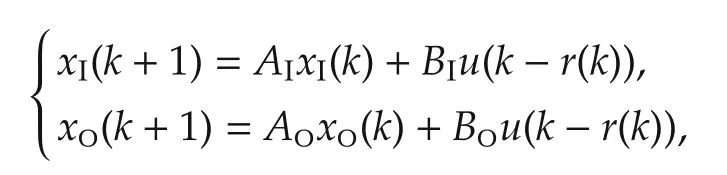
where x(k)=(xTI(k)xTO(k))T.The stabilizability of(A,B)implies that(AO,BO)is controllable.Note that the asymptotic stabilizability of the second subsystem implies that of the whole system because all eigenvalues of AIare inside the unit circle.Thus,without loss of generality,we make the following assumption on system(1).

Assumption 1 The pair(A,B)is controllable with all eigenvalues of A on or outside the unit circle.

3 An admissible delay bound

In this section,we first construct an example to show that if system(1)has open loop poles on the unit circle at z≠1,the delay independent truncated predictor feedback law(5)cannot stabilize the system when the delay is large enough.

Consider system(1)with

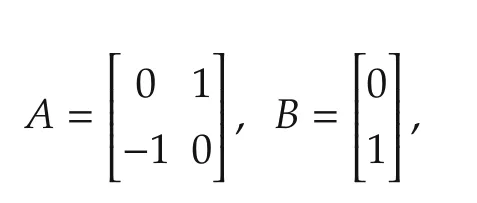
and a constant delay r(k)=2.It can be readily verified that(A,B)is controllable with eigenvalues of A at z=±j.By solving the parametric algebraic Riccati equation(6),we obtain the unique positive definite solution

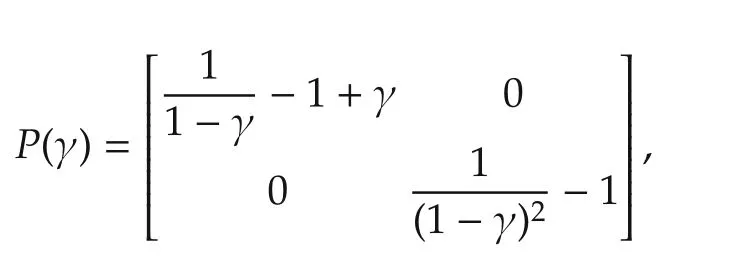
where γ∈(0,1)in view of(7).Hence,the delay independent truncated predictor feedback is given by

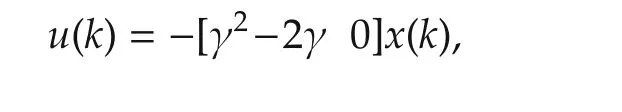
under which the closed-loop system is given by

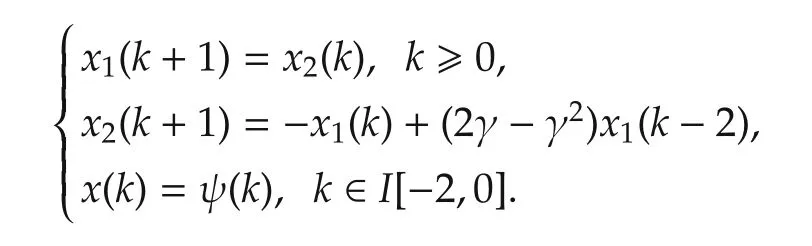
The characteristic equation of the closed-loop system is

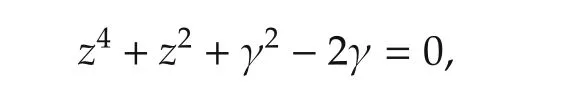
whose four complex roots are

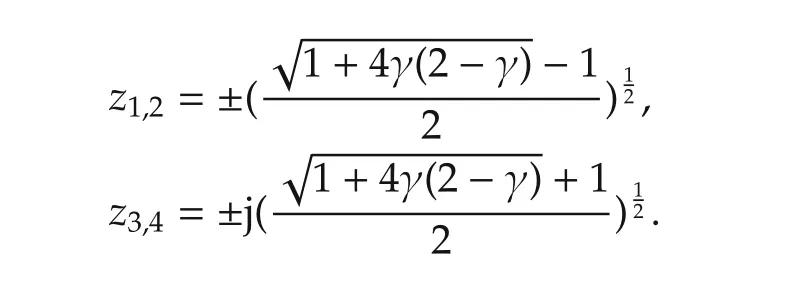
Note that z3and z4both lie outside the unit circle for each γ∈(0,1).Thus,the delay independent truncated predictor feedback law(5)fails to stabilize the system.

We nextestablish a delay bound for generallinearsystems to be stabilizable by the delay independent truncated predictor feedback law(5).

Theorem 1 Let Assumption 1 hold.If

where β and Π are defined as in Lemma 2,then,the delay independent truncated predictor feedback law(5)asymptotically stabilizes system(1).

Proof The closed-loop system under the delay independent truncated predictor feedback law(5)is given by

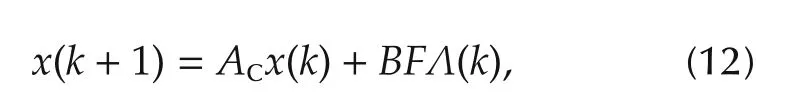
where ACand F are defined as in Lemma 2 and Λ(k)=x(k)-x(k-r(k)).Considera Lyapunov function V(x(k))=xT(k)Px(k).In view of Assumption 1,we let γ∈(0,1)satisfy(7).By Young’s inequality,Lemma 2 and(12),we evaluate the forward difference of V(x(k))along the trajectory of the closed-loop system as follows:

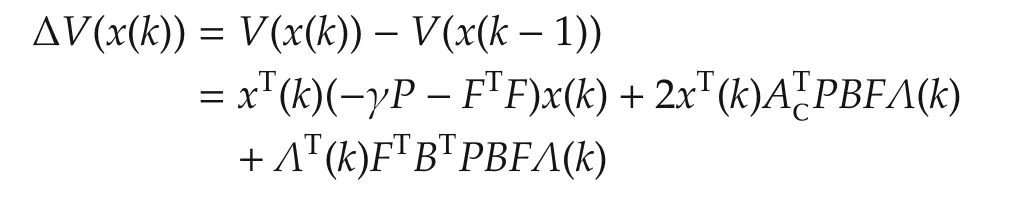
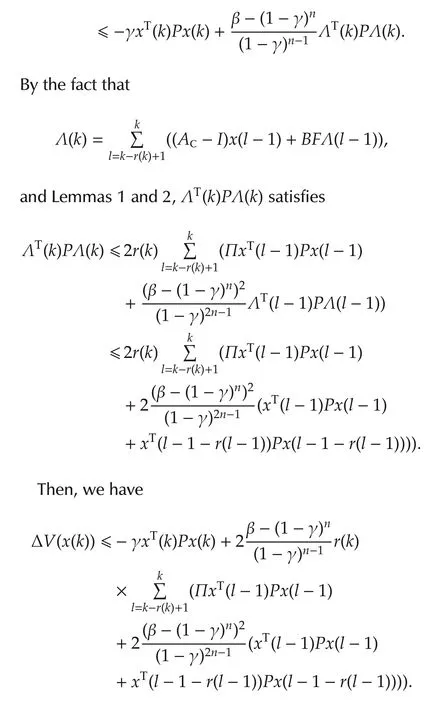
Under the assumption that V(x(k+κ))＜ ρV(x(k))for each κ ∈ I[-2R,0],where ρ ＞ 1 is any positive constant,we obtain

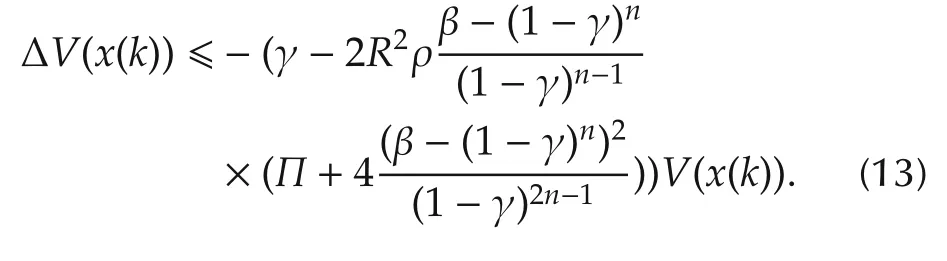
If(11)holds,then,it follows from(13)that ΔV(x(k))?-ϵV(x(k))for some ρ ＞ 1 and some ϵ＞ 0.The asymptotic stability of the closed-loop system then follows from the Razumikhin Stability Theorem.It remains to show that the denominator inside the square root on the right hand-side of(11)is positive.This fact can be trivally verified by the use of Lemma 3 and the facts that β ?1 and γ ∈ (0,1).This completes the proof.

Corollary 1 Let A in system(1)have all its eigenvalues at z=1.Given an arbitrarily large delay bound R,the delay independent truncated predictor feedback law(5)with each γ ∈ (0,γ＊)asymptotically stabilizes system(1),where γ＊is the smallest positive solution to the following nonlinear equation:

Proof If A has all its eigenvalues at z=1,then tr(A)=n and β=1.Thus,(11)is equivalent to(14)with the equality sign replaced by＜.Note that the lefthand side of(14)approaches zero as γ → 0 and goes to infinity as γ → 1,which implies that(14)has a smallest positive solution γ＊.This completes the proof.

Remark 1 The result of Corollary 1 is consistent with those of[19]or[21],where it is established that a discrete-time linear system with all its open loop poles at z=1 or inside the unit circle can be stabilized by the delay independent truncated predictor feedback law(5)no matter how large the delay is.

4 Numerical examples

4.1 Example 1:A system with all poles on the unit circle

Consider system(1)with

The open loop system has a pair of poles on the unit circle at z=0.987±j0.1607 and a pole at z=1.It can be easily verified that(A,B)is controllable with tr(A)=2.974.We pick a time-varying delay r(k)=(1+(-1)k)/2,which is 1 when k is even and is 0 otherwise,and we pick γ=0.0078.The initial condition is given by x(k)=[1-1 0]T,k∈I[-1,0].The state response and the input signal are illustrated in Fig.1,which demonstrates the convergence of the closed-loop signals.

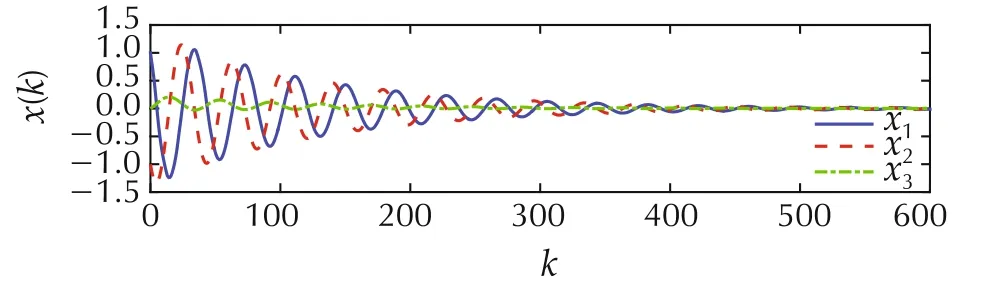
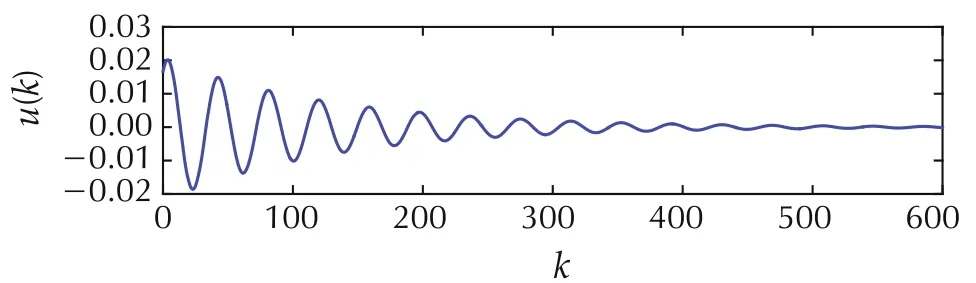
Fig.1 State response and control input under state feedback law(5)with γ=0.0078.

4.2 Example 2:An exponentially unstable system

Consider system(1)with

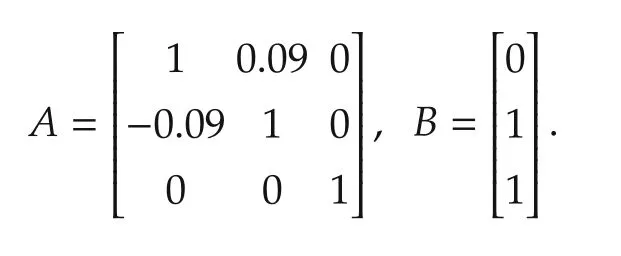
The open loop system has a pair of exponentially unstable poles at z=1±j0.09 and a pole at z=1.It can be readily verified that(A,B)is controllable with det(A)=1.0163 and tr(A)=3.We pick r(k)=(1+(-1)k)/2.With the initial condition given by x(k)=[1-1 0]T,k∈I[-1,0],simulation is run with γ=0.016.The converging state response and the corresponding input signal are illustrated in Fig.2.

Fig.2 State response and control input under state feedback law(5)with γ=0.016.

5 Conclusions

We considered the delay independent truncated predictor feedback law and its stabilization of discrete-time linear systems with time-varying input delay.A example was first constructed to show that such a feedback law cannot compensate a large delay if the open loop system has poles on the unit circle at z≠1.Then,a stability criterion of the closed-loop system in terms of the delay bound was developed for a general discrete-time linear system which may be exponentially unstable.