An output-based distributed observer and its application to the cooperative linear output regulation problem

Tao LIU,Jie HUANG

Department of Mechanical and Automation Engineering,The Chinese University of Hong Kong,Shatin,N.T.,Hong Kong,China

Received 20 August 2018;revised 3 October 2018;accepted 8 October 2018

Abstract In this paper,we first extend an existing stability result for a class of linear switched systems.This extended result will relax the existence conditions of the output-based distributed observer for a leader system subject to jointly connected switching communication networks in the literature.As an application of this output-based distributed observer,we solve the cooperative output regulation problem of a linear multi-agent system subject to jointly connected switching communication networks by composing a purely decentralized control law and the output-based distributed observer based on the certainty equivalence principle.

Keywords:Output-based distributed observer,switched systems,cooperative output regulation

1 Introduction

Nowadays,more and more complex engineering tasks are performed by coordinating the function of a group of individual subsystems.Typical tasks include formation of mobile robots[2,3],attitude alignment of multiple spacecrafts[4,5],mobile sensor area coverage[6,7],and distributed control of electric power grids[8,9].These applications have led to a surge of interest in cooperative control of networked multi-agent systems.A specific feature for the control of a networked multiagent system is that the control law to be designed has to satisfy the communication constraints imposed by the communication network.We call a control law that satisfies the communication constraints as a distributed control law.

The distributed observer approach is one of the effective approaches to synthesizing a distributed control law.It was first proposed in[10]to solve the cooperative output regulation problem of a linear multi-agent system subject to static communication constraints,and then in[11]for handling the same problem subject to switching communication constraints.In contrast with the controller design for a single system,information sharing,or,what is the same,cooperation among different subsystems is essential in the design of the distributed control law for a networked multi-agent system.Thus,the core of the approach in[10]and[11]is the employment of the so-called distributed observer,which can provide,through cooperation,an estimation ofthe leader’s state to each followerso thata distributed control law can be synthesized on the basis of a purely decentralized control law and the distributed observer.Such an approach to designing a distributed control law is known as the certainty equivalence principle.A distinguished feature of the distributed observer approach is that the approach reduces a seemingly intractable task of controlling a complex multi-agent system to a leader-following consensus problem of a special class of linear systems.As a result,it offers a systematic way for handling various cooperative control problems of leader-follower multi-agent systems over various communication networks.Other publications making use of the distributed observer can be found in,for example,[8],[9],[12],and[13].

The distributed observer proposed in[10]and[11]is state-based in the sense that the observer relies on the state ofthe leadersystem.In practice,itmay happen that only the outputratherthan the state ofthe leadersystem is available.Thus,in this paper,we will further consider the design of a distributed observer subject to jointly connected switching communication networks thatonly uses the output information of the leader system.We call such a distributed observer an output-based distributed observer.For this purpose,we will first extend the stability result for a class of linear switched systems studied in[14]by relaxing the symmetry assumption ofa switching matrix to Assumption 1,which includes some interesting non-symmetric cases.This result lends itself to a synthesis of an output-based distributed observer,subject to jointly connected switching communication networks which may not necessarily be undirected.As a direct application of this observer,we will further synthesize a distributed control law to solve the cooperative outputregulation problem ofa linearmulti-agentsystem subject to jointly connected switching communication networks.It is noted that the cooperative output regulation problem of a linear multi-agent system subject to jointly connected and undirected switching communication networks was also studied in[15].However,the system in this paper is somehow different from the one in[15]and the proof here is more straightforward and self-contained.

The rest of this paper is organized as follows.In Section 2,we establish a stability result for a class of linear switched systems.In Section 3,we present an outputbased distributed observerfora leadersystem subjectto jointly connected switching communication networks.In Section 4,we solve the cooperative output regulation problem of a linear multi-agent system subject to jointly connected switching communication networks via the output-based distributed observer approach.A numerical example is used to illustrate our design in Section 5,and the paper is closed in Section 6 with some concluding remarks.

Notation ⊗denotes the Kronecker product of matrices.‖x‖denotes the Euclidean norm of a vector x and ‖A‖denotes the induced norm of a matrix A by the Euclidean norm. λmax(A)and λmin(A)denote the maximum and the minimum eigenvalues of a symmetric matrix A,respectively.For xi∈Rni,i=1,...,m,col(x1,...,xm)=[xT1···xTm]T.We call a time function σ :[0,∞) → P={1,2,...,ρ},where ρ is some positive integer,a piecewise constant switching signal,if there exists a sequence{tj,j=0,1,2,...}satisfying t0=0,tj+1-tj? τ for some positive constant τ such that,for all t∈ [tj,tj+1),σ(t)=p for some p∈ P.P is called the switching index set,tjis called the switching instant,and τ is called the dwell time.

2 An extended stability result

In this section,we study the stability property of the following class of linear switched systems:

where x(t)∈ RNnis the state,S ∈ Rn×nand C ∈ Rm×nare constant matrices,and the pair(C,S)is observable;L ∈ Rn×mis a gain matrix to be designed;σ :[0,∞)→P={1,2,...,ρ}for some positive integer ρ,is a piecewise constant switching signal with switching instants{tj:j=0,1,2,...}and dwell time τ ＞ 0;Hσ(t)∈ RN×Nis a switching matrix dictated by the switching signal σ(t).

The stability property of a system similar to system(1)was first studied in[14]assuming that Hσ(t)is symmetric and positive semi-definite for all t?0.Later,the symmetry assumption on Hσ(t)was relaxed to the assumption[16,Assumption 3.2]that,for all p=1,...,ρ,the matrices HTp+Hp-μHTpHpare positive semi-definite for someμ＞0.It is clear that Assumption 3.2 of[16]is satisfied automatically if,for all p=1,...,ρ,the matrices Hpare symmetric and positive semi-definite.In what follows,we will further relax Assumption 3.2 of[16]to the following one.

Assumption 1 There exist aμ＞0 and a symmetric and positive definite matrix Q such that,for all p=1,...,ρ,the matrix HTpQ+QHp-μHTpQHpispositive semi-definite.

Also,like in[14],we assume the following one.

Assumption 2 The matrix S is neutrally stable,i.e.,all the eigenvalues of S are semi-simple with zero real parts.

Remark 1 Assumption 1 is motivated from the recentresultin[17],which studied the consensus problem ofa discrete-time linearmulti-agentsystem subjectto directed and jointly connected switching communication networks.As pointed out in[17],what makes Assumption 1 interesting is that it can be satisfied in some cases

where Assumption 3.2 of[16]is not satisfied.This point will be further illustrated with an example in Section 5.Under Assumption 2,there exists a symmetric and positive definite matrix P such that

Before establishing the stability property of system(1),we introduce the following result.

Lemma 1(Lemma 4 of[14]) Given a strictly increasing sequence{tj:j=0,1,2,...}with t0=0 andConsider the following system:

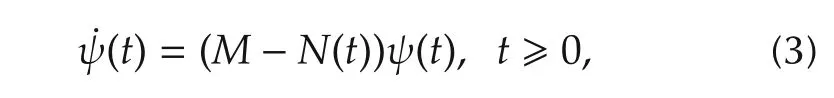
where M is a constant matrix,N(t)is bounded over[0,∞)and is constant over each time interval[tj,tj+1),j=0,1,2,....Suppose the solution ψ(t)of system(3)is bounded over[0,∞)and satisfies

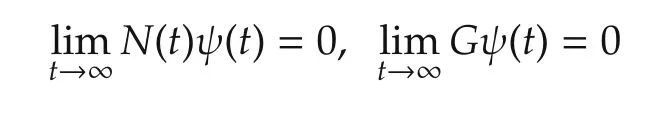
for some constant matrix G.Then

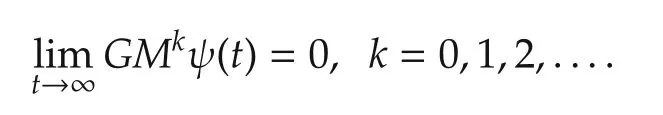
The following result can be viewed as an extension of the partial result of Theorem 1 in[14].

Lemma 2 Under Assumptions 1 and 2,suppose there exists a subsequence{jk:k=0,1,2,...}of{j:j=0,1,2,...}with tjk+1-tjk＜T for some T＞0,such that the matrixis nonsingular.Then,with L=P-1CT,the origin of system(1)is asymptotically stable.

Proof First note that(2)implies that

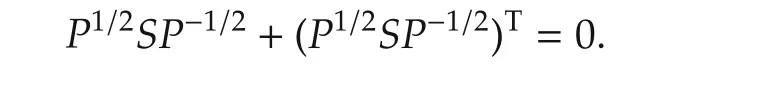
Then,with L=P-1CTand ξ(t)=(IN⊗ P1/2)x(t),system(1)is equivalent to

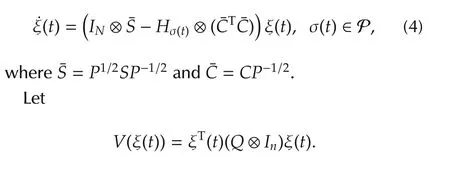
The time derivative of V(ξ(t))along the trajectory of system(4)exists on every time interval[tj,tj+1),j=0,1,2,...,and is given by

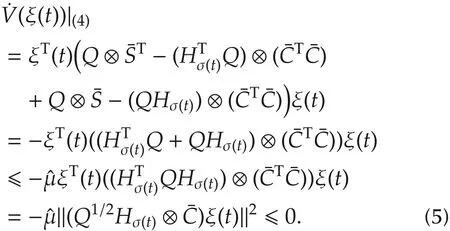
Thus,we have V(ξ(t))?V(ξ(0))for all t?0,and hence0.Moreover,

Since σ(t) ∈ P and P is a finite set,Hσ(t)is bounded over[0,∞).Then,by(4),˙ξ(t)is bounded over[0,∞)and so is¨V(ξ(t)).Therefore,by Corollary 1 of[14],and it follows from(5)that

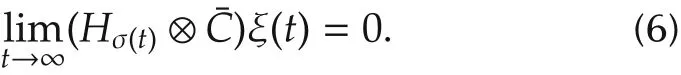
Similar to the proof of Theorem 1 in[14],we show that the origin of system(1)with L=P-1C is asymptotically stable by the following three steps.

Step 1 Let η(t)=(Hσ(t)⊗ In)ξ(t).We first show that(6)implies

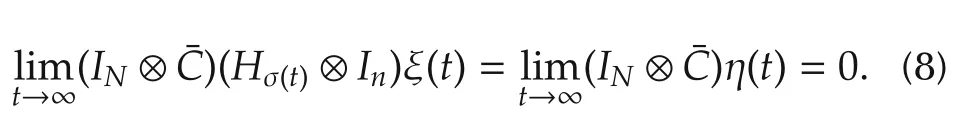
For this purpose,we note that(6)implies that

Since ξ(t)is bounded over[0,∞),η(t)is also bounded over[0,∞).Moreover,the derivative of η(t)exists on every time interval[tj,tj+1),j=0,1,2,...,and is given by

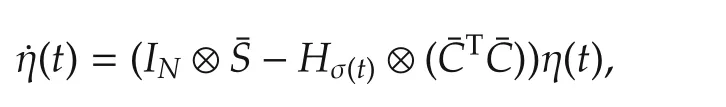
which is in the form of(3)with ψ(t)= η(t)and

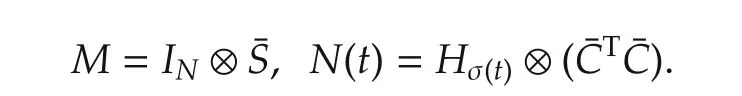
Let G=IN⊗C.Then,(6)and(8)imply

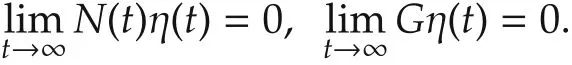
By Lemma 1,we have

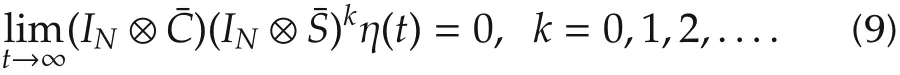
Note that the observability of the pair(C,S)implies the observability of the pair(C,S),and hence the observability of the pair(IN⊗C,IN⊗S).Therefore,from(9),we have=0,i.e.,equation(7)holds.

Step 2 Next,we further show that(7)implies

for any finite T0?0.

From(4),we have,for any t?0,

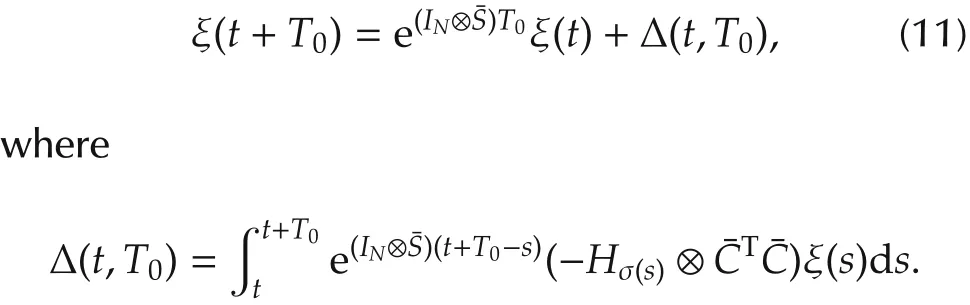
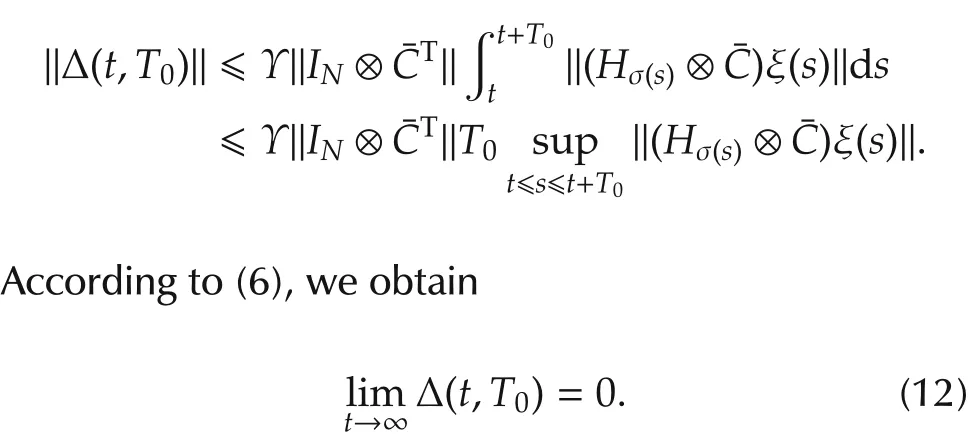
Thus,by(7),(11),(12),and the fact that Hσ(t+T0)⊗ Inis bounded over[0,∞),we have

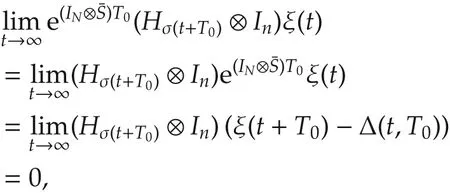
which gives(10)by noting that the matrix e(IN⊗S)T0is nonsingular for any T0?0.

Step 3 Finally,we show that the origin of system(1)is asymptotically stable with L=P-1C.

Letting t=tjkand t+T0=trfor r=jk,jk+1,...,jk+1-1,in(10)gives

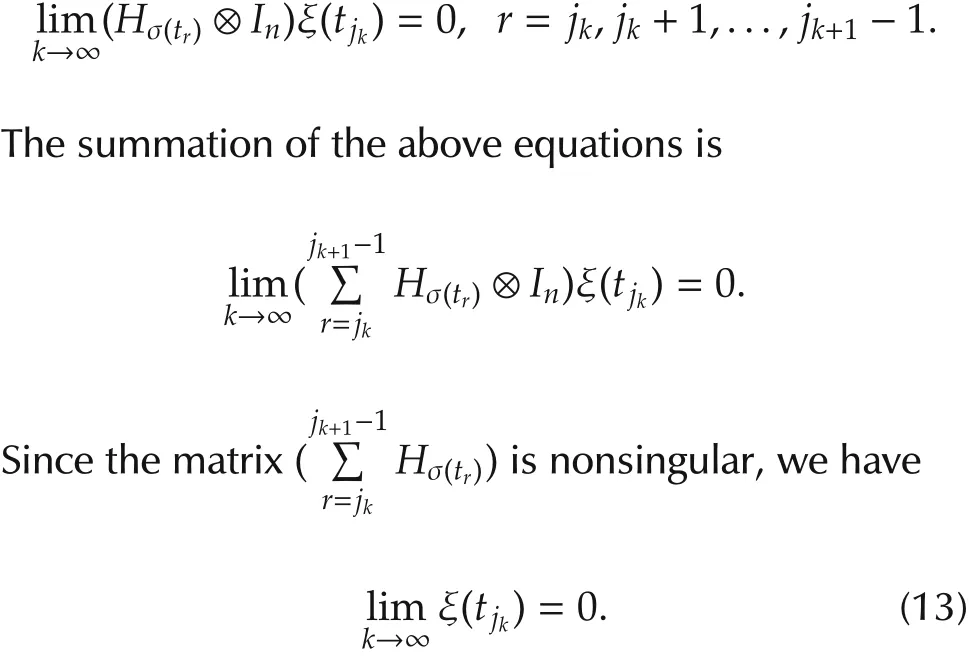
According to(5), ‖(Q1/2⊗ In)ξ(t)‖is non-increasing over[0,∞).This fact together with(13)concludes thatand therefore

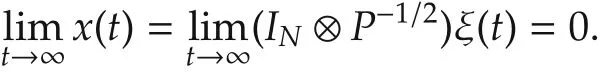
Thus,the proof is completed.

Remark 2 Lemma 2 can be viewed as a continuoustime counterpart of Lemma 2 of[17],which gave a stability result for a class of linear discrete-time switched systems.

3 An output-based distributed observer

In this section,we propose an output-based distributed observer for the leader system described by the following linear system:

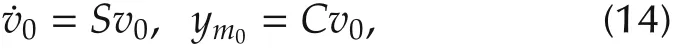
where v0∈Rn,ym0∈Rmare the state and the output,S ∈ Rn×nand C ∈ Rm×nare constant matrices,and the pair(C,S)is observable.

Assumption 3 There exists a subsequence{jk:k=0,1,2,...}of{j:j=0,1,2,...}with tjk+1-tjk＜T for some T＞0,such that the union digraphthe property that there is a directed path from node 0 to every other node.

Remark 3 Assumption 3 is called the jointly connected condition[18].Itisperhapsthe mildestcondition on the switching digraphGσ(t)as it allows the digraph to be disconnected at every time instant.

Given system(14)and the switching digraphGσ(t),as in[15],we denote bythe weighted adjacency matrix ofand define a distributed dynamic compensator as follows:

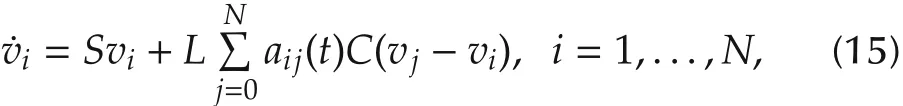
where L ∈ Rn×mis a gain matrix to be designed,and,for i=1,...,N,vi∈Rn.It can be seen that(15)depends on Cv0=ym0instead of v0.If there exists L such that,for any initial condition vi(0),i=0,1,...,N,the solutions of systems(14)and(15)exist for all t?0 and satisfy asymptotically,then system(15)is called an outputbased distributed observer for the leader system(14).

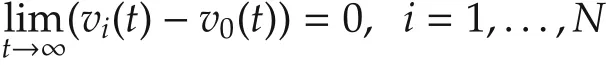
In the special case where C=In,we can take L=μInwith μ a positive constant.Then,(15)reduces to

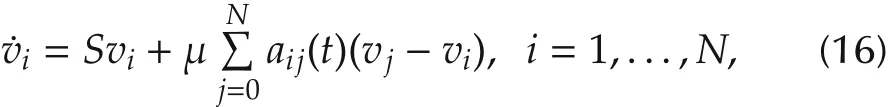
which was proposed in[11].By Lemma 2 and Remark 4 of[11],under Assumption 3 and the assumption thatthe matrix S has no eigenvalues with positive real parts,for any μ＞0 and any initial condition vi(0),i=0,1,...,N,the solutions of systems(14)and(16)exist for all t?0 and satisfy

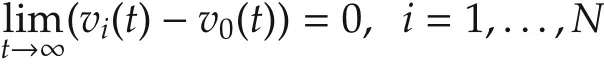
exponentially.For this reason,system(16)is called a(state-based)distributed observer for the leader system(14).

Now,letvi=vi-v0,i=1,...,N,andv=col(v1,...,vN).Then,system(15)can be compactly written as

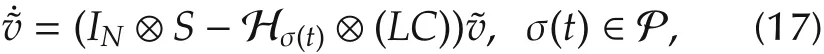
where,withLσ(t)∈R(N+1)×(N+1)denoting the Laplacian ofGσ(t),the matrix Hσ(t)∈RN×Nis obtained fromLσ(t)by removing the first row and the first column.

In order to apply Lemma 2 to show that(15)is indeed an output-based distributed observer for the leader system(14),we need to make one more assumption as follows.

Assumption 4 There exist aμ＞0 and a symmetric and positive definite matrix Q such that,for all p=1,...,ρ,the matrix HTpQ+Q Hp-μHTpQ Hpis positive semi-definite.

We are now ready to present the following result.

Lemma 3 Given systems(14)and(15),under Assumptions 2-4,for any initial conditions vi(0),i=0,1,...,N,the solutions of systems(14)and(15)with L=P-1CT,where P is the symmetric and positive definite solution to(2),exist for all t?0 and satisfy

Proof By the same argument as used in Remark 14 of[14],under Assumption 3,the matrixnonsingular.By Lemma 2,system(17)is asymptotically stable with L=P-1CT.Thus,the proofis completed.

4 An application

In this section,we apply the output-based distributed observer to solve the cooperative output regulation problem of the following class of linear multi-agent systems:

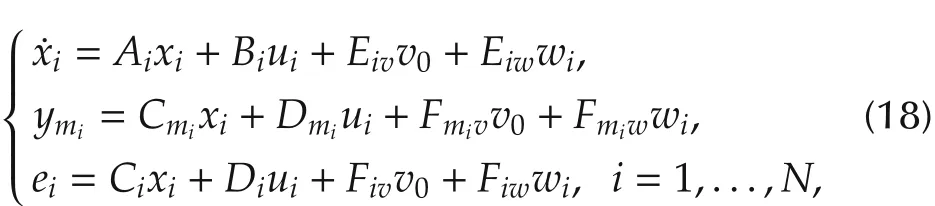
where,for i=1,...,N,xi∈Rni,ymi∈Rpmi,ei∈Rpi,and ui∈Rmiare the state,measurement output,error output,and control input of the i th subsystem,respectively;v0∈Rnis the measurable exogenous signal such as the reference input to be tracked,and it is assumed to be generated by(14);wi∈Rqiis the unmeasurable exogenous signal such as local external disturbances to each subsystem,and it is assumed to be generated by

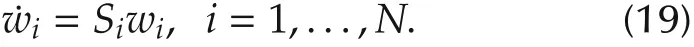
In practice,the communication among system(14)and different subsystems of(18)is subject to some constraints due to,say,the physical distance among them.In particular,the output signal ym0of system(14)may not be available for the control uiof all subsystems of(18).To describe the communication constraints among various subsystems,as in[11],we view the system composed of(14)and(18)as a multi-agent system with(14)as the leader and the N subsystems of(18)as followers.Then,given a piecewise constant switching signal σ(t),we can define a switching digraphGσ(t)=(V,ℰσ(t))whereV={0,1,...,N}.We associate node 0 with the leader system(14)and node i,i=1,...,N,with the i th follower subsystem of(18).The edge setℰσ(t)⊆V×V describes the communication constraints:for i=1,...,N,j=0,1,...,N,(j,i)∈ℰσ(t)if and only if uican use the information of agent j for control at time instant t.

We describe our control law as follows:

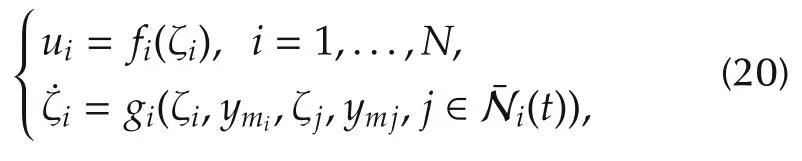
where,for i=1,...,N,Ni(t)={j∈V|(j,i)∈ℰσ(t)}is the neighbor set of node i at time t,both fi(·)and gi(·)are linear functions in their arguments,and ζiis the state of the dynamic compensator.In particular,it can be seen that,at each time instant t?0,uican make use of ym0if and only if the leader is a neighbor of the i th follower,or mathematically,0∈Ni(t).Such a control law is called a distributed control law.

We are now ready to describe the cooperative linear output regulation problem.

Problem description Given systems(14),(18),(19),and a switching digraphGσ(t),design a distributed control law of the form(20)such that,for any initial conditions v0(0),xi(0),wi(0),and ζi(0),i=1,...,N,the solution of the closed-loop system exists for all t?0 and satisfies

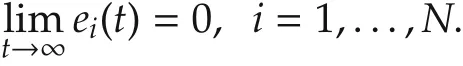
Some standard assumptions for solving the above problem are listed below.

Assumption 5 For i=1,...,N,the pairs(Ai,Bi)are stabilizable.

Assumption 6 For i=1,...,N,the pairs

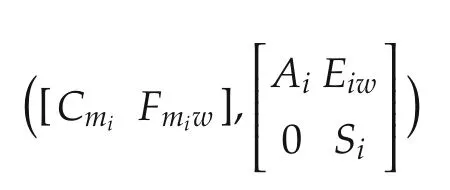
are detectable.

To introduce the next assumption,letEi=[EivEiw],and Fi=[FivFiw].

Assumption 7 For i=1,...,N,the linear matrix equations

have solution pairs(Xi,Ui).

Remark 4 Assumptions 5-7 are standard as they have been used in both the classicallinearoutputregulation problem[19-21]and the cooperative linear output regulation problem[11,15]by a measurement output feedback control law.In particular,equations in(21)are called the regulator equations,whose solvability imposes a necessary condition for the solvability of the(cooperative)linear output regulation problem.

To motivate our approach,we assume,tentatively,that every follower subsystem of(18)can access the state v0of the leader system(14).In this case,it is possible to find a so-called purely decentralized control law to solve our problem.

For i=1,...,N,under Assumption 5,there exists K1i∈ Rmi×nisuch that Ai+BiK1iis Hurwitz.Under Assumption 7,let(Xi,Ui)be a solution pairto the regulator equations in(21),define K2i=Ui-K1iXi∈ Rmi×(n+qi),and further partition K2ias K2i=[K2ivK2iw]with K2iv∈ Rmi×nand K2iw∈ Rmi×qi.Moreover,under Assumption 6,there exists Li∈ R(ni+qi)×pmi such that

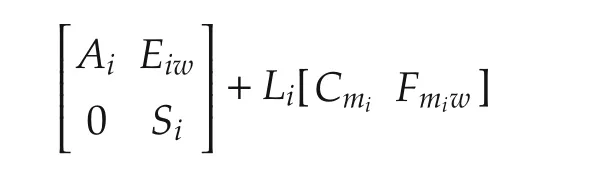
is Hurwitz.Then,it can be shown,as in the classical linear output regulation theory[19-21],that the following dynamic measurement output feedback control law solves our problem:

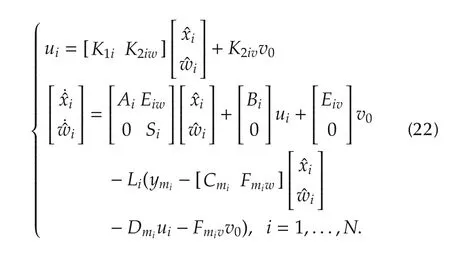
Nevertheless,the control law(22)is not in the form of(20)since,for each i=1,...,N,the control uihas to rely on the state v0of the leader system(14).We call such a control law a purely decentralized control law.To obtain a distributed control of the form(20),composing the purely decentralized control law(22)and the output-based distributed observer(15)yields the following control law:

Remark 5 It can be seen that the first two equations of(23)are obtained from(22)by replacing v0with vi,i=1,...,N,which are provided by the third equation of(23).This way of synthesizing a control law is known as the certainty equivalence principle.Moreover,it is noted that(23)is in the form of(20)with ζi=col(xi,wi,vi),i=1,...,N.

Theorem 1 UnderAssumptions 2-7,the distributed dynamic measurement output feedback control law(23)solves the cooperative output regulation problem of the system composed of(14),(18),and(19).

Proof For i=1,...,N,let

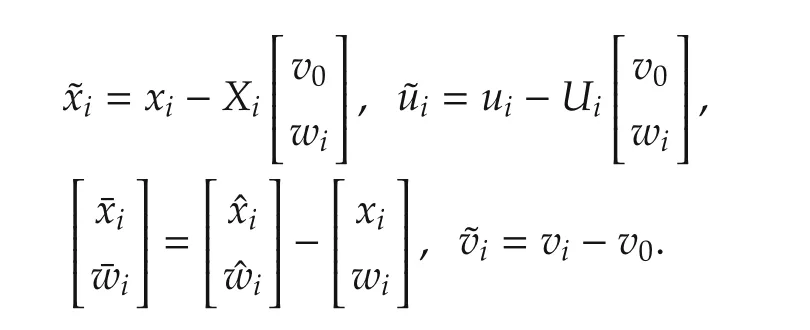
Under Assumption 7,by making use of the solution to the regulatorequations in(21),we have,for i=1,...,N,

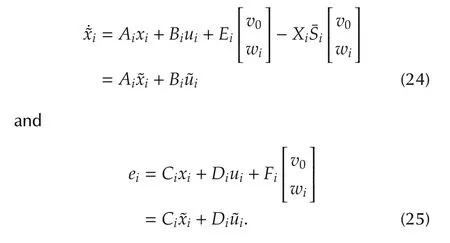
According to our control law(23),we have,for i=1,...,N,

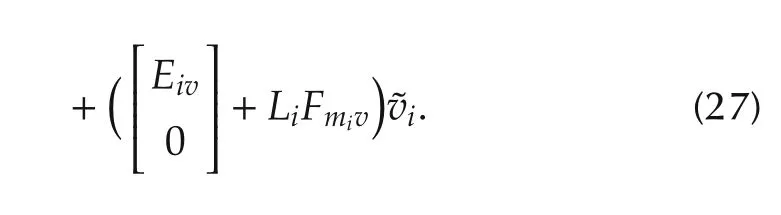
We first note that,by Lemma 3,under Assumptions 2-4,=0,i=1,...,N.Furthermore,under Assumption 6,system(27)is a strictly stable linear timeinvariant system subject to an asymptotically decaying input.Thus,we have

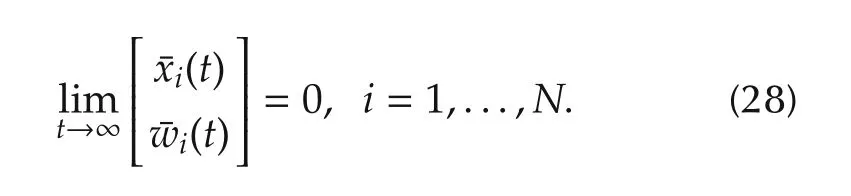
Next,substituting(26)into(24)yields

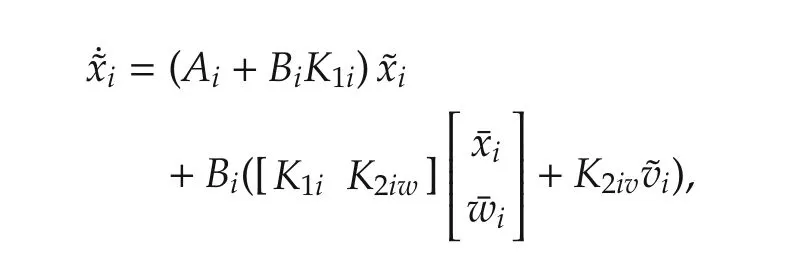
which again,under Assumption 5,can be viewed as a strictly stable linear time-invariant system subject to an asymptotically decaying input.Thus,we have

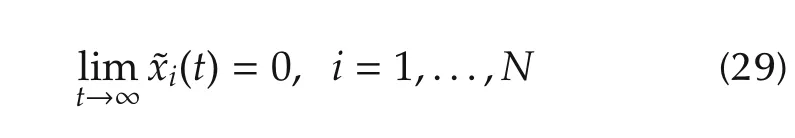
and therefore by(25),(26),(28),and(29),

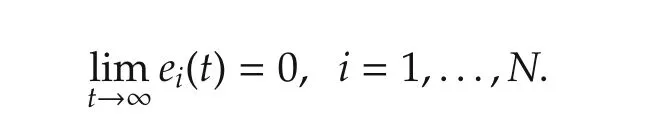
5 An example

In this section,we present an example to illustrate our design.Consider the cooperative output regulation problem for a group of double integrator systems subject to local sinusoidal disturbances:

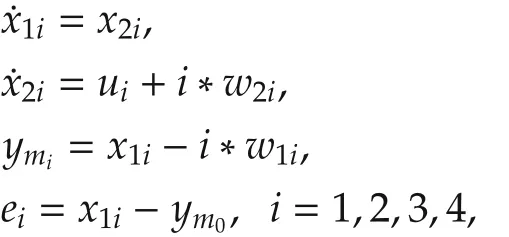
where the local disturbance wi=col(w1i,w2i)to each subsystem is generated by and the reference signal ym0is generated by the following leader system:

For this example,N=4 and

It is easy to check that Assumptions 2 and 5-7 hold.In particular,the regulator equations in(21)admit the following solutions:

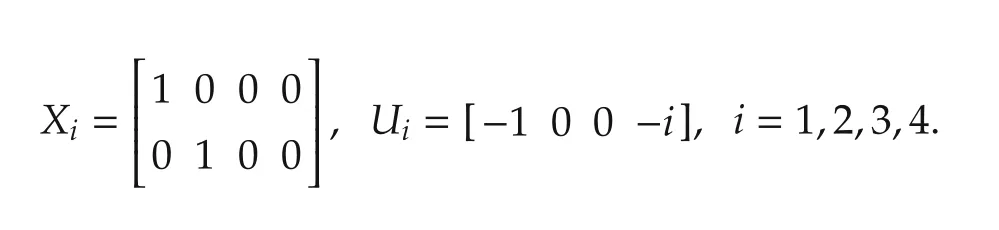
Assume that the switching digraphGσ(t)is dictated by the following switching signal:

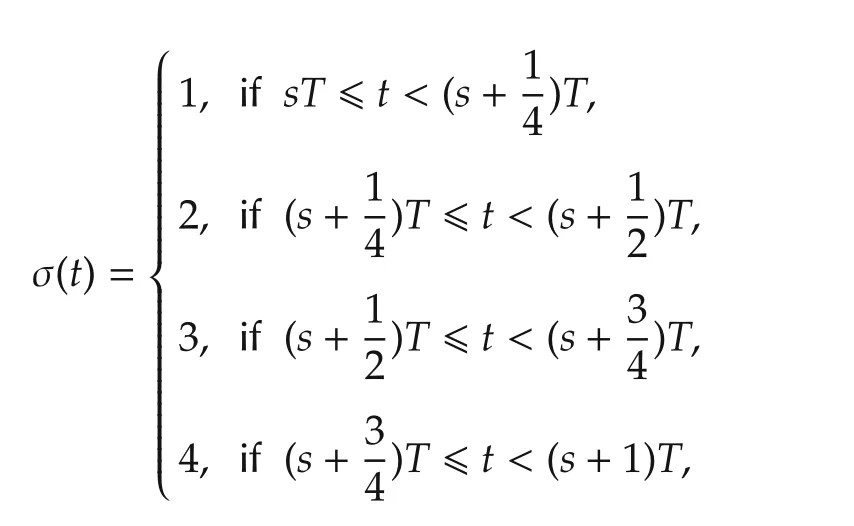
where T=2 and s=0,1,2,....The four digraphs,i=1,2,3,4,are described in Fig.1,where node 0 is associated with the leader system and the other four nodes are associated with the four follower subsystems.It can be seen that Assumption 3 is satisfied even thoughσ(t)is disconnected for all t?0.

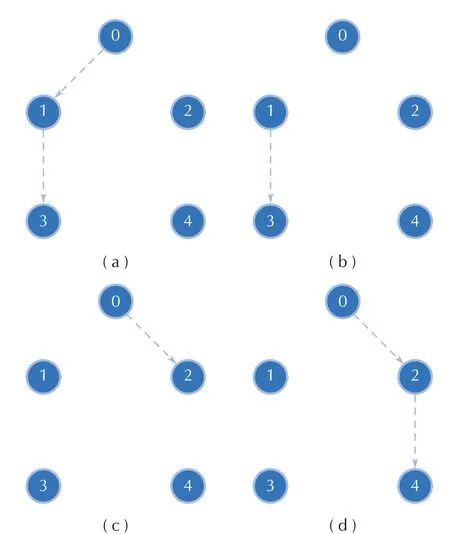
Fig.1 Switching topologywith P={1,2,3,4}

Let aij(t)=1,i,j=0,1,2,3,4,whenever(j,i)∈Then,the fourmatrices associated with the fourdigraphs,i=1,2,3,4,are given as follows:

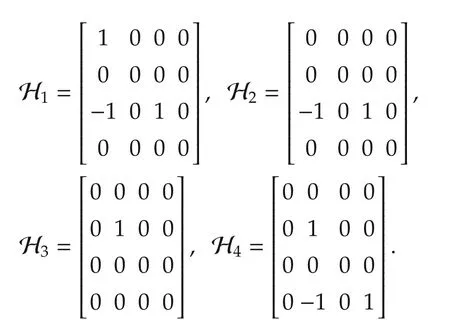
Clearly,none of the matrices Hi,i=1,2,3,4,are symmetric.Moreover,there exists noμ＞0 such that the matrix HT2+H2-μHT2H2ispositive semi-definite.Thus,for this example,Assumption 3.2 of[16]cannot be satisfied.However,let

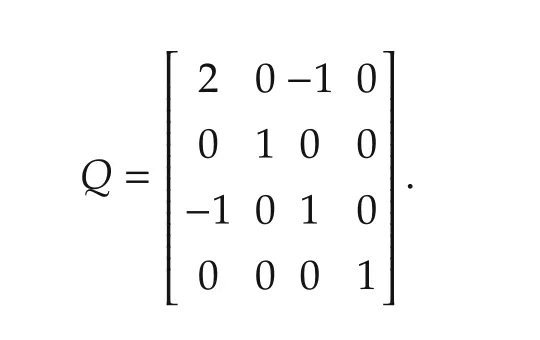
Then,it can be verified that,for i=1,2,3,4are positive semi-definite forμ?1.Thus,Assumption 4 is satisfied.

By Theorem 1,we can design a distributed dynamic measurement output feedback control law of the form(23)with the following design parameters:K1i=[-8-4],K2i=[7 4 0-i],i=1,2,3,4,L1=[-51-68-37 3]T,L2=[-13-12 0 6]T,L3=[-6-4 3 2]T,L4=[-3-2 3 0]T,and L=CT.

Simulation of the closed-loop system is performed with randomly generated initial conditions.Fig.2 shows the evolution of the estimation errors of the outputbased distributed observer and Fig.3 shows the evolution of the error outputs of the followers.

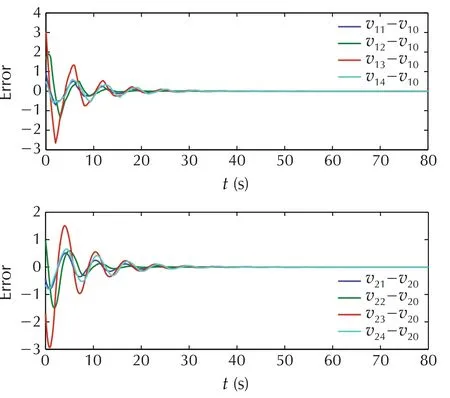
Fig.2 Profile on the estimation errors on the leader’s state v0.

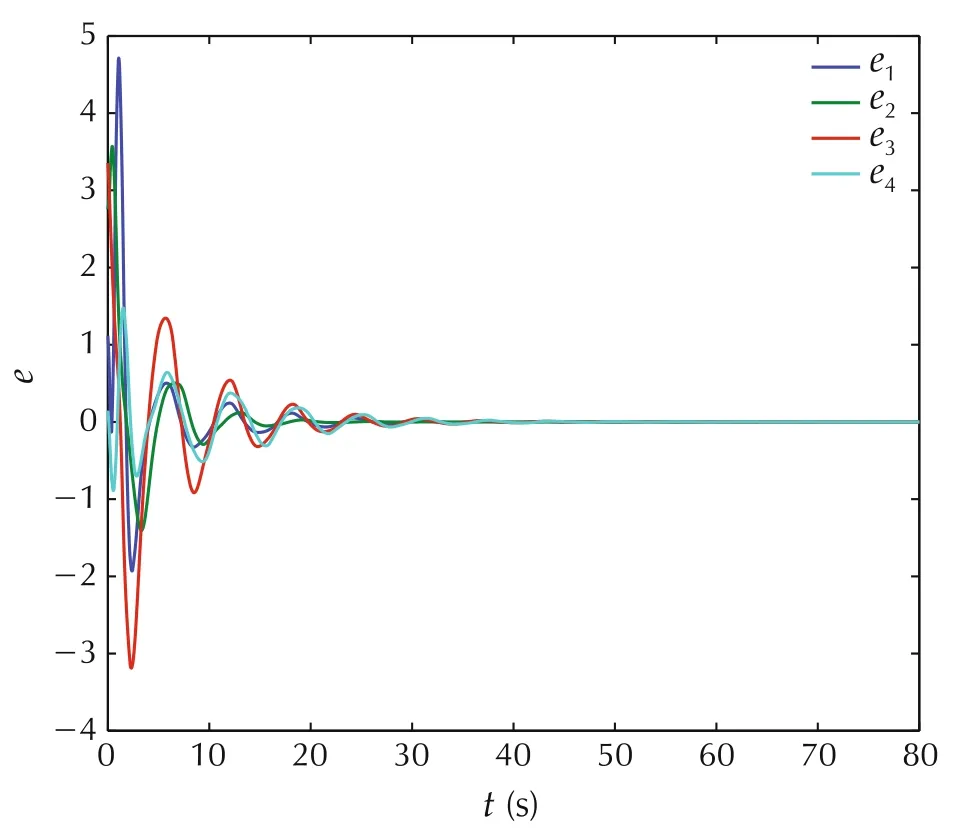
Fig.3 Profile on the error outputs of the followers.

6 Conclusions

In this paper,we have extended a stability result for a class of linear switched systems,which,in turn,has led to an output-based distributed observer subject to directed and jointly connected switching communication networks.As an application of this output-based distributed observer,we have solved the cooperative output regulation problem of a linear multi-agent system subject to jointly connected switching communication networks.It is also possible to apply the outputbased distributed observer to the leader-following attitude consensus problem of multiple rigid spacecraft systems studied in[4]and the leader-following consensus problem of multiple Euler-Lagrange systems studied in[12].

Appendix

A digraph G=(V,ℰ)consists of a finite set of nodes V={1,...,N}and an edge set ℰ ⊆ V × V.An edge of ℰfrom node i to node j is denoted by(i,j)and node i is called a neighbor of node j.Let Ni={j∈ V|(j,i)∈ ℰ}.Then,Niis called the neighbor set of node i.The edge(i,j)is called undirected if(i,j)∈ℰ implies(j,i)∈ℰ.The digraph G is undirected if every edge in ℰ is undirected.If the digraph contains a set of edges of the form{(i1,i2),(i2,i3),...,(ik-1,ik)},then this set is called a directed path of G from node i1to node ik.Given a set of ρ digraphs Gi=(V,ℰi),i=1,...,ρ,the digraph G=(V,ℰ)withis called the union of the digraphs Giand is denoted by

The weighted adjacency matrix of a digraph G is a nonnegative matrixwhere aii=0 and aij＞ 0 if and only if(j,i)∈ ℰ.The Laplacian of G is then defined as

Given a piecewise constant switching signal σ(t),and a set of digraphs Gi=(V,ℰi),i=1,...,ρ,with the corresponding weighted adjacency matrices denoted by Ai,i=1,...,ρ,we call the time-varying digraph Gσ(t)=(V,ℰσ(t))a switching digraph and denote the weighted adjacency matrix and the Laplacian of Gσ(t)by Aσ(t)and Lσ(t),respectively.