Prediction method for energy consumption per ton of fused magnesium furnaces using data driven and mechanism model

Dan GUO ,Zhiwei WU ,2†,Tianyou CHAI,2,Jie YANG ,Jinliang DING ,2

1.State Key Laboratory of Synthetical Automation for Process Industries,Northeastern University,Shenyang Liaoning 110819,China;

2.National Engineering Research Center of Metallurgical Automation(Shenyang),Shenyang Liaoning 110819,China

Received 5 September 2018;revised 4 October 2018;accepted 8 October 2018

Abstract The electric energy consumed in every ton of acceptable product,namely energy consumption per ton(ECT),is an important overall index for the production process of a fused magnesium furnace.The furnace is the equipment for producing the fused magnesia.The ECT value depends on the current in the smelting process.The optimal operation for a fused magnesium furnace is supposed to have the ECT as low as possible,where the key is to predict ECT accurately.By introducing an unknown high-order nonlinear term,this paper builds a dynamic ECT model for different production batches based on the static ECT model for one batch.The average current is taken as the input of the dynamic ECT model,which is composed of the unknown high-order nonlinear term and a nonlinear model with unknown parameters.The order of the nonlinear term is determined by the distance correlation and the nonlinear term is estimated by the stochastic configuration network,while the parameters of the nonlinear model is identified by the least square method.The estimation of the nonlinear term alternates with the parameter identification.This paper proposes a prediction method for ECT,which is composed of the order identification of the nonlinear term,the alternating identification of the model and the ECT prediction model.The simulation experiments are conducted by the on-site data,and the results verify the effectiveness of the proposed prediction method.

Keywords:Fused magnesia,energy consumption per ton,alternating identification,stochastic configuration network,distance correlation

1 Introduction

The fused magnesia is a kind of high-purified crystal MgO,and it is the main raw material of refractory in the fields of aerospace industry and manufacturing industry because of its good characteristics,such as a high melting point,anti-oxidation,good electric insulation,structural integrity and so on.The equipment for producing the fused magnesia is the three-phase alternating current fused magnesium furnace.The smelting temperature for the fused magnesia is higher than that for the steel-making,and it is as high as about 3000 degrees Celsius.The fused magnesium furnace is different from the electric-arc furnace for steel-making,and it is a kind of submerged arc furnace where the three-phase electrodes are buried in the raw material and the electric arcs are developed among the raw material and threephase electrodes[1].The raw material is heated by the electric arcs,and the molten pool is formed in the furnace.After the molten liquid cooling down naturally and crystallizes,the fused magnesia product will be got[2].

The fused magnesium furnace is a type ofhigh energyconsuming facilities,and the cost of electric energy accounts for more than 60 percent of the whole cost in the magnesia production.Lowering the electricity cost and raising the electric energy efficiency have become the major issues for the magnesia enterprises[3].The overall index for the production process of a fused magnesium furnace is the electric energy consumed in every ton of acceptable product,namely the energy consumption per ton(ECT),which can reflect the electric energy efficiency in the smelting[4].The electric energy consumed in one batch depends on the average current in the smelting process because the voltage and the production time change slightly in different batches.There is a close relationship between ECT and the current:If the current is too low,the raw material will not be melted completely and the yield of the acceptable product will be low,so the ECT value will be high;If the current is too high,the electric energy will be wasted as there is an upper limit for the yield in one batch,so the ECT value will also be high[5].As a result,the optimum current corresponds to the lowest ECT.The aim of the optimal operation for a fused magnesia furnace is to have the ECT as low as possible under the demand constraint[6].Thus,an accurate ECT prediction model is helpful to decide the optimum current and to lower the ECT value.

In recent years,the hybird modeling approaches based on models and data have become the hotspot in the modeling of industrial process:The known dynamic properties of the complex system are described by the mechanism models,while the dynamic properties that are not included in the models are described by the collected data[7].Since wastewater treatment plants are cascaded processes,the mechanism model is connected with the hierarchical neural networks,and the combination of the model and the neural networks provide water quality in inner reactors[8].To accurately predict the matte grade in copper flash smelting process,a self-adaptive combination technology is adopted to integrate the mathematic model and a fuzzy neural network[9].Three kinetic models of p-xylene oxidation process are studied in[10],and then a comparative study of the six hybrid models combining kinetic and regression module parts is carried out.A hybrid modeling approach for centrifugal compressor is proposed,and the hybrid models consist of a three-layer artificial neural network and a mechanistic component[11].An assumption in the above studies isthatthe parametersof the mechanism models are fixed and changeless.In the production of the fused magnesia,however,the ingredient and the particle size of the raw material fluctuate frequently,and the parameters within the furnace are uncertain and undetectable,like the arc length,the resistance of the molten pool.As a result,it is hard for the above methods to obtain an accurate ECT prediction model.The mechanism prediction model of ECT for one production batch has been constructed by the principle of the conservation of energy[12].However,the ECT prediction model is of low quality,and there are some reasons.Above all,the parameters of the mechanism model are considered as the constants and they are chosen by the experience,but in fact these parameters are unknown nonlinear functions.In addition,the raw material,the operations and the loss of equipment change with production batches,which are not taken into account.Last but not the least,the ECT values for different production batches are assumed to be independent and irrelevant.Thus,both the correlation and the difference among different batches need to be considered for an accurate ECT prediction model.

The main motivation of this paper is to take advantage of the ECT mechanism model for one batch[12]to build an accurate dynamic ECT prediction model for different batches,and a prediction method for ECT is proposed.The main contributions of this paper are as follows:

1)A dynamic ECT model for different production batches is built,and the dynamic model is described by a nonlinear model with unknown parameters and an unknown high-order nonlinear term.

2)The nonlinear model is transformed into a model whose parameters can be identified.

3)A prediction method for ECT using data driven and mechanism model is proposed,which is composed of three parts,i.e.,the order identification of the nonlinear term,the alternating identification of the model and the ECT prediction model.

4)The simulation experiments are conducted by the on-site data,and the results demonstrate that the proposed prediction method can significantly improve the prediction accuracy of ECT.

The restofthis paperis organized as follows.Section 2 briefly introduces the production process of the fused magnesia.A dynamic ECT model for different production batches is built in Section 3.Section 4 provides the ECT prediction modeland the transformation ofthe nonlinear model for the identification of its parameters.The main components of our proposed prediction method are explained in Section 5.Section 6 presents the simulation results.Section 7 concludes this paper.

2 Production process of fused magnesia

A schematic diagram of the production process of the fused magnesia is illustrated in Fig.1,and the whole process in every batch lasts about 10 hours.The control system of the fused magnesium furnace is designed based on stable currents,and the manipulated variables are the currentsofthe three-phase electrodes.The transformer voltage fluctuates within a small range during the production,so the current value depends on the arc resistance which has a close relationship with the length of the arc.The control system of the fused magnesium furnace adjusts the distance between the electrodes and the surface of the molten pool by the positive-negative rotating of motors,so the currents of electrodes are able to follow the current setpoint[13].The arcs among electrodes and raw materials convert the electric energy to the thermal energy.Certain amount of caustic calcined magnesia powderwillbe charged to the furnace every 8-12 minutes,and the main reactions for caustic calcined magnesia are[14]

where equation(1)is the process of high-temperature calcination,and the product of high density is obtained,while equation(2)is the liquefaction process,and the product are purified.As the melting points of NaOH,CaO,Fe2O3are lower than that of MgO,these impurities will first melt and migrate out.The surface of the molten pool gradually raises with the charge and the fusion of the raw material.Power supply is cut off and the car is dragged away when the pool surface approaches to the furnace mouth.The liquid in the furnace crystallizes after a natural cooling,and then the crystal is broke and sorted for the final product.The ECT value of the furnace in one production batch will be finally counted based on the electric energy consumption and the yield of the acceptable product.

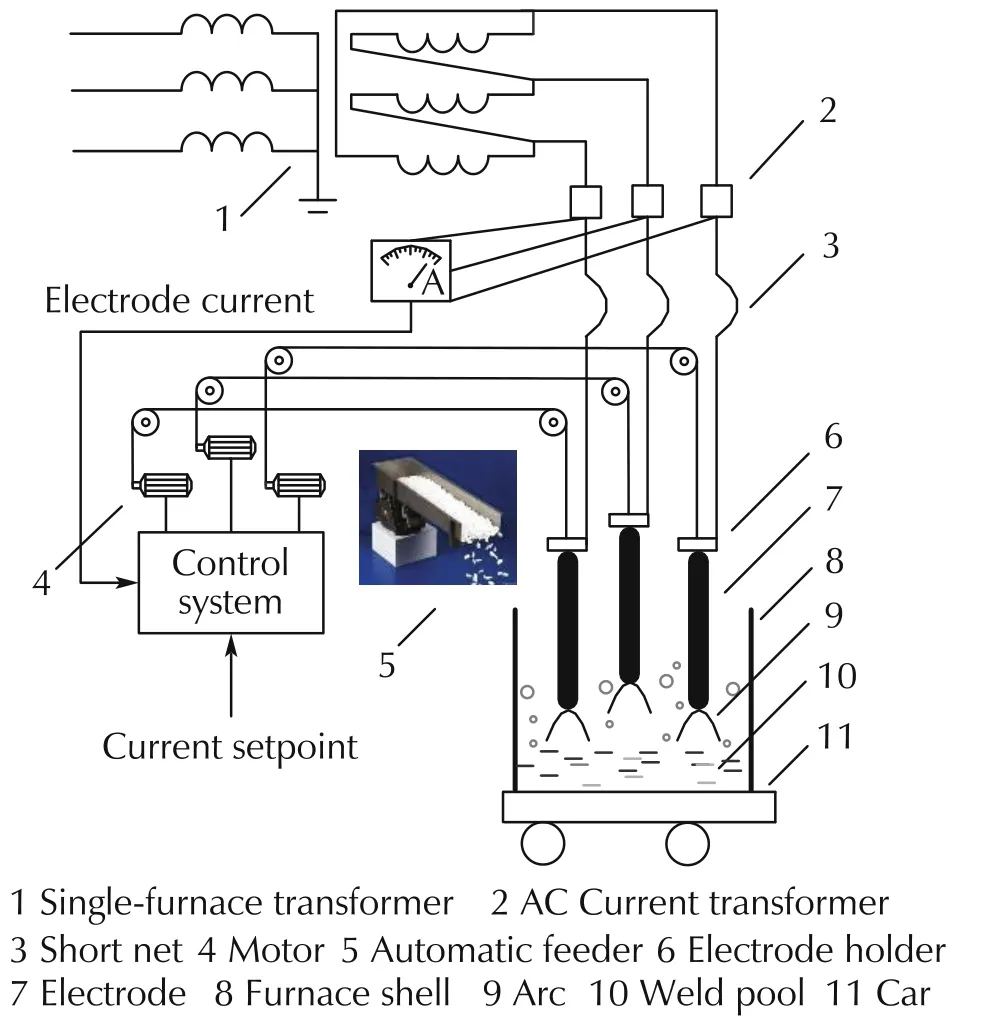
Fig.1 A schematic diagram of the production process of the fused magnesia.

Fig.2 shows the nonlinear relationship between the average current and ECT.The key to the optimal operation for a fused magnesia furnace is to build an accurate ECT prediction model.However,there are a few reasons why it is hard to build an accurate ECT model:First,there exist many physical and chemical processes in the production,such as calcination,fusion,impurity precipitation and crystallization;in addition,a blend of solid,liquid and gas in the environment of about 3000 degrees Celsius leads to the failure of all sensors,and it is unable to detect the parameters in the furnace,like the arc resistance,the depth of the molten pool;Last but not least,the raw material is charged intermittently,and the ingredient and the particle size of the raw material fluctuate,so the parameters inside the furnace change with time.

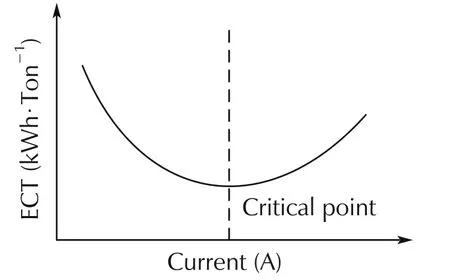
Fig.2 The nonlinear relationship between the average current and ECT.

3 Dynamic ECT model for different production batches

Taking the average current as the input,the mechanism model of ECT for one batch has been constructed by the principle of the conservation of energy[12],and it has the following expression:

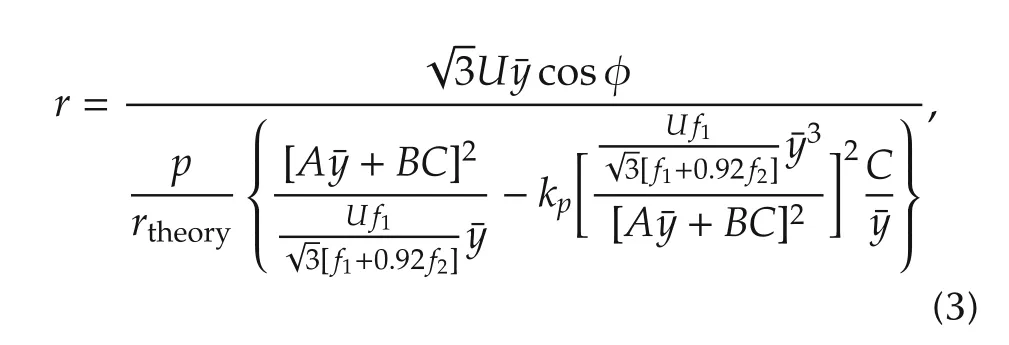
wherey is the average current in the smelting process,

where yminand ymaxare the lower limit and the upper limitforthe currentin the smelting process,respectively,and y(t)is the average current of the three electrodes at time t.The related parameters to the mechanism model(equation(3))and their meanings are listed in Table 1.

In[12],the parameters of the mechanism models are assumed to be fixed and changeless,so equation(3)is a static model.During one production batch,however,the parameters in Table 1 are acturally the unknown variables.One reason is that the ingredient and the particle size of the raw material fluctuate frequently.In addition,the powder raw material is charged by automatic feeder intermittently,and it is easy for the raw material to fall into the different regions because of the looseness of the powder and the motion of the electrodes,so the length and the resistance of the arcs change with the thickness of the material layer in the furnace.

Table 1 The list of the parameters in the ECT mechanism model.

Furthermore,the melting rate of raw material is related to the distance to the arcs,and the change of the melting rate will lead to the fluctuation of the resistance of the molten pool.Another reason is that there actually exist three loads because of three-phase electrodes,and the change of the arc resistance or the pool resistance in any phase will affect the currents of the three-phase electrodes,so there is a continuous fluctuation for the thermal loss of the power supply system and the overall thermal efficiency.Overall,the parameters in equation(3)are unknown nonlinear functions,so the accurate expression for equation(3)is

The above expression is the ECT model for just one production batch,and a ECT prediction model should be suitable for different batches.Considering that the raw material,the operations and so on change with batches,a nonlinear term Δr1(S)is introduced to represent the differences among different batches,so the ECT model for any batch S can be formulated as

The ECT values can not be calculated according to the above equation as the unknown variables are included,thus the unknown constants are used to replace the variables.The errors caused by the replacement is denoted as the unknown nonlinear term Δr2(S).Overall,the dynamic ECT model for different production batches can be expressed as

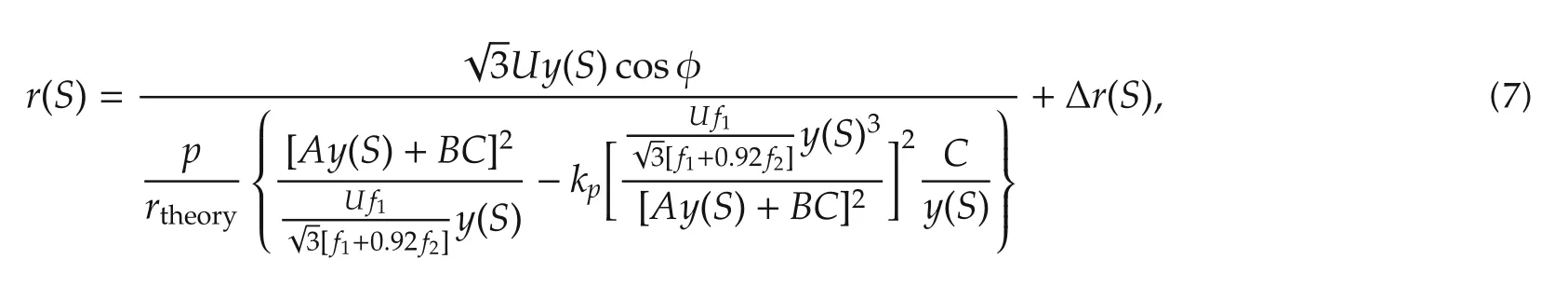
where the nonlinear term Δr(S)= Δr1(S)+Δr2(S).

4 Prediction model of ECT

4.1 ECT prediction model

The dynamic ECT model in equation(7)is composed of a nonlinear model with unknown parameters and an unknown high-order nonlinear term.If the nonlinear model is denoted asr(S),then

There is no big difference for some working conditions in two successive batches,for example,the loss of the equipment,so it is assumed that the ECT value of the(S+1)th batch has a close relationship with that of the S th batch,

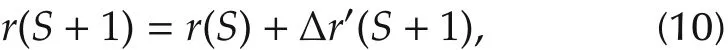
where the nonlinear term Δr′(S+1)represents the difference in ECT values between the two batches.Combining equation(9)and equation(10),the new equation is

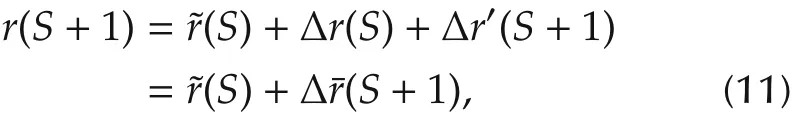
wherer(S)is derived from equation(8)and the highorder nonlinear term Δr(S+1)is unknown.As the parameters in equation(8)can not be detected,the estimationr(S)will be got based on the approximation of the parameters.Δr(S+1)is estimated based on the ECT and the average current in the previous production batches,that is Δr(S+1)=f(r(S),r(S-1),...,r(S-dr),y(S),y(S-1),...,y(S-dy)),where drand dyare unknown.Overall,the ECT prediction model is formulated as

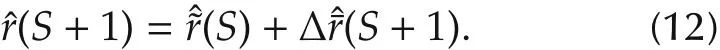
The parameters in equation(8)need to be identified before ECT is predicted based on equation(12),and thus the nonlinear model(equation(8))is supposed to be transformed into the model with the identifiable parameters.

4.2 Parameter identification in ECT prediction model

New variables F0∼F11is introduced to transform equation(8)into the model with the identifiable parameters,and the expressions for F0∼F11is in Table 2.The new equation based on F1∼F11is

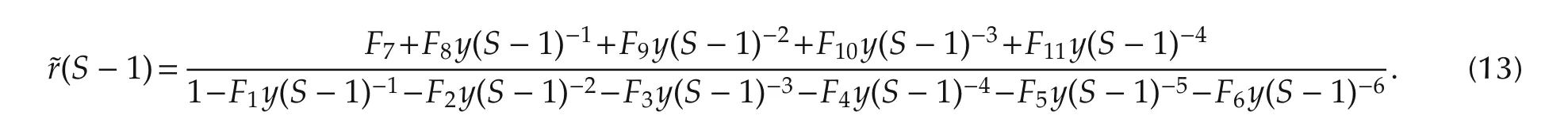
From equation(11),we can getr(S-1)=r(S)-Δr(S).r(S)-Δr(S)is made use of to replacer(S-1)in equation(13),and the equation for parameter identification finally is

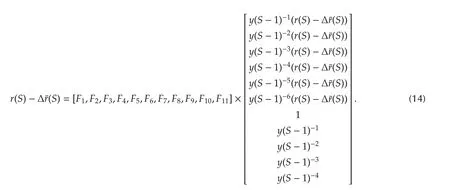
Table 2 The expressions for F0∼F11.

The nonlinear term Δr(S)needs to be known before equation(14)is applied to identify F1∼F11by the least square method,but F1∼F11also need to be known before Δr(S)is calculated according to equation(13)and equation(11),so Δr(S)and F1∼F11affect each other.

5 Prediction method of ECT

This paper proposes a prediction method based on the ECT prediction model(equation(12)),which is composed of the order identification of the nonlinear term,the alternating identification of the model and the ECT prediction model.The detailed ECT prediction strategies and algorithms will be described as follows.

5.1 Prediction strategy of ECT

As shown in Fig.3,the proposed structure diagram for the ECT prediction method is made up of three parts.

.Orderidentification ofthe nonlinear term drand dyare determined by the distance correlation method based on the collected data.dris the number of batches

where historical ECT values are related to the nonlinear term Δr(S+1),while dyis the number of batches where historical average currents are related to the nonlinear term.

.Alternating identification of the model The nonlinear term Δr(S+1)is estimated by the stochastic configuration network,and the parameters of the nonlinear model(equation(8))is identified by the least square method.The estimation of the nonlinear term alternates with the parameter identification.

.ECT prediction model The prediction value ofECT is calculated by equation(12)based on the average current y(S),the estimationsF1∼F11and Δr(S+1).

Fig.3 The structure diagram for the ECT prediction method.

5.2 Prediction algorithm of ECT

5.2.1 Order identification of nonlinear term

The distance correlation method suggested in[15]is applied to describe the degree of relevance between random variables.Both linear and nonlinear association can be measured by the distance correlation.The measurement of distance correlation is zero if and only if two random variables are independent.

It is assumed that there are N observations for two variables X(X=[x1,x2,...,xN]T)and Y(Y=[y1,y2,...,yN]T),and then two K×K matrices(A and B)are obtained by

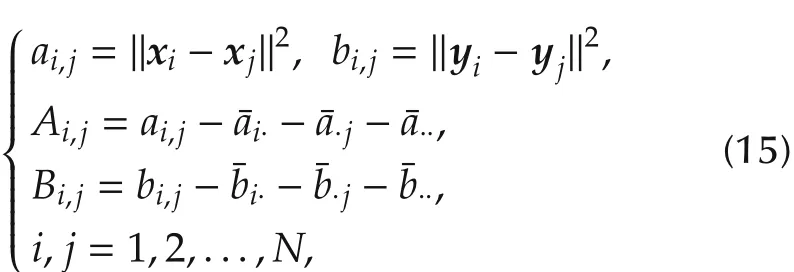
whereai·anda·jare the mean value of i th row and j th column respectively,anda··is the grand mean.A scalar(distance covariance)can be obtained by an average of the product of A and B

The association measurementof X and Y by the distance correlation method is

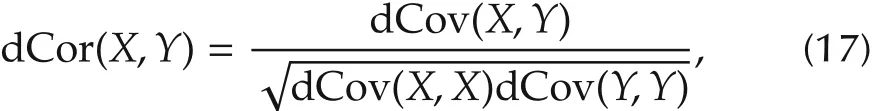
where the expressions for dCov(X,X)and dCov(Y,Y)can refer to equation(16).From the above,the steps to determine the orders drand dyare as follows(suppose that there are N sets of collected data):

1)According to the empirical value of the parameters[12],like the resistance of molten pool,voltage drop and so on,calculate the initial estimationsF1∼F11based on Table 2.

2)According to equation(13),equation(11)andestimate,...

3)Set dr=dy=0.

4)Measure the association between...,S-N+2+dr)]Tand[r(S-1-dr),r(S-2-dr),...,r(S-N+1)]Taccording to equations(15)-(17).If the distance correlation is smaller than the threshold valueδ,then dristhe numberofbatcheswhere historical ECT values are related to the nonlinear term,otherwise set dr=dr+1 and repeat step 3).

5)Measure the association between...,Δr(S-N+2+dy)]Tand[y(S-1-dy),y(S-2-dy),...,y(S-N+1)]Taccording to equations(15)∼(17).If the distance correlation is smaller than the threshold valueδ,then stop and dyis the numberofbatches where historical average currents are related to the nonlinear term,otherwise set dy=dy+1 and repeat step 4).

5.2.2 Alternating identification

.Estimation of nonlinear term

drand dyhave been determined by the distance correlation in the last section,so Δr(S+1)can be expressed by a nonlinear function fΔr(·)whose inputs are dr+dyvariables,that is

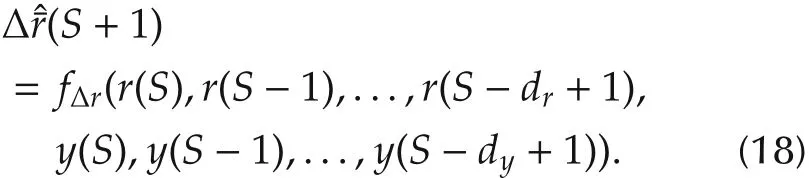
For the sake of brevity,let

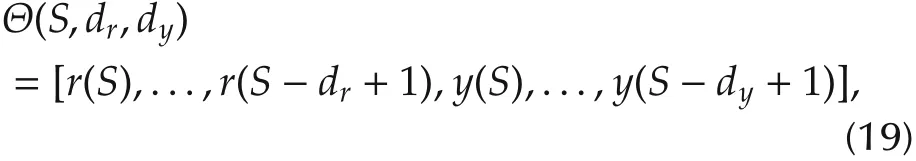
then equation(18)can be written as

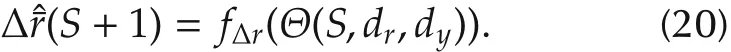
In this paper,the stochastic configuration network(SCN)[16,17]is used to estimate fΔr(·).Suppose that there are N sets of historical ECTs and average currents,that is[r(S),r(S-1),...,r(S-N+1)]and[y(S),y(S-1),...,y(S-N+1)],then the training data of SCN are

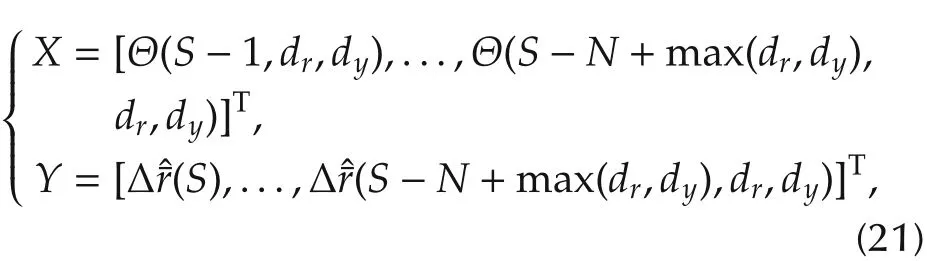
where X∈Rdr+dy,Y∈R,andmax(dr,dy),dr,dy)are derived from step 1)in Section 5.2.1.

The training of SCN is fast.In addition,SCN has a satisfied generalization ability even if there is no prior knowledge about the model complexity.Starting from a small-scale network,SCN adds the hidden neurons gradually until the stopping criterion is reached.It has been proved that SCN has the universal approximation property.

The training process of SCN is illustrated as Fig.4.SCN generates the initial weights and biases within a small range.If the generated weights and biases can not provide satisfied neurons,the range will be extended.The positive scalars Λ ={λmin:Δλ :λmax}are used to define the range of weights and biases.An increasing sequence Γ (γ ∈ Γ)is defined in SCN,and every element in Γ is smaller than 1 but approaches to 1.If no neurons satisfies the condition which is related to γ,the next element in Γ will be chosen as the new value for γ.Suppose that there are currently L-1 hidden neurons,SCN will choose the most suitable neuron from many(?Tmax)candidates to be the L th hidden neuron.The output of one neuron can be expressed as

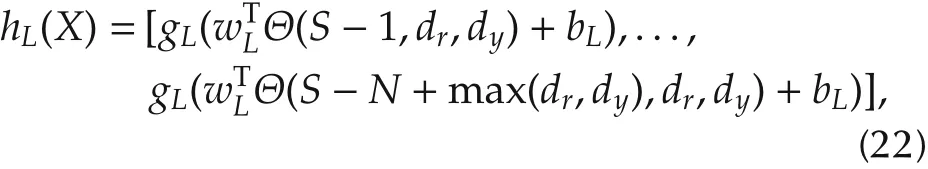
where wL,bLand gLare the weights,biases and activation function of the neuron,respectively.Denoted the current residual error by EL-1(X),and the condition which determines whether the neuron will be the candidates of the L th hidden neuron is

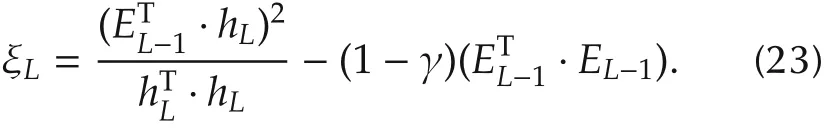
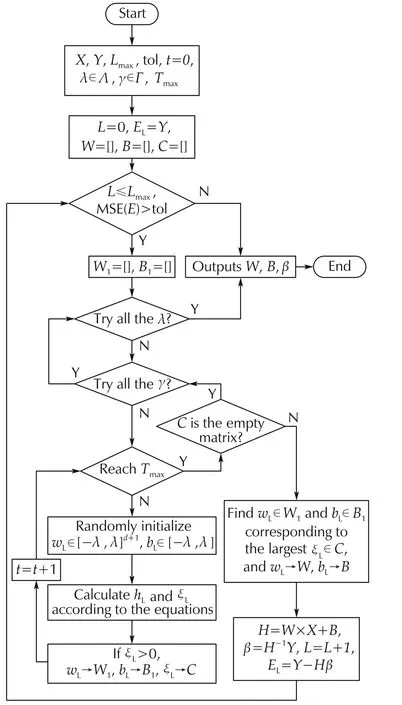
Fig.4 The training process of the stochastic configuration network.

If ξL＞ 0,the neuron will be candidates,and wL,bLand ξLare restored in W1,B1and C,respectively.The candidate with the largest ξLwill finally be the L th hidden neuron.The stopping criterion is that either the upper limit of the number of hidden neurons Lmaxis reached or the root mean square error is smaller than the predifined parameter Tol.According to the weight and the bias matrixes of the hidden layer and the weights of the output layer,the prediction for the high-order nonlinear term can be formulated as

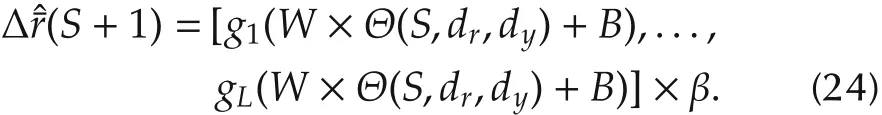
?Alternating identification

The alternating identification of the nonlinear term and parameters is adopted for the accurate ECT prediction[18].After Δr(S+1)is calculated(equation(24)),the parameters F=[F1,...,F11]Tcan be estimated again by the least squre method based on equation(14),

where 0?i?N-2-max(dr,dy).After the new values ofF is calculated,the new tutor signal for SCN can be obtained according to equations(11)and(13).As a result,SCN will be trained further and more accurate estimation of the nonlinear term will be got.Overall,the steps of the alternating identification for ECT prediction model are as follows:

1)Intialize SCN and calculate the initial estimationsbased on the empirical values of the parameters[12]and Table 2.

3)Train SCN and calculate the new estimations ΔR according to equation(24).

4)Calculate the ECT prediction(equation(12))based onin step 2)andin step 3).If the root mean square error of the ECT predictions is smaller than Tol,then stop,otherwise go on to the next step.

5)Calculate the new values ofF based onin step 3)according to equation(25),then go to step 2).

Overall,the ECT prediction model is given in equation(12),where the estimations of the parameters and the high-order nonlinear term are given in equation(25)and equation(24),respectively.

6 Simulation experiments

The data collected from a factory in Liaoning Province(China)are taken for example.The fused magnesium furnace has a designed production capacity of 30 ton.After preprocessing and eliminating outliers,382 sets of oberservations have been finally utilized.The training set is of size 300 while the test set is of size 82.

The current of one electrode in one production batch is plotted in Fig.5.As the current fluctuates dramatically,equation(4)is used to calculate the average current in the smelting process,and yminand ymaxare set to 12000 A and 17000 A,respectively.The parameters in Table 1 are estimated by the experience as in[12]:U can be detected and it is about 190 V;cosφ=0.8 which is estimated by the power consumption,the average current and U;rtheory=1577 kWh/ton is estimated by the energy absorbed by the fusion of MgO and the latent heat of fusion[5];p=0.7 which is estimated by the collected data,that is dividing the product of the actual yield and rtheoryby the actual energy consumption;The values for A,B and C are respectively 34 V,1000 V/m and 0.35 m·kA[19];f1=0.005Ωm,f2=0.001Ωm,and kp=0.2305(kW·mΩ-β·m-1)[20].The initial estimations of F1∼F11can be obtained based on these empirical values of the parameters according to Table 2.

The threshold δ=0.5 when the order of the nonlinear term is identified.Table 3 is the distance correlation of the random variables ΔRi=[Δr(S),Δr(S-1),...,Δr(S-N+1+i)]Tand Ri=[r(S-i),r(S-1-i),...,r(S-N+1)]T,while Table 4 is the distance correlation of the random variables ΔRiand Yi=[y(S-i),y(S-1-i),...,y(S-N+1)]T.As a result,dr=8,dy=4 and the inputs of SCN are Θ(S,dr,dy)=[r(S),...,r(S-7),y(S),...,y(S-3)](equation(19)).

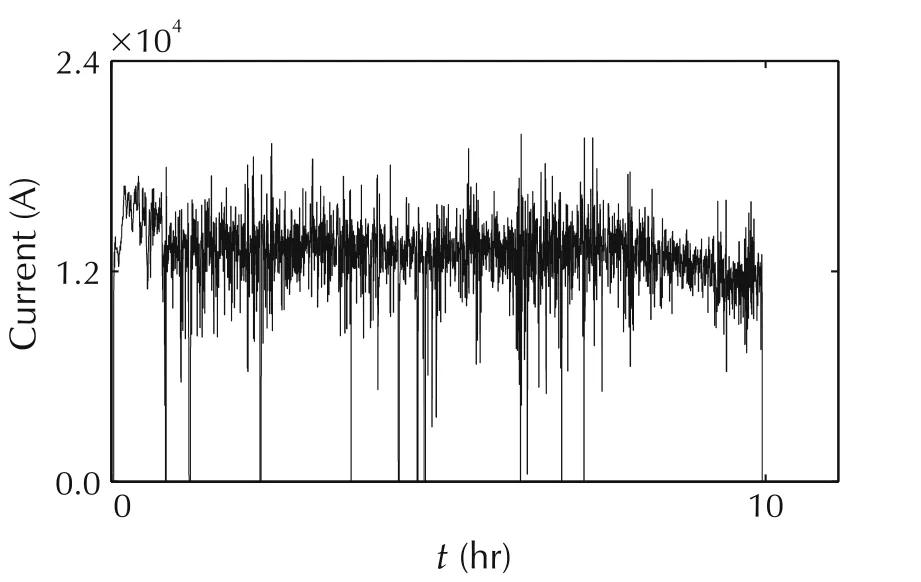
Fig.5 The sampled current of the fused magnesium furnace.

Table 3 The distance correlation of the nonlinear term and the historical ECT values.

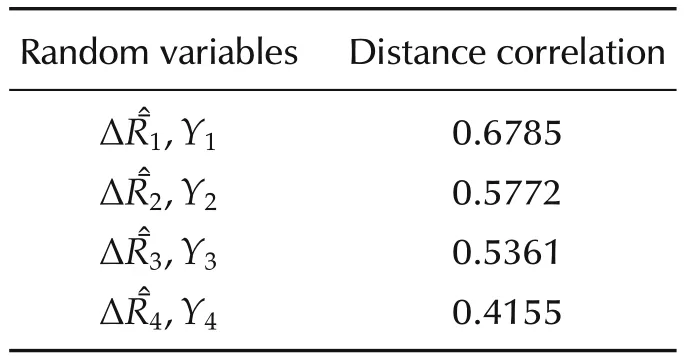
Table 4 The distance correlation of the nonlinear term and the historical average currents.

The settings of SCN is shown in Table 5,and Tol is set to 15 for the stopping criterion in the alternating identification.The root mean square error(RMSE)and the mean absolute percent error(MAPE)are adopted as the performance indicators,

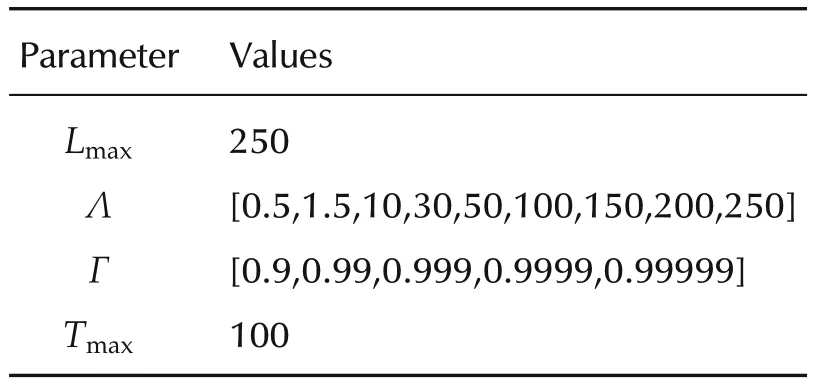
Table 5 The settings of the stochastic configuration network.

Fig.6 shows the change of the parameters in the process of alternating identification.The predicted ECT values by our method and the method of[12]are plotted in Fig.7 and Fig.8,respectively.RMSE and MAPE for the two prediction methods are shown in Table 6.It can be seen clearly that our prediction method can improve the prediction accracy significantly.The histogram of the error distribution and the probability density function of the error are shown in Fig.9,which demonstrates that the prediction results are satisfactory.

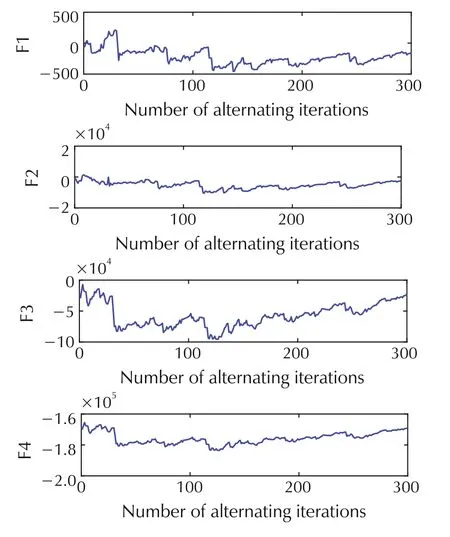
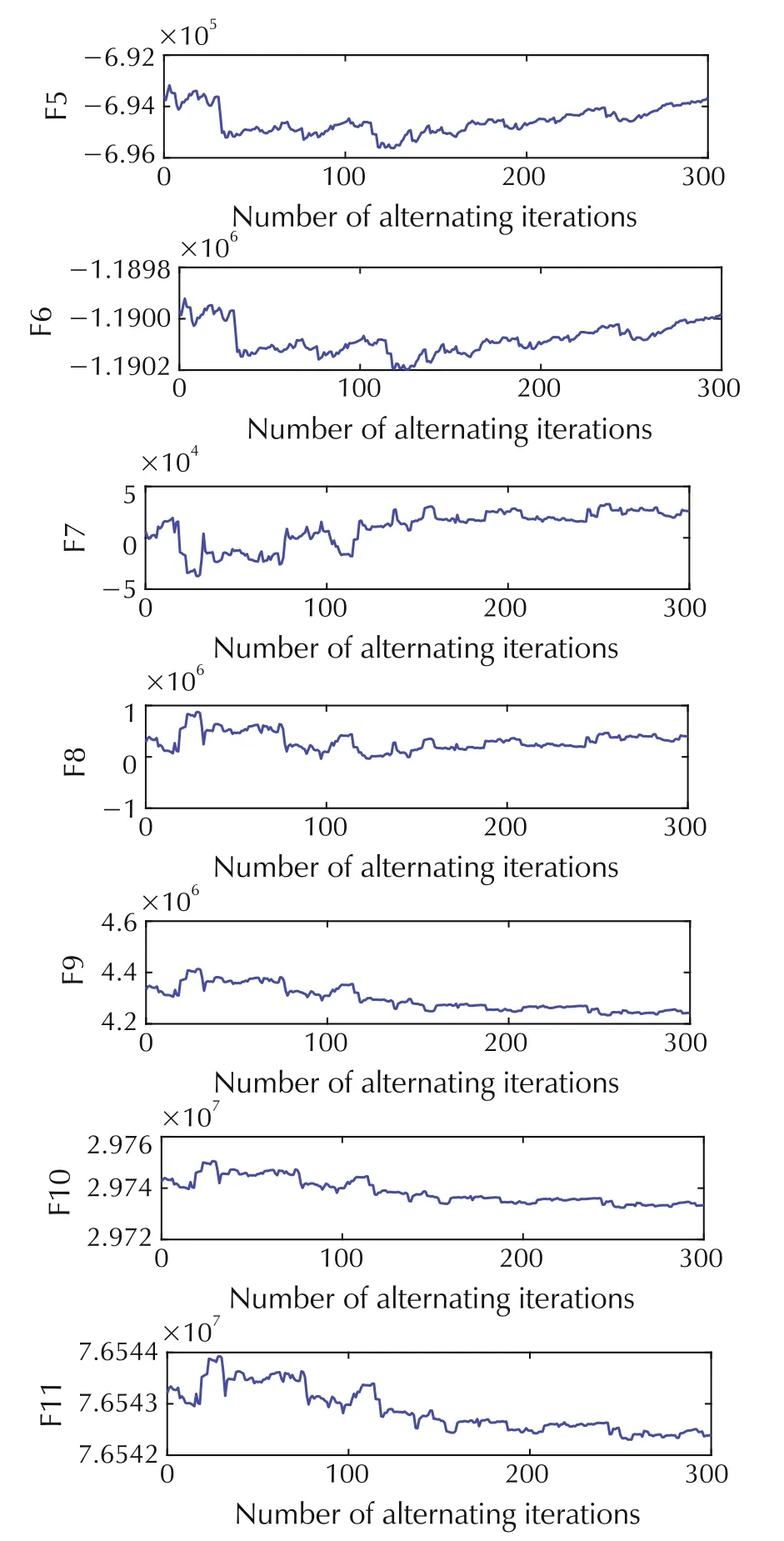
Fig.6 The change of the parameters in the process of alternating identification.

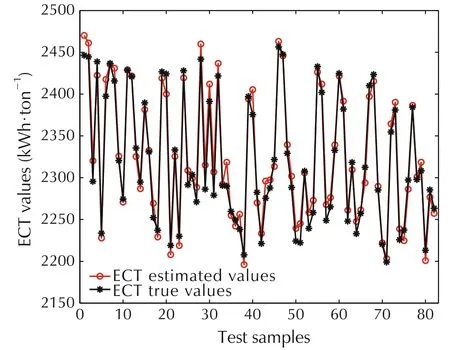
Fig.7 The predicted ECT values by our method.

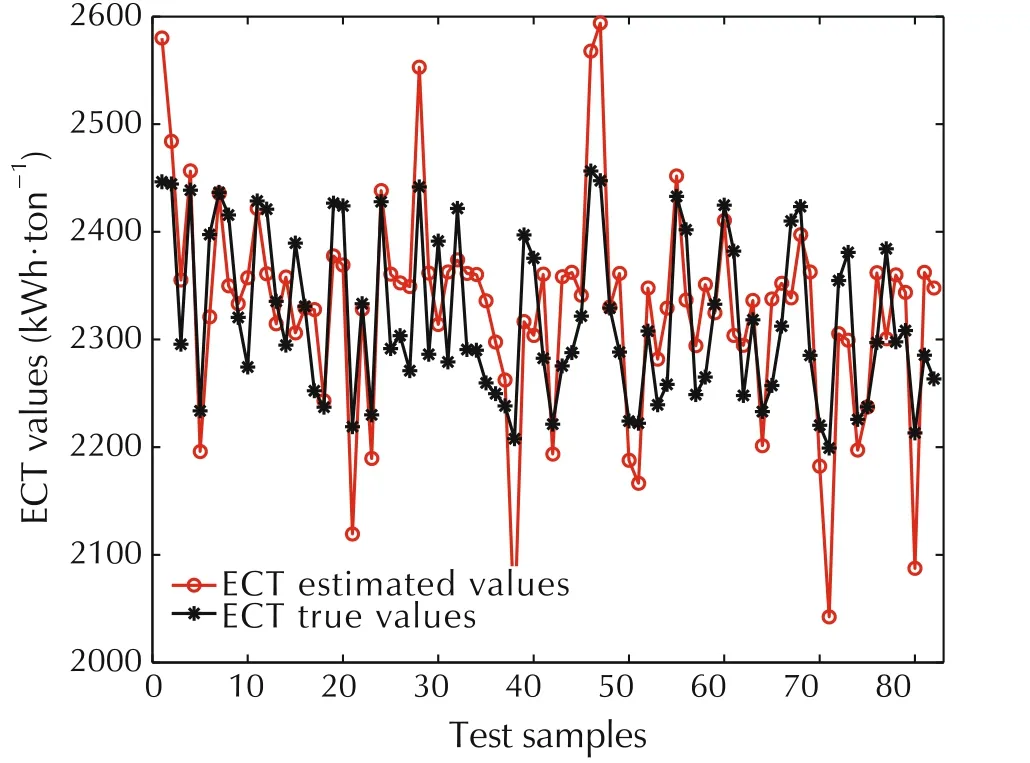
Fig.8 The predicted ECT values by[12].

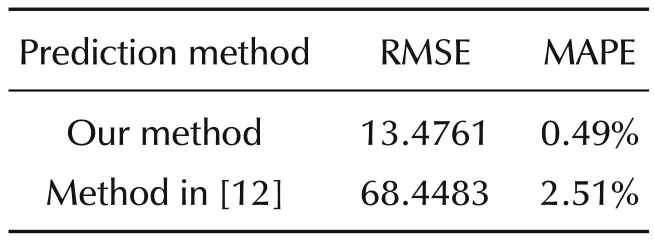
Table 6 RMSE and MAPE for two prediction methods.

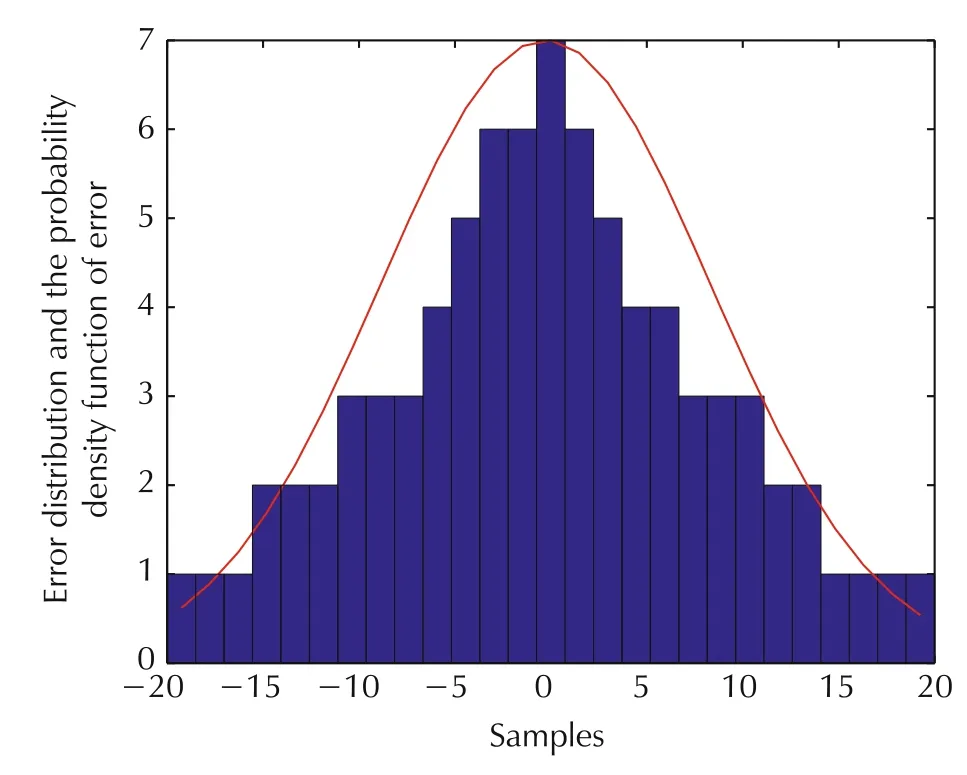
Fig.9 The histogram of the error distribution and the probability density function of the error.

7 Conclusions

This paper builds a dynamic ECT prediction model for different production batches,which is made up of a nonlinear model with unknown parameters and an unknown high-order nonlinear term.The nonlinear model is transformed for the identification of the parameters.A prediction method for ECT is proposed,which includes the order identification of the nonlinear term,the alternating identification ofthe modeland the ECT prediction model.Experiment results based on the real data show that the proposed method can provide accurate ECT predictions,which lay the foundation for the optimal operation for the fused magnesium furnace.