Precedence-constrained path planning of messenger UAV for air-ground coordination

Yulong DING ,Bin XIN ,3†,Jie CHEN ,3

1.School of Automation,Beijing Institute of Technology,Beijing 100081,China;

2.Key Laboratory of Intelligent Control and Decision of Complex Systems,Beijing Institute of Technology,Beijing 100081,China;

3.Beijing Advanced Innovation Center for Intelligent Robots and Systems,Beijing Institute of Technology,Beijing 100081,China

Received 22 July 2018;revised 27 October 2018;accepted 28 October 2018

Abstract This paper addresses an unmanned aerial vehicle(UAV)path planning problem for a team of cooperating heterogeneous vehicles composed of one UAV and multiple unmanned ground vehicles(UGVs).The UGVs are used as mobile actuators and scattered in a large area.To achieve multi-UGV communication and collaboration,the UAV serves as a messenger to fly over all task points to collect the task information and then flies all UGVs to transmit the information about tasks and UGVs.The path planning of messenger UAV is formulated as a precedence-constrained dynamic Dubins traveling salesman problem with neighborhood(PDDTSPN).The goal of this problem is to find the shortest route enabling the UAV to fly over all task points and deliver information to all requested UGVs.When solving this path planning problem,a decoupling strategy is proposed to sequentially and rapidly determine the access sequence in which the UAV visits task points and UGVs as wellas the access location of UAV in the communication neighborhood of each task point and each UGV.The effectiveness of the proposed approach is corroborated through computational experiments on randomly generated instances.The computational results on both small and large instances demonstrate that the proposed approach can generate high-quality solutions in a reasonable time as compared with two other heuristic algorithms.

Keywords:Air-ground coordination,curvature-constrained path planning,precedence constraints,Dubins traveling salesman problem

1 Nomenclature

(xA,yA):UAV position coordinate(unit:m);

hA:UAV heading angle(unit:rad);

vA:UAV flight speed(unit:m/s);

NG:The number of UGVs;

NT:The number of task points;

2 Introduction

Heterogeneous cooperation between unmanned aerial vehicles(UAVs)and unmanned ground vehicles(UGVs)has received considerable attention lately.There are strong complementarities between UAVs and UGVs promising a bright prospect in sensing,communication,payload abilities,and so on[1].An increasing variety of applications in the field ofmilitary[2,3]and civilian[4,5]have shown that by incorporating different types of unmanned vehicles in a mission,accomplishment of more complex tasks with higher precision will be possible.Chen et al.[6]reviewed a number of influential and successful types of unmanned aerial and ground vehicle systems(UAGVSs)and proposed a taxonomy for classification of existing UAGVSs in which different types of UAGVSs can be described in a unified way.

In UAGVSs,multiple UGVs can act as mobile actuators to collaboratively perform dynamic tasks whose states dynamically change(e.g.,see[7,8]).When UGVs are required to accomplish such tasks within a large area,they may be scattered and not be able to get the information about the others and tasks due to their limited perception or environment factors.The isolation may impede their collaborations.In this case,UAVs can serve as messengers for all UGVs to support their indirect communications and report the information about task states and other UGVs,which leads to a novel and interesting type of UAGVS.

By virtue of quick speed and less space constraint[9,10],UAV can fast capture the task and UGV information,and transmit the gathered information to UGVs.UAV needs to fly the task points firstly to collect all task information.After collecting task information,the messenger UAV needs to fly over the effective communication range of UGVs to collect and transmit the information to UGVs,and can achieve the communications relay among the UGVs.The UGVs can update their decisions according to the newestinformation received from the UAV to improve their task efficiency.Therefore,this messenger mechanism can broaden the operating range of UGVs effectively to achieve multi-UGV collaboration in large area.An example of this scenario is shown in Fig.1.

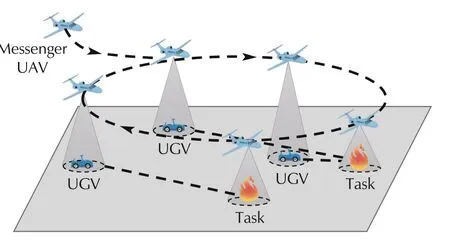
Fig.1 An example of task scenario for a UAGVS operating in large areas.

In this paper,we will focus on the path planning for the messenger UAV in the novel UAGVS mentioned above.It is a new challenging problem which is crucial in achieving the effective air-ground coordination in the UAGVS.

The problem can be regarded as a complex special case of the Dubins traveling salesman problem with neighborhood(DTSPN)described in[11,12],hereinafter also being referred to as the Precedence-constrained dynamic Dubins traveling salesman problem with neighborhood(PDDTSPN).This confronts us with the following challenges:

i)To adapt the UGV’s motion,the UAV path needs to be dynamically computed and updated online by the developed algorithm.This requires the developed algorithm has relatively low computational time.

ii)To plan a flyable UAV tour,we need to generate a smooth trajectory and guarantee that the trajectory respects the kinematic properties of the air vehicle.

iii)This path planning is a complex optimization problem involving mixed variables.Some decision variables are constrained to be integers(e.g.,the sequence of all UGVs for UAV to visit),while other decision variables(e.g.,the access location and the heading of UAV)are continuous variables.

iv)The access sequence for the UAV involves precedence relation:UAV needs to visit all task points firstly and then visit all UGVs.

This paper proposes a novel path planning problem(PDDTSPN)which arises in a novel UAGVS with messenger mechanism.To our best knowledge,this online path planning problem is discussed for the first time.In addition,when solving this path planning problem,we apply a decoupling strategy to decompose the problem into two subproblems:one is to determine the sequence of task points and UGVs for the UAV to visit,and the other is to optimize the access locations of UAV in the neighborhood of each task point or each UGV.This strategy can achieve a desirable tradeoff between solution quality and time cost.

This work contrasts with our previous work[13]that focuses on path planning of messenger UAV which just needs to visit all UGVs and does not consider visiting task points.Our previous work assumes that all task states are static and known by UGVs in advance.However,in practice,the task states may change,and UGVs need to dynamically adjust their plans according to the state of each task.The UAV needs to collect the task information and then inform all UGVs.Therefore,compared with ourprevious work,this work is more suitable for air-ground coordination in dynamic tasks.

The paper is organized as follows.Section 3 will give a formal problem definition.Section 4 will present a heuristic method to determine the sequence of task points and UGVs for the UAV to visit.Section 5 will optimize the access locations of UAV in the neighborhood of each task point or each UGV.Section 6 will demonstrate the performance of our algorithm with some simulations.Finally,Section 7 will conclude the paper.

3 Problem formulation

A small fixed-wing UAV is chosen as a messenger.The motion parameters of UGVs(e.g.,velocity and trajectory)are known by the UAV.Given the initial locations of moving UGVs and their motion parameters,the messenger UAV is responsible for flying over each moving UGV to acquire the information about UGVs and transmit the information about the others.In practice,UGVs and UAVs generally have limited communication range.Only when entering the communication range of each other,can they exchange information.In other words,UAV can transmit information to a UGV only if the messenger UAV is located within the communication range of the UGV.We specify the neighborhood of the UGV as a disk centered at the UGV in this paper.The valid communication radius for the UAV and the UGV i(i∈{1,2,3,...,NG})are denoted byandrespectively.In addition,each task point can be regarded as a fixed UGV.The neighborhood of the task point can be defined as the perceivable range of UAV for the task point.The neighborhood radius of the task i(i∈{1,2,3,...,NT})is denoted by

When planning paths,the UAV just needs to pass neighbourhoodsofallUGVs,ratherthan flying overtheir precise locations.Hence,it is demanded that UAV can plan a path to traverse the access location in each UGV’s neighbourhood according to the planned sequence ofall UGVs for the UAV to visit in the shortest time,where assume that information can be instantaneously transmitted from the UAV to each UGV.The planned sequence of all UGVs for the UAV to visit(briefly called the visiting sequence of UGVs)are denoted by SG=where(i∈{1,2,3,...,NG})is the index of the UGV for UAV to visit.For instance,SG=(3,1,2)means that UAV needsto visitUGV3,UGV1 and UGV2 in sequence.The access location,the access heading and the access time to visit the neighborhood of the UGV i(i∈{1,2,3,...,NG})are denoted by Pi,hiand ti,respectively.

In the same way for all task points,the UAV also just needs to access neighbourhoods of task points according to the planned visiting sequence.Let ST=be the visiting sequence of task points where sGi(i∈{1,2,3,...,NT})is the index of the task point for UAV to visit.Since task point can be regarded as a fixed UGV,the access location,the access heading and the access time to visit the neighborhood of the task point i(i∈{1,2,3,...,NT})can be represented by Pi,hiand tirespectively.

In order to acquire a smooth and feasible path for messenger UAV,the Dubins model is used to describe the kinematic characteristics of the UAV.The Dubins model[14]is used to describe the aerodynamic of vehicles on a two-dimensional plane,and satisfies the following curvature motion constraints:

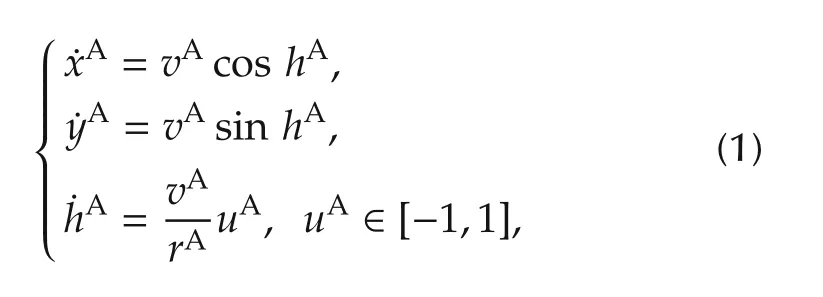
where rAis the minimum turning radius of the Dubins vehicle,uAis the control input,and(xA,yA,hA)represents the status of the Dubins vehicle(UAV),also called Dubins status.The definitions of vA,xA,yAand hAare given at the beginning of this paper.

It is known that there are six possible shortest path patterns,called Dubins paths,between any two configurations:RSL,LSR,RSR,LSL,RLR,and LRL[15],where L means turning left with the minimal turning radius,R means turning right with the minimal turning radius,and S means moving along a straight line.The shortest Dubins path between two configurations relies on both their positions and their.We use the optimal Dubins path under terminal heading relaxation[16,17]to describe the paths of the messenger UAV.For Dubins paths with terminal heading relaxation,once the initial heading of UAV is fixed,the heading at the terminal point is determined by their relative position.The length of the shortest path of a Dubins vehicle from Dubins status(xA,yA,hA)to a point PB∈R2with terminal heading relaxation is denoted as D((PA,hA),PB)where PA=(xA,yA).In the sense of terminal heading relaxation,the number of variables of Dubins paths can be decreased,which can effectively reduce the computational complexity[11].

Forthe messenger UAV,the travelcostbetween every pair of task points and UGVs can be measured by the length of the Dubins path between them.The objective of the problem J is to determine a path with minimum cost for the messenger UAV when the UAV traverses the valid neighbourhood of each task point and each UGV.We model the messenger UAV’s path planning as a PDDTSPN in which UGV’s locations dynamically change.The PDDTSPN model in the sense of terminal heading relaxation is represented as follows:

Constraint(4)ensures that the messenger UAV is located within the communication range of each UGV while Constraint(5)ensures that the messenger UAV is located within the communication range of each task point.Constraint(6)states the precedence constrainton visiting task points and UGVs.

To get a solution to the PDDTSPN,the visiting sequence of task points and UGVs(S＊)and the access locations for each neighborhood of task points and UGVs(P＊)should be determined.By relaxing dependencies between S＊and P＊,we develop an online algorithm to determine the visiting sequence at first,and then optimize the rendezvous path in each UGV’s neighborhood.

4 Heuristic for determining the visiting sequence

Generating the optimal visiting sequence through the neighborhoods of the task points and the UGVs is NP-hard.However,the complexity issue is an importantpart of an online algorithm,since the UAV path needs to be dynamically computed and updated,and therefore determining the visiting sequence should not become prohibitively time-consuming.An efficient approximation algorithm is used to determine the visiting sequence.The main idea of the approximation algorithm is that the optimal precedence-constrained Euclidean traveling salesman problem(PETSP)tour is computed for all task points as well as all UGVs,and then the order of visits for the PETSP is used as the visiting sequence for the UAV.

Considera complete undirected graph G=(V,E)with a set of vertices V representing the task points and the UGVs to be visited,and a set of arcs E={(vi,vj):i≠j,vi,vj∈V}connecting these vertices.The vertex set V can be partitioned into two clusters:one cluster is the set of task points VT={v1,...,vNT}and another is the set of UGVs VG={v1,...,vNG}.E is associated with a cost matrix C=[cij](NT+NG)×(NT+NG)representing the Euclidean distances between vertices viand vj(vi,vj∈V).The goal is to determine the shortest tour on G in which all vertices in V are visited only once,and VTare visited before VGare visited.

Lokin et al.[18]transformed this problem into a stan-dard traveling salesman problem(TSP)by modification of the cost matrix.The cost matrix is modified by adding a large number M(M ≫ max{cij},∀ij)to the cost of each intercluster edge in matrix C,that is

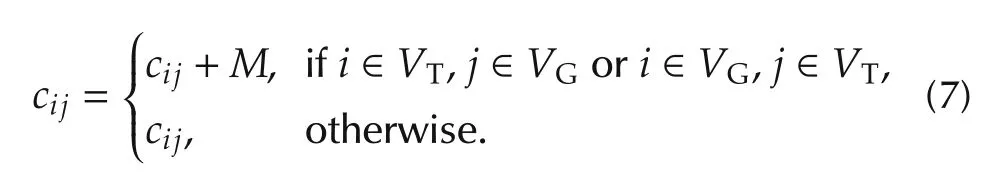
After the transformation,any exact algorithm for TSP can be applied to solve PETSP exactly[19].The Lin-Kernighan heuristic algorithm proposed by Helsgaun etal.[20]is very effective to solve TSP.The visiting sequence will be obtained by means of the Lin-Kernighan heuristic algorithm with respect to the transformed matrix.

To adapt to the change of UGVs’locations,the idea of receding horizon optimization proposed in[21]is used to dynamically modify and update the visiting sequence:

i)Atany time,the UAV needs to determine the visiting sequence by using the above algorithm,taking into account the current position information of all task points and UGVs.

ii)Apply the resulting visiting sequence to compute the path of the UAV to visit the next task point or UGV.

iii)Repeat i)and ii)until all task points and all UGVs are visited.

5 Optimization of access location

In this section,we will optimize the access location in the neighborhood of each UGV and each task point.

5.1 UAV paths to visit a moving point

Lemma 1(Theorem 1 in[13])Assume that the UAV can obtain a point trajectory p(t)=(xp(t),yp(t))in advance,and the maximum speed ofthe movingis less than the UAV speed＜ vA).There exists t＊(t＊∈ [tmin,tmax]),such that

Assume that the UAV can obtain the trajectory of p(t)in advance and＜vA.According to Lemma 1,the UAV can visit a moving point at the time interval[tmin,tmax].Accordingly,in order to obtain the UAV path to visit a moving UGV,we need to determine the time interval[tmin,tmax]at first,and then obtain an approximative numerical solution for t＊by a bisection approach.Furthermore,the UAV path to visita moving UGVand its corresponding rendezvous point Pr(t＊)can be obtained.The detailed steps are shown in Algorithm 1.

Algorithm 1(UAV path planning to visit a moving UGV)Initialization:Given the point trajectory p(t)=(x p(t),y p(t)),the initial solution interval[t min,t max]from(8)and(9),define T(t)=D((P A initial,h initial),p(t))/v A-t.Repeat Find the midpoint t c=(t min+t max)/2 and then compute T(t min)and T(t c).Update the solution interval[t min,t max].If T(t min)·T(t c)＞ 0 then t min=t c,else t max=t c.End if Until The desired accuracy is reached.t＊=(t min+t max)/2.The path to visit a moving UGV is a Dubins path from P A initial to the rendezvous point P r(t＊).

Apparently,the accuracy of the solution depends on the number of iterations,and can reach(tmax-tmin)/2Nbafter Nbiterations.

5.2 Determining access location in each neighborhood

Considering the limited communication range of UGV,a messenger UAV will achieve communication with UGVs as long as the UAV visits the UGV’s neighborhood.Itis clearthatUAVmustgo through the boundary if it wants to visit any point in a neighbourhood,so we only consider the boundary points in the UGV’s effective and reliable communication range.If the motion trajectory of the UGV is P(t)=(xG(t),yG(t)),the point on the boundary of the UGV’s communication range can be represented precisely by its polar coordinates with respect to the centre of the neighbourhood.The trajectory of the boundary point can be described as P(β,t)=(xG(t)+cos β,yG(t)+sin β),where β is the central angle from x-axis.Obviously,different β may lead to different rendezvous points with UAV.

As shown in Fig.2,when β =2π/3,the rendezvous point of the UAV and the boundary of the UGV’s communication range is A′and the location of the UGV is A at the moment;when β =0,the rendezvous point is B′and the location of the UGV is B at the moment.Therefore,the problem of finding the access location of the UAV can be transformed into an equivalent problem of finding the optimal rendezvous point on the boundary of the UGV’s communication range.

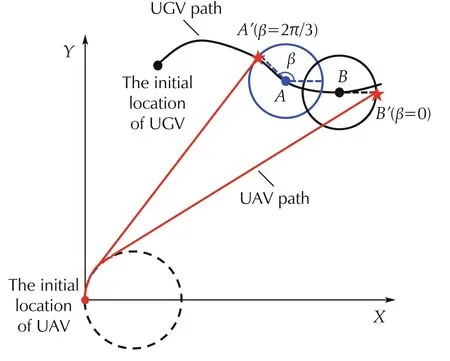
Fig.2 Different rendezvous points when considering the UGV’s communication range.

A sampling-based approximation method is proposed to optimize the access location in each UGV’s neighborhood.Uniform sampling on the boundary of the UGV’s neighborhood is implemented(the sampling number is Nsample).For any sampling point m(m=1,2,...,Nsample),the rendezvous pointand its corresponding headingcan be obtained by Algorithm 1.To obtain solutions with higher quality,the path fromto the next UGV is taken into consideration.According to)and,Algorithm 1 is used again to obtain the rendezvous pointfor the next UGV and its corresponding rendezvous time t＊＊.Furthermore,calculate the Dubins distance

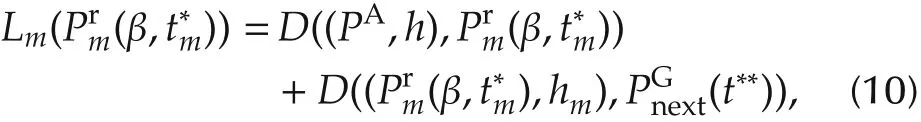
where PAand h are the current location and the heading of the UAV,respectively and hmis the heading of the UAV at

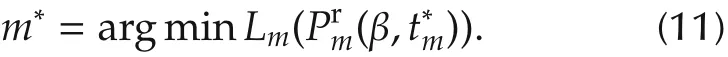
m＊is easy to be obtained by enumeration forallsampling point m(m∈{1,2,...,Nsample}).The access location of the UAV is

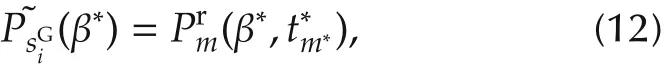
In the same way,the access location in the neighborhood of each task point can be determined.

5.3 Planning multiple Dubins loops

To collect and transmit the information,the UAV needs to fly over all task points and all UGVs periodically,and consequently,should complete the planning of multiple Dubins loops.In each single Dubins loop,all task points and all UGVs need to be visited only once.Planning multiple Dubins loops resembles the planning of a single Dubins loop many times.The main difference is that the initialization of the visiting sequence needs to be performed before each Dubins loop.The overall process of our approach is shown in Algorithm 2.

Algorithm 2(UAV’s path planning constrained by moving UGVs)Initialization:The initial location of the UAV is P A is the number of the Dubins loops and vector X k=initial.N loop{xk 1,xk 2,...,xk N G+N T}(k=1,2,...,N loop)indicates whether or nottask points and UGVs are accessed atperiod k,i.e.,xk i=0 means that the UGV i has not been visited at the k th period.For k=1:N loop do X k=01×(N G+N T).For n=1:N G+N T do According to X k,determine the set of non-visited UGV Qkn in current period.Utilize the heuristic method proposed in Section 4.1 to determine the visiting sequence S in the set Qkn.Note that si∈S is the next UGV or the next task point that the UAV will visit.Let xksi=1.For m=1:N sample do Given the sampling point m,compute the rendezvous point Pm,and then calculate Lm from(10).End for ObtainPsi(β＊)by(12).P A=Psi(β＊),P G i=P G i(tsi),i=1,2,...,N G.End for End for Update P A and P G i(i=1,2,...,N G).

The computational time of our approach is mainly composed of two parts:the time for determining the visiting sequence and optimizing the access locations.

The time complexity of determining the visiting sequence for each UGV or task point is O(NT+NG).As discussed in Section 4,the process of determining the visiting sequence is based on the receding horizon optimization.Afterthe messengerUAV visitsa UGVora task point,the visiting sequence needs to be re-determined,so the visiting sequence needs to be determined NT+NGtimes.Therefore,the time complexity ofdetermining the visiting sequence is

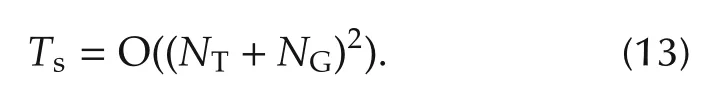
Assume that,when optimizing the access location in a UGV’s neighborhood,the sampling number Nsampleis a constant.According to Section 5.2,the time complexity of optimizing the access locations is

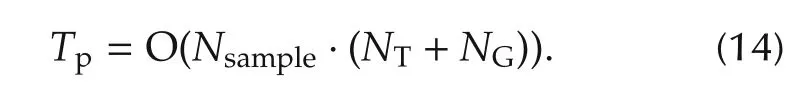
Therefore,the total computational complexity regarding a Dubins loop is

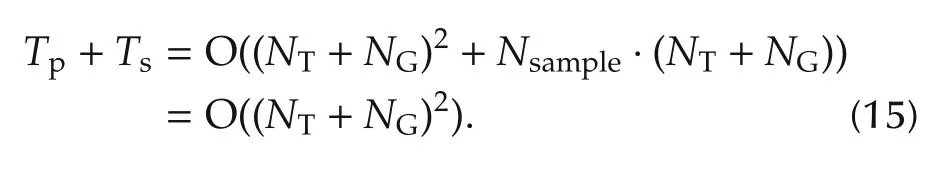
6 Computational experiments

To evaluate the approach proposed in this paper,three computational experiments are conducted in this section.Experiment 1 shows the performance of our method to solve PDDTSPN.Experiment 2 is a comparative experiment in representative scenarios.Experiment3 is a comparative experiment with different problem scales.Allexperimentswere implemented in Matlab environment on a PC with Intel(R)Core(TM)CPU i5-4590 3.3 GHz,and 4 GB RAM.

6.1 Performance analysis

Fig.3 shows a solution of the path planning of the messenger UAV constrained by the motion of UGVs.In this case,there are two task points whose locations are=(35,0)m and=(-10,-30)m,respectively.There are two UGVs whose initial locations are(0)=(-35,30)m and(0)=(10,30)m,respectively.UGV 1 moves towardwith the speed vector(1.83,-0.79)m/s,while UGV 2 moves toward PT2with the speed vector(-0.63,-1.90)m/s.=2.5 m(∀i∈{1,2,3,...,NT}),=2.5 m(∀i ∈ {1,2,3,...,NG})and Nloop=2.

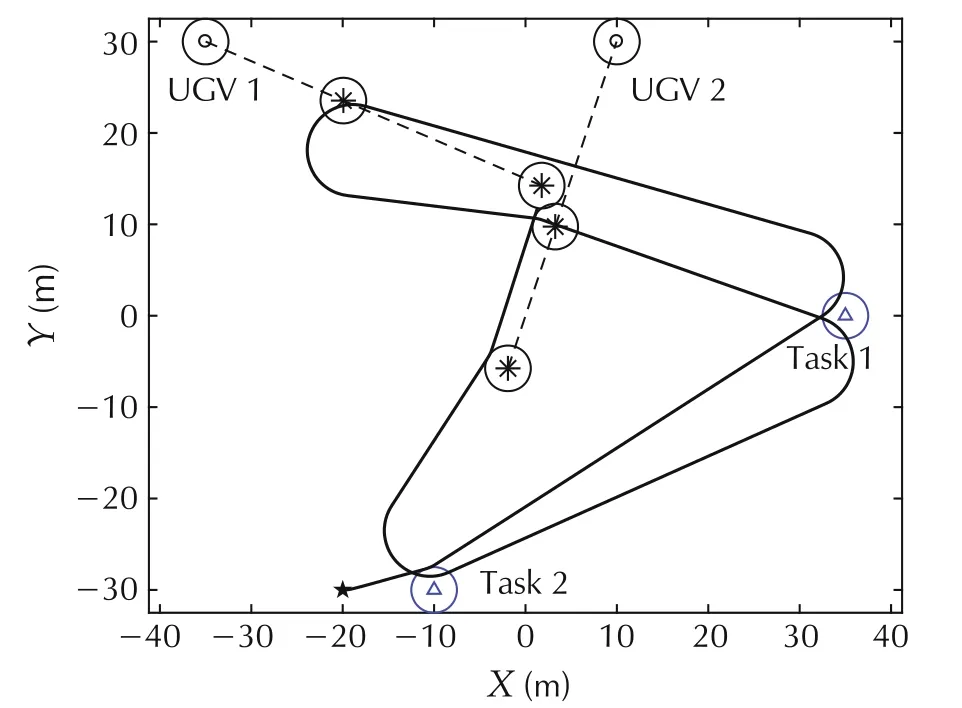
Fig.3 Path planning of the messenger UAV.The scenario consists of two UGVs and two task points.

As shown in Fig.3,according to the location of task points and the motion parameters of the moving UGVs,the messenger UAV can dynamically plan its path to visit the neighborhood of each task point firstly and then visit that of each moving UGV.In addition,the UAV can adjust its visiting sequence to adapt to the changing location of UGVs.In the first loop,the visiting sequence is Task1-Task2-UGV2-UGV1.However,with the movement of UGVs,the visiting sequence becomes Task2-Task1-UGV1-UGV2 in the second loop.

6.2 Comparative experiment in different representative scenarios

To investigate the performance of the algorithm proposed in this paper,we compare the results using the following methods for determining the access location:

1)Boundary sampling(BS,our method proposed in Section 5.3):the access locations corresponding to each task point and each UGV are the boundary points of the communication neighborhood of each task point and each UGV.

2)Center sampling(CS):the access location is the center of the communication neighborhood of each task point and each UGV.

The visiting sequences of the two methods are obtained by using the heuristic method proposed in Section 4.1.

Solutions of the two methods in the three representative scenarios are shown in Figs.4-6.The presented results were obtained with the following parameters:

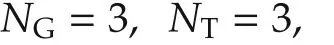
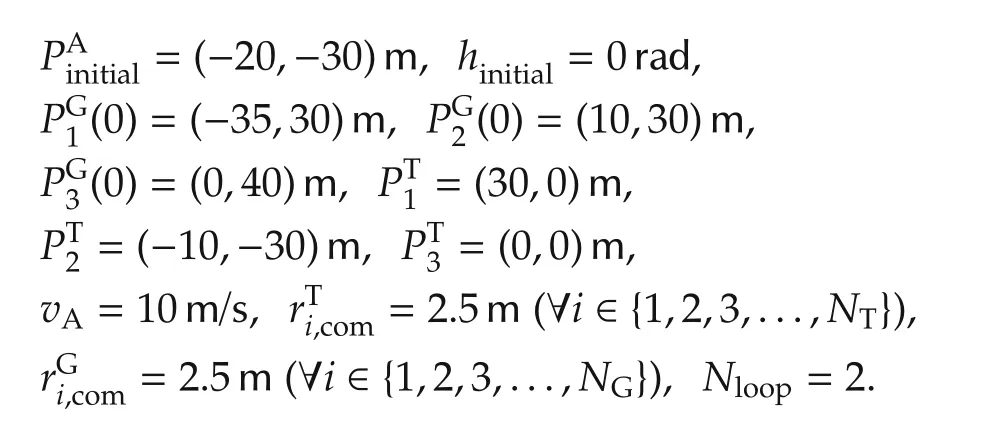
In Scenario 1(see Fig.4),all UGVs are fixed.In Scenario 2(see Fig.5),all UGVs move at different speed vectors.In Scenario 3(see Fig.6),UGV1 has a change of its speed during 5 s＜ t＜ 15 s while the motion parameters of the other UGVs are same with those of the corresponding UGVs in Scenario 2.From the analysis of these solutions in the three scenarios,it can be seen that the paths generated by CS and BS can make the messenger UAV visit/revisit the communication neighbourhood of the moving UGVs periodically.

Table 1 shows the tour lengths and the average computing time for visiting each task point or each UGV used by the above two methods in the three representative scenarios.It can be seen that the lengths of Dubins tours obtained by CS are longer.For CS,the UAV needs to pass the center of each communication neighborhood,which can be regarded as a special case of BS.Compared with CS,sampling on the boundary in BS can provide larger search space,and therefore contribute to finding solutions with higher quality.Table 1 also indicates that CS is much faster than BS.BS has to search the neighbourhood of each task point or each UGV and consumes more time.However,the time cost of BS,approximately 0.2 s,is acceptable.

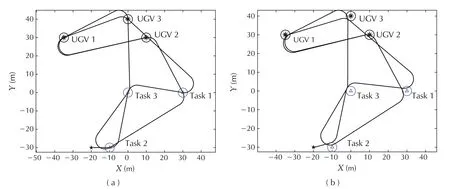
Fig.4 Scenario 1:all UGVs are fixed.(a)Path planned by CS.(b)Path planned by BS.

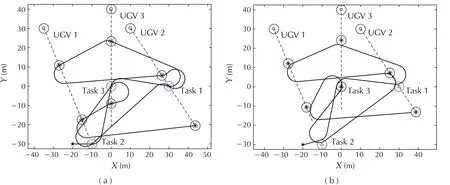
Fig.5 Scenario 2:→v UGV1=(0.6,-1.4)m/s,→v UGV2=(0.8,-1.2)m/s,→v UGV3=(0,-1.5)m/s.(a)Path planned by CS.(b)Path planned by BS.

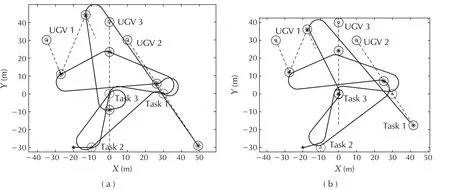
Fig.6 Scenario 3:When t ＜ 5 s,→v UGV1=(0.6,-1.4)m/s;when 5 s＜ t ＜ 15 s, →v UGV1=(0.6,1.4)m/s;when t ＞ 15 s,→v UGV1=(0.6,-1.4)m/s.The speed of the other UGVs are similar to the corresponding UGVs in Scenario 2.(a)Path planned by CS.(b)Path planned by BS.

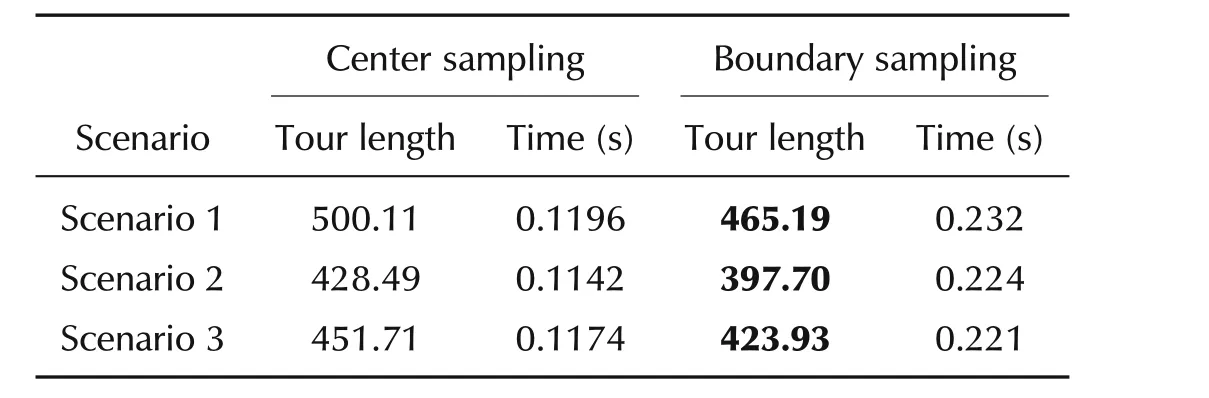
Table 1 Lengths of Dubins tours and time cost corresponding to the scenarios shown in Figs.4-6.

6.3 Comparative experiments on instances with different problem scales

In this section,comparative experiments on different instances are conducted to evaluate the scalability of our approach.The tested instances are labelled as Instance-N-i,where N is the number of task points,and i is the number of UGVs.For example,Instance-6-3 indicates 6 task points and 3 UGVs.In this subsection,all initial locations of UAV,UGVs and task points are generated randomly,the speed vectors of UGVs are also random vectors and Nloop=1.

BS is compared with two algorithms:CS and a modified version of algorithm proposed in[13].In[13],a geometry-center-based(GC)method was used to determine the visiting sequence but did not consider precedence constraints on task points.To access all task points firstly,determine the visiting sequence for task points using the geometry-center-based method at first,and then determine the visiting sequence for all UGVs using the same method.

The results obtained by the three algorithms over a set of 14 benchmark instances are reported in Table 2.As shown in Table 2,the approximate optimal solution J＊is recorded for BS,and the optimal solutions found by CS and GC are recorded and labeled by JCSand JGCin Table 2,respectively.The gap between BS and CS is calculated as GAP1=(JCS-J＊)/JCSwhile the gap between BS and GC is calculated as GAP2=JGC-J＊.GAP1is recorded in percentage.The elapsed time for the computation of each algorithm is also recorded(see Table 2).Note that the elapsed time for the computation is the average computing time for visiting each task point or each UGV.The shortest path lengths for every instance are shown in bold.

As shown in Table 2,BS fully outperforms CS in term of solution quality for different instances(see GAP1in Table 2).GAP1increases markedly with the increase of the problem scale,ranging from 10.10%to 53.77%.The paths generated by GC are shorter than those of CS and BS on small instances(e.g.,instance-4-4 and instance-10-15).However,on the larger instances,the paths found by GC are much longerthan those ofCS and BS(e.g.,instance-100-100 and instance 60-150).This is because the greedy nature of GC makes it difficult to accommodate the complex spatial relationships among UGVs and task points with the increase of the problem scale.

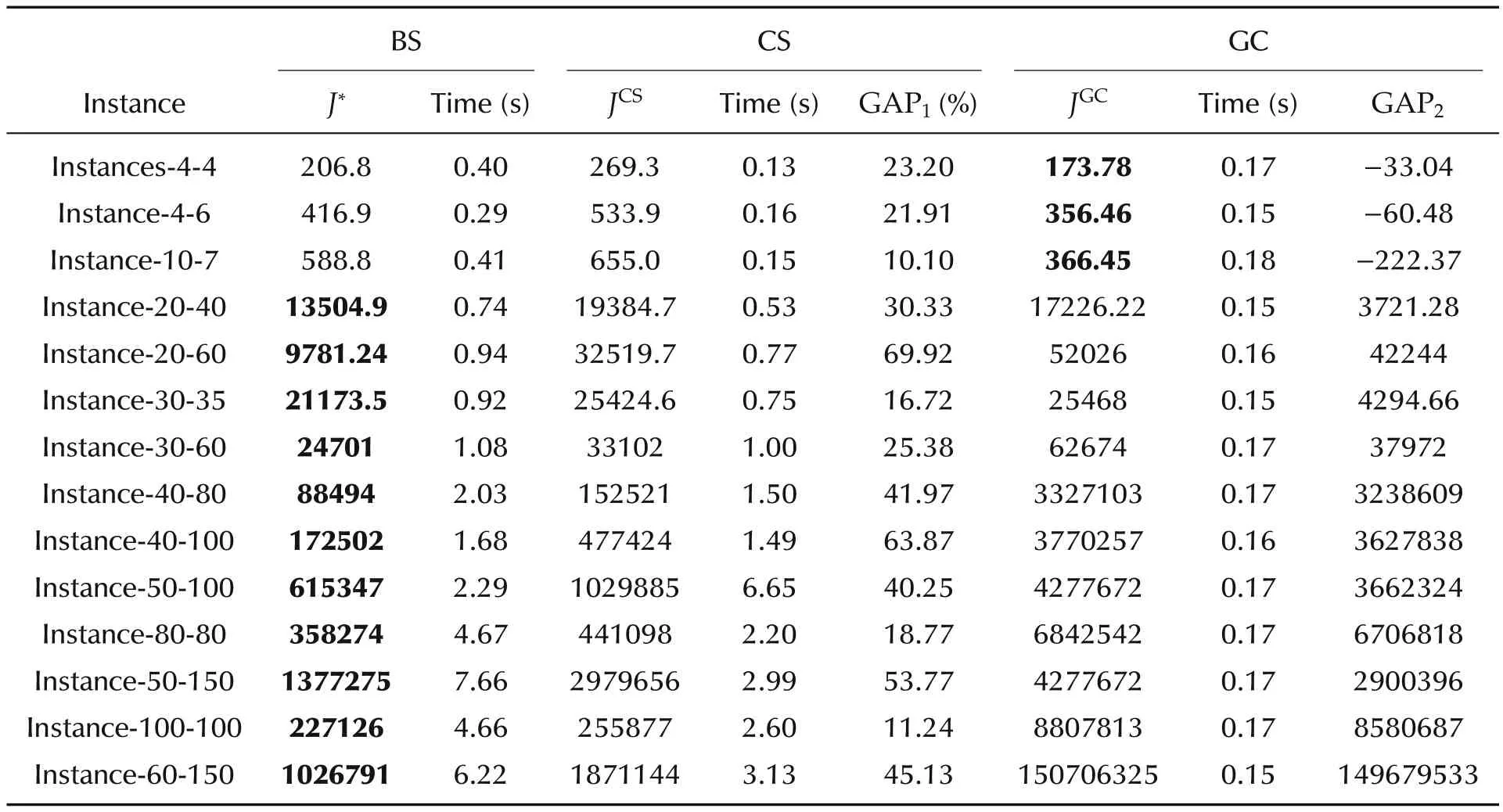
Table 2 Computational results of CS,GC and BS on 14 instances.

7 Conclusions

We present a novel path planning problem that arises in dynamic coordination between UGV and messenger UAV in air-ground coordination.This problem can be formulated as a PDDTSPN.We propose an algorithm in which a decoupling strategy is used to decompose the problem into two subproblems:one is to determine the visiting sequence of all tasks and UGVs and the other is to optimize the access locations of UAV in the neighborhood of each UGV.In our algorithm,a fast heuristic method was used to produce the precedenceconstrained visiting sequence,while a boundary-based sampling method was adopted to optimize the access location of UAV in the neighborhood of each task point and each UGV.

Experiments in representative scenarios demonstrate that the paths generated by our algorithm can make the messenger UAV reliably and rapidly fly over the effective range of the task points and UGVs to collect and transmit the information.The computational results on both small and large instances demonstrate that the proposed approach can generate high-quality solutions in a reasonable time in contrast to two other algorithms.In the future work,the proposed approach willbe extended to consider that the messenger UAV has incomplete or no information about the motion of UGVs in advance.