A new semi-tensor product of matrices

Daizhan CHENG ,Zequn LIU

1.The Key Laboratory of Systems and Control,Academy of Mathematics and Systems Sciences,Chinese Academy of Sciences,Beijing 100190,China;

2.University of Chinese Academy of Sciences,Beijing 100049,China

Received 7 August 2018;revised 10 October 2018;accepted 12 October 2018

Abstract A new matrix product,called the second semi-tensor product(STP-II)of matrices is proposed.It is similar to the classical semi-tensor product(STP-I).First,its fundamental properties are presented.Then,the equivalence relation caused by STP-II is obtained.Using this equivalence,a quotient space is also obtained.Finally,the vector space structure,the metric and the metric topology,the projection and subspaces,etc.of the quotient space are investigated in detail.

Keywords:Second sime-tensor product(STP-II),equivalence class,quotient space,topology,metric

1 Introduction

As a generalization of conventional matrix product,the semi-tensor product(STP-I)is defined as follows:

Definition 1 Let A ∈ Mm×n,B ∈ Mp×q,and t=n∨p be the least common multiple of n and p.Then the left semi-tensorproduct(STP-I)of A and B,denoted by AB,is defined as

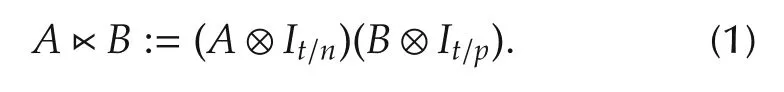
The rightSTP-Iof A and B,denoted by AB,isdefined as

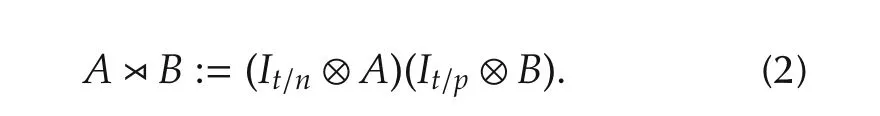
We use▷◁for eitheror.Since has better properties than,STP-I is defaulted to be left STP-I next unless elsewhere stated.

When n=p STP-I becomes the conventional matrix product.Hence it is a generalization of conventional matrix product.Though the conventional matrix product has been extended to STP-I,which is applicable to two arbitrary matrices,its all properties remain available.

STP-I was firstly proposed in 2001[1].Since then it has received many applications,and becomes an important tool in stabilization and control design of dynamic systems,e.g.,power systems[2];analysis and control of logical systems[3];finite games[4,5];etc.

In recent study on cross-dimensional linear systems[6],a projection Pr:Mm×m→ Mkm×kmis proposed as

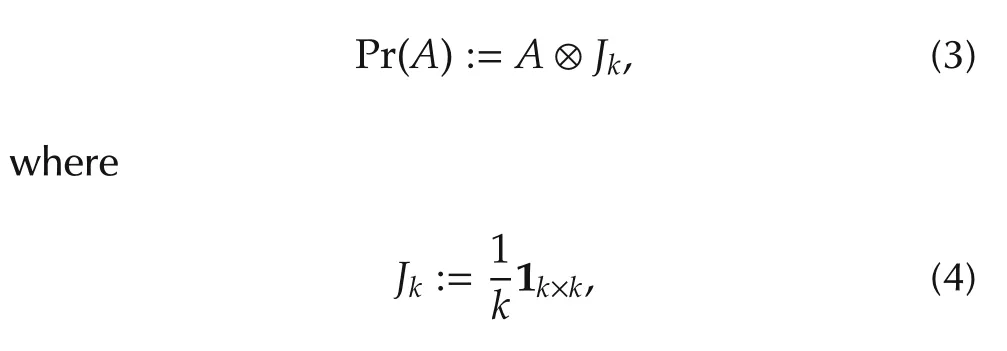
that is,Jkis a k×k matrix with 1/k as its all entries.This fact motivates us to define the STP-II as follows.

Definition 2 Let A ∈ Mm×n,B ∈ Mp×q,and t=n∨p be the least common multiple of n and p.Then the second left(right)semi-tensor product(STP-II)of A and B,denoted by A °ιB(correspondingly,A °rB),is defined as

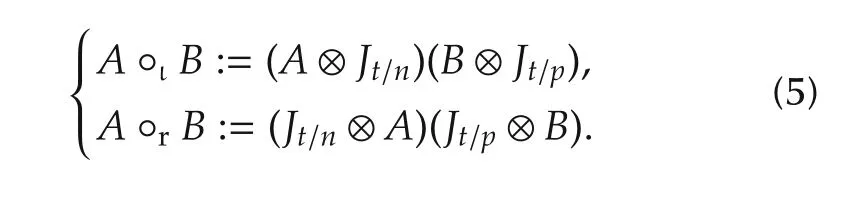
We use°for both left and right STP-II.It is obvious that°is also a generalization of conventional matrix product.

We may also call STP-I and STP-II by first matrixmatrix(MM-1)product and second matrix-matrix(MM-2)product,because both of them are matrix-matrix product.The purpose of this paper is to introduce the concept of STP-II,and then to investigate the properties of STP-II.Some related topics are also discussed,which include 1)equivalence and quotient space;2)lattice structure ofequivalence class;3)vectorspace structuresofmatricesand theirequivalence classes;4)matric space structure and its matric topology;and 5)projection and subspaces.Most of the results are presented without proofs,because they have their corresponding known results for first STP.Then the original proofs can easily be revised to provide proofs for corresponding results of STP-II.

It seems to us that STP-II is also a very useful tool in investigating cross dimensional dynamic(control)systems[6].

The rest of this paper is organized as follows:Section 2 provides some fundamental properties of STPII.Section 3 proposes an equivalence called the STP-II equivalence.Based on the STP-II equivalence,a quotient space is obtained in Section 4.Section 5 proposes a vector space structure on quotient space.Sections 6 and 7 consider the metrics on matrix space and its quotient space respectively.The metric topology is also presented.Section 8 investigates the subspaces of quotient space.Section 9 is a brief conclusion.

2 Some fundamental properties

Thissection considerssome basic propertiesofSTP-II.Most of them have their corresponding ones for STP-I.

First,we consider Jk.Some of its properties,mentioned in the follows,are easily verifiable.Hence,the proofs are omitted.

Proposition 1

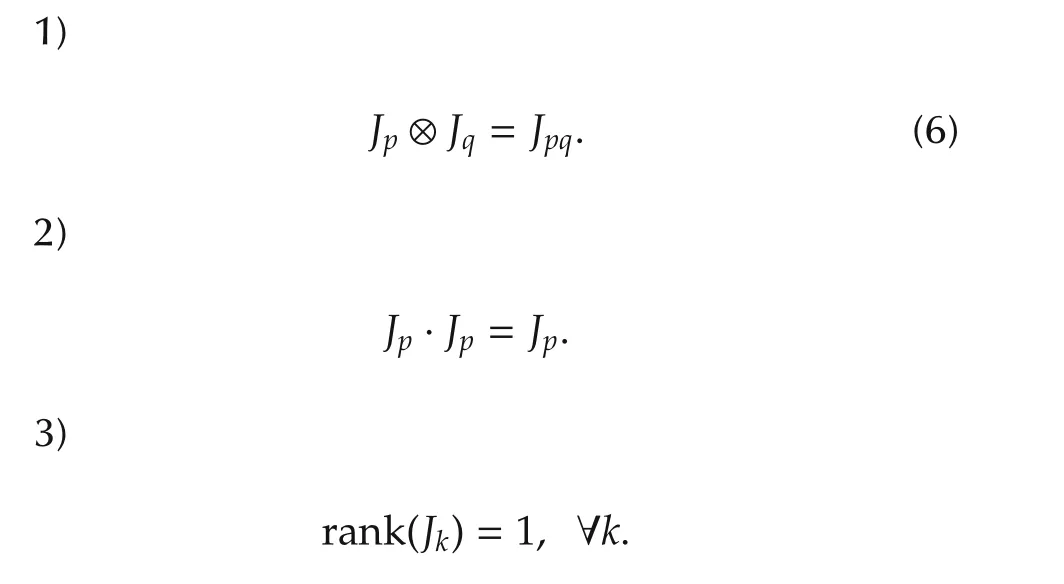
4)Jkhas only one non-zero eigenvalue,which is 1.

5){Jk|k∈N}is a monoid with identity J1=1.

Note that a set G with a binary operation＊:G×G→G,denoted by(G,＊),is a monoid,if it is a semigroup with identity[7].

We list some properties of STP-II without proof.Because they are similar to the corresponding ones of STP,only by replacing Ikby Jk.Then their proofs are almost the same as for STP except some obvious modifications.

Proposition 2 Next,° can be either°ιor°r.

1)(Associativity)

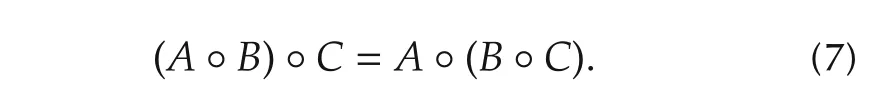
2)(Distributivity)

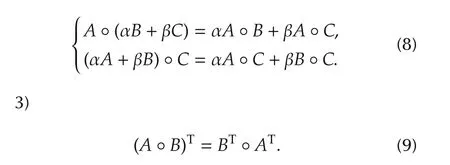
Proposition 3 Let A ∈ Mm×nand B ∈ Mp×q.Then the left STP-II of A and B can be alternatively defined as

where

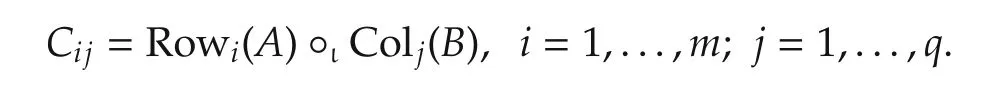
However,this is not true for°r.

Remark 1 Denote the set of all matrices as

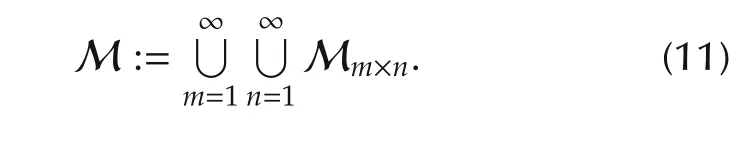
It is easy to verify that(M,°)is a semi-group.However,unlike(M,▷◁),(M,°)is not a monoid,because 1°A ≠ A.The scalar product and▷◁are consistent,but the number product and°are not consistent.This is a big difference between(M,°)and(M,▷◁).(Note that similar to °,▷◁can be either or).

3 STP-II equivalence

Similarly to STP-I,one sees easily that STP-II is basically also a product of two equivalence classes{A,A°J1,A°J2,...}with{B,B°J1,B°J2,...}.Motivated by this,we give the following equivalence relation.

Definition 3

.A,B∈M are said to be left STP-II equivalent,denoted by A ≈ιB,if there exist Jαand Jβ,such that

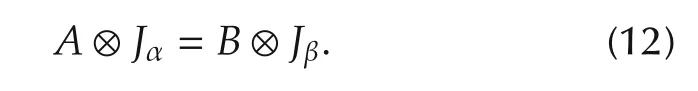
.A,B∈M are said to be right STP-II equivalent,denoted by A ≈rB,if there exist Jαand Jβ,such that

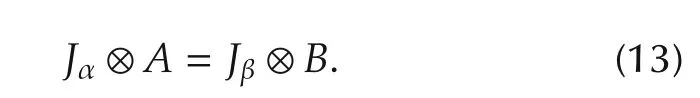
.The left STP-II equivalent class is denoted by

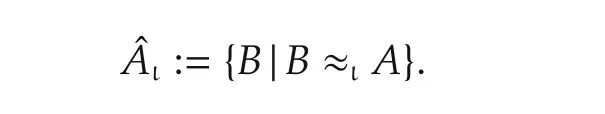
.The right STP-II equivalent class is denoted by

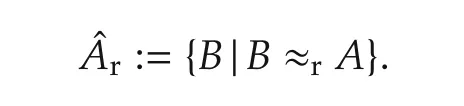
Denote by

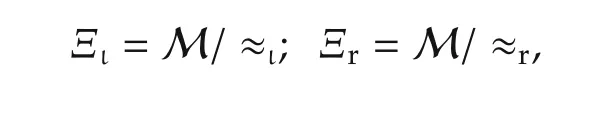
which are the set of left,right STP-II equivalence classes respectively.

It is ready to verify that the relations defined by(12)and(13)are equivalence relations,(i.e.,both of them are reflexive,symmetric,and transitive[8]).

Let A be a square matrix.Then it is ready to check that

Hence,we can define the trace on an equivalence class as follows.

Definition 4 Consider an equivalence class of square matrixA,which is eitherAιorAr.A trace is defined by

4 Lattice structure on equivalence class

For statement and notational ease,hereafter°is understood as°ιand≈is understood as≈ι.Then we do not need to repeat similar statements twice.With obvious modification one sees easily that°could be understood as for both °ιand °r.

Definition 5[9] Let L be a partial ordered set.If for any two elements a,b∈L there exist a lowest upper bound sup(a,b)∈L and a greatest lower bound inf(a,b)∈L,then L(with the order)is called a lattice.

Definition 6 Assume A≈B and there exists Jk,k?1,such that A⊗Jk=B,then

1)A is called a divisor of B and B is called a multiple of A;

2)an order can be defined as A≺B.This order makes M a partial order set.

Proposition 4 Assume A≈B,and hence(12)holds.If in(12)α∧β=1.Define

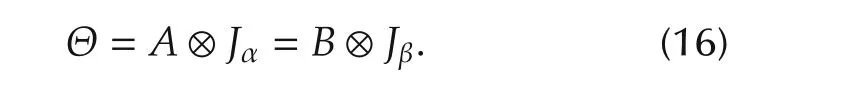
Then Θ =sup(A,B).That is, Θ is the least common multiple of A and B.

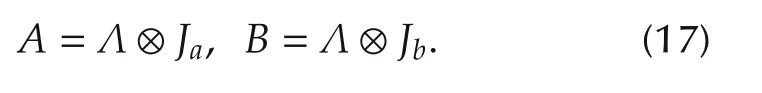
Proposition 5 Assume A≈B.Then there exists a Λ,such that Assume a∧ b=1,then Λ =inf(A,B).That is,Λ is the greatest common divisor of A and B.

Propositions 4 and 5 assure the following lattice structure.

Corollary 1 LetA∈Ξ.Then(A,≺)is a lattice.

In previous Corollary 1A could be eitherAιorAr.Then Ξ is either Ξιor Ξr.Hence,we have two kinds of lattices:(Aι,≺ι)and(Ar,≺r).

Remark 2 The following results about STP-I equivalence are well known[10].

1)A,B∈M is said to be STP equivalent,denoted by A ∼ B,if there exist Iαand Iβsuch that

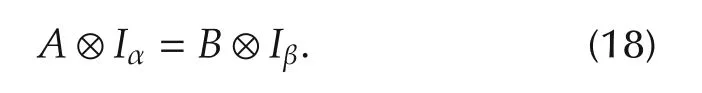
The equivalence class is denoted by

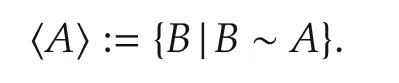
2)A partial order≺of M is defined as follows:A≺B,if there exists Iksuch that A⊗Ik=B.

3)Assume(18)holds and α ∧β =1,set

Θ :=A ⊗ Iα=B ⊗ Iβ.

Then Θ=sup(A,B).

4)Assume A ∼ B,then there exists a Λ ∈ M,such that

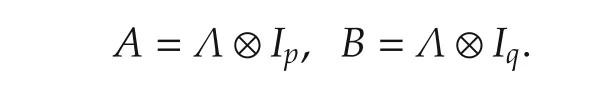
If p∧q=1,then Λ is unique.Moreover,Λ =inf(A,B).

We summarize that(〈A〉,≺)is a lattice.

All the above statements have been proved in[10].As the Ik’s being replaced by Jk’s,all the proofs remain available.Therefore,we skip the proofs for Propositions 4,5,and Corollary 1.

Proposition 6 Let(〈A〉,≺)and(B,≺)be two lattices.Then(〈A〉,≺)and(B,≺)are isomorphic lattices.

Proof Let A1∈〈A〉and B1∈B be the root elements of〈A〉andB respectively.Define φ:〈A〉→B as follows:

It is ready to verify that φ is a lattice isomorphism.

5 Vector space structure

Define

Then we have a partition as

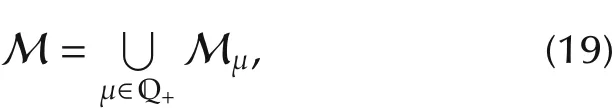
where Q+is the set of positive rational numbers.Correspondingly,we also set

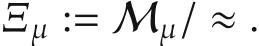
Then we also have a partition for the quotient space as

Our purpose is to pose a proper vector space structure on each Mμand Ξμ.

Definition 7[11] Let X be a set.Suppose there is a mapping(x,y)→ x+y of X × X into X,called addition,and a mapping(a,x)→ ax of R×X into X,called scalar multiplication,such that the following axioms are satisfied(x,y,z denoting arbitrary elements of L,and a,b arbitrary elements of R):

1)(x+y)+z=z+(y+z),

2)x+y=y+x,

3)There exists a unique element 0∈X,such that x+0=x for all x∈X,

4)For each x∈X,there exists unique z=-x∈X such that x+z=0,

5)a(x+y)=ax+ay,

6)(a+b)x=ax+bx,

7)a(bx)=(ab)x,

8)1x=x,

then X is called a vector space.

Definition 8 Assume X with addition“+”and scalar multiplication “·”satisfies all the requires for a vector space except that the zero is a set,hence for each x∈X the inverse-x may not unique.Then X is called a pseudo-vector space.

Definition 9 Let A,B ∈Mμ.Precisely,A ∈Mm×n,B ∈ Mp×q,and m/n=p/q= μ.Set t=m∨p.Then,

1)the left M-II matrix addition of A and B,denote by+ι,is defined as

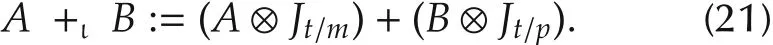
Correspondingly,the left M-II matrix subtraction is defined as

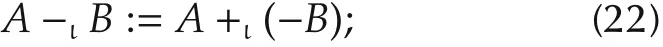
2)the right M-II matrix addition of A and B,denote by+r,is defined as

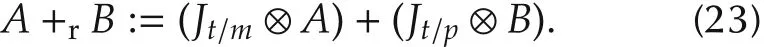
Correspondingly,the right M-II matrix subtraction is defined as

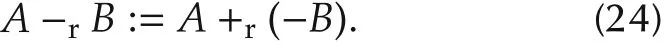
Remark 3 If in the above definition all Jk’s are replaced by corresponding Ik’s,the M-II matrix addition/subtraction becomes M-I matrix addition/subtraction,which have been discussed in detail in[10].

Remark 4 Let σ ∈ {+ι,-ι,+r,-r}be one of the four binary operators.Then it is easy to verify that

1)if A,B∈Mμ,then AσB∈Mμ;

2)if A and B are as in Definition 9,then AσB ∈

3)set s=n∨q,then s/n=t/m and s/q=t/p.Therefore,σ can also be defined by using column numbers respectively,e.g.,

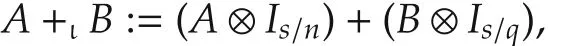
etc.

It is easy to verify the following conclusion.

Proposition 7 Mμwith addition(+ιor+r)and conventionalscalarproductis a pseudo-vectorspace,where for each A,its inverse is defined as

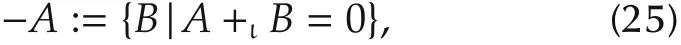
which is not unique.

In fact,it is easy to verify that A+ιB=0,if and only if,A ≈ιB,(or A+rB=0,if and only if,A ≈rB).Then when the quotient space is considered,we have a vector space.

Definition 10 LetA,B∈Ξ.Then,

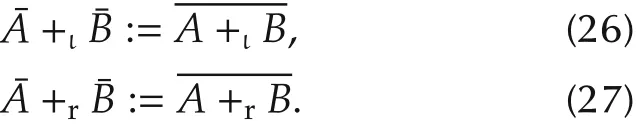
Correspondingly,

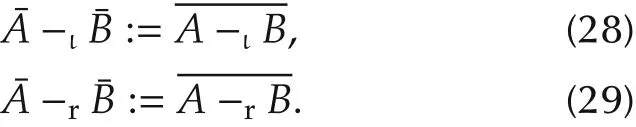
It is easy to verify that(26)(or(27))and(28)(or(29))are properly defined.Thatis,they are independentofthe choice of representatives A∈A and B∈B.Moreover,the scalar product can be properly defined by

Finally,we have the following result:

Proposition 8 Ξμwith addition defined by(26)(or(27))and scalar product defined by(30)is a vector space.

6 Metric and metric topology

Let A=(ai,j),B=(bi,j)∈ Mm×n.It is well known that the Frobenius inner product of A and B is defined by

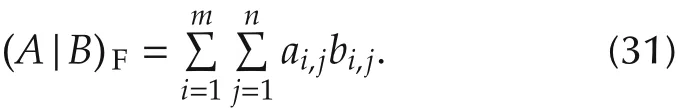
The Frobenius norm is defined by

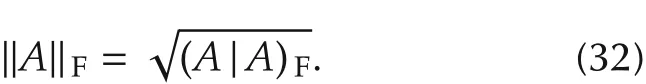
Now inside each Mμwe assume μy,μx∈ N are coprime and μy/μx= μ.Then,

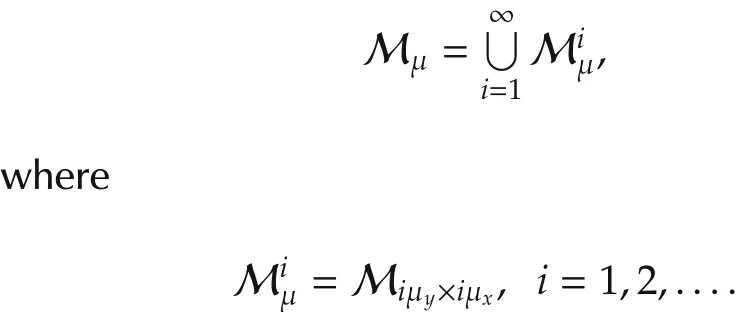
Definition 11 Let A,B ∈ Mμ,where A ∈ Mαμand B ∈ Mβμ.Then,

1)the left STP-II inner product of A,B is defined by

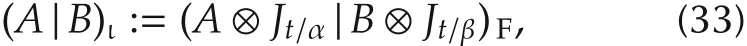
where t= α ∨ β is the least common multiple of α and β;

2)the left STP-II norm of A is defined by

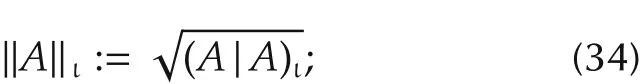
3)a left STP-II matric(distance)of A and B is defined by

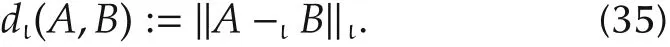
The corresponding right STP-II inner product,right STP-II norm,and right STP-II matric(distance)can be defined similarly.

The following proposition is easily verifiable.

Proposition 9 Mμwith distance defined by(35)is a pseudo-metric space.

Remark 5 Mμwith distance defined by(35)is not a metric space.It is easy to verify that dι(A,B)=0,if and only if,A ≈ιB.

Next,we consider the quotient space.We need the following lemma,which comes from a straightforward computation.

Lemma 1 Let A,B ∈ Mm×n.Then

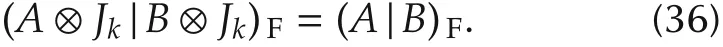
Using Lemma 1 and Definition 11,we have the following property.

Proposition 10 Let A,B∈Mμ,if A and B are orthogonal,i.e.,(A|B)F=0,then A⊗ Jξand B⊗ jξare also orthogonal.

Now we are ready to define the inner product on Ξμ.

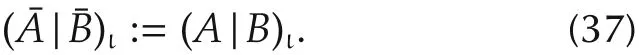
The following proposition shows that(37)is well defined.

Proposition 11 Definition 12 is well defined.That is,(37)is independent of the choice of representatives A and B.

Proof Assume A1∈A and B1∈B are irreducible.Then it is enough to prove that

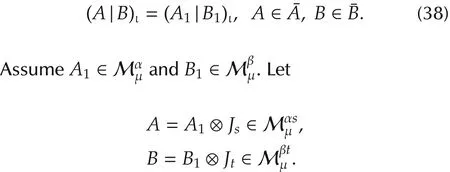
Denote by ξ = α∨β,ξη = αs∨βt.Using(36),we have

Definition 13[12] A real vector space X is an innerproductspace,ifthere is a mapping X×X→R,denoted by(x|y),satisfying

By definition it is easy to verify the following result.

Theorem 1 The vector space(Ξμ,+ι)with the inner product defined by(37)is an inner product space.

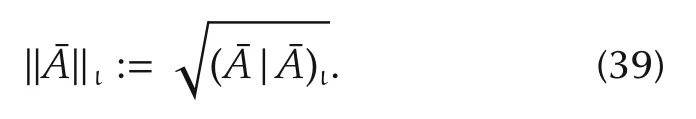
The following is some standard results for inner product space.

1)(Schwarz inequality)

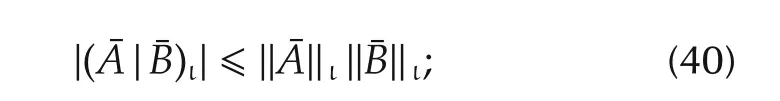
2)(Triangular inequality)

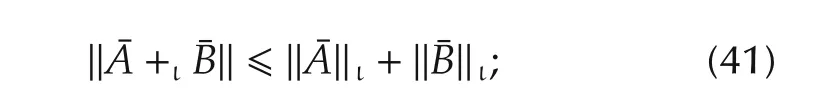
3)(Parallelogram law)

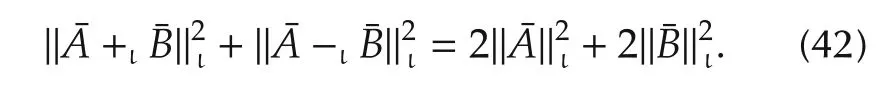
Note that the above properties show that Ξμis a normed space.

Finally,we present the generalized Pythagorean theorem.

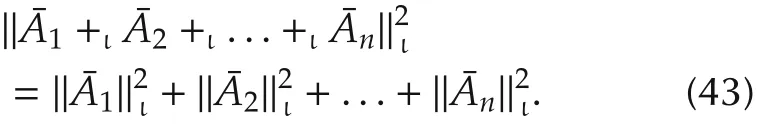
Remark 6 All the results in this section have their corresponding results for right STP-II equivalence.Precisely speaking,we have

.Let A,B ∈ Mm×n.Then their right STP-II inner product is defined as

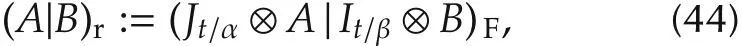
where t=α∨β.

.LetAr,Br∈Ξμ.Their inner product is defined as

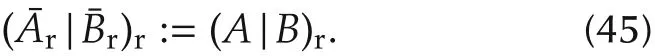
.The vector space(Ξμ,+r)with the inner product defined by(44)is an inner product space,but not a Hilbert space.

.The norm ofAr∈Ξμis defined as

7 Metric and metric topology on Ξμ

Using the norm defined in previous section one sees easily that Ξμis a metric space.

Theorem 4 Ξμwith distance

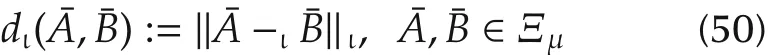
is a metric space.

Using this metric,the metric topology is obtained,which is denoted by Td.

Consider

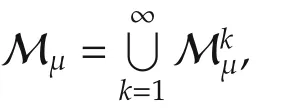
a natural topology can be constructed as follows:

1)each Mkμis a clopen set;

2)on each Mkμ,a naturalEuclidean topology of Rk2μyμxis posed.

Now we consider a natural projection Pr:Mμ→Ξμdefined by

Similarly to STP-I equivalence case,by using projection Pr,two topologies ofΞμcan be obtained,which are product topology TPand quotient topology TQ.Again a similar argument as for STP-I equivalence,we have the following result,which is exactly the same as for STP-I equivalence case.

Theorem 5 Consider Ξμ.The metric topology determined by the distance dιis denoted by Td.Then,

8 Subspaces of Ξμ

Consider the k-upper bounded subspacewhich is defined as

We have

Proposition 13[13] Let E be an inner product space,{0}≠F⊂E be a Hilbert subspace.

1)For each x∈E there exists a unique y:=PF(x)∈F,called the projection of x on F,such that

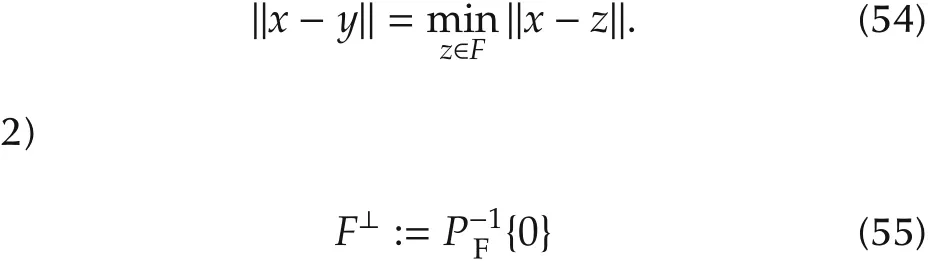
is the subspace orthogonal to F.

where⊕stands for orthogonal sum.

Using above proposition,we consider the projection:PF:Ξμ→Ξ[·,α]μ.LetA∈Ξβμ.AssumeX∈Ξαμ,t=α∨β.Then the norm ofA-ιX is

It is easy to verify the following result:

Proposition 14 1)Assume PF(A)=C,where A=(Ai,j)is defined by(58)and C=(ci,j)is defined by(59).Then

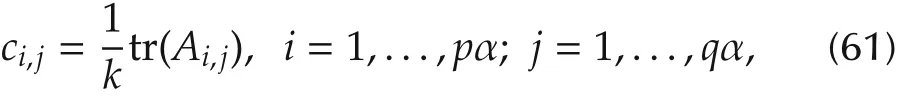
where tr(A)is the trace of A.

2)The following orthogonality holds:

9 Conclusions

In this paper a new matrix product,called the second STP(STP-II,or it also called MM-II product)of matrices,is proposed.To build the theory of STP-II,its properties and various geometric structures have been investigated.First,some fundamental properties are presented.Second,the STP-II caused equivalence is proposed.Based on this equivalence,the corresponding quotient space is constructed.Then the vector space structure,inner product,and the metric are all obtained.Finally,as an inner product space,some subspaces of the quotient space with orthogonal projections are considered.In own word,the quotient space has been investigated in detail.

We expect that the second STP may receive more and more applications as those of the first STP.