Event-triggered state estimation for T-S fuzzy affine systems based on piecewise Lyapunov-Krasovskii functionals

Meng WANG ,Jianbin QIU ,Gang FENG †

1.Department of Biomedical Engineering,City University of Hong Kong,Kowloon,Hong Kong,China;

2.State Key Laboratory of Robotics and Systems&Research Institute of Intelligent Control and Systems,Harbin Institute of Technology,Harbin Heilongjiang 150080,China

Received 3 September 2018;revised 4 October 2018;accepted 8 October 2018

Abstract This paper investigates the problem of event-triggered H∞state estimation for Takagi-Sugeno(T-S)fuzzy affine systems.The objective is to design an event-triggered scheme and an observer such that the resulting estimation error system is asymptotically stable with a prescribed H∞performance and at the same time unnecessary output measurement transmission can be reduced.First,an event-triggered scheme is proposed to determine whether the sampled measurements should be transmitted or not.The output measurements,which trigger the condition,are supposed to suffer a network-induced time-varying and bounded delay before arriving at the observer.Then,by adopting the input delay method,the estimation error system can be reformulated as a piecewise delay system.Based on the piecewise Lyapunov-Krasovskii functional and the Finsler’s lemma,the event-triggered H∞observer design method is developed.Moreover,an algorithm is proposed to co-design the observer gains and the eventtriggering parameters to guarantee that the estimation error system is asymptotically stable with a given disturbance attenuation level and the signal transmission rate is reduced as much as possible.Simulation studies are given to show the effectiveness of the proposed method.

Keywords:Takagi-Sugeno(T-S)fuzzy affine systems,event-triggered scheme,piecewise Lyapunov-Krasovskii functional,state estimation

1 Introduction

During the past few decades,the fuzzy-logic-control(FLC)has attracted great research attention,because it is a simple and powerful tool for analysis and synthesis of many complex nonlinear control systems[1-3].Among various model-based fuzzy control systems,the Takagi-Sugeno(T-S)fuzzy model has been well studied in recent years(please see[4-11]and reference therein).It has been shown that T-S fuzzy models can accurately approximate any smooth nonlinear functions in any compact set[12-14].The most appealing characteristic of the T-S fuzzy model is that it is a combination ofa numberoflinear/affine systemssmoothly connected by fuzzy membership functions so that analysis and synthesis of complex nonlinear systems can be carried out based on the fruitful linear systems theory.

On the other hand,recent years have also witnessed growing research interests in networked control systems(NCSs).Compared with traditional control systems,there are some advantages of NCSs,for example,low cost,simple installation,and easy reconfigurability[15-18].Because of their advantages,the NCSs have been widely applied to many fields,such as power systems,manufacturing plants,and chemical processes,etc.[19,20].However,the introduction of communication networks in NCSs also brings some constraints for system stability analysis and synthesis.For example,if there are a large number of redundant sampled signals released to a shared communication network with limited bandwidth,it inevitably causes a congested network traffic.Therefore,in NCSs,the conventional time-triggered or time-driven control strategies may not be desirable.Recently,there appeared some works on event-triggered control for networked-based systems with constraints of limited network bandwidth and transmission delays.To mention a few,in[21,22]the event-triggered conditions were based on instantaneous system states.Hence,extra hardware is required to monitor the system state continuously.In[23],the decentralized event-triggered control was investigated by modeling the event-triggered control systems as impulsive models.In[24],the so-called periodic eventtriggered control strategy was developed,where the event-triggered condition was verified at every sampling instant to decide whether or not to transmit the newly sampled measurements.The event-triggered control strategy was also adopted to deal with several control issues for T-S fuzzy systems,such as reliable control[25,26],robust control[27],and sliding-mode control[28].Event-triggered control has also been widely adopted for multi-agent systems[29-33].

However,all the aforementioned works focus on problems of the stability analysis and controller synthesis.The problem of event-triggered state estimation for dynamic systems also deserves investigation.There are a few results on the observer design problem under event-triggered schemes,especially for T-S fuzzy systems[34-38].However,it is worth noting that all the results obtained by[35,37,38]were based on common Lyapunov functionals,which tends to be conservative.Also note that most of the observer design results were obtained only for T-S fuzzy systems with linear local models,while,it has been shown that a T-S fuzzy affine dynamic model with affine terms has much improved approximation capacities[12,39].The analysis and synthesis procedures for T-S fuzzy affine systems are generally more complicated than T-S fuzzy linear systems.To the authors’best knowledge,few attempts have been made on an event-triggered state estimation for T-S fuzzy affine systems based on piecewise Lypapunov-Krasovskii functionals,which motivates us for this study.

In this paper,we investigate the problem of eventtriggered H∞state estimation for T-S fuzzy affine systems.The objective is to design an event-triggered scheme and an observer such that the resulting estimation error system is asymptotically stable with a prescribed H∞performance and at the same time unnecessary output measurement transmission can be reduced.First,an event-triggered scheme is proposed to determine whether the sampled measurements should be transmitted or not.The output measurements which trigger the condition suffer a network-induced timevarying and bounded delay before arriving at the observer.Then,by adopting the input delay method,the estimation error system can be reformulated as a piecewise delay system.Based on the piecewise Lyapunov-Krasovskiifunctionaland the Finsler’s lemma,the eventtriggered H∞observer design method is developed.Moreover,an algorithm is proposed to co-design the observer gains and the event-triggering parameters to guarantee that the estimation error system is asymptotically stable with a given disturbance attenuation level and the signal transmission rate is reduced as much as possible.

Notation Rnrefers to n-dimensional Euclidean space.Snrefers to the set of n×n real symmetric positive definite matrices.The notation N refers to positive integers.Matrix Q＞0 means that Q is positive definite.0q×pand Iprefer to the q×p zero matrix and p×p identity matrix,respectively.The notation⋆in a matrix refers to the terms,which can be induced by symmetry.diag{···}denotes the block-diagonal matrix.Sym{Q}is the shorthand notation for Q+QT.l2[0,∞)denotes the space of square-summable infinite vector sequences over[0,∞).

2 Model description and problem formulation

2.1 Continuous-time piecewise fuzzy affine model

Consider a continuous-time Takagi-Sugeno(T-S)fuzzy affine model described by the following IF-THEN rules:

where Fldenotes the l th fuzzy inference rule;r is the number of inference rule;Flφ(φ=1,2,...,s)are fuzzy sets;x(t)∈Rnxis the system state;y(t)∈Rnyis the measured output;z(t)∈Rnzis the signal to be estimated;w(t)∈Rnwand v(t)∈Rnvare the disturbance input and the measurementnoise,respectively,which both belong to l2[0,∞).η(x(t)):=[η1(x(t)),η2(x(t)),...,ηg(x(t))]are premise variables of the system,which are not necessarily measurable.Al,al,Bl,and Llare known constant system matrices of the l th local model,and C,D are two known constant system matrices.ΔAland Δaldenote the uncertain terms of the l th local model,which can be written as the following form

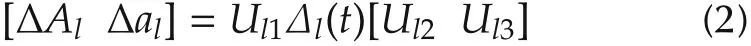
with Ul1,Ul2,and Ul3being the known real constant matrices of appropriate dimensions.Δl(t)∈ Rp1×p2are unknown matrix functions subject to

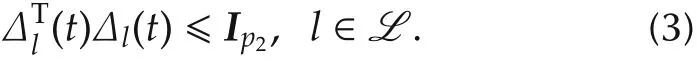
The parameter uncertainties are said to be admissible if(2)and(3)hold.

Let μl[η(x(t))]denote the normalized membership function of the inferred fuzzy set F

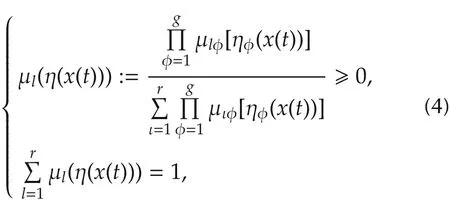
where μlφ[ηφ(x(t))]is the grade of membership of ηφ(x(t))in.In the sequel,we will drop the argument of μl(η(x(t)))for clarity,i.e.,denote μl(η(x(t)))as μl.

By using a center-average defuzzifier,product inference and singleton fuzzifier,the fuzzy affine dynamic model(1)can be expressed globally by the following form:

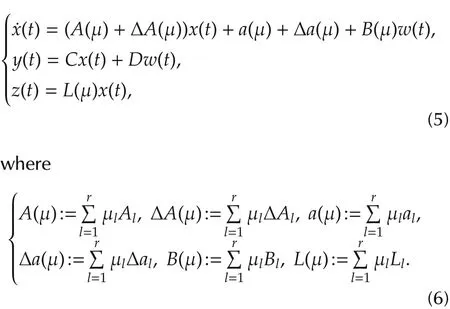
In thispaper,the state spaces are decomposed into crisp subspaces and fuzzy subspaces.The crisp subspace denotes the region where μl[η(x(t))]=1 for some l,and all other membership functions are inactive,which indicates that the system dynamics are only governed by the l th local model of the fuzzy system(1).The fuzzy subspace refers to the region where 0 ＜ μl[η(x(t))]＜ 1,and the system dynamics are thus characterized by a convex blending of two or more local models.Use a set I to represent region indexes.And in each region Si,i∈I,define the set I(i)as

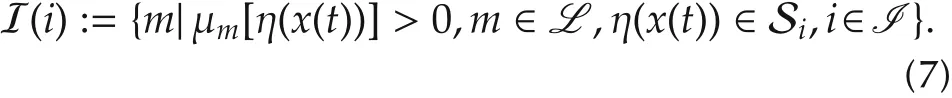
The set I(i)indicates that it contains the indexes for the system matrices,which are used in the interpolation within that subspace.The global T-S fuzzy-affinedynamic model(5)can be rewritten as a blending of s∈I(i)subsystems

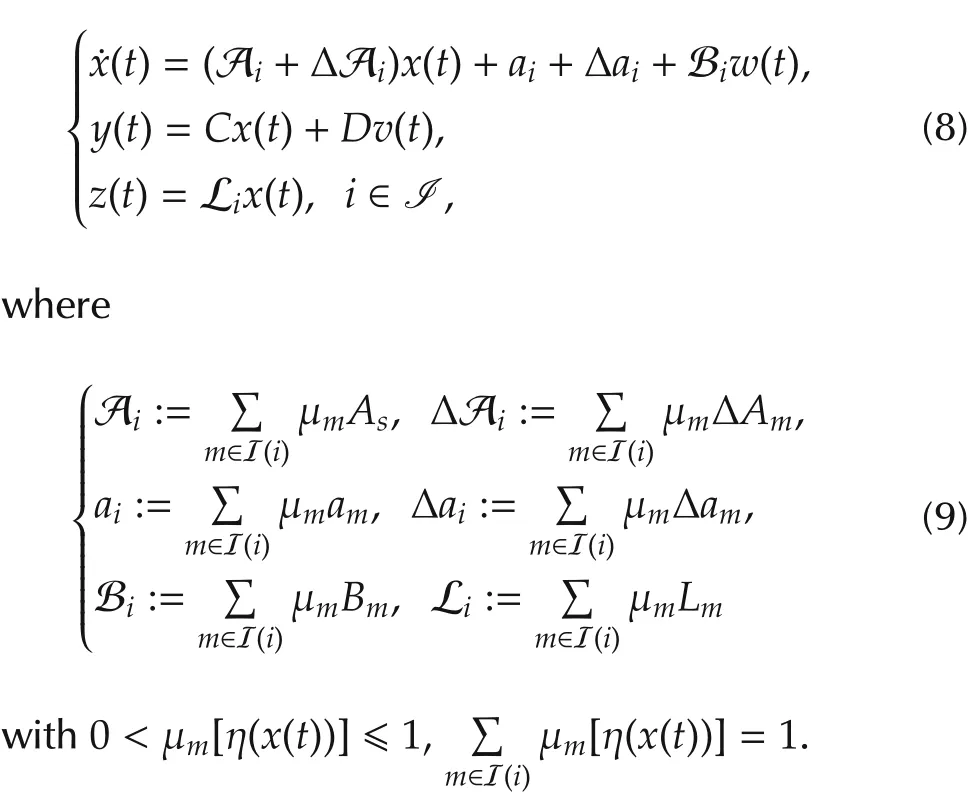
2.2 Event-triggered scheme

In order to save the communication resources with limited network bandwidth,an event-triggered scheme(ETS)is introduced forthe observerdesign.Itis assumed that sensors are time-triggered with a constant sampling period h.Then,the sampling output measurements can be denoted by y(kh),k∈N.Assuming that the latest successfully transmitted output measurement is tkh(tkis positive integers),the next transmission instant can be expressed as

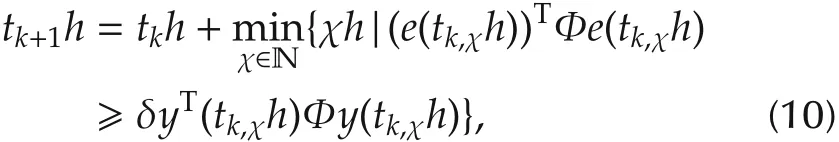
where tk,χh=tkh+ χh,e(tk,χh)=y(tk,χh)-y(tkh),and δ?0(threshold),Φ＞0 being event-triggered parameters to be designed.

Considering the network-induced transmission delay,the output measurement y(tkh)will be successfully received by the observer at instant tkh+τtk,where the delay τtksatisfies τtk? τM.The input to the observer,i.e.,y(tkh)will be kept constant during t∈Ω:=[tkh+ τtk,tk+1h+ τtk+1).The holding interval Ω can be divided into sampling-interval-like subsets

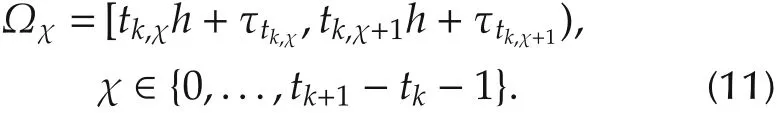
To facilitate the state observer design,an input delay method is adopted in this paper.First,the instant tk,χh can be rewritten as in the following time-delay form:

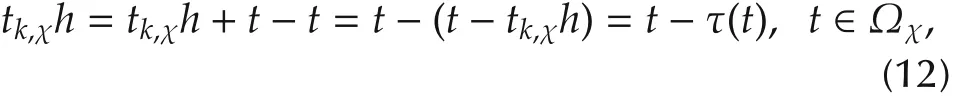
where τ(t):=t-tk,χh,0?τ(t)?h+τM=τ.

Therefore,during the time interval Ωχ,χ ∈ {0,1,...,tk+1-tk-1}the input of the observer can be expressed as

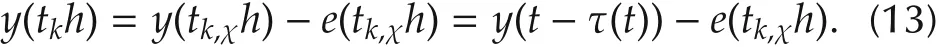
In addition,the event-triggering condition in(10)is not satisfied during the interval t∈Ωχ,χ ∈{0,1,...,tk+1-tk-1},that is,

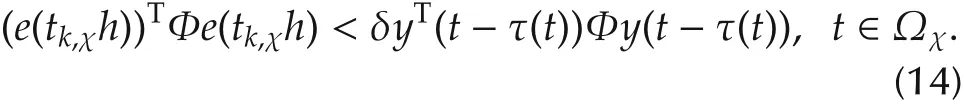
Remark 1 Note that the threshold δ plays an important role in the event-triggered condition(10).When a bigger δ is chosen,the condition(10)will be harder to satisfy and less events will be triggered.In another special case,δ is chosen as zero,the condition(e(tk,χh))TΦe(tk,χh)? δyT(tk,χh)Φy(tk,χh)in(10)will be satisfied automatically,which means,all the sampled output measurements will be transmitted to the observer.The system investigated will reduce to a sampled-data system.

Remark 2 It is assumed that the network-induced delay is constant in[40]and bounded by the sampling period h in[41],respectively.However,in practical situation the delay may be time-varying and exceed the sampling period.Therefore,this assumption restricts the application of the event-triggered based filtering and control methods developed in[40,41],respectively.In this paper,it is assumed that the network-induced delay is bounded by τM,which can be longer than the sampling period h.

2.3 Piecewise fuzzy affine observer

Given the uncertain T-S fuzzy affine dynamic system(8)in each region,we consider the following piecewise fuzzy affine observer:

Region rule s:IFx(t)∈SsTHEN

Local observer rule Rn:

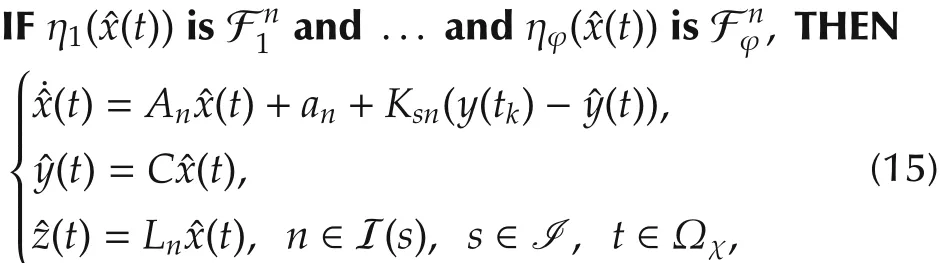
wherex(t)∈Rnxis the estimated state,z(t)∈Rnzis the estimation of signal z(t),and Ksn∈ Rnx×nyare appropriately dimensioned observer gains to be determined.

Similarly,the overall piecewise fuzzy affine observer is inferred as follows:

wherex(t):=x(t)-x(t).

Combining system(8)and the observer(15)yields the following estimation error system:

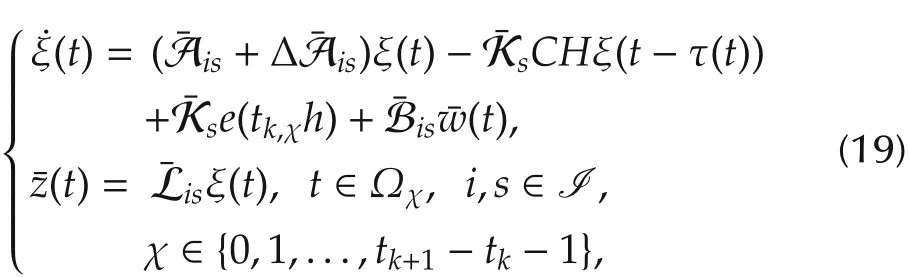
where

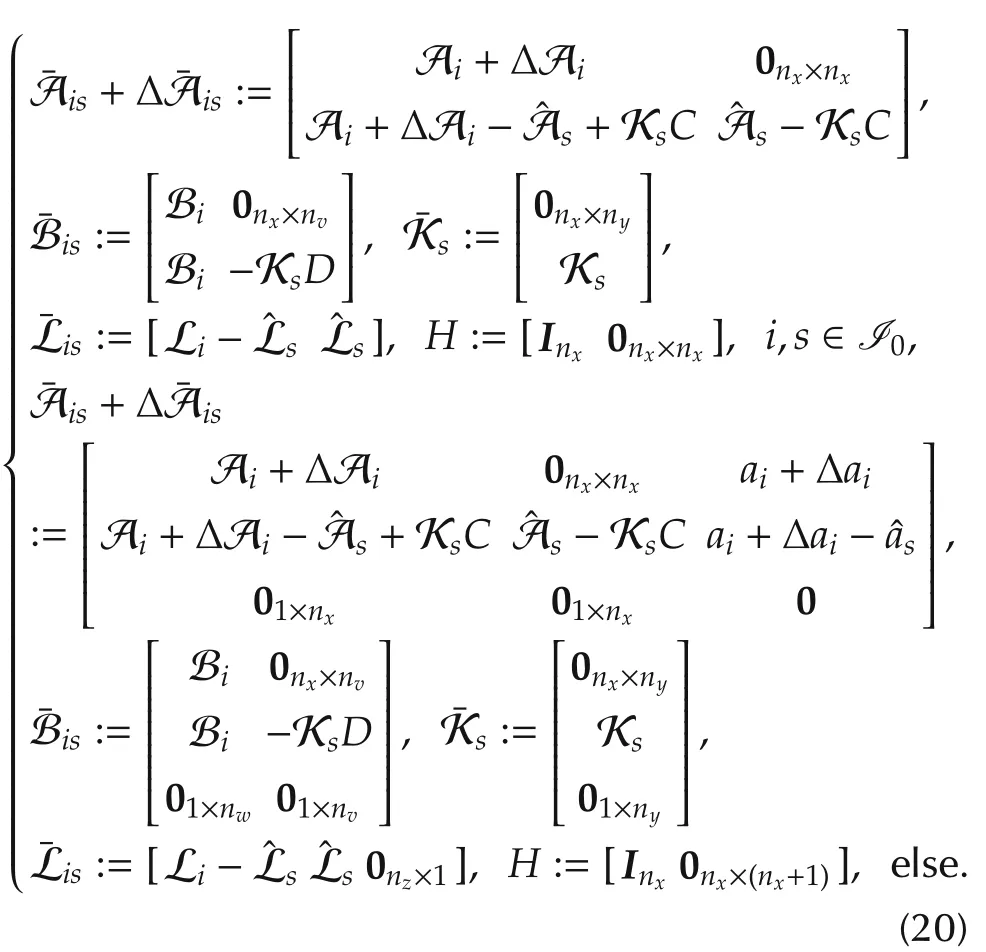
Then,the problem of event-triggered H∞state estimation for T-S fuzzy affine systems to be investigated in this paper now can be summarized as follows.

Under the ETS(10),design an observer of the form(15)for the T-S fuzzy affine system(8),such that

i)The resulting estimation error system(19)withw(t)=0 is asymptotically stable;

ii)Under zero initial conditions,the prescribed H∞performance γ is guaranteed,i.e.,

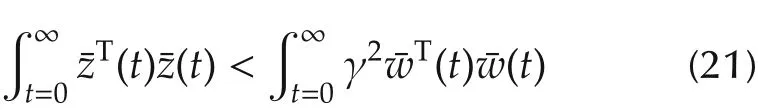
holds for all nonzerow(t)∈l2[0,∞).In this case,system(19)is said to be asymptotically stable with a guaranteed H∞performance γ.

Remark 3 Since there exist the event-triggered scheme and the networked-induced transmission delay between the plant and the observer,the premise variable η(x(t))of the system can not be utilized on the observer side.To overcome this difficulty,in this paper,the premise variables of the observer are determined by the estimated states instead of the states of the system.

3 Main results

To ensure the continuity of piecewise Lyapunov-Krasovskii functional across the region boundaries,one can constructthe matrices Fi∈ Rnf×nx,fi∈ Rnf×1,i∈ I,

with fi=0 for i∈I0,which satisfy the following boundary conditions:

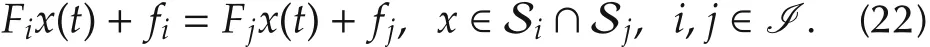
Similarly,for the observer(15),the following boundary conditions are also satisfied

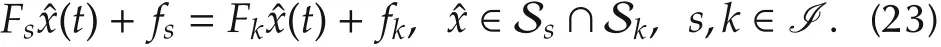
With the matrices Fiand fi,i∈I,one can obtain the continuity matrices in each regions for the estimation error system(19)

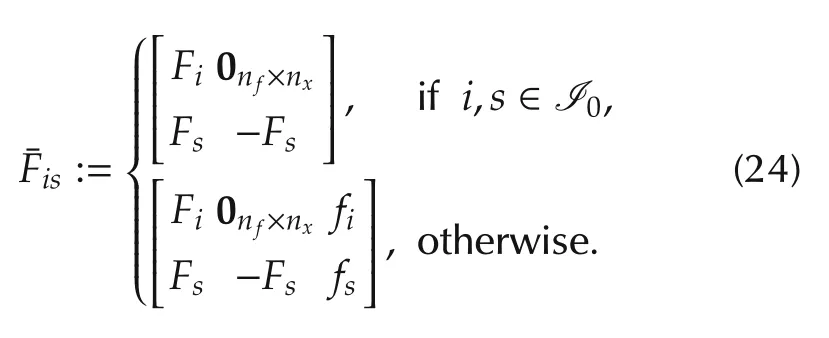
For the boundaries of the states of the estimation error system(19),i.e.,x(t)∈Si∩Sjandx(t)∈Ss∩Sk,i,s,j,k∈I,one has

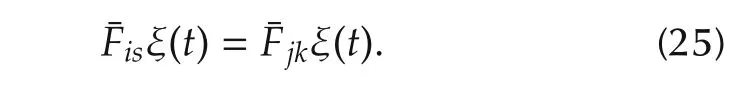
In addition,for the purpose of conservatism reduction by the utilization of S-procedure,one can construct matrices Qi∈ Rnq×nxand qi∈ Rnq×1,i∈ I,with qi=0 for i∈I0such that

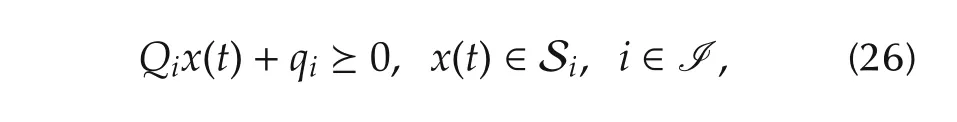
where the notation≥indicates that each entry of the vector is nonnegative.

For the observer(15),one also has

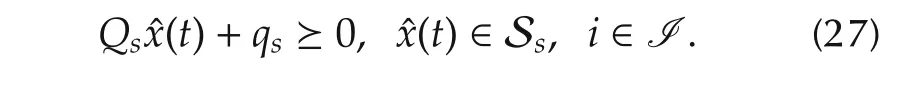
With the matrices Qiand qi,i∈I,one can obtain the matricesQis,i,s∈I

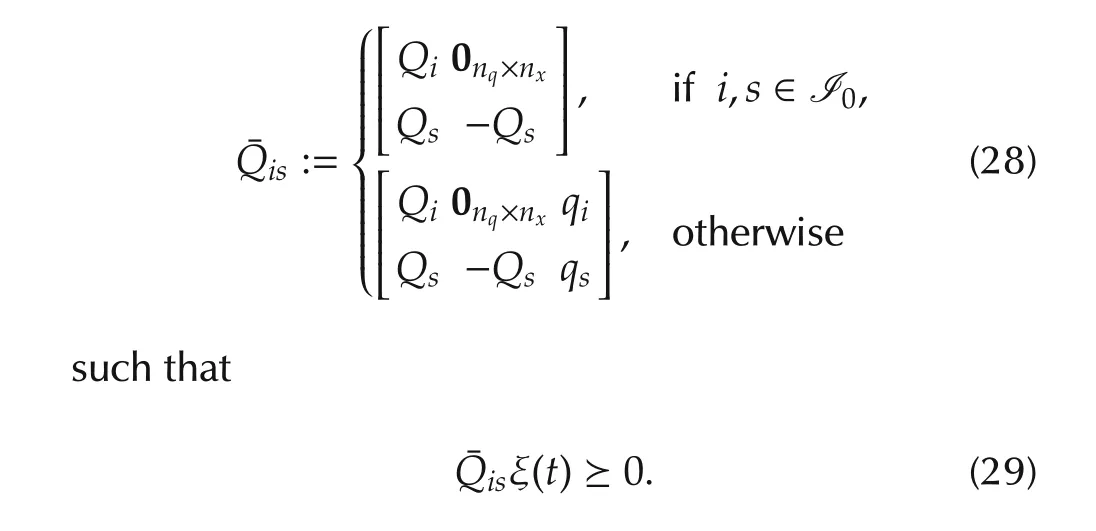
Now,the estimation performance analysis results will be presented in the following lemma.

Lemma 1 Consider system(8)and the observer(15).For given scalars＞0,δ?0 and γ ＞0,the estimation error system(19)is asymptotically stable with H∞performance γ under the ETC scheme(10),if there exist matrices P∈S2nf,R∈Snx,Z∈Snx,Φ∈Snx,0≤Wis=WiTs∈ R2ng×2ng,and Gis∈ Rσ×σ1,i,s ∈ I,such that the following matrix inequality holds:

Proof Consider the following piecewise Lyapunov-Krasovskiifunctional(PLKF)candidate forthe estimation error system(19),

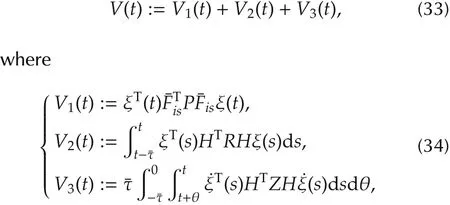
whereFisis defined in(24)and P,R,and Z being symmetry positive Lyapunov matrices to be determined.

Based on the PLKF given in(33),it is well known that it suffices to show the following inequality:

Note that during each subinterval Ωχ,the triggering condition(10)is not satisfied,that is,the inequality in(14)holds.It is easy to conclude that the following inequality implies(35):

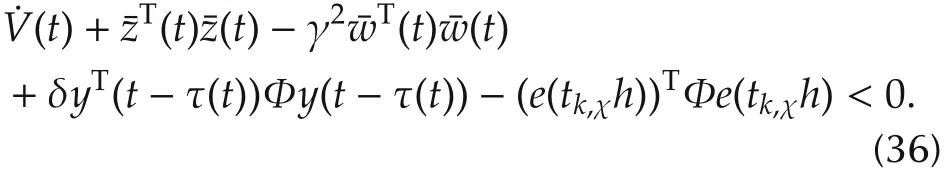
Taking the derivative of the PLKF V(t)along the trajectory of the estimation error system(19),the left-hand side(LHS)of inequality(36)can be rewritten as the following form:

Considering the structural partitioning information in(29)and utilizing S-procedure,together with(37)and(38),one has the following inequality implies(35)

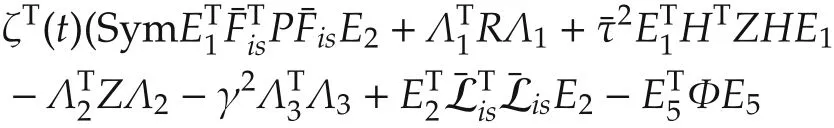
Now,applying Finsler’s lemma(shown in the appendix),one has that the condition(30)implies(35).The proof is thus completed.

Remark 4 Based on the PLKF(33),a novel H∞filtering performance analysis criterion for the estimation error system(19)is provided in Lemma 1.In[35,37,38],the common Lyapunov-Krasovskiifunctional(CLKF)was adopted to address the event-triggered filtering problem for T-S fuzzy systems.Compared with the common Lypunov functional method,our result is expected to be less conservative.

Based on the estimation performance analysis result,the synthesis result will be presented in the following theorem.

Theorem 1 Consider system(8)and the observer(15).For given scalarsτ＞0,δ?0 and γ ＞0,the estimation error system(19)is asymptotically stable with H∞performance γ,if there exist matrices P ∈ S2nf,R∈Snx,Z∈Snx,Φ ∈Snx,0≤Wis=WiTs∈ R2ng×2ng,Gis1∈ Rσ×nx,Gs2∈ Rnx×nx,i,s ∈ I,Gis3∈ Rσ×1,i∈I1∪s∈I1,Ksn∈Rnx×ny,s∈I,n∈I(s),and scalars ϵis＞ 0,i,s ∈ I,such that the following linear matrix inequality holds:

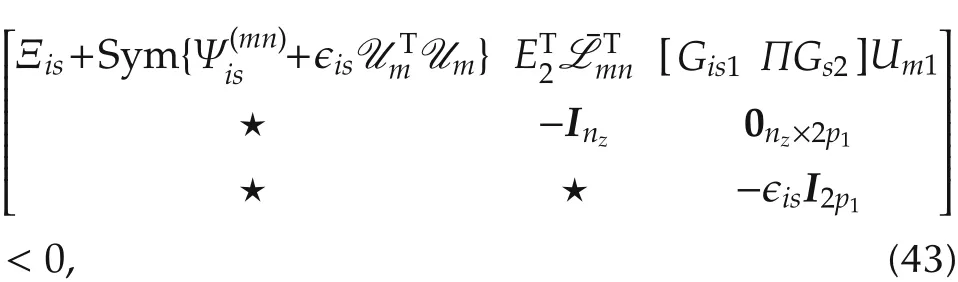
where i,s∈I,m∈I(i),n∈I(s),and

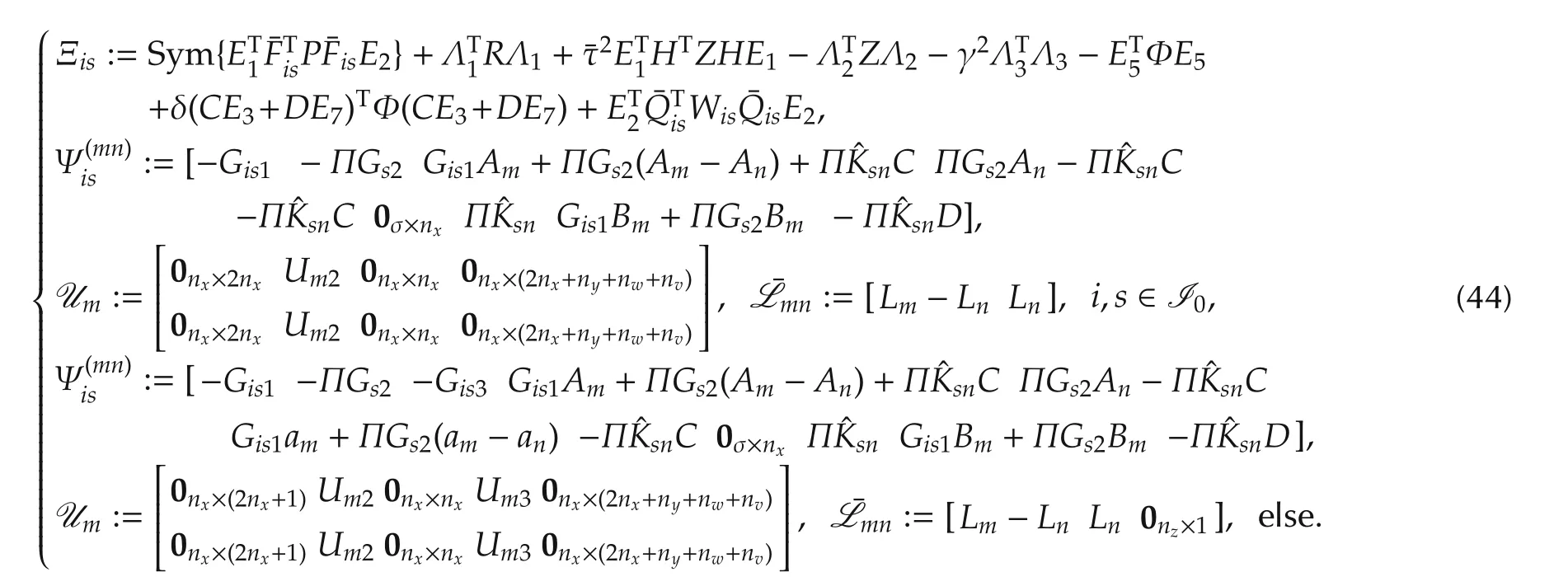
Moreover the observer gains can be obtained by

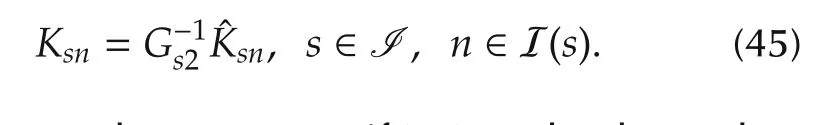
Proof Based on Lemma 1,if(30)can be shown then the claimed resultwillfollow.By Schurcomplement,the following inequality is equivalent to(30):

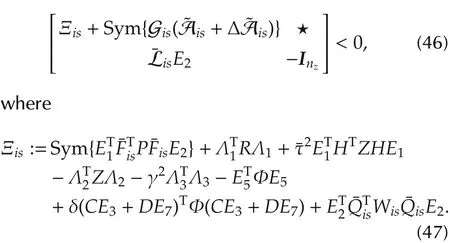
First,the matrix Giscan be constructed in the following form:

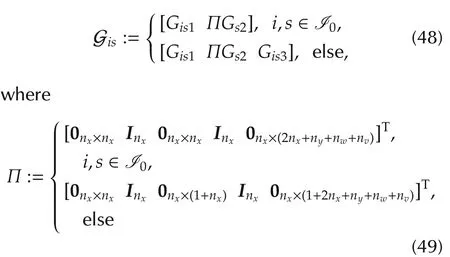
with Gis1∈ Rσ×nx,Gs2∈ Rnx×nx,and Gis3∈ Rσ×1being matrices to be designed.Notice that by the definition of the matrix Gisin the form of(48),the matrix variable Gs2can be absorbed by the observer gains Ksn,s∈I,n∈I(s)by defining On the basis of(9)and(17),the inequality(46)can be easily reorganized as

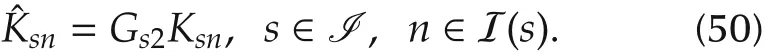
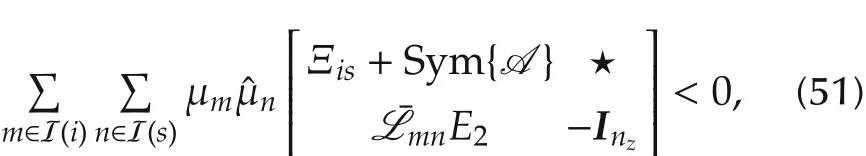
As the fuzzy membership functions are of intrinsically nonnegative property,one readily obtains that for i,s∈I,m∈I(i),n∈I(s)the following inequality implies(51):

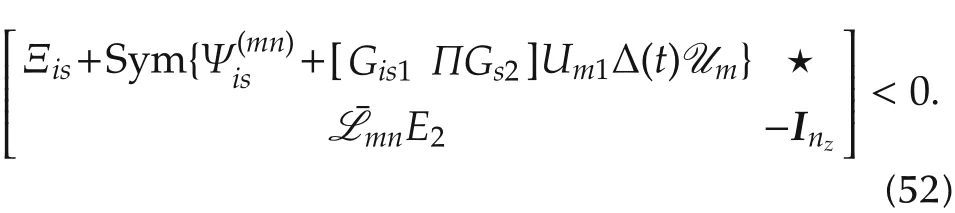
With the introduction of a set of scalars ϵis＞ 0,i,s∈I,one can obtain(43)by applying Lemma A2 shown in the appendix,to convexify the parameter uncertainties in(52).

In addition,the inequality(43)implies that-Gs2-＜0,which indicates that Gs2is a nonsingular matrix.Thus,one can obtain the observer gains from(45).The proof is thus completed.

Remark 5 The H∞state estimation performance analysis and observersynthesis results given in Lemma 1 and Theorem 1 are based on PLKF.If one sets[Fi|fi]=[Inx|0nx×1],i∈ I,the PLKF in(33)will reduce to CLKF,thus,the corresponding results in CLKF-based framework can be obtained.

It is worth mentioning that for given the eventtriggered threshold δ,the H∞performance index γ described in Theorem 1 can also be optimized,and the optimal index γmincan be obtained by the following convex optimization algorithm.

Algorithm 1 minγ,subject to linear matrix inequality(43).

Also note that in a real-world application,it is desirable to reduce the transmission rate as much as possible while the estimation error system is also guaranteed the asymptoticalstability with the prescribed H∞performance.To this end,the following algorithm is developed to co-design the event-triggered parameters(threshold δ and positive matrix Φ)and observer gains.

Algorithm 2 To find the maximized δ for given the prescribed H∞performance index γ ＞ 0.

Step 1 Set δ0=0 and a step length l ＞ 0,e.g.,l=0.001;

Step 2 Solve the linear matrix inequality in(43)with δ = δi,where δi= δi-1+l,i?1,δ0=0.

Step 3 If Sept(2)returns feasible solutions,then go to Step(2)with i=i+1;otherwise go to the next step;

Step 4 In this step δmax= δiis obtained.Solve the linear matrix inequality in(43)with δmaxto obtain feasible solutions with Φ and the observer gains obtained by(45),and stop.

Remark 6 It is a tradeoff between the H∞estimation performance γ and the signal transmission rate between the plant and the observer.That is,the more signals are transmitted the the observer,the better estimation performance index will be obtained.On the other hand,when the threshold δ is set zero,all the output measurements are successfully transmitted to the observer.In this case,by applying Algorithm 1 with δ=0,the obtainedis the smallest(best)performance index.It indicates that if the prescribed H∞performance γ＞in Algorithm 2,no δmaxand the corresponding observer gains will be obtained.

4 Simulation studies

Example 1 Consider a modified tunnel diode circuit system borrowed from[42,43],as shown in Fig.1.The dynamics of the tunnel diode can be given by

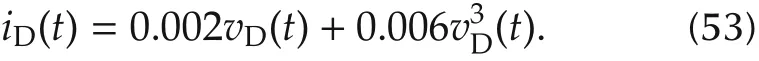
By applying Kirchhoff’s law,the dynamics of the circuit can be obtained,

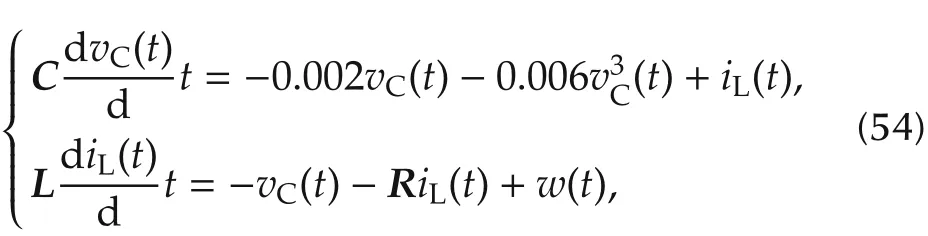
where vC(t),iL(t),and w(t)denote the measured signal,signal to be estimated,and the disturbance input,respectively.In this tunnel diode circuit,it is assumed that|vC(t)|?2 V,and the parameters are selected as follows,R=10Ω,L=1000 mH,and C=20 mF.Selecting x(t)=[vC(t);iL(t)]as the state variables,yields the following nonlinear system:

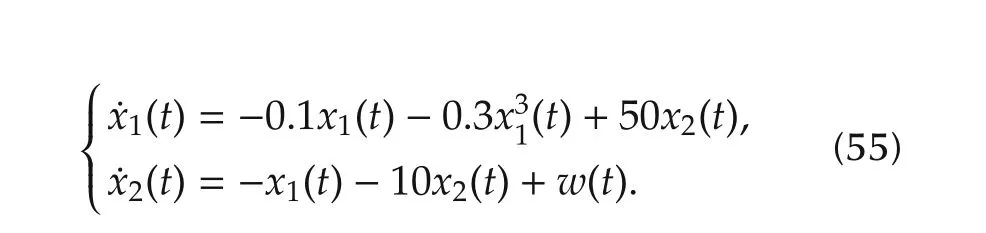
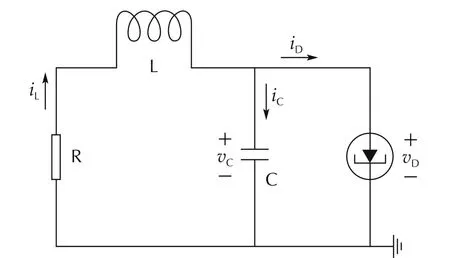
Fig.1 Tunnel diode circuit.

With the aim of using a T-S fuzzy affine model to represent the nonlinear system(55),one can linearize the plant around the points x(t)=(-2;0),x(t)=(0;0),and x(t)=(2;0),and consider the differences between the linearized local model and the original nonlinear plant as norm-bounded uncertainties.Then,one has the T-S fuzzy affine system of the form(1)with local system matrices given by

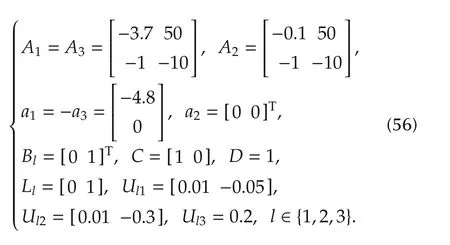
The normalized membership functions are depicted in Fig.2.The following three regions can be obtained,S1:={x∈R2|-2?x1?-0.6},S2:={x∈R2|-0.6?x1?0.6},and S3:={x∈R2|0.6?x1?2}.With the region partition information,the constraint matrices Fi,fi,Qi,and qi,i∈I can be computed in the following forms:

By the regions depicted in Fig.2,one has I={1,2,3},I(1)={1,2},I(2)={2},I(3)={2,3}.Obviously,S2is a crisp region,and S1and S3are fuzzy regions.In this example,it is assumed that the sampling period is h=1 ms andτ=50 ms.

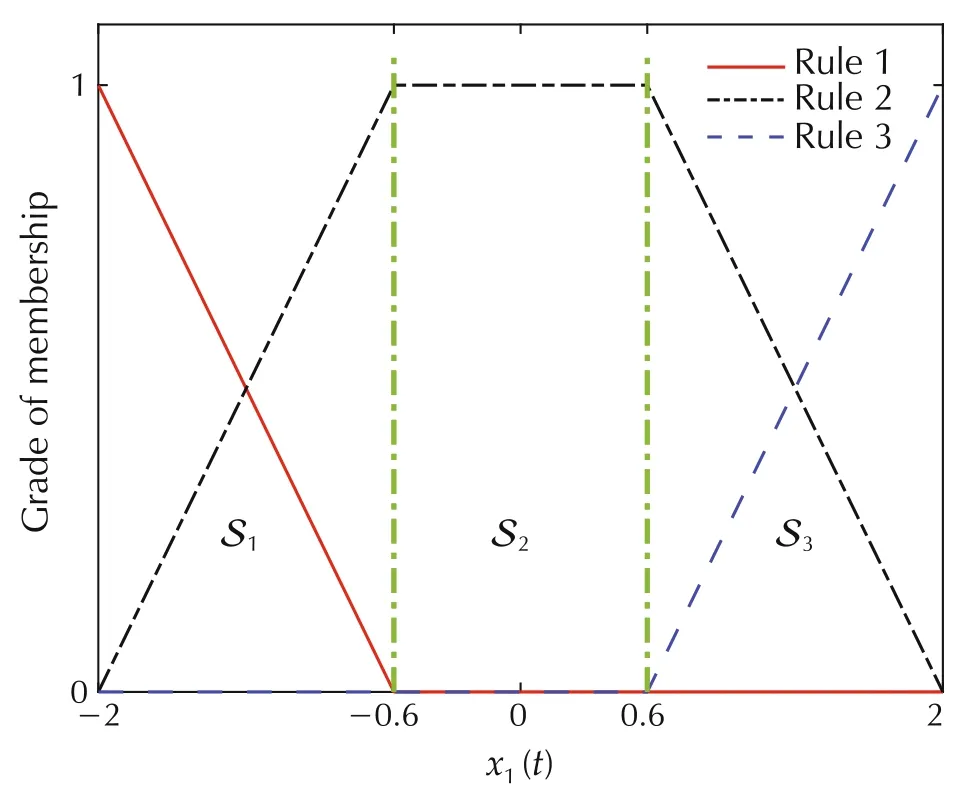
Fig.2 Membership functions.

The purpose is to design an observer(15)for the T-S fuzzy affine system(8)under the event triggered scheme(10)such that the estimation error system(19)is asymptotically stable with H∞performance γ.

Note that by Algorithm 1 with[Fi|fi]=[Inx|0nx×1],i∈ I,the PLKF will reduce to CLKF,thus,the H∞index can be obtained in CLKF-based framwork.First,we will show the less conservative of the PLKF-based observer design approach over the CLKP-based ones.By Algorithm 1 with δ=0.1,0.2,0.3,0.4,and 0.5 the detailed comparison of the minimum H∞performance indices γminbased on PLKF and CLKF are listed in Table 1,respectively.From Table 1,it can be observed the betterperformance ofthe PLKF-based approach overthe CLKF-based ones.

Next,we will show that for given H∞performance index γ applying Algorithm 2 can obtain the maximum event-triggered threshold δmax.By Algorithm 2 with γ=0.5,one indeed obtains feasible solutions with δmax=0.0688 and Φ =0.0402.The corresponding observer gains can be obtained as

Table 1 The H∞performance obtained by different methods.

In the simulation,the disturbance input is selected as

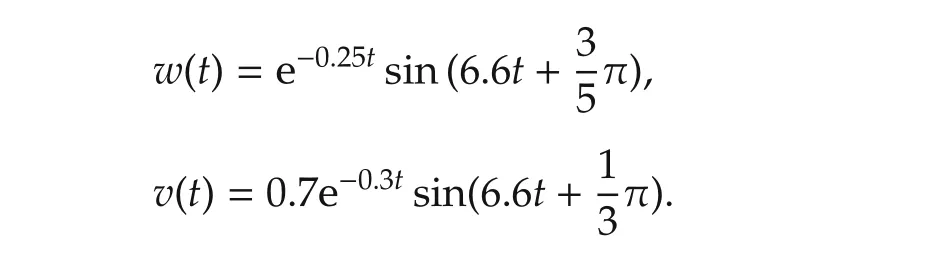
Fig.3 depicts the simulation results of the system and observer states under initial conditionx(0)=[0.4 0.01 0.4 0.01]T.Fig.4 depicts the responses of the ratiounder zero initial condition,from which it is easy to see that the ratio is smaller that the given disturbance attenuation index γ=0.5.Thus,the designed piecewise fuzzy observer can achieve satisfactory performance.

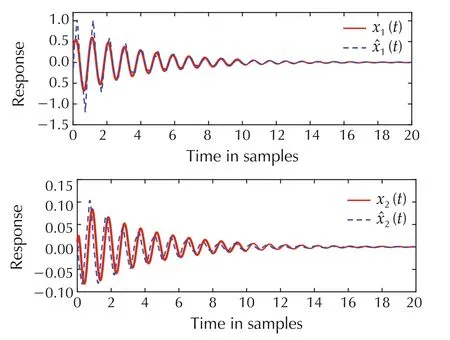
Fig.3 Response of the system and observer states.

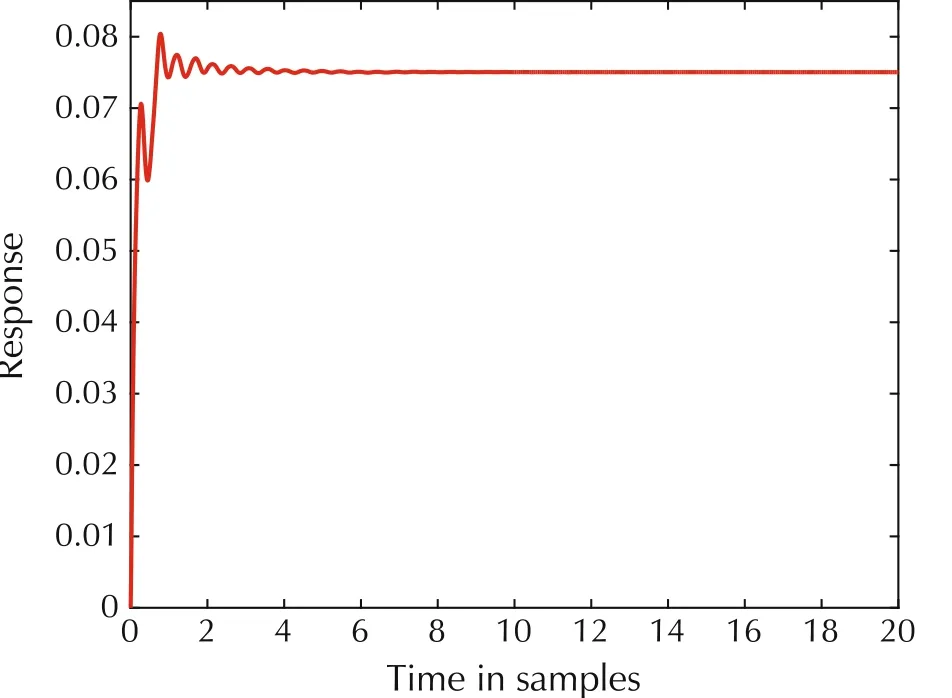
Fig.4 Response of the ratio

5 Conclusions

In this paper,the problem of event-triggered H∞state estimation for T-S fuzzy affine systems is investigated.By adopting the input delay method,the estimation error system can be reformulated as a piecewise delay system.Based on a piecewise Lyapunov-Krasovskiifunctional and the Finsler’s lemma,the event-triggered H∞observer design method is developed.Moreover,an algorithm is proposed to co-design the observer gains and the event-triggering parameters to guarantee that the estimation error system is asymptotically stable with a given disturbance attenuation level and the signal transmission rate is reduced.Finally,simulation studies are given to show the effectiveness of the proposed approach.

Appendix

Lemma A1(Finsler’s lemma)[44]Let x ∈ Rn,P=PT∈Rn×n,and H ∈ Rm×nsuch that rank(H)=r＜ n.The following statements are equivalent:

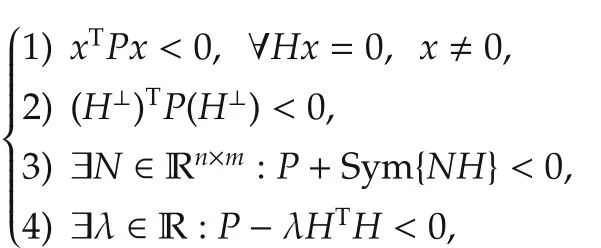
where H⊥denote the right null spaces of H.

Lemma A2[44]Let matrices W=WT,U,V,and Δ(t)be of appropriately dimensional real matrices.The inequality

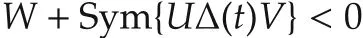
is solvable for all admissible Δ(t)subject to(3),which is equivalent to

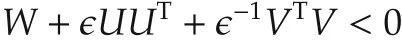
for some positive scalar ϵ.

Meng WANGreceived the B.Eng.degree in Automation from Northeastern University at Qinhuangdao,Qinhuangdao,China,in 2011,and the M.Eng.degree in Control Science and Engineering from the Harbin Institute of Technology,Harbin,China,in 2013.He is currently pursuing the Ph.D.degree in Mechanical and Biomedical Engineering from the City University of Hong Kong,Kowloon,Hong Kong.His research interests include robust control and filtering,fuzzy systems and control,and their engineering applications.E-mail:mwang48-c@my.cityu.edu.hk.

Jianbin QIUreceived the B.Eng.and Ph.D.degrees in Mechanical and Electrical Engineering from the University of Science and Technology of China(USTC),Hefei,China,in 2004 and 2009,respectively.He also received the Ph.D.degree in Mechatronics Engineering from the City University of Hong Kong,Kowloon,Hong Kong in 2009.He has been with the School of Astronautics,Harbin Institute of Technology since 2009,where is currently a Full Professor.His current research interests include intelligent and hybrid control systems,signal processing,and robotics.Prof.Qiu is a Senior Member of IEEE and serves as the chairman of the IEEE Industrial Electronics Society Harbin Chapter,China.He is an Associate Editor of IEEE Transactions on Cybernetics.E-mail:jbqiu@hit.edu.cn.

Gang FENGreceived the Ph.D.degree in Electrical Engineering from the University of Melbourne,Australia.He has been with City University of Hong Kong since 2000 after serving as lecturer/senior lecturer at School of Electrical Engineering,University of New South Wales,Australia,1992-1999.He is now Chair Professor of Mechatronic Engineering.He has been awarded an Alexander von Humboldt Fellowship,the IEEE Transactions on Fuzzy Systems Outstanding Paper Award,and Changjiang chair professorship from Education Ministry of China.He is listed as a SCI highly cited researcher by Clarivate Analytics.His current research interests include multi-agent systems and control,intelligent systems and control,and networked systems and control.Prof.Feng is an IEEE Fellow,an associate editor of Journal of Systems Science and Complexity,and was an associate editor of IEEE Transactions on Automatic Control,IEEE Transactions on Fuzzy Systems,IEEE Transactions on Systems,Man&Cybernetics-Part C,Mechatronics,and Journal of Control Theory and Applications.E-mail:megfeng@cityu.edu.hk.