Distributed optimal consensus of multiple double integrators under bounded velocity and acceleration

Zhirong QIU ,Lihua XIE †,Yiguang HONG

1.School of Electrical and Electronic Engineering,Nanyang Technological University,Singapore 639798;

2.Key Laboratory of Systems and Control,Institute of Systems Science,Chinese Academy of Sciences,Beijing 100190,China

Received 24 August 2018;revised 2 October 2018;accepted 9 October 2018

Abstract This paper studies a distributed optimal consensus problem for multiple double integrators under bounded velocity and acceleration.Assigned with an individual and private convex cost which is dependent on the position,each agent needs to achieve consensus at the optimum of the aggregate cost under bounded velocity and acceleration.Based on relative positions and velocities to neighbor agents,we design a distributed control law by including the integration feedback of position and velocity errors.By employing quadratic Lyapunov functions,we solve the optimal consensus problem of double-integrators when the fixed topology is strongly connected and weight-balanced.Furthermore,if an initial estimate of the optimum can be known,then control gains can be properly selected to achieve an exponentially fast convergence under bounded velocity and acceleration.The result still holds when the relative velocity is not available,and we also discuss an extension for heterogeneous Euler-Lagrange systems by inverse dynamics control.A numeric example is provided to illustrate the result.

Keywords:Distributed optimization,double integrators,bounded velocity,bounded input

1 Introduction

Fora multi-agentsystem,the optimalconsensusproblem aims to achieve the consensus among different agents,where the final consensus value is required to minimize a global cost.Usually,the global cost is given by the sum of individual costs,which are often assumed to be convex.Specifically,this problem is closely related with the distributed optimization problem arising from parallel and distributed computing,which focuses on discrete-time iteration algorithms without considering the agent dynamics.A variety of optimization algorithms have been designed in a distributed manner[1-4],and have found applications in big data[5]and distributed learning[6].It is also intriguing and promising to implement these algorithms to practical systems such as robots and unmanned vehicles,in an effort to improve the performance of collective tasks.

To this aim,the corresponding continuous-time system dynamics and the constraints on the state and the input need to be considered.There have been many results considering the optimal consensus problem for continuous-time systems,with first-order integrators receiving the most attention.Based on dual decomposition,Wang and Elia proposed a saddle-point algorithm to solve an unconstrained optimization problem in[7].The algorithm was further refined in[8]and[9]by treating the dual variable as an integral feedback to correct the consensus error,thus avoiding the communication of dual variables.The case with a common set constraint wasconsidered in[10]by adapting the projected subgradient algorithm,and the case of different set constraints was investigated in[11].S.Yang et al.[12]proposed a proportional-integral protocol to solve the problem.D.Mateos-Nez and J.Corts[13]dealt with coupling inequality constraints by using saddle-point dynamics with averaging of primal and dual variables.P.Yi et al.[14]investigated the case with different set constraints and coupling equality constraints for resource allocation problems.Higher-order system dynamics are also considered,e.g.,the Euler-Lagrange(EL)systems[15,16]and high-order integrators[17].On the other hand,although the bounded control problem is very important in practice,it is not duly explored,except the recent work[18]which considered the first and second order integrators.More relevant works can be found in the multi-agent consensus literature and different approaches have been proposed,e.g.,by using a low gain feedback approach[19,20],or by tracking a virtual system with bounded control for double integrators and EL systems[21,22],or by using a nested saturated function[23,24].

In this paper,we study the distributed optimal consensus problem for multiple double integrators under bounded velocity and acceleration.Each agent is assigned with an individual cost,which is strongly convex and assumes Lipschitz continuous gradients.To achieve consensus at the optimum of the aggregate cost,a distributed control protocol is designed for each agent by including the following terms:a weighted sum ofrelative positions to its neighbors,a damping term of its velocity,a gradient descent of its individual cost,as well as an integral feedback of the relative position and the relative velocity.With the aid of quadratic Lyapunov functions,we show that the designed control law leads to an exponentially fast convergence to the global optimum under a strongly connected and weight-balanced network.If an initial estimate of the optimum is known,then the control gains can be further refined so that the optimal consensus is achieved under bounded velocity and acceleration.By using inverse dynamics control,the above result can be extended to heterogeneous EL systems with bounded velocity and control input,if the nonlinearity of each system is exactly known.Comparing with previous works,two major contributions are summarized as follows.On one hand,we not only extend the exponential convergence result in[15]for a wider class of networks which are strongly connected and weight balanced,but also achieve a similar result when the relative velocity is not available.On the other hand,an exponentially fast optimal consensus is achieved under bounded velocity and acceleration,while[18]only achieved the convergence under bounded acceleration.Although a priori knowledge of the optimum is needed to properly tune the control gains,positive definite Hessians are notrequired forindividualcosts,which is more general than the case studied in[18].

The rest of this paper is organized as follows.After briefly reviewing some preliminaries about graph theory and convex functions in Section 2,we formulate the problem under investigation in Section 3.Then we establish the optimal consensus for double-integrator multi-agent systems in Section 4.1,and extend the result to the case of EL dynamics in Section 4.2.A numeric example is provided in Section 5 to illustrate the result,and the whole work is concluded in Section 6.

Notations R and R?0respectively denote the real and nonnegative real numbers.A vector x is always viewed as a column vector,and 1 is a vector of ones with a compatible dimension.〈x,y〉is the standard inner product for vectors x and y,while ‖x‖and ‖x‖∞are respectively the 2-norm and infinity norm of x.diag{a1,...,an}denotes a diagonal matrix with diagonal entries given by a1,...,an.col{x1,...,xn}=[x′1,...,x′n]′.For a symmetric matrix A ∈ Rn×n,λmin(A)and λmax(A)respectively denote its smallest and largest eigenvalues.denotes a summation for all possible indexes i,which similarly applies to

2 Preliminaries

2.1 Graph theory

The communication between different agents within a multi-agent system can be modeled as a digraph G,which consists of a node set N={1,...,N}and an edge set ℰ ={(i,j):i,j∈ N}excluding self-loop(i,i).(i,j)∈ℰ indicates that node j can receive information from node i,and N+i={j:j∈ N,(j,i)∈ ℰ}andrespectively denote the inand out-neighbor sets of node i.G is said to be strongly connected if there always exists a path between two different nodes i and j,which is given as an ordered edge sequence(i,n1),...,(nk,j).A non-negative matrixcan be assigned as the weights on the edges,with aij＞ 0 iff(j,i)∈ ℰ.The triplet{N,ℰ,A}completely definesa weighted digraph G.If A=A′,then G is said to be undirected,in which case it is also said to be a connected graph if it is strongly connected.The weighted in-and out-degrees of node i are respectively given byeach i,then G is weight-balanced.The Laplacian matrix L can be used to examine the connectivity of G,which is defined by L=DG-A with D+G=diag{D+1,...,D+N}.Note that L1=0,and G is strongly connected iff zero is a simple eigenvalue.For an undirected graph,it is connected iff the N eigenvalues of L can be rearranged as 0= λ1＜ λ2?...? λN.If G is weight-balanced,thenis also a Laplacian matrix.Therefore,for a weight-balanced graph,it is strongly connected iff the N eigenvalues ofcan be rearranged as 0=λ1＜λ2?...?λN.

2.2 Convex functions

A function f:Rm→R is convex if the inequality

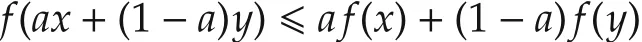
holds forany x,y and 0?a?1.If f is differentiable with gradient∇f,then we have f(y)-f(x)? 〈∇f(x),y-x〉.Given a positive constant ω,f is called ω-strongly convex if

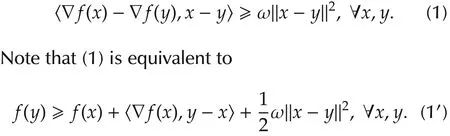
3 Problem formulation

Consider N agents with the following doubleintegrator dynamics:

where pi,vi,ui∈Rmrespectively denote the position,velocity and acceleration vectors.Each agent i is assigned with an individual cost fi,and we aim to design a distributed control law for all agents to cooperatively minimize the aggregate cost:

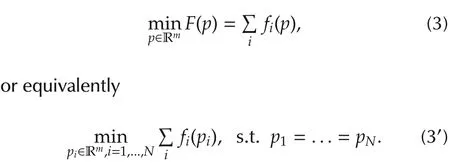
In this paper,we are concerned with those cost functions which satisfy the following assumption.

Assumption 1 For each i,fiis differentiable and ωstrongly convex,and ∇ fiis θ-Lipschitz,namely

As a result of the strong convexity,the optimum of(3)is unique,and we denote it as p＊.Accordingly,the optimal consensus problem is equivalent to that

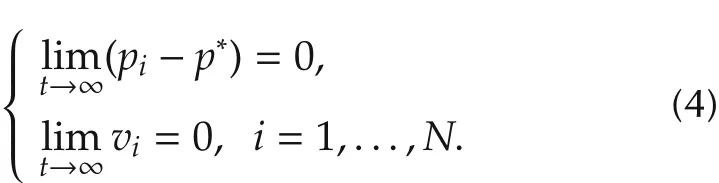
By the optimality condition of differential functions,we

Furthermore,in practical implementation the velocity viand acceleration uiare required to be bounded,respectively for safety reason and actuator limitation.Without loss of generality we consider a symmetric bound for each component as follows:

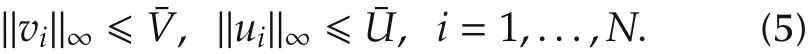
To design the control gains,we also need to know some a priori knowledge about the initial position and velocity,as stated in the following assumption.

Assumption 2 Foreach agent i,there exists a known constant R such that the optimum p＊is initially within the range of R,i.e., ‖p＊-pi(0)‖?R,and the initial velocity is bounded by‖vi(0)‖∞?v0?V.

4 Main results

In this section we are to study the optimal consensus(4)of multiple double integrators under constraints(5).After establishing the exponentially fastoptimalconsensus result for double integrators in Section 4.1,we further discuss an extension to the case of EL dynamics by employing inverse dynamics control in Section 4.2.See the following two subsections for details.

4.1 Optimal consensus of double integrators

To solve the optimal consensus problem for agents with double-integrator dynamics(2),we design the control input uifor each agent as follows:

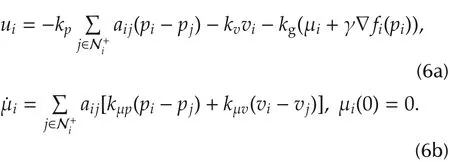
Note that the control input has a similar from as in[15],which consists of the following four terms:a weighted sum of position differences from its neighbors,a damping term of its velocity,a gradient descent of its individual cost for local minimization,as well as an integral feedback μiof the relative position and the relative velocity to correct the gradient differences.With different control gains for different terms,we are able to address the bounded velocity and acceleration which were not considered in[15],as well as the case when the relative velocity is not available.

Below we show that the optimal consensus problem(4)under constraint(5)can be solved with a proper selection of control gains,if the network is strongly connected and weight-balanced.Denoteλ2andλNrespectively as the smallest and largest positive eigenvalues of L.To choose the control gains,let kv＞0,c12∈(0,kv),and c23＞ 0.If the relative velocity is available(kμv＞ 0),take kp,kμp,and kμvas

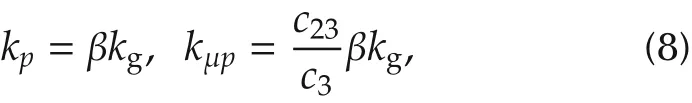
Theorem 1 Let G be strongly connected and weightbalanced.Under Assumption 1 and the controller(6)with control gains given by(7)or(8),we can always find proper kgand γ such that

1)The optimal consensus(4)is achieved at an exponential convergence rate.If the relative velocity is available,then kgand γ need to respectively satisfy the following inequalities with ζ2=kv-c12:

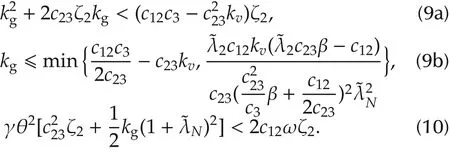
If the relative velocity is not available,then γ needs to satisfy(10),and kgneeds to satisfy(9a)and the following inequality

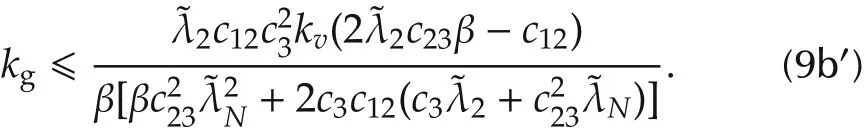
2)If Assumption 2 is satisfied,then the exponentially fast optimal consensus(4)can be achieved under constraints(5).Specifically,select kvby

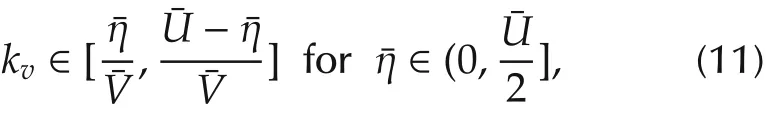
and let kgfurther satisfy that

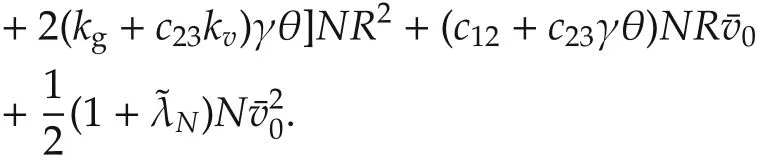
Remark 1 Comparing with[15]which achieved an exponentially fast optimal consensus for multiple double-integrators for undirected and connected networks,we consider a wider class of networks as being strongly connected and weight-balanced,as well as the case when the relative velocity is not available.On the other hand,an exponentially fast optimal consensus is achieved under bounded velocity and acceleration,while[18]only achieved the convergence under bounded acceleration.Although a priori knowledge of the optimum is needed to properly tune the control gains,positive definite Hessians are not required for individual costs,which is more general than the case studied in[18].

Remark 2 It is readily seen that the selection of the velocity damping gain kvis to satisfy the velocity constraint,which is only dependent on the constraints and independent from other gains.γ is the gradient gain which determines the size of individual gradient descent.Moreover,by(7)we know that c3,c23and β respectively tune the ratios between the control gains kμv,kμp,kpand kg.Specifically,the set of inequalities(9)always admits positive solution of kgas long as,and c12∈(0,kv).Once kghas been fixed,then γ can be found by(10)for any fixed kg＞0.It is also worth mentioning that although the upper bound of initial velocitiesv0?V does not need to be known to solve kg,a more accurate estimate ofv0enables a richer choice of kg,as implied from(29)and the definition ofV0.For instance,if each agent starts from a static state,thenIn comparison with the design process in[25]which depends on finding sufficiently small gains,the result in this paper not only provides a more flexible choice of control gains with less computation,but can also be applied to nonzero initial velocities,which is more suitable for practical implementation.

Proof of Theorem 1 The proof is divided into 3 parts as follows.In the first place we introduce some notations and rewrite the closed-loop system around the equilibrium,then we constructa quadratic Lyapunov function candidate to show the exponentialconvergence respectively for the cases of kμv＞ 0 and kμv=0.Finally,we choose proper gains to satisfy the constraints(5).In the following,we let m=1 since the same analysis can be applied to each component.

1)(Disagreement dynamics)Denote

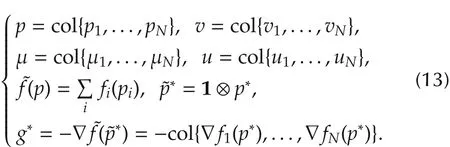
Furthermore,letρ=p-p＊andδ=μ-γg＊,and combine(2)and(6)into a closed-loop system as

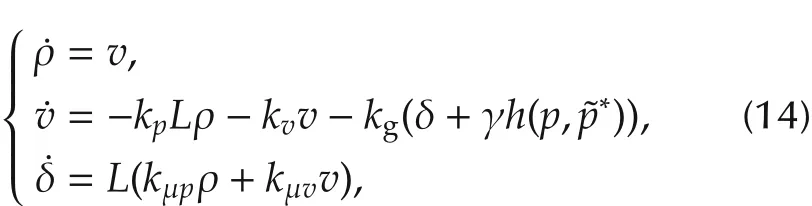
where L is the Laplacian matrix of G,and h(p,p＊)=Below h(p,p＊)will be abbreviated as h.Noticing that G is strongly connected and weightbalanced,we can find an orthogonal matrix W=[wsuch that W′LW=diag{0}withI withbeing respectively the smallest and largest positive eigenvalues ofL.By applying the following state transformationsρ=col{ρ1,ρ2:N}=W′ρ,v=col{v1,v2:N}=W′v andδ=col{δ1,δ2:N}=W′δ to system(14)with ρ1,v1,δ1∈Rm,we obtain that

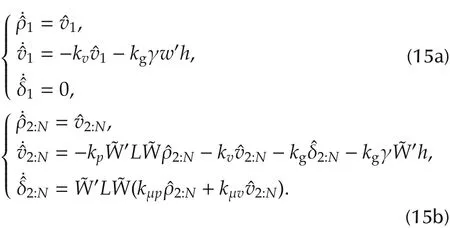
Note that(15a)holds as a consequence of w′δ =,since we havethe equilibrium p＊,and 1′Nμ ≡ 0 by observing that0 from(14)together with the initial condition

2)(Quadratic Lyapunov function and exponentialconvergence) We first consider the case of kμv＞ 0.To prove the the convergence to the optimum,we define a quadratic Lyapunov function candidate as

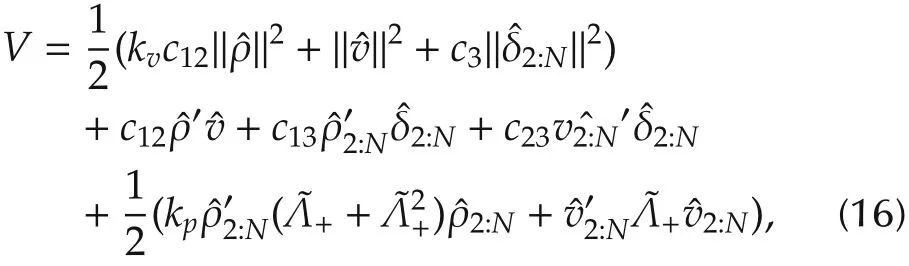
where c13=kg+c23kv.Clearly,it suffices to ensure the positive definiteness of V ifis positive definite,which is equivalent to that 0＜c12＜kvandReplacing c13=kg+c23kvandζ2=kv-c12,the lattercondition is exactly(9a).Noticing that x′W′LW y=x′Λ+y for any vectors x and y,˙V can be calculated by(15)as

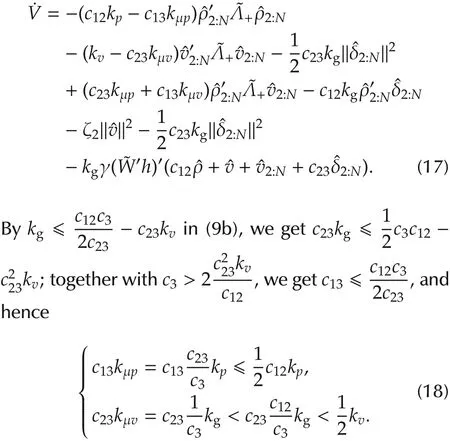
By combining(18)and Assumption 1 into(17),we can estimate the upper bound of˙V as

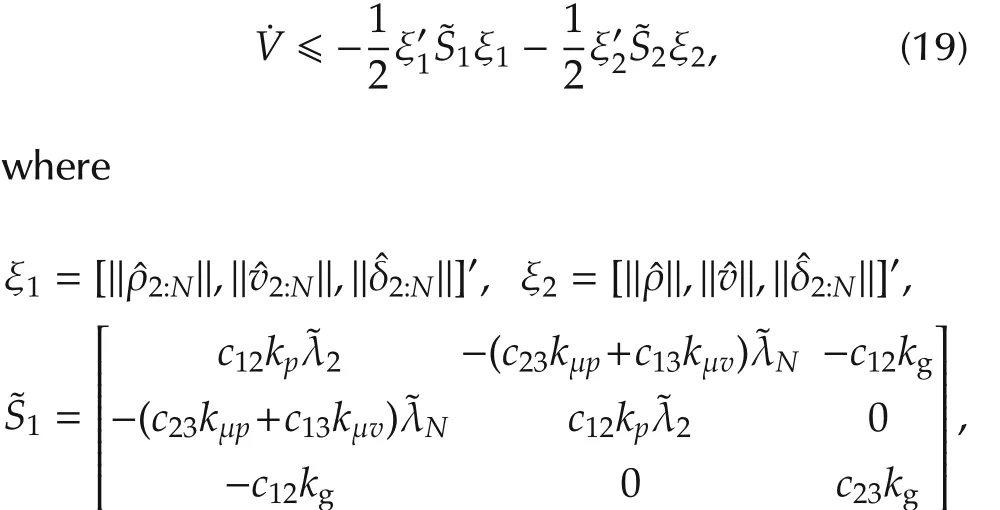
To show that V˙ is negative definite,it is enough to show that S1is positive semi-definite and S2is positive definite,which is equivalent to that det S1?0 and det S2＞0 by direct computation.To be detailed,

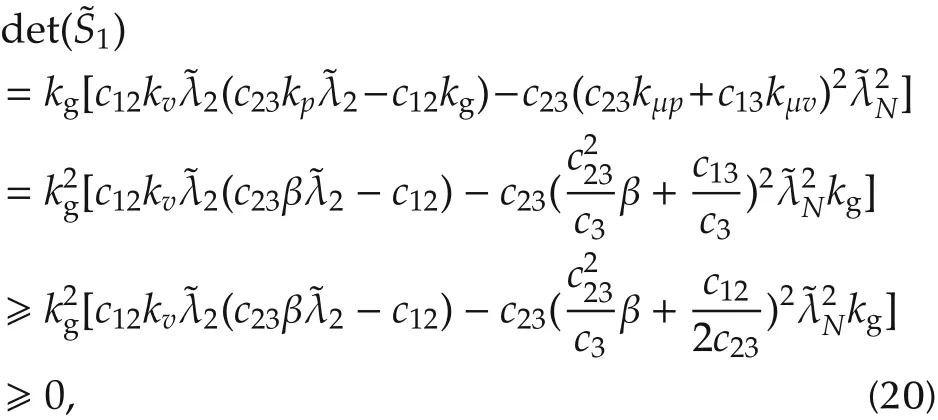
When kμv=0,we can proceed along the same line as in the above to obtaina similar estimate to(19),where S1

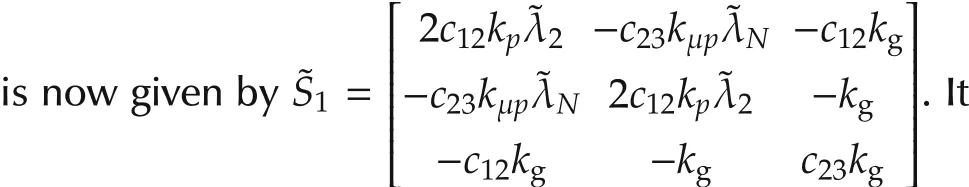
can be easily checked thatthe positive semi-definiteness ofis guaranteed by(9b′)with β ＞over,since,(18)holds naturally without the,and it suffices to requireso that(9a)admits positive solutions of kg.Therefore,the exponential convergence can be preserved if the other conditions remain the same.

3)(Optimalconsensusunderconstraint(5))We first discuss the bounded velocity requirement.Recall that we have assumed that viis a scalar,whose dynamics is given by(14)as v˙i=-kvvi+ηi,with ηibeing the i th entry of η=-kpLρ-kg(δ+γh).Assume that|ηi|?η,then it is easy to show that

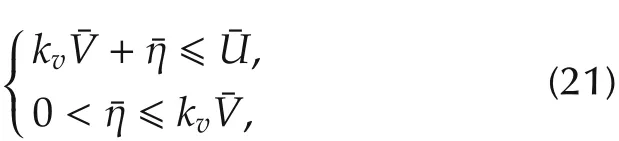
which is equivalent to(11).Based on the above discussion,next we shall estimate ‖η‖∞.

To be detailed,note that the upper bound of η is dependent on that of ρ and δ,which can be estimated by employing the quadratic Lyapunov function in step 2).Actually,˙V(t)?0 implies that

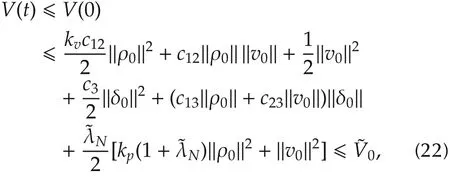
whereV0is defined in(12),and the subscript 0 denotes the corresponding initial values of ρ,v,and δ,and we used the facts that‖δ0‖= ‖μ0-γg＊‖= ‖γg＊‖? γθ‖ρ0‖,‖v0‖2?Nv20and‖ρ0‖2?N R2.To find an upper bound for ρ and δ,note that

Therefore,to guarantee an exponentially fast consensus(4)under the constraint(5),it suffices to further require kvand kgrespectively satisfy(11)and(12).

If the network is undirected and connected,then we can find simpler conditions to select the control gains by employing a simpler Lyapunov function.In this case,given kv,γ＞0,c12∈(0,kv),and b23,c3＞0,select kp,kμp,and kμvas

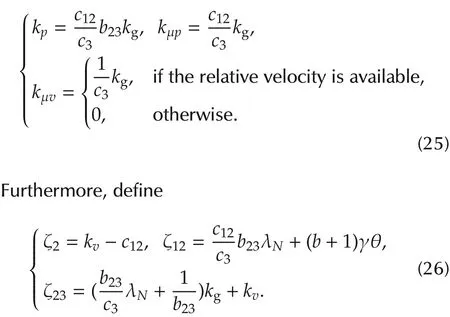
Then an exponentially fast optimal consensus can be achieved by properly choosing kgas follows.

Theorem 2 Let G be undirected and connected,and denoteλ2andλNrespectively asthe smallestand largest positive eigenvalues of L.Under Assumption 1 and the controller(6)with control gains given by(25),we can always find proper γ such that

1)The optimal consensus(4)is achieved at an exponential convergence rate.

If the relative velocity is available,then kgneeds to satisfy the following inequalities for a proper selected b＞0:

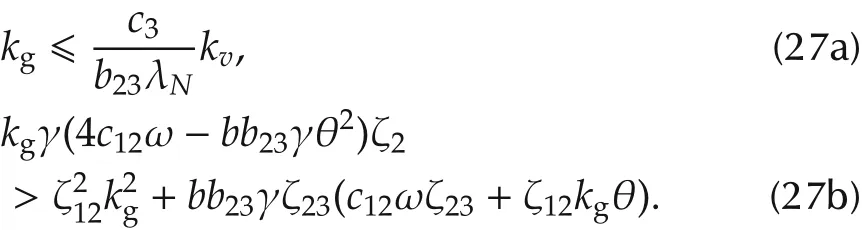
If the relative velocity is not available,then kgneeds to satisfy the following inequalities:

2)If Assumption 2 is satisfied,then the exponentially fast optimal consensus(4)can be achieved under constraints(5).Specifically,select kvby(11),and let kgfurther satisfy that

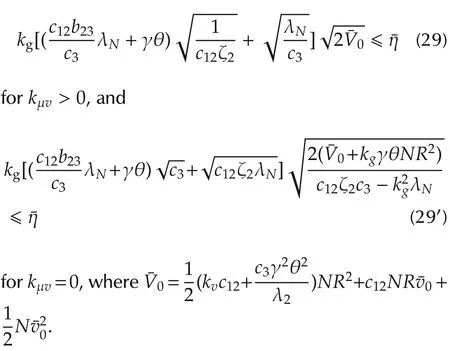
Remark 3 In comparison with Theorem 1,it can be seen that there is less restriction in choosing the control gains.Actually,the ratios between the control gains kμv,kpand kgwhich are determined respectively by c3and b23,can now be chosen arbitrarily.This is also the case for the gradient gain γ,and we only need to solve the inequalities with respect to kg.With a properly selected b,positive kgcan always be found to satisfy(27b)or(28b),since either one can be approximated by the following inequality with sufficiently small b＞0:

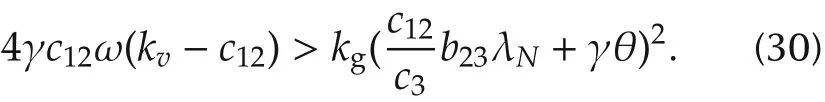
Furthermore,itis worthwhile mentioning thatby using a Lyapunov function with negative semi-definite derivative as shown in the subsequent proof,the required condition(29)to satisfy the bounded acceleration for kμv＞ 0 is much simpler than the corresponding condition(12)in Theorem 1.

Remark 4 When the relative velocity is available,i.e.,kμv＞ 0,we may select kgto accelerate the convergence when the other parameters haven been decided.Actually,in the proof we employ a quadratic Lyapunov function V to show the exponential convergencewhere S is defined in(34)andIn this case,given an er-ror bound ϵ,an upper bound of the time T for all agents reaching the ϵ-neighbor hood of the optimum is foundHence,a faster convergence can be expected with a larger α.Since kgonly appears in S which is linearly dependent on kg,we can find the optimal kgby solving the following semidefinite programing problem:

To obtain a larger α,the other parameters can be determined by a grid search[26].Still,it should be pointed out that the design of control gains depends on the specific choice of V,and the corresponding α only provides a lower bound of the convergence rate,which may be conservative.

Proof of Theorem 2 The proof follows a similar line to the proof of Theorem 1,by using different Lyapunov functions for different cases.Noticing that G is undireted and connected,we can always find an orthogonal matrixsuch that W′LW=diag{0,λ2,...,λN}with 0 ＜ λ2?...? λN.By multiplying W′to ρ,v and δ respectively,we can similarly obtain the transformed disagreement dynamics as(15),withW′LW in(15b)replaced by Λ+=diag{λ2,...,λN}.Below we discuss the cases of kμv＞ 0 and kμv=0 respectively.

1)kμv＞ 0.To prove the convergence to the optimum,we define a quadratic Lyapunov function candidate as

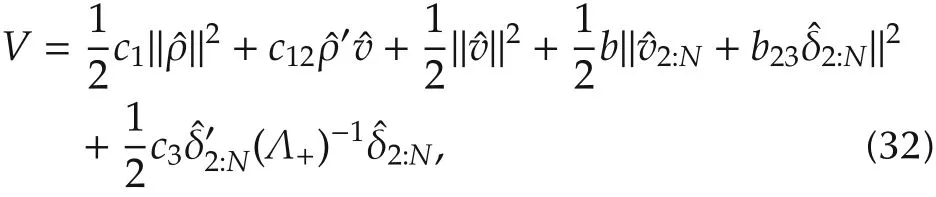
where we let c1=c12kv.Similar to(19),we can find an upper bound of˙V as

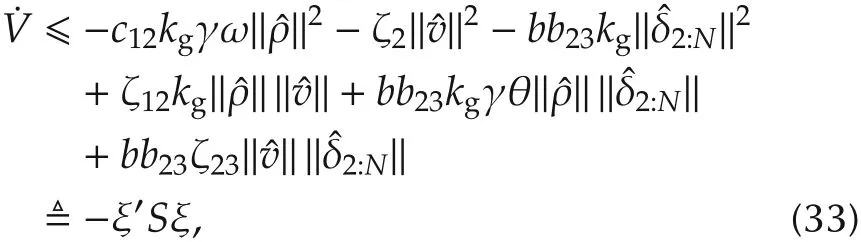
where ζ2,ζ12,ζ23have been defined in(26),ξ=[‖ρ‖,‖v‖,‖δ2:N‖]′,and S=[sij]∈R3×3is a symmetric matrix whose entries are given by

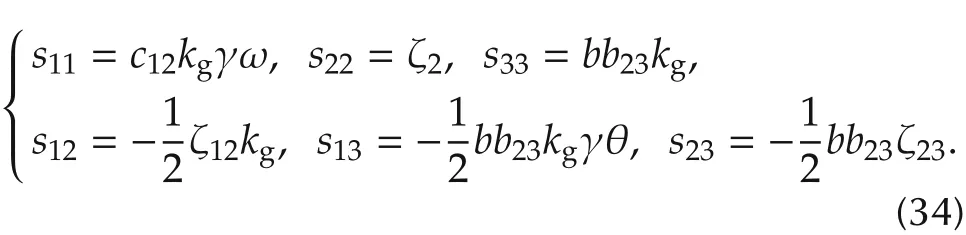
Obviously,to ensure the positive definiteness of V,it suffices to letwhich is equivalent to

Furthermore,to ensure the negative definiteness of˙V,it suffices to require that S be positive definite,which is equivalent to Sk＞0 with Skbeing the k th leading principal minor of S for k=1,2,3.Direct computation shows that S1=s11,S2=s11s22-and

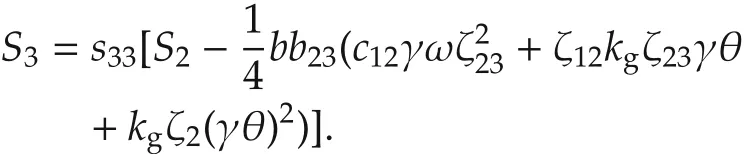
Therefore,with ζ2＞0,the negative definiteness of˙V is equivalent to S3＞0,which is ensured by(27b).

To satisfy the velocity constraint,the same argument in the proof of Theorem 1 can be applied.On the other hand,to meet the acceleration bound,we need to estimate the upper bound of η =-kpLρ-kg(δ+γh).In this case,we will use a different Lyapunov function by letting V=V1with b=0.It can be checked that V1is positive defintie with the condition(35),and it can be obtained from(33)that˙V1?-c12kgγω‖ρ‖2-ζ2‖v‖2+(kpλN+kgγθ)ζ12‖ρ‖‖v‖.Therefore,˙V1?0 ifthe condition(27b)holds,which follows that

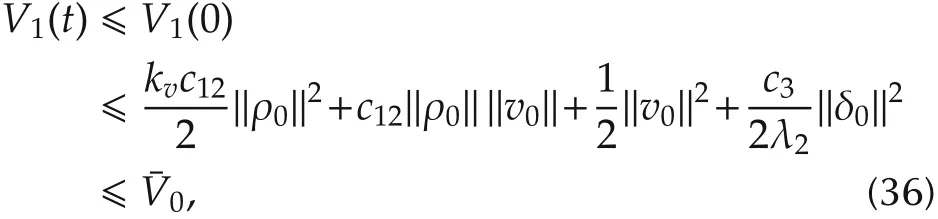
whereV0is defined in(29),and the subscript 0 denotes the corresponding initial values of ρ,v,and δ,and we used the facts that‖δ0‖= ‖μ0-γg＊‖= ‖γg＊‖? γθ‖ρ0‖,

‖v0‖2?Nv20and‖ρ0‖2?N R2.In addition,it can be seen that

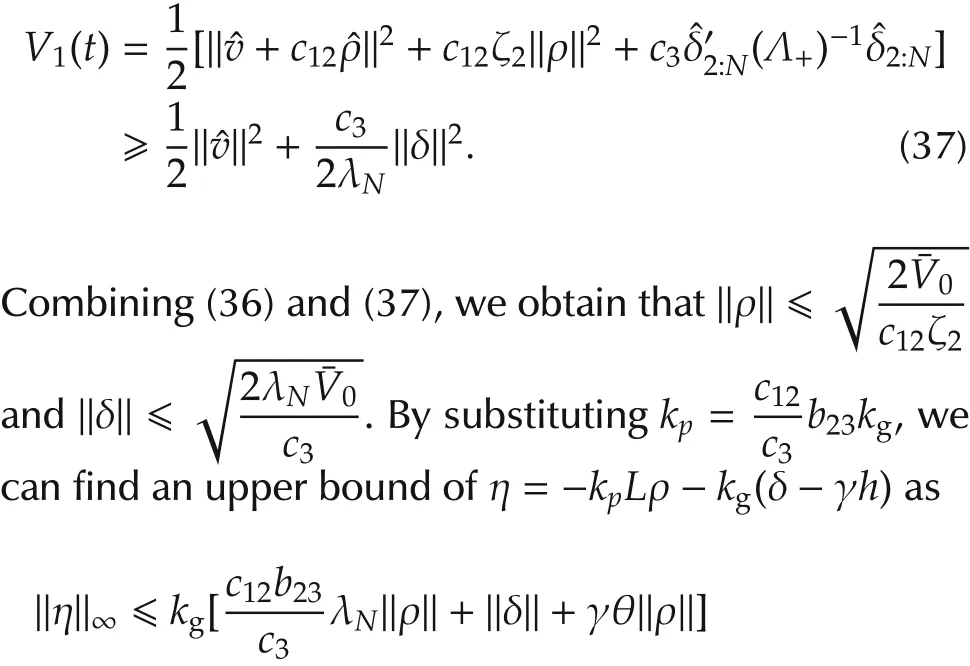
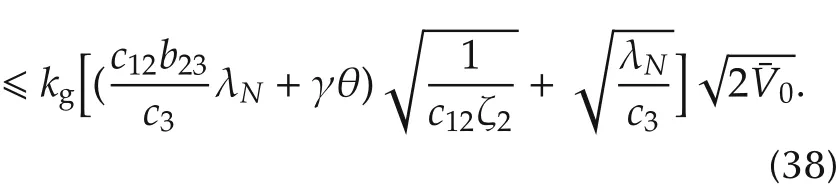
Therefore,to guarantee an exponentially fast consensus(4)under the constraint(5),we can first select η∈(0,U/2]and kv∈[η/V,(U-η)/V],then for fixed γ,b23,c12∈ (0,kv),c3,obtain kgby solving the inequalities(27)and(29)with a properly selected b.The other control gains now can be found by(25).

2)kμv=0.In this case,we revise the Lyapunov candidate(32)by adding an extra termto V,namely V=V+t is easy to verify that the positive definiteness of V is satisfied with

which follows as a consequence of(28a).Moreover,if kg?b23,then by proceeding as(33)we getwhere=[sij]is a symmetric matrix withsij=sij,.Accordingly,the condition(27b)to guarantee the exponentially fast optimal consensus is revised as(28b).Now we have V(t)?V0+kgγθN R2and that

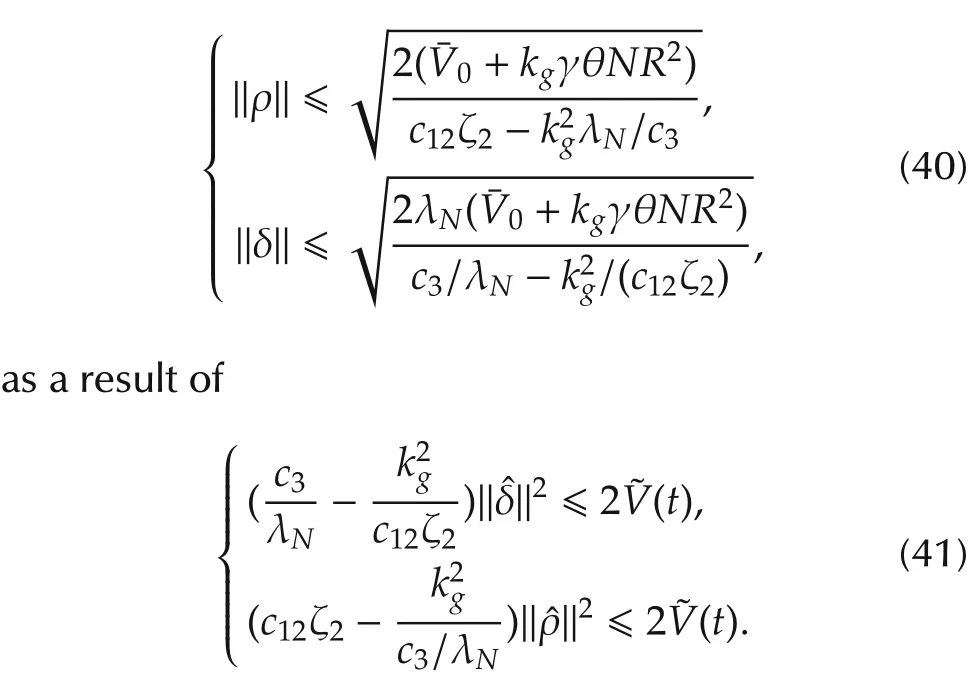
Therefore,in order to achieve the optimal consensus under bounded input,it suffices to revise the corresponding condition as(29′).

4.2 Optimal consensus with EL dynamics

In this section,we shall study the optimal consensus problem for heterogeneous EL systems under bounded velocity and control input.Specifically,consider N agents with the following EL dynamics:

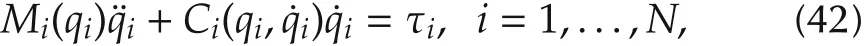
Assumption 3 There exist positive constants M and C such that‖Mi(qi)‖?M and‖Ci(qi,˙qi)‖?C‖˙qi‖.

As the case of double integrators,we assign each agent i with a cost function fiwhich is dependent on the generalized position qi,and aim to achieve the consensus at the minimum of the aggregate cost.Under Assumption 1 we denote the unique optimumand the corresponding optimal consensus problem is given by

Moreover,we are concerned with the following constraints on the generalized velocity and control input:

A similar assumption about the initial state is made below.

Assumption 4 Foreach agent i,there exists a known constant R such thatthe optimum q＊isinitially within the range of R,i.e.,‖q＊-qi(0)‖?R,and the initial velocity is bounded by‖˙qi(0)‖∞?v0?V.

Assuming that Miand Cican be accurately obtained,we are ready to solve the optimal consensus problem(4′)for EL dynamical systems under constraints(5′)by adopting inverse dynamics control.Let τibe given by

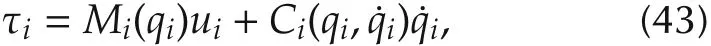
then the originalEL system(42)is reduced to the doubleintegrator system(2).Clearly,if we design uiby

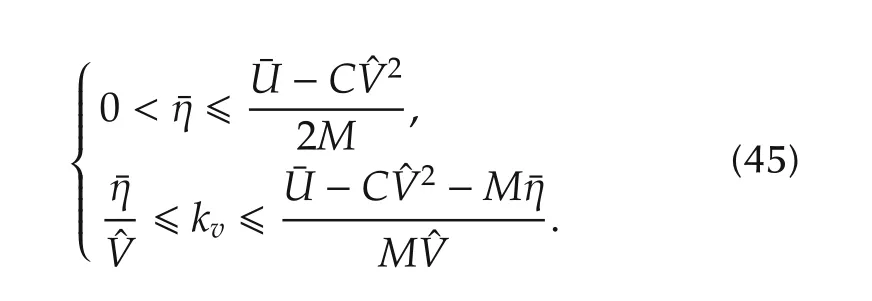
Moreover,ηican be upper bounded similarly as in Theorem 1 or 2,if the initial range of optimum is known,and the initial velocity is bounded by‖˙qi(0)‖∞?V.Consequently,the optimal consensus(4′)can be achieved under the constraint(5′).We summarize the above discussion in the following theorem.

Theorem 3 Let Assumptions 1 and 3 hold,and the controller be given by(43)and(44).Furthermore,let Assumption 4 hold withChoose kvby(45),then for both cases of kμv＞ 0 and kμv=0,the exponentially fast optimal consensus(4′)can be achieved under constraints(5′)by properly selecting the other control gains as follows.

1)If G is strongly connected and weight-balanced,then select the control gains as in Theorem 1.

2)If G is undirected and connected,then select the control gains as in Theorem 2.

Remark 5 Comparing Theorem 3 with Theorem 1 or 2,we find that the only difference is the inequality(45)about kvandη due to the different control τi,which requires a possibly lower bound of velocityV?V due to the additional term Ci˙qi.However,once kvandη have been determined,the other control gains can be found similarly as in Theorem 1 or 2.

5 Numerical example

We consider a 4-agent system with double-integrator dynamics(2)under a connected network.The constraints in(5)are given byV=U=5,respectively corresponding to the maximum velocity and acceleration of 5 m/s and 5 m/s2.Assume that the 4 agents are connected as a circle with weight 0.1 on each edge,which follows that λ2=0.2 and λN=0.4.Furthermore,denote the position of the i th agent as pi=[xi,yi]′,with the corresponding individual cost fi=ai(xi-xi(0))2+bi(yi-yi(0))2,where the coefficients are respectively given by ai=0.3,0.6,0.9,0.6,bi=0.6,0.6,0.3,0.3,and[xi(0),yi(0)]′is the initial position.Let the agents respectively start from[0,0]′,[2,-1]′,[3,3]′and[1,4]′with the initialvelocity given by[-1,0]′,[0.5,2]′,[1,1]′and[0,1.5]′,then it can be inferred that R=5.39 andv0=2.In light of(1′)we can also getshow the efficacy of the control protocol(6),in the following we shall select the control gains as Remark 4,and discuss the influence of the gradient gain γ on the convergence rate and trajectory.

To be detailed,we fix kv=0.5 forη=2.5,c3=c12=and respectively select γ=0.1,0.4 and 0.8.A grid search of b is conducted in[0.01,1]with an increment of 0.01 in each loop,and kgis found by solving the problem(31)in Remark 4.As demonstrated in Figs.1-3,in all cases the consensus can be achieved exponentially fast at the optimum[1.88,0.71]′under bounded velocity and acceleration.Furthermore,it also shows a trade-off between convergence rate and trajectory oscillation:a large γ leads to a smooth trajectory with slow convergence,while a small γ leads to fast convergence with an oscillating trajectory.

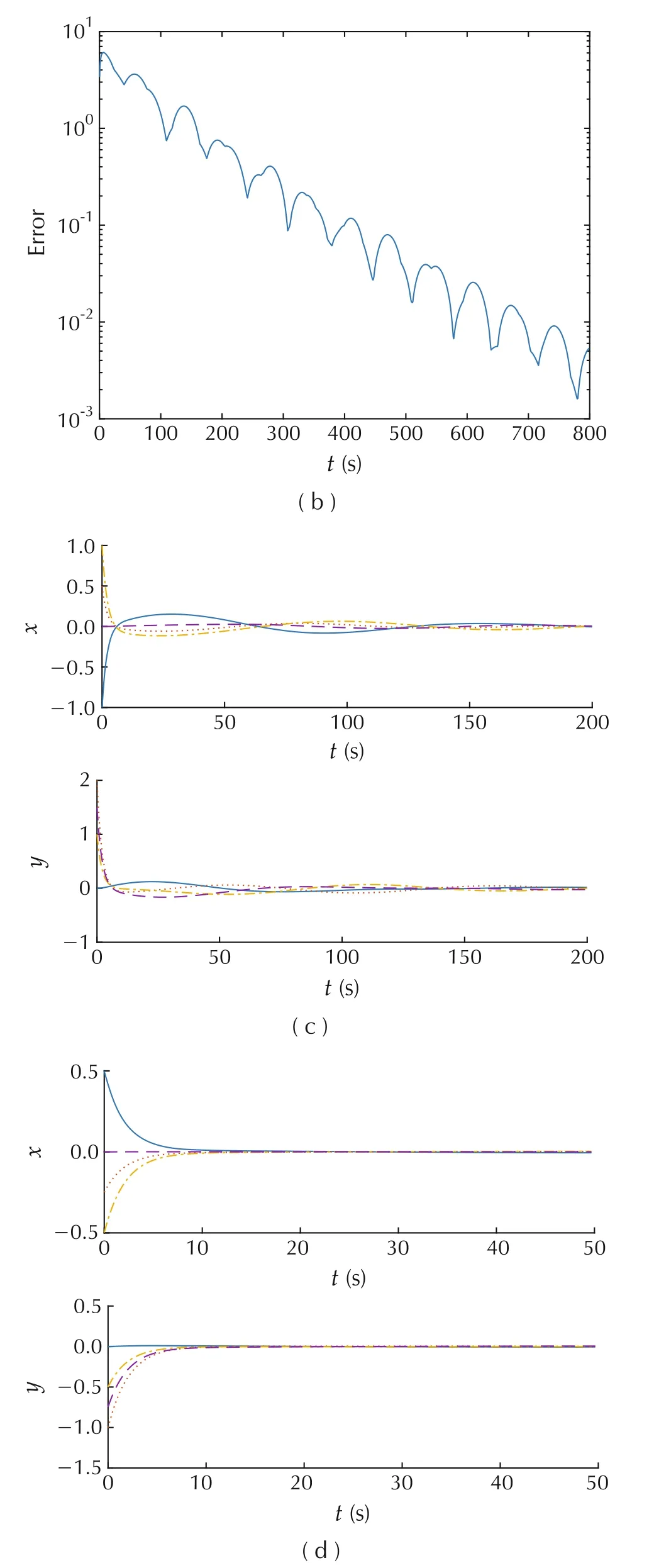
Fig.1 γ =0.1:kv=0.5,k g=kμp=0.0747,kp=0.00747,kμv=0.2986.(a)Plane trajectories.(b)Maximum distance error.(c)Velocity evolution.(d)Acceleration evolution.

Fig.2 γ =0.1:kv=0.5,k g=kμp=0.0269,kp=0.00269,kμv=0.1076.(a)Plane trajectories.(b)Maximum distance error.(c)Velocity evolution.(d)Acceleration evolution.

Intuitively,on the premise of exponential convergence,a larger γ assigns more weight on individual gradient descent and less on consensus terms,and hence we can expect a longer time to overcome the state difference among agents;on the other hand,it also implies thateach agent’s trajectory suffers from less interference of neighbors,especially the error integration,which results in a smoother trajectory.

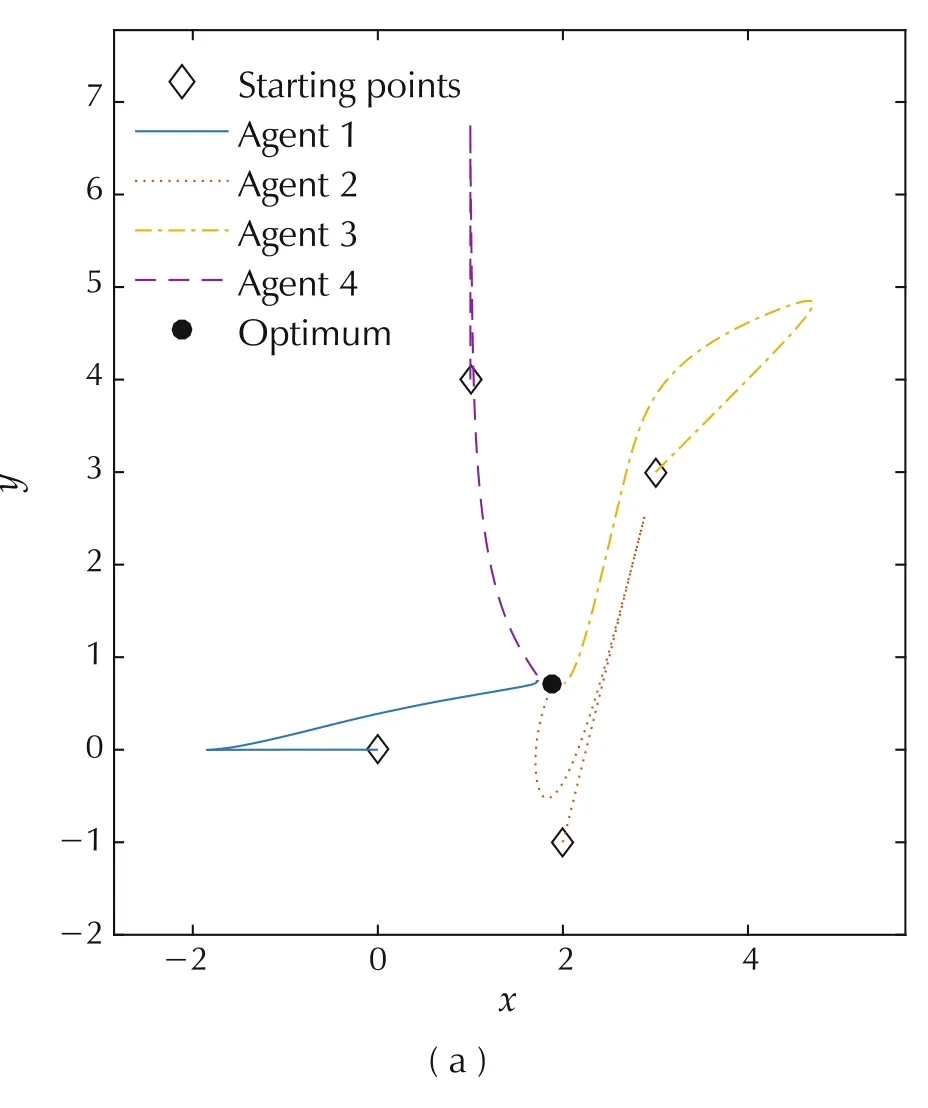
Fig.3 γ =0.1:kv=0.5,k g=kμp=0.0147,kp=0.00147,kμv=0.059.(a)Plane trajectories.(b)Maximum distance error.(c)Velocity evolution.(d)Acceleration evolution.

6 Conclusions

In this paper the distributed optimal consensus problem ofmultiple double integrators underbounded velocity and acceleration was studied.Each agent is assigned a convex function as individual cost,and a bounded distributed control law was proposed to achieve consensus at the optimum of the aggregate cost under bounded velocity and acceleration.Specifically,the control input consists ofa relative position errorterm,a damping term of its velocity,a gradient descent of its individual cost,as well as an integral feedback of the relative position and velocity error to correct the gradient differences.With the aid of quadratic Lyapunov functions,an exponentially fast convergence to the global optimum was established for strongly convex costs with Lipschitz continuous gradients,if the network is strongly connected and weight-balanced.Given the knowledge of the initial range of the optimum,the control gains were further properly chosen to satisfy the bounded constraints.A similar result holds when the relative velocity is not available.The case ofELdynamics was furtherdiscussed by the inverse dynamics control,assuming that the nonlinearity can be accurately known.In future we shall focus on the case when the a priori knowledge of the optimum is not available,or there exists uncertainty in the EL dynamics.