不完备序决策系统的约简一致性研究

陈一舟，王加阳，郑 娜

(中南大学 信息科学与工程学院，长沙 410083)

1 引 言

粒计算是当前智能信息处理中，通过模拟人的思维模式从而进行信息处理的一个新兴研究方向.波兰科学家Pawlak在20世纪80年代提出了粗糙集理论[1]，利用属性的等价关系形成的等价类作为基本的知识粒度，使其成为是一种能够处理不精确信息系统的数学工具.粗糙集中其他对象子集可以通过粗糙集的上、下近似算子来描述.经过三十多年的发展，粗糙集理论已经成为了粒计算的一个重要工具，在众多人工智能领域，如专家系统、机器学习、模式识别和决策分析等研究中得到了广泛的应用[2-4].经典粗糙集理论要求数据集中的每一个对象相对于每一个属性都有唯一确定的离散值，因此，经典粗糙集理论仅可以处理完备信息系统.

但是在实际情况中，由于测量误差、数据丢失等各种原因，我们所面临的信息系统往往是不完备的，并且许多属性带有偏好信息，比如商品价格、学生成绩等.因此，进一步丰富粗糙集理论，使其可以处理不完备序信息系统成为了粗糙集理论发展的一个重要方向.Greco[5-7]等人针对序信息系统中属性值之间递增或递减的序关系，提出了基于优势关系的粗糙集模型，给处理不完备信息系统提供了一种新的决策思路.

证据理论是进行不确定性推理的重要工具，基于人们对客观世界认识，根据人们已有知识对不确定性事件做出判断.证据理论是在概率论的基础上发展起来的，与传统的概率论相比，它能更好的把握所研究对象的模糊性和不确定性.D-S证据理论引入证据函数，将认知的“不确定性”和“未知不明”等概念区分开来，由信任函数与似然函数构建信任区间，用信任区间代替单个概率值来度量知识的不确定性.它在决策分析、模式识别、自动检测、社会计算、图像融合、安全分析、粒计算等领域得到了广泛的应用[8-15].

粗糙集理论和证据理论之间有着密不可分的联系[16]，粗糙集的上、下近似质量函数与似然函数和信任函数分别对应，证据理论中的信任函数可以由粗糙集的近似空间来描述，同时，粗糙集中的属性约简问题也可以通过信任函数来解决.粗糙集的优势在于它不需要先验知识，可以从已知的知识库中获取；而证据理论的优势在于可以进行不确定性推理，两者结合可以为研究提供了更多的解决方向.

目前，关于不完备决策系统的研究大多集中在优势关系的改进以及约简算法的设计上，关于其证据特征的研究较少.本文研究了在不完备序决策系统中，序上、下近似算子和证据理论中的信任函数和似然函数的关系，给出了如何根据序上、下近似算子来计算信任函数和似然函数的方法.另外，本文还提出了不完备序决策系统中在证据理论下，近似分布约简、相对信然约简以及相对分布约简的定义和相关性质，并研究了其一致性.

2 不完备序决策系统

2.1 不完备决策系统

决策系统为一个三元组S=(U，A∪{d}，f)，其中U是对象的非空有限属性集合，称为论域，A是非空有限属性集，{d}为决策属性集合，当条件属性集合和决策属性集合的交集为空集且决策属性值不存在缺失的情况时，该信息系统是一个决策系统.当决策系统中存在某些缺省或未知属性值时，用符号“*”或者“null”表示这个缺省值或者未知值.即当A∩{d}=Ø且d(x)≠*∩d(x)≠null时，三元组S=(U，A∪{d}，f)表示一个不完备决策系统.

定义1. 在不完备决策系统S=(U，A∪{d}，f)中，对于任意B⊆A，定义相似关系如下：

RB={(x，y)∈U×U|∀a∈B，f(x，a)=

f(y，a)∨f(x，a)=*∨f(y，a)=*}，

Rd={(x，y)|f(x，d)=f(y，d)}

其中对于任意x∈U：

RB(x)={y∈U|(x，y)∈RB}

Rd(x)={y∈U|(x，y)∈Rd}

由定义1可知，相似关系RB是自反，对称但非传递的，但相似关系Rd是一个等价关系.进而给出不完备决策系统中，基于相似关系RB的下近似和上近似：

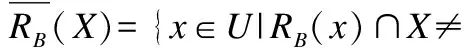
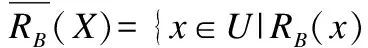
基于等价关系Rd的下近似和上近似为：

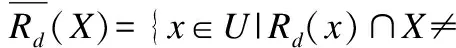
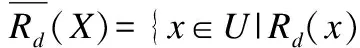
2.2 序决策系统

称二元组(L，≤)是一个全序(标记)集，非空集合L称为标记集，≤是L上的二元关系，需满足如下条件：

1)自反性：对于任意的x∈L，x≤x；

2)传递性：对于任意的x，y，z∈L，x≤y，y≤z蕴含x≤z；

3) ≤线性序：对于任意的x，y∈L，或者x≤y，或者y≤x.

定义2. 给定一个决策系统S=(U，A∪{d}，f)，如果条件属性集A中的每一个属性都是一个准则且决策属性d的属性值域是全序集，则称该决策系统是一个序决策系统，记作S≥=(U，A∪{d}，f).

假设属性a∈A是一个标准，优势关系≥a：x≥ay表示x至少与y一样优，x≥ay⟺f(y，a)≤f(x，a)(根据升序)或者≥a：x≥ay⟺f(x，a)≤f(y，a)(根据降序)，其中x，y∈U.对于任意属性子集B⊆A，定义x≥By⟺∀a∈A，x≥ay，它表示关于属性集A中所有属性，x至少与y一样优.式f(x，d)≥f(y，dB)⟺x≥dy表示就决策属性值而言，x至少与y一样优.一般而言，标准的值域可能是不连续的，但是其优先顺序是已经确定的或者是已知的.

定义3. 给定有序决策系统S≥=(U，A∪{d}，f)，对于任意B⊆A，关于B和d的优势关系定义如下：

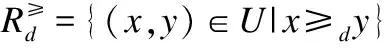
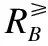
2.3 不完备序决策系统

定义4. 给定一个序决策系统S≥=(U，A∪{d}，f)，如果∃x∈U，a∈A，使得f(x，a)=*，则称之为不完备序决策系统，否则称之为完备序决策系统.

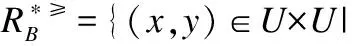
f(x，a)=*∨f(y，a)=*}，

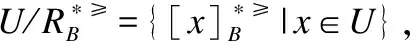
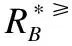
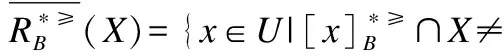
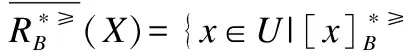
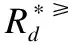
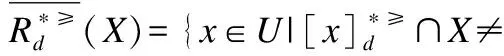
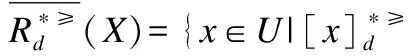
定义6. 给定一个不完备序决策系统S≥=(U，A∪{d}，f)，决策属性d的值域为Vd，为了方便，可假设Vd={1，2，3，…，L}，记为Clt={x∈U|f(x，d)=t}，则Cl={Clt|t∈Vd}是由决策属性d对论域U形成的一个划分.对t，s∈Vd，若t≥s，则任何属于Clt的对象都至少和任何属于Cls中的对象一样优.Clt的上并集和下并集分别表示为：

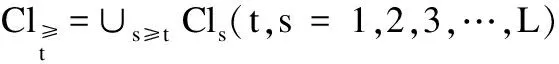
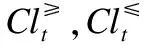
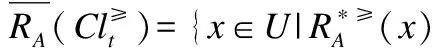
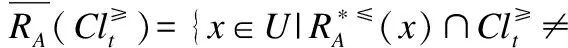
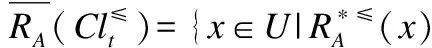
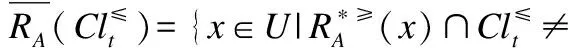
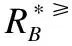
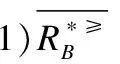
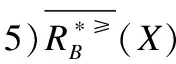
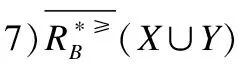
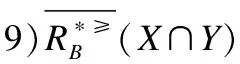
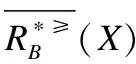
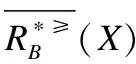
上述性质证明过程简单，均可由序决策系统的相关定义推理而得，故此处不再赘述.

3 不完备序决策系统的信任结构

证据理论用集合的形式表示命题，假设集合U包含了已知所有的证据，证据之间相互独立.证据理论通过信任函数和似然函数构建信任区间，可量化表达“不确定”和“不知道”的能力.

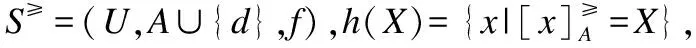
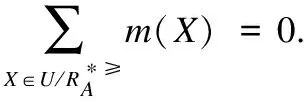
定义9. 给定不完备序决策系统S≥=(U，A∪{d}，f)，其信任结构是(M，m)，定义U上的信任函数Bel：2U→[0，1]如下：

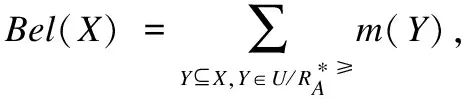
似然函数Pls：2U→[0，1]如下：

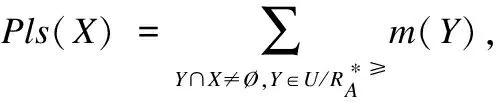
定理2. 给定有不完备序决策系统S≥=(U，A∪{d}，f)，对于任意X⊆U，B⊆A，似然函数与信任函数分别对应于基于优势关系的上、下近似质量函数，具体如下：

则其相应的基本概率分配函数如下：

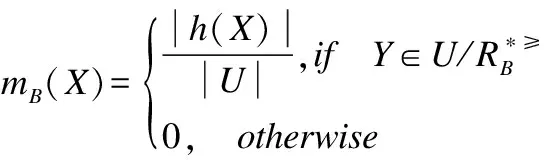
证明：首先证明信任函数Bel≥满足半可加性，对于任意X1，X2，…，Xn⊆U，我们有：

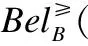
定理3. 表明，优势关系的上、下近似质量函数均满足半可加性，可作为证据理论中似然函数与信任函数.同理可得劣势关系的似然函数与信任函数.由此便可以通过序上下近似算子来得出序决策系统的信任结构.

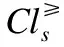
证明过程与定理2类似，在此不再赘述.

推论1. 定不完备序决策系统S≥=(U，A∪{d}，f)，B⊆A，对任意C⊆B，可得

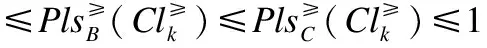
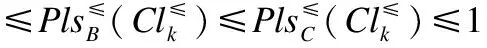
4 不完备序决策系统的属性约简

首先给出在不完备序决策系统中，近似分布约简的相关概念，然后给出在不完备序决策系统中，近似分布约简与信任约简和似然约简的等价性证明.

定义10. 设S≥={U，A∪{d}，f}是一个不完备序决策系统，其中A是条件属性集，d是决策属性，B⊆A，令

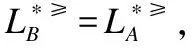
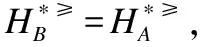
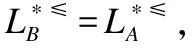
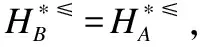
从定义10可看出，*≥上(下)近似分布约简是保持不完备序决策系统的每个决策类的向上合并的上(下)近似不变的属性子集，*≤上(下)近似分布约简是保持不完备序决策系统的每个决策类的向下合并的上(下)近似不变的属性子集.

下面给出不完备序决策系统的相对信任约简和相对似然约简的相关概念.

定义11. 设S≥={U，A∪{d}，f}是一个不完备序决策系统，其中A是条件属性集，d是决策属性，B⊆A，T={Cl1，Cl2，…，ClL}，

定理5. 设S≥={U，A∪{d}，f}是一个不完备序决策系统，B⊆A，则(1)B是相对*≥信任协调集，当且仅当B是*≥一下近似分布协调集;(2)B是相对*≥信任约简，当且仅当B是*≥一下近似分布约简.

证明：

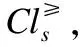
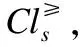
2)根据(1)可知其成立.

证毕

推论2. 设S≥={U，A∪{d}，f}是一个不完备序决策系统，B⊆A，则

1)B是相对*≤信任协调集，当且仅当B是*≤一下近似分布协调集;

2)B是相对*≤信任约简，当且仅当B是*≤一下近似分布约简.

证明过程与定理4类似，不再赘述.

定理6. 设S≥={U，A∪{d}，f}是一个不完备序决策系统，B⊆A，则

1)B是相对*≥信任协调集当且仅当B是相对*≤似然协调集；

2)B是相对*≥信任协调集当且仅当B是相对*≤似然协调集.

证明：

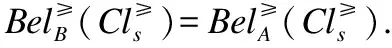
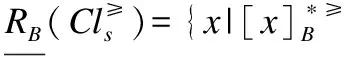
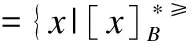
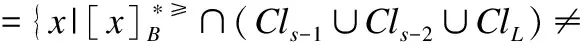
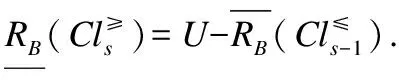
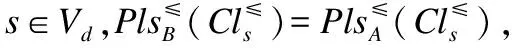
2)根据(1)可知其成立.

证毕

定理7. 设S≥={U，A∪{d}，f}是一个不完备序决策系统，B⊆A，则

1)B是相对*≤信任协调集当且仅当B是相对*≥似然协调集；

2)B是相对*≤信任协调集当且仅当B是相对*≤似然协调集.

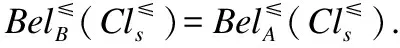
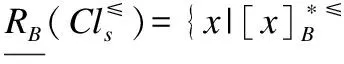
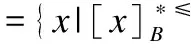
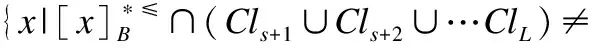
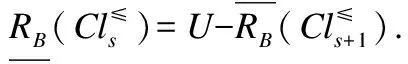
证毕

定理5、定理6和推论2证明了*≥(*≤)下近似分布约简是和相对*≥(*≤)信任约简是等价的，并且相对*≥(*≤)信任约简与相对*≤(*≥)似然约简也是等价的.

5 结 语

粗糙集模型是粒计算研究中的重要方法，它对于粒计算研究的推动与发展起着巨大的作用.从完备决策系统到不完备决策系统，从无偏好决策系统到有偏好决策系统，每种不同的决策系统所具有的特征都被不断的挖掘和发展，粗糙集理论也得到了越来越广泛的应用.本文介绍了不完备序决策系统的特征，研究了基于优势关系的不完备序决策系统与证据理论之间的关系，并给出了上、下近似与似然函数、信任函数之间的转换映射.接下来，提出了相对信任约简与相对似然约简的概念，并研究了它们之间的一致性关系，从而完善了不完备序决策系统的理论.以后我们将进一步讨论不完备序决策系统的知识表示、规则获取以及属性约简算法等.