一种联合LTR和社交网络的Top-k推荐方法

熊丽荣，王玲燕，黄玉柱

1(浙江工业大学 计算机科学与技术学院，杭州 310023)2(浙江理工大学，杭州 310018)

1 引 言

推荐系统可以有效地应对信息爆炸问题，越来越多的研究者将其作为学术研究的重点[1].大量研究利用用户-项目评分矩阵预测每个用户对每个项目的评分值，这些工作致力于提高全局评分预测精度即降低评分预测误差值，MAE和RMAE[2].推荐系统的最终目的是为目标用户提供一个排序的项目列表，但最小化评分预测值并不总能得到较好的top-k列表[3，4].因此，本文更关注于基于top-k的推荐[5]而不是基于评分预测的推荐.

如何为用户产生一个排序的项目列表被认为是Learning-To-Rank (LTR)[7]类问题，可以采用监督式的机器学习方法，从训练数据中得到用户特征信息，从而产生推荐结果.用户-项目评分矩阵是top-k推荐系统中至关重要的内容，然而，在现实生活中用户往往只会购买、评分小部分项目，这导致了top-k推荐系统由于缺少评分数据而不能产生较准确的推荐结果.另一方面相比于推荐系统产生的推荐结果，用户更倾向于朋友推荐的项目.将社会化网络中用户间的信任信息结合到top-k推荐算法当中可以缓解数据稀疏问题的同时提高用户对推荐结果的接受度.

本文结合社交网络信息，提出一种基于LTR的top-k推荐算法，BTRank相比较于已有的工作，本文有如下几个重要贡献：

1) 提出了一种新的信任计算模型，可以对信任信息做预处理，从全局、局部等多个方面挖掘用户间的潜在信任信息；

2) 考虑用户兴趣会随着时间发生变化，设计了时间衰减效应模型，根据时间对用户的评分数据进行处理；

3) 综合考虑用户对项目排序以及对信任用户排序时展现出来的兴趣偏好信息，构建用户特征矩阵，最终得到top-k推荐列表.实际数据集上的实验表明，本文的算法效果优于传统推荐算法以及同类的top-k推荐算法.

本文第2章阐述了相关工作.第3章详细介绍了本文提出的算法BTRank.第4章分析了本文算法的复杂性.第5章给出了实验与结果分析.最后第6章总结全文并指出未来的进一步工作.

2 相关工作

2.1 推荐系统

个性化推荐系统很好地满足了用户对个性化服务的需求，目前比较成熟的个性化推荐算法包括协同过滤推荐算法、基于内容的推荐算法及混合推荐算法三大类.

基于内存的协同过滤通过使用皮尔逊系数[12]等方式来计算用户间的相似度，并利用相似度过滤出近邻集合，最后基于这些近邻产生推荐结果.基于模型的协同过滤算法通过训练得到相应的特征模型，在数据稀疏情况下算法效果优于内存类协同过滤算法.矩阵分解可以将一个高维矩阵分解为两个低维特征矩阵的乘积，达到预测原矩阵空缺数据的效果，并且这两个特征矩阵的维度取值远远小于原矩阵的维度，因此在众多的模型类协同过滤算法中[17，25，26，30]矩阵分解是被最广泛使用的.本文的算法BTRank中也采用了矩阵分解方法.

基于内容的推荐算法[13]根据产品的特征描述和用户的购买历史信息，向用户推荐与他们购买过的产品有着类似特性的产品.一般适用于文本类的推荐，如新闻推荐、阅读推荐等.基于内容的推荐算法推荐结果过度单一，导致目标用户经常得到与曾经喜欢的项目类似的其他项目，推荐结果缺少多样性.

混合过滤算法将多种个性化推荐算法进行融合[14，15]，然而目前还是不能很好的将协同过滤推荐和基于内容的推荐算法进行拟合，并且算法的时间复杂度和空间复杂度都比较高，往往不能很好地满足实时性的推荐需求.此外，大多数的混合推荐算法都是基于假设用户是独立的个体的前提，忽略了社交网络中用户的朋友关系及信任关系，因此，准确度也不高.

以上三类算法是在目前的推荐领域内运用较为广泛的方法，研究者们主要用这些方法解决两大类问题：最小化评分误差、优化top-k项目排序.

2.2 基于评分预测的推荐

在实际生活中，用户往往只会购买并且评分小部分商品，所以用户-评分矩阵存在大量的“0”分数据，即评分数据存在严重的稀疏性.尽管基于模型的协同过滤算法可以有效地缓解该影响但是并不能完全去除数据稀疏对算法效果的影响.近年来，随着Facebook，Twitter等社交服务迅速发展，基于社会网络的推荐系统得到了越来越多的关注，很多研究者将社会化网络中的信任信息加入到推荐算法中以缓解用户数据稀疏问题.Jamali等人[16]结合基于内存以及基于模型的协同过滤算法，利用信任信息提出了随机走步框架.该算法可以在较短的路径中得到更精准的评分预测值，同时还可以提高推荐结果的覆盖率.Ma等人[17]首次提出了联合概率矩阵分解(Unified Probabilistic Matrix Factorization，UPMF)方法，在方法的训练模型中，评分矩阵和信任矩阵共享用户特征矩阵，从而能够结合这两面信息进行推荐.

然而，用户更希望看到一个符合自己兴趣爱好的top-k项目推荐列表，上述算法主要致力于最小化评分预测误差值RMSE和MAE，并不能得到一个更好的top-k排序列表.本文的研究重点在于如何找到一个更好的top-k列表.

2.3 基于top-k排序的推荐

已有的一些较好的top-k推荐方法，利用LTR算法思想[7]，从训练数据生成个性化排名列表.基于LTR的top-k推荐方法分为list-wise和pair-wise两类.Pair-wise模型通过用户购买、浏览信息训练其对每个项目对的相对偏好[18，19].Pair-wise模型在top-k推荐方面已经取得了实质性的改进，但存在着高计算复杂度的问题.List-wise模型具高可扩展性[19，20]和较低的计算复杂度，该模型是基于实际排序列表和预测列表之间的差距来优化预测每个用户的项目排名推荐列表.

将社会化网络中的信任信息加入到推荐算法当中，可以缓解评分数据稀疏性问题，同时提高推荐算法的准确度[8，9，21，30].文献[9]中提出了一种基于pair-wise的LTR方法，该文主要基于以下假设：相比于用户根本不知道的项目，他们更倾向于其朋友喜欢的项目.然而，他们的方法不能直接处理数字评分，并且由于pair-wise模型的内在特性，该算法具有较高的计算复杂度.Yao等人[8]采用文献[22]中的评分模型，将用户的兴趣爱好和其朋友的兴趣爱好线性结合，建立了评分预测模型.与本文一样他们也通过使用top-one概率(这将在本文第3章中解释)来降低算法的复杂度.然而，他们只关注用户对物品评分时存在的兴趣偏好，忽略了用户对朋友进行信任打分时展现出来的兴趣偏好信息.Park[21]等人 中提出了TRecSo算法，从信任、被信任两种角色来考虑用户的特征向量，同时也将信任信息对top-k排序列表的影响考虑进算法当中，构建了一个出色的训练模型.但是该算法对于用户间信任处理过于简单，只考虑了用户的出度、入度信息，同时由于TRecSo模型中用户特征向量由多个向量组成，导致模型的训练复杂度有所上升.

在本文中，我们结合评分、信任信息提出了基于list-wise思想 BTRank算法.在算法模型训练前期我们将从多方面来重组用户间的信任信息，模型训练时使用top-one概率来优化算法的性能.最后我们在两个现实世界数据集上证明，BTRank要优于以上几类优秀的方法.

3 基于信任的top-k算法BTRank

为了更好地了解本文提出的算法，本章中3.1节简短的介绍核心top-one概率模型，3.2节中提出本文的时间效应模型，之后3.3以及3.4节分别介绍如何在评分、信任信息中应用top-one概率模型.最后3.5节展示如何结合评分、信任两部分信息，给出BTRank模型的目标函数.

3.1 Top-one概率模型

Plackett-Luce模型[23]可以用于计算每个用户对曾经评分过项目的排列分布概率.该模型基于假设：每个不同的项目排列都有相应的分布概率，而高的排列概率意味着该项目排序更受用户喜爱.

排列概率：对于用户ui，给定含有M个项目的集合V，π={v1，v2，…，vM}是其中一种可能的项目排序，其对应的评分信息为{ri1，ri2，…，riM}，那么π排列的分布概率为：

(1)

其中rij是用户ui对项目vj的评分值，exp(r)=er.根据公式(1)可知，对于含有M个项目的集合来说，每个用户都有M!种不同的项目排序，计算复杂度太高.为了解决这个问题，我们使用top-one 概率来代替公式(1)中的排列分布概率：

(2)

由于用户更关心系统推荐给他的top-k个项目，因此本文在考虑项目可能排序时只关注前k个项目.公式(2)代表对于用户ui来说项目vj被排列在第一位的可能性.

3.2 时间效应模型

传统的推荐算法，将所有的项目平等对待，没有考虑用户的兴趣会随着时间的演变产生变化，致使推荐精度不高.根据19 世纪德国心理学家赫尔曼·艾宾浩斯的实验结果可得知，遗忘在记忆后会立刻开始，并且遗忘速率遵循先快后慢的规律.他根据实验结果将时间与记忆量的关系绘制成了著名的艾宾浩斯遗忘曲线[29]：

图1 艾宾浩斯遗忘曲线Fig.1 Ebbinghaus forgetting curve

学者Ding也认为资源的时效性随时间的变化应是一种指数衰减的过程[28]，因此结合图1我们设计资源衰减的时间效应模型为：

h(Δt，λ)=e-λΔt

(3)

其中Δt∈[0，+∞)表示学习过后经过的时间，λ代表遗忘速率，不同人群的λ可能不同，h为到目前位置记忆的衰减比例.用户可以分为两类：

1)念旧型，喜欢一类事物的周期很长，一段时间内兴趣爱好变化不大；

2)多变型，喜欢尝试新事物，兴趣爱好随时间呈现跳变型.在推荐系统中，评分信息可以很好的反映一个人的兴趣爱好变化，本文以3个月为一个周期，统计用户从第一次评分到目前为止所有周期内平均评分的变化值作为该用户的遗忘速率λ.

3.3 评分模型

基于矩阵分解框架，用户ui对项目vj的预测评分计算方法如公式(4)所示：

(4)

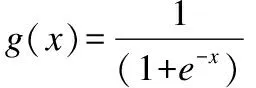
但是公式(4)中并未考虑时间因素对用户评分的影响，考虑时间效应后，改写公式(4)，得到用户ui在时间ti，j对项目vj的预测评分计算公式：

(5)

同时为了解决用户评分数据的稀疏性，本文在计算预测评分的模型中加入信任用户间的影响，更新公式(5)如下所示：

(6)

sik表示用户ui对uk的信任评分值，T(i)是用户ui信任的用户集合.参数β用于平衡控制信任用户对目标用户评分的影响程度，β∈[0，1].当β=1时表示完全没有影响，反之β=0表示用户对项目评分完全受信任用户影响.

此时我们可以利用公式(2)的top-one 概率模型以及交叉熵公式得到目标函数，最小化预测排序列表与真实排序列表间的不稳定性：

(7)

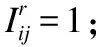
3.4 信任模型

本文提出了一种新的信任计算模型，使用全局、局部两个方面来刻画用户间信任信息.在计算对来说uj的全局信任gtij时，不同于已有的研究，本文主要考虑以下三点：

1) 其余所有用户对uj的信任评价值；

2) 对uj有信任评价的用户数量：

3)ui与这些用户之间的兴趣相似度.最终本文构建全局信任计算公式如下所示：

(8)

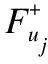
本文在计算与uj的局部信任ltij时，分两种情况进行考虑：

1)对uj有信任评分值，即对uj存在直接信任，那么对uj间的局部信任基于直接信任进行计算得到；

2)对uj没有信任评分值，根据信任传播性得到对uj的间接信任值作为局部信任值.为了消除用户间评分的习惯差异性，本文对数据集中用户间的直接信任评价值进行以下处理：

(9)

(10)

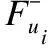
本文主要利用信任传递性来计算用户间间接信任评价值idtij.公式(11)为信任衰减函数，L是信任传递路径长度，其中最大路径长度Max_Hop<=6：

(11)

本文选取最有效路径[6]而不是最短路径作为用户间最佳的信任传播路径.同时将网络中所有用户间平均信任值作为判断的信任阈值Υ.当某条路径上存在两个相邻用户间的信任评价值小于Υ时，则放弃该条路径重新寻找有效路径.某条路径Pathi的源节点ui对目标节点uj的信任评价值计算如公式(12)所示：

(12)

其中uk代表路径Pathi中第K个节点，Tuk-1→uk表示节点uk-1对uk的信任评价值，当信任值大于阈值Υ时，Iuk-1→uk为1，反之为0.当网络中存在多条有效路径时，本文选取信任值最大的一条，如公式(13)所示：

(13)

综上所述，用户间的最终信任值计算公式如(14)所示，其中α∈[0，1]为平衡参数，用于调和全局信任以及局部信任间的比重.

sij=αgtij+(1-α)ltij

(14)

当用户ui对uj只存在间接信任关系，考虑到此时的局部信任比全局信任要可靠的多，特别是在全局网络中对uj有过信任评分的用户数量稀少的情况下.所以此时α的计算公式如下所示：其中F+(uj)表示网络中信任uj的用户集合.

(15)

以上是本文提出的信任模型的全部内容，它主要用于对信任的前期处理，对于训练过程中ui对uj的信任值可以根据公式(16)构建：

(16)

Ui是用户ui的特征向量，Tj是用户uj的信任特征向量.同样地，对于用户间信任评分数据也可以用熵公式来衡量真实训练排序以及预测排序之间的差异，最小化熵公式如下所示：

(17)

3.5 目标函数

在3.3、3.4节中，本文定义了如何将评分、信任信息模型化，最后本文使用公式(18)将公式(7)与公式(17)联合进一个统一模型当中，并将其作为目标函数：

(18)

为了降低模型复杂度，本文设置λu=λv=λt=λ.同时为了得到相应的特征向量，本文采用随机梯度下降法来得到它们的局部最优值，其计算公式如下所示：

(19)

(20)

(21)

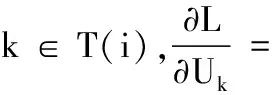
(22)

(23)

(24)

(25)

(26)

其中g′(x)是逻辑斯蒂函数g(x)的导数，g′(x)=exp(x)/(1+exp(x))2.

4 复杂性分析

BTRank的计算开销主要来自于公式(14)中前期信任关系的训练、公式(18)中目标函数L的计算以及公式(19)-(26)中各个特征向量对应的梯度下降的计算.在训练信任关系时，我们假设存在信任数据的用户数量为t，且每个用户的邻居集合大小为N，则间接信任关系的训练时间复杂度为O(t2N)，其中N通常较小，可以认为是常数，则时间复杂度趋向于O(t2)；目标函数L的时间复杂度为O(pRl+pSl)，其中pR，pS分别表示矩阵R，S中非零元素个数，由于数据稀疏性，pR和ps都很小；梯度下降法中计算复杂度主要由公式(19)-(21)产生，其时间复杂度分别为O(pRk+pSk)，O(pRk)和O(pSk)，k表示最终推荐给用户的top-k目表中的项目个数，因此每次迭代的总时间复杂度为O(pRk+pSk).假设本文算法迭代d次，总的时间复杂度为O(t2)+O(dpRk+dpSk)，因此，与pair-wise的LTR方法不同，我们提出的模型可以有效地应用到大规模数据集中.

5 实验与结果分析

在本章节中设计了几个实验将本文的算法BTRank与其余几个出色的算法进行比较.实验的设计主要基于以下几点：

1.如何将本文算法与已有优秀算法进行比较？

2.考虑时间因素是否可以提升算法的精度？

3.模型训练前使用第3.4节中提出的信任模型对信任数据做处理是否对算法有所帮助？

4.参数β对算法推荐准确率有怎样的影响？

5.特征向量U、V、T的维度取值对推荐准确率有什么影响？

5.1 数据集

在实验中，我们使用两个公共现实世界的数据集Epinions*http://www.trustlet.org/wiki/Extended_Epinions_dataset和Ciao*https://www.librec.net/datasets.html，每个数据集都包含用户项目评分、用户之间的信任关系(数据集中的信任关系都是不对称的)和评分的时间信息，其中项目评分是区间[1，5]内的整数.

5.2 实验规则

对于每位用户我们分别随机选取n=10，20，50条项目评分和信任记录作为训练数据集，余下的都作为测试数据.为了保证每位用户至少存在10条测试数据，我们会相应的过滤掉数据记录少于20，30，60条的用户.

参数设置：对于所有的对比实验，本文均按照原文设置最优参数；在算法BTRank中，我们设置λ=0.1，γ=0.01，其中γ是迭代过程中的学习速率，所有的实验结果都是5次实验的平均值.

5.3 评价函数

均方误差(RMSE)和平均绝对误差(MAE)是传统推荐系统的标准评估指标，这两个指标能衡量真实评分与预测评分之间的差距，但是不能是评价top-k项目列表排序准确性.本文旨在提高top-k推荐质量，因此使用信息检索领域最常用的指标NDCG、Recall、Precision作为本文评价标准.

NDCG更加重视排序列表的前几位，排序越前面的项目在评估中所占比重越大.对于排序在第一位的项目来说，得到5分与得到4分评分相比，前者的NDCG@1更高.所以对于ui来说，k个项目排序列表的 NDCG值为：

(27)

其中Z是一个常量，它使对于ui来说最优的top-k排序的NDCG为1.

最后我们计算所有用户的NDCGi@K值并取平均值得到NDCG@K如下所示：

(28)

其中|U|是用户集合U的大小.

Precision@K表示推荐精准度，Recall@K表示召回率，对于ui，集合Pi={v1，v2，…vK}表示由推荐系统产生的top-k项目列表，Qi={v1，v2，…vz}表示实际用户偏爱项目，则

(29)

(30)

5.4 对比实验

本文跟以下三类出色的推荐算法对比：传统CF方法，仅基于评分的LTR方法和基于社交网络的LTR方法.

a)传统CF方法

UserKNN[27]：一种基于用户相似度的传统协同过滤推荐算法.

b)基于评分的LTR方法

BPR[18]：结合矩阵分解方法的pair-wise类LTR算法.

ListRank[19]：结合矩阵分解方法的list-wise类LTR算法.

c)基于社交网络的LTR方法

SBPR[9]：在BRP的基础上加入信任信息，提高算法准确度.

SoRank[8]：结合信任信息的list-wise类LTR算法，线性结合信任用户对目标用户的影响，从而优化top-k推荐算法效果.

BTRank：本文提出的算法.

5.5 信任模型的作用

为了验证3.4节中提出的信任模型的有效性，我们设计了多个对比实验，将本文算法BTRank与未应用信任模型的BTRank进行比较，实验结果如图2所示.从图中可以看出，在各种情况下使用了信任模型的算法结果明显好于未使用的算法结果，证明了本文信任模型对算法有推进作用，在算法训练之前对信任数据做预先处理是必要的.

5.6 时间效应模型的作用

本文在3.2节中，根据艾宾浩斯遗忘曲线提出了一个时间效应模型，对用户的评分数据根据历史时间给予相应的权重，越接近当前时间的评分数据其权重值越高，反之则越小.

为了验证该模型的有效性，我们设计了多个对比实验将本文算法BTRank与未应用该时间效应模型的BTRank进行比较，实验结果如图3所示.从图中可以看出，在各种情况下使用了时间效应模型的算法结果明显好于未使用的算法结果，证明了该模型对算法有推进作用，考虑用户评分数据时间效应性是有必要的.

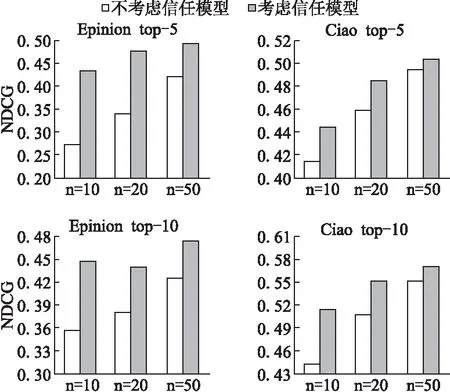
图2 信任模型的影响Fig.2 Impact of trust model

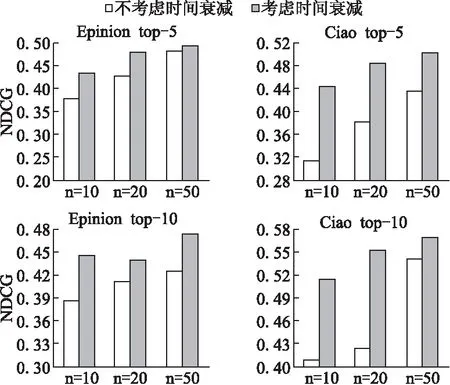
图3 时间模型的影响Fig.3 Impact of time attenuation model

图4 参数β的影响(n=20，k=5)Fig.4 Impact of parameter β (n=20，k=5)

5.7 参数β的影响

在文本算法BTRank中参数β用于控制信任用户兴趣爱好对项目评分的影响.本次实验训练数据选取规则采用n=20，结果如图4所示.在不同数据集上算法效果趋势各不一致，但是大体上都呈先上升后下降趋势.其中β=0.4是一个阈值，当β<0.4时，算法效果呈上升趋势，β>0.4时算法效果呈下降趋势，所以此时将β值设为0.4使得算法效果最优.

5.8 特征维度的影响

矩阵分解算法复杂度随着特征维度取值增加而增加，本文为了降低模型训练的时间，在区间[1，50]上探寻局部最优的维度取值，实验结果如图5所示.根据结果可以看出，虽然算法效果趋势都不完全一致，但是都呈先上升后下降的趋势，在特征维度值取为5的时候达到最佳效果，所以在本文之后的实验中我们将维度设置为5.

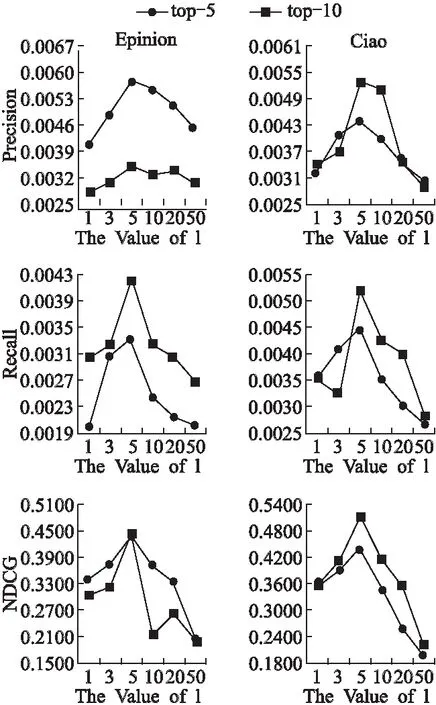
图5 特征维度取值影响(n=10，k=5)Fig.5 Impact of latent dimensionality (n=10，k=5)

5.9 算法比较

为了验证本文算法的有效性，本实验将BTRank与其余五个算法进行比较，结果如图6所示.从图中可以看出本文算法BTRank的效果在各种不同情况下普遍好于其余算法，而UserKNN算法效果明显弱于其它算法，很好地说明传统的个性化推荐算法并不适用于top-k推荐.

BTRank、SoRank、ListRank-MF均是基于list-wise的LTR类算法，其中ListRank-MF算法未考虑信任用户对目标用户的影响，而SoRank和本文算法均考虑到了信任关系的影响，并且从实验结果中可以明显看出这两个算法效果好于ListRank-MF，说明同时考虑自身以及朋友因素对评分构成的影响可以有效提升算法的效果；相比于SoRank，本文算法不但考虑用户对项目排序展现出来的兴趣偏好，同时联合考虑用户对朋友信任排序时的偏好信息，从而构建更准确的用户特征矩阵.从这两个算法的对比效果可以看出本文算法明显好于SoRank，可见综合考虑用户对项目、朋友排序时的偏好可以有效提高算法效果.

其中BPR以及SBPR均是基于parie-wise的LTR类算法，这两个算法与BTRank、SoRank、ListRank-MF对比，虽然整体效果要弱于list-wise类算法，但是并不明显，说明pair-wise在top-k推荐中也获得了较好的效果，但是相比于list-wise类算法还是略逊一筹.

6 总结与展望

本文提出了一种基于信任的LTR类推荐算法BTRank，通过加入社交网络中信任信息来缓解数据稀疏问题、优化top-k排名预测精度.具体来说，本文首先使用信任模型重构用户间的信任信息，其次设计时间衰减函数分阶段评估用户兴趣变化，同时在预测用户评分时考虑信任用户对目标用户的影响，最终结合用户对项目评分排序以及对其他用户信任评分排序时产生的偏好信息，构建更准确的用户特征矩阵从而得到较好的top-k推荐列表.综合实验结果表明，BTRank推荐的top-k项目列表在准确度方面显著优于传统的推荐算法以及同类top-k推荐算法.

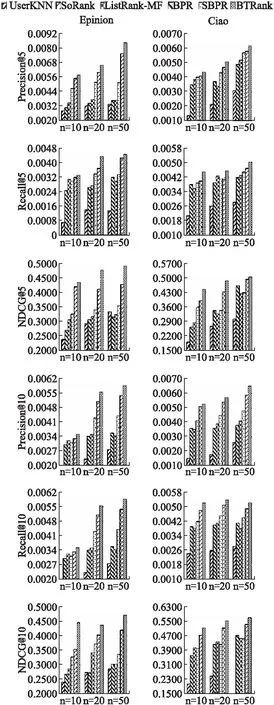
图6 不同算法效果对比Fig.6 Comparison of different algorithms

为了降低算法的复杂度，本文提出的BTRank是基于项目top-one 概率而不是top-k概率.在未来的工作中可以研究更好的项目排序概率模型用于top-k排序推荐；其次希望可以研究出更好的时间衰减模型，能更准确地衡量评分数据十分稀少的用户兴趣变化.