融入柯西扰动的改进差分进化算法及其应用
2019-01-24邹德旋
沈 鑫,邹德旋,张 鑫,胡 震
(江苏师范大学 电气工程及自动化学院,江苏 徐州 221116)
1 引 言
差分进化(Differential Evolution,DE)算法[1]是一种智能优化算法,不需要问题具有连续性和可微性,因此被证明具有良好的适用性.目前,DE算法在约束优化[2]、多目标优化[3]、电力系统经济调度[4]等方面得到了广泛的应用.
与其他智能优化算法类似[5,6],DE算法也存在早熟收敛和收敛精度低等缺点,特别是解决高维、时变问题时表现的更为明显.为此,学者们从不同角度提出了相应的改进,这些改进大致归为以下三类:一是对DE算法本身机制的改进,如初始化种群、参数、变异策略、交叉策略和边界处理.Zou等[7]在初始化种群时建立了一种外部存档,外部存档中优秀个体将被选择进入种群参与进化.Yi等[8]对缩放因子和交叉率进行自适应调整,避免了参数选择的麻烦.Islam等[9]使用新的变异算子DE/current-to-gr_best/1、参数选取机制和交叉操作中个体选择方式.Zhang等[10]使用四种边界处理手段以适应不同的实际问题.二是加入一些优良的机制,如重新开始机制等.Tian等[11]提出一种新的开始机制增强了种群多样性和对优秀个体的探测.三是将DE算法与其他优化算法结合,如粒子群与人工蜂群融合的算法[12]等.以上改进措施一定程度上避免了算法陷入局部最优并提高了算法的收敛精度,但是算法的全局寻优能力仍有很大的提升空间.
为了进一步增强算法的全局寻优能力,提出了融入柯西扰动的改进差分进化算法.该算法对基本DE算法做了深度改进,并通过优化19个测试函数和2个电力系统经济调度问题,验证了该算法的有效性.
2 基本差分进化算法
差分进化算法是一种并行算法,其主要操作是首先种群在搜索空间内初始化产生,然后进行变异、交叉、选择操作,更新种群.基本差分进化算法的步骤如下:
1)初始化
DE算法随机初始化产生NP个D维分量的个体.
xi,0=(xi1,0,xi2,0,…,xiD,0),i=1,2,…,NP
(1)
xij,0=Lj+rand ·(Uj-Lj),j=1,2,…,D
(2)
其中,Lj表示xij的下限,Uj表示xij的上限;xij,0表示初始代第i个体的第j维分量;NP表示种群数量;D表示个体的维数;rand 表示在(0,1)区间上均匀分布的随机数.
2)变异
DE算法通过对目标个体xi,G进行扰动产生变异个体vi,G+1,在DE中最常用的变异策略是DE/rand/1,除此之外还有DE/best/1、DE/current-to-best/1、DE/current-to-rand/1等变异策略.
DE/rand/1:
vi,G+1=xr0,G+F·(xr1,G-xr2,G)
(3)
DE/best/1:
vi,G+1=xbest,G+F·(xr1,G-xr2,G)
(4)
DE/current-to-best/1:
vi,G+1=xi,G+F·(xbest,G-xi,G)+F·(xr1,G-xr2,G)
(5)
DE/current-to-rand/1:
vi,G+1=xi,G+F·(xr1,G-xi,G)+F·(xr2,G-xr3,G)
(6)
其中,F为缩放因子;r0,r1,r2表示1,2,…,NP上两两互不相同的随机整数并且均不等于i;xi,G表示第G代的第i个体;vi,G+1表示变异个体;xbest,G表示第G代的最优个体.
3)交叉
父代个体xi,G和变异个体vi,G+1进行交叉操作得到试验个体ui,G+1=(ui1,G+1,ui2,G+1,…,uiD,G+1).
(7)
其中,CR为交叉率;jr表示1,2,…,D上的随机整数,用来确保vi,G+1中至少有一个分量保留至下一代,实现种群进化.
4)选择
选择操作是基于贪婪原则选择试验个体和父代个体,对于最小化问题,适应度值越小的个体越优秀,优秀个体将进入下一代.
(8)
其中:xi,G+1表示经过选择之后进入下一代的个体.
3 融入柯西扰动的改进差分进化算法
基本DE算法存在早熟收敛和收敛精度低等缺点.为了解决这些缺点,学者们从不同角度对算法做了大量的改进.借鉴学者们的改进,这里将在DE算法中加入最优个体信息复制机制和小概率扰动并对DE算法的变异策略、交叉策略和控制参数做如下的改进.
3.1 变异策略的改进
3.1.1 双策略变异
DE算法是一种全局搜索算法,种群中所有个体随着迭代的进行都逐步向全局最优个体靠近.在算法进化的开始阶段,应尽可能使算法在搜索空间内充分的探测,保证种群多样性.而到了算法进化的后期,应充分挖掘最优个体的信息,加速种群收敛.因此,在算法的整个生命周期内变异策略固定不变对算法的性能往往是不利的,针对算法各个搜索阶段特性的不同,学者们使用的一种方法是使用多变异策略.Li等[13]使用了两个变异策略,一个是基于随机个体,另一个是基于最优个体,进化前期基于随机个体的变异策略被选中的概率大,而到了进化后期基于最优个体的变异策略被选中的概率大,有效平衡了算法的全局搜索和局部搜索能力.借鉴前人的研究,新算法使用了一种双策略变异算子,不同进化时期,每个变异策略在整个变异算子中所占的比重不同.变异算子的表达式如下:
w=wmin+(wmax-wmin)·(G/Gmax)
(9)
vi,G+1=(1-w)·(xr1,G+F·(xr2,G-xr3,G))+w·(xi,G+F·(xbest,G-xi,G)+F·(xr4,G-xr5,G))
(10)
其中,wmin和wmax分别取0和1,w随着进化的进行线性递增.Gmax表示最大进化代数;当G=1时,此时变异算子近似为DE/rand/1,当G=Gmax时,此时变异算子变为DE/current-to-best/1.r0,r1,r2,r3,r4,r5表示1,2,…,NP上两两互不相同的随机整数且不等于i.
式(9)通过参数w动态调整两种变异策略的比重,适应了整个进化过程.
3.1.2 柯西扰动
由于DE算法易陷入局部最优,因此随机改变算法的进化方向是一种避免陷入局部最优的有效措施.张锦华等[14]使用rand随机数扰动当前最优个体达到改变粒子的进化方向,以便粒子向全局最优个体靠近.这里使用柯西分布产生的随机数扰动最优个体xbest,G,避免算法陷入局部最优.柯西分布的图形似一个钟形,两翼宽,加大了寻优范围.为了显示柯西扰动的优势,将在第5部分详细比较柯西扰动与rand随机数产生的扰动所引起算法性能的差异.柯西随机数表达式如下:
ci~randci(μ,λ)
(11)
其中,ci表示个体i所对应的柯西随机数;randci表示个体i所对应的柯西分布函数,μ和λ是其局部参数,这里均取0.1.
3.2 小概率扰动
为了进一步增强算法跳出局部最优的能力,这里使用了一种小概率扰动[15],个体以某种概率在搜索空间内随机产生.小概率扰动流程如下:
if rand vi,G+1=(1-w)·(xr1,G+F·(xr2,G-xr3,G))+ w·(xi,G+F·(ci·xbest,G-xi,G)+F·(xr4 ,G-xr5 ,G)) else vi,G+1=L+rand ·(U-L) end 其中,L和U分别是种群搜索边界的下限和上限;Pr一般为很大的小数,这里取0.99. DE算法原始交叉策略是根据交叉率决定是父代个体保留至下一代还是变异个体遗传给下一代.为了提供更好的个体,学者们使用其他个体替换交叉策略中的父代个体.Islam等[9]使用一种线性递减机制从当前种群中随机选取的个体取代父代个体.这里联合当前中心解和最优解来取代父代个体,中心解源自于Liu等[16]提出的中心粒子群优化算法,并被Zou等[7]用于DE算法提供一个潜在的搜索方向.中心解及交叉策略表达式如下: (12) (13) 其中,xcenter,G表示第G代的中心解,而xcenterj,G表示中心解的变量,(13ii)中的新个体分量取代父代个体分量,有效引导个体向好的方向进化. DE算法类似于达尔文主义的适者生存理论,优秀个体存活,那么优秀个体所包含的信息也势必对种群的进化是有利的,这里使用当前最优个体的z维数值替换当前最差个体对应的z维数值,有利于扩大最优个体的影响力,改善最差个体,充分挖掘了种群中的优秀信息.图1为该机制的示意图. 图1 最优个体信息复制机制示意图Fig.1 Diagram of the optimal individual information replication mechanism 控制参数F和CR对DE算法的性能有很大影响,通常取固定值,这样不适用于各种问题以及算法搜索的全过程.优秀的参数值更可能产生优秀的个体,因此,优秀的参数值应保留至下一代,这里将试验个体与目标个体比较,若个体进化成功即对于最小化问题试验个体适应度值小,则缩放因子和交叉率继承上一代的值,否则F在[Fmin,Fmax]内重新产生且CR重新产生为高斯分布的随机数.调整缩放因子和交叉率的表达式如下: (14) (15) 其中,Fi,G+1表示第G+1代第i个体的缩放因子;Fi,G表示第G代第i个体的缩放因子;CRi,G+1表示第G+1代第i个体的交叉率;CRi,G表示第G代第i个体的交叉率;Fmin是缩放因子的最小值;Fmax是缩放因子的最大值;randni(m,δ)表示平均值为m和标准差为δ的高斯分布函数,若CR值落在[0,1]之外,则CR重新产生;对于初始代F和CR分别使用(14i)和(15i)随机产生. CDMDE算法的流程如图2. 电力系统经济调度(ELD)问题[17]是在满足系统运行约束条件下优化发电机组间功率分配,使系统发电成本最小化 图2 CDMDE算法的流程Fig.2 Flow chart of the CDMDE algorithm 的问题.因此,解决ELD问题主要包括两方面,一是使系统发电成本最小化,二是满足系统运行约束. 系统发电成本的目标函数是一个多项式函数,其通常被描述成一个二次函数或二次函数和正弦函数的组合,具体表达式如下: (16) (17) ELD包括了不等式约束和等式约束,不等式约束是发电机组输出功率的上、下边界,等式约束是所有发电机组的电力输出等于系统总的负载需求和传输损耗.具体描述如下: (18) (19) 罚函数法是处理ELD约束条件的常用方法,但往往得不到满意的解,这里使用了Zou等[4]处理约束的方法,该方法首先对不可行解进行修复,然后使用罚函数法进一步处理等式约束. 为了显示新算法的优化性能,这里将选取19个测试函数[18-20]对CDMDE算法性能进行测试,测试结果与近期著名的DE算法进行对比,19个测试函数如表1所示,变量范围及理论最优值见文献[18-20].同时对算法改进部分做了如下研究:研究CDMDE算法中柯西扰动和小概率扰动的作用;研究改进交叉策略的作用;研究最优个体信息复制机制的作用;将CDMDE算法中的算子与几种典型的变异算子进行对比实验.这四种算法改进部分的实验参数与函数20维数时不同算法对比实验参数一致.除此之外,将CDMDE算法用来优化3机组[21]和38机组[22]ELD问题,并将他与文献中的结果进行对比分析.所有对比实验结果都用Matlab8.3仿真软件实现,且实验的电脑配置为Intel(R)Core(TM)i5-2450M CPU @ 2.50GHz.各算法独立运行30次. 将CDMDE算法与基本DE算法和几种著名DE算法HSDE[8]、RMDE[15]、SPS_DE/rand/1[23]进行比较.另外,CDMDE算法与其他DE算法之间使用平均值、标准差和以显著性水平为0.05的t-test指标[24]得出他们性能的优劣,若经t-test分析得出两种算法有差异,那么使用一种胜率求出他们的优劣,两种算法每次运行的最优值两两比较,胜的一方得1分,平的双方各得0.5分,败的一方不得分,求出每个算法得到的总分再除以总的比较次数就是他们各自的胜率,总共经过900次比较,这里将对比算法分别与CDMDE算法比较.各算法的参数设置如下:HSDE、RMDE和SPS_DE/rand/1的参数与对应的文献一致;基本DE算法中F=0.5,CR=0.9,变异策略DE/rand/1,二进制交叉操作;CDMDE算法中参数z=10,Pr=0.99,wmin=0,wmax=1,缩放因子的最大值和最小值分别为0.9和0.1,柯西分布的局部参数μ和λ均为0.1,高斯分布的平均值m=0.8和标准差δ=0.5;所有函数的维数分别取20、50和100维;函数f8和f19最大进化代数Gmax=100,其余函数的最大进化代数Gmax=1500;种群数量NP=100.算法优化结果见表2和表3,其中“+”、“-”和“=”分别表示比较算法性能优于、劣于和相近于CDMDE算法.NOBM和NOBSTD分别表示某算法取得最优平均值和最优标准差的函数个数,最优平均值和最优标准差分别表示优化某个函数时某算法的平均值和标准差不差于其他算法. 从表2和表3可以看出,CDMDE算法性能与其他算法相比占绝对优势.在不同维数下,CDMDE算法的NOBM和NOBSTD远大于其他算法,说明CDMDE算法对大多数测试函数的平均优化性能和稳定性远好于对比算法.四种对比算法中,RMDE算法的NOBM和NOBSTD不低于其他对比算法,HSDE算法在中高维时NOBM与RMDE算法接近且两个算法的NOBSTD相同,其他两种对比算法的NOBM和NOBSTD最低甚至为0,因此就平均值和标准差而言,对比算法中的RMDE算法整体性能最优.一般而言,对于不同算法求解同一个函数,如果某一算法的平均值和标准差都最小,那么该算法性能最佳,上述几种算法对大多数函数可以达到平均值和标准差同时最优.对不同维数下的函数f8、f15、f16和f19,CDMDE算法均可找到它们的全局最优值.此外对于函数f5和f12,CDMDE算法在低维时无法找到它们的全局最优值,但该算法在中高维时能找到它们的全局最优值,因此,对于某些优化函数,CDMDE算法在更高维时表现更好.从t-test指标可以看出,对大多数函数四种对比算法劣于CDMDE算法. 表1 19个测试函数 函数f1(x)=∑Dj=1x2jf2(x)=∑Dj=1|xj|+∏Dj=1|xj|f3(x)=∑Dj=1(∑jq=1xq)2f4(x)=∑Dj=1[x2j-10cos(2πxj)+10]f5(x)=14000∑Dj=1x2j-∏Dj=1(xjj)+1f6(x)=418.9829∗D-∑Dj=1xjsin|xj|f7(x)=max{|xj|,1≤j≤D}f8(x)=∑Dj=1(⌊xj+0.5」)2f9(x)=∑Dj=1|xjsinxj+0.1×xj|f10 (x)= ∑Dj=1jx2jf11 (x)= ∑D-1j=1[100(xj+1 -x21)2 +(1-xj)2]f12(x)=∑Dj=1|xj|(j+1)f13 (x)= -20exp(-0.2∑Dj=1x2jD)-exp(∑Dj=1cos(2πxj)D)+ 20+ef14 (x)= ∑Dj=1x2j +(∑Dj=10.5jxj)2 +(∑Dj=10.5jxj)4f15 (x)= ∑Dj=1jx4jf16 (x)= -∑D-1j=1[exp(-(x2j+x2j+1 +0.5xjxj+1 )8)×cos(4x2j+x2j+1 +0.5xjxj+1 )]f17 (x)= 1-cos(2π‖x‖)+ 0.1‖x‖,‖x‖=∑Dj=1x2jf18 (x)= ∑Dj=1(106)j-1D-1x2jf19 (x)= ∑Dj=1(0.5+sin2(x2j+x2j+1 )-0.5(1+0.001(x2j+x2j+1 ))2),xD+1 =x1 表2 5种算法的仿真结果 函数算法20维50维100维平均值标准差平均值标准差平均值标准差f1DE3.87E-232.78E-23-1.33E-076.17E-08-3.89E-021.90E-02-HSDE1.61E-716.90E-71=7.40E-729.79E-72-6.51E-721.29E-71-RMDE1.37E-565.70E-56=1.07E-045.68E-04=2.64E-011.06E+00=SPS_DE/rand/12.01E-311.22E-31-1.14E-083.07E-09-2.69E+003.51E-01-CDMDE2.00E-2660.00E+002.50E-2510.00E+009.97E-2430.00E+00f2DE1.53E-119.46E-12-2.23E-032.63E-03-3.19E+002.64E+00-HSDE6.18E-365.61E-36-5.99E-363.08E-36-8.38E-368.65E-36-RMDE3.08E-151.38E-14=3.75E-021.35E-01=1.64E-012.12E-01-SPS_DE/rand/17.65E-192.56E-19-8.32E-069.49E-07-7.54E-015.03E-02-CDMDE3.95E-1421.02E-1415.76E-1302.55E-1291.09E-1265.26E-126f3DE5.13E-073.13E-07-2.30E+035.41E+02-1.20E+052.39E+04-HSDE2.99E-213.74E-21-1.12E-201.95E-20-5.72E-219.13E-21-RMDE1.31E-223.13E-22-7.99E+001.84E+01-3.85E+033.60E+03-SPS_DE/rand/16.53E-013.25E-01-3.87E+041.15E+04-2.96E+053.67E+04-CDMDE1.51E-1980.00E+003.62E-1611.32E-1601.59E-1338.72E-133f4DE8.77E+019.07E+00-3.63E+021.15E+01-8.36E+022.43E+01-HSDE6.12E+001.35E+00-6.03E+001.58E+00-6.57E+001.54E+00=RMDE4.20E-151.05E-14=3.32E-021.82E-01=1.47E-014.52E-01=SPS_DE/rand/19.41E-153.57E-14=1.16E+021.30E+01-5.52E+022.74E+01-CDMDE4.94E-032.71E-021.55E+006.01E+005.63E+001.74E+01f5DE1.73E-033.55E-03-2.23E-071.48E-07-2.30E-021.15E-02-HSDE5.34E-037.57E-03-5.42E-037.95E-03-3.04E-035.55E-03-RMDE2.23E-022.80E-02-4.56E-029.21E-02-5.77E-028.71E-02-SPS_DE/rand/10.00E+000.00E+00=1.84E-087.25E-09-8.53E-014.11E-02-CDMDE5.52E-063.03E-050.00E+000.00E+000.00E+000.00E+00f6DE2.95E+033.97E+02-1.25E+049.32E+02-2.97E+041.71E+03-HSDE1.09E+013.12E+01=1.50E+014.03E+01+1.58E+015.14E+01+RMDE2.55E-041.36E-12=9.02E-041.29E-03+1.79E-013.26E-01+SPS_DE/rand/17.90E+003.00E+01=1.41E+036.15E+02-1.99E+047.03E+02-CDMDE2.95E+008.60E+001.65E+023.38E+025.18E+029.45E+02f7DE2.37E-063.35E-06-7.98E+003.16E+00-9.42E+011.35E+00-HSDE5.92E-137.28E-13-6.13E-137.00E-13-4.93E-137.56E-13-RMDE3.21E-024.64E-02-2.47E-011.04E-01-3.56E-011.62E-01-SPS_DE/rand/11.52E-052.88E-06-5.16E+005.37E-01-3.99E+011.45E+00-CDMDE9.89E-1224.07E-1214.27E-1131.32E-1123.37E-1101.06E-109f8DE5.13E+021.21E+02-1.54E+043.18E+03-5.97E+048.91E+03-HSDE6.67E-022.54E-01=0.00E+000.00E+00=3.33E-021.83E-01=RMDE4.17E+006.22E+00-5.14E+017.34E+01-1.47E+022.00E+02-SPS_DE/rand/11.45E+022.33E+01-1.42E+041.59E+03-1.03E+056.96E+03-CDMDE0.00E+000.00E+000.00E+000.00E+000.00E+000.00E+00f9DE8.94E-032.98E-03-4.71E-028.16E-03-9.65E-021.32E-02-HSDE2.45E-057.35E-05+6.16E-051.27E-04=5.27E-059.78E-05=RMDE5.21E-131.87E-12+1.05E-031.46E-03=1.03E-021.12E-02-SPS_DE/rand/12.18E-051.69E-05+3.32E-022.40E-03-3.11E+001.38E+00-CDMDE1.11E-032.00E-034.65E-042.54E-034.44E-042.43E-03f10DE1.06E-248.40E-25-9.81E-093.97E-09-3.51E-031.48E-03-HSDE1.70E-734.02E-73-1.22E-731.41E-73-1.54E-733.69E-73-RMDE3.20E-588.51E-58-1.74E-069.45E-06=6.33E-039.14E-03-SPS_DE/rand/14.63E-333.03E-33-5.35E-101.47E-10-2.51E-013.47E-02-CDMDE8.37E-2690.00E+001.40E-2530.00E+001.15E-2430.00E+00 续表 函数算法20维50维100维平均值标准差平均值标准差平均值标准差f11DE1.64E-012.12E-01=4.09E+019.96E-01-9.81E+019.71E+00-HSDE3.99E-011.22E+00=1.33E-017.28E-01+3.99E-011.22E+00+RMDE5.11E-142.07E-13+1.77E+012.04E+01=7.20E+014.05E+01-SPS_DE/rand/11.42E+012.88E-01-4.49E+012.39E-01-1.02E+021.39E+00-CDMDE5.12E-011.13E+009.75E+001.56E+012.69E+013.45E+01f12DE3.30E-661.49E-65=1.82E-179.97E-17=1.21E-013.67E-01=HSDE6.16E-1112.30E-110=1.02E-1113.12E-111=3.08E-1121.55E-111=RMDE4.69E-1021.48E-101=3.41E-311.42E-30=1.23E-166.72E-16=SPS_DE/rand/16.99E-861.15E-85-5.97E-317.32E-31-9.74E-147.28E-14-CDMDE2.93E-2400.00E+000.00E+000.00E+000.00E+000.00E+00f13DE2.43E-128.94E-13-8.25E-051.90E-05-4.42E-022.33E-02-HSDE7.52E-151.23E-15-7.64E-151.95E-15-7.76E-159.01E-16-RMDE1.93E-101.05E-09=2.96E-021.60E-01=4.36E-029.21E-02-SPS_DE/rand/14.44E-150.00E+00-2.18E-052.90E-06-4.98E-015.84E-02-CDMDE8.88E-160.00E+008.88E-160.00E+008.88E-160.00E+00f14DE6.20E-094.63E-09-1.99E+024.16E+01-1.11E+031.32E+02-HSDE1.61E-241.75E-24-1.66E-242.07E-24-2.92E-245.21E-24-RMDE7.31E-341.84E-33-2.63E-036.98E-03-2.01E+022.08E+02-SPS_DE/rand/12.42E-031.04E-03-2.49E+021.68E+01-1.42E+038.23E+01-CDMDE2.82E-1860.00E+005.93E-933.12E-924.53E-491.57E-48f15DE3.89E-459.39E-45-4.57E-161.97E-15=1.00E-061.09E-06-HSDE1.58E-1294.67E-129=1.06E-1293.15E-129=1.03E-1294.92E-129=RMDE1.37E-916.35E-91=4.34E-172.14E-16=1.18E-094.90E-09=SPS_DE/rand/15.45E-566.47E-56-3.50E-161.52E-16-9.77E-042.58E-04-CDMDE0.00E+000.00E+000.00E+000.00E+000.00E+000.00E+00f16DE-7.35E+005.52E-01--9.66E+006.83E-01--1.26E+019.70E-01-HSDE-1.46E+013.98E-01--1.46E+013.00E-01--1.46E+013.49E-01-RMDE-1.90E+018.05E-15=-4.90E+011.96E-05=-9.90E+017.89E-03-SPS_DE/rand/1-1.84E+018.65E-01--2.75E+012.80E+00--2.63E+011.69E+00-CDMDE-1.90E+010.00E+00-4.90E+010.00E+00-9.90E+010.00E+00f17DE1.51E-014.75E-02-3.98E-014.35E-02-1.55E+001.36E-01-HSDE1.07E-012.54E-02-1.10E-013.05E-02=1.10E-013.05E-02=RMDE1.87E-019.73E-02-2.90E-011.75E-01-3.10E-011.75E-01-SPS_DE/rand/11.27E-014.50E-02-3.27E-014.13E-02-2.48E+001.04E-01-CDMDE9.16E-022.56E-029.99E-024.02E-099.99E-022.62E-09f18DE2.69E-202.87E-20-2.29E-042.03E-04-1.26E+026.24E+01-HSDE7.39E-681.14E-67-2.59E-713.45E-71-5.26E-687.66E-68-RMDE4.24E-422.32E-41=5.86E+013.18E+02=5.19E+031.62E+04=SPS_DE/rand/13.78E-282.53E-28-8.90E-062.21E-06-1.13E+031.16E+02-CDMDE6.78E-2660.00E+003.27E-2470.00E+008.97E-2410.00E+00f19DE2.45E-028.26E-03-7.32E-011.60E-01-2.88E+003.41E-01-HSDE1.07E-054.50E-06-1.33E-057.02E-06-1.05E-054.26E-06-RMDE7.24E-071.24E-06-7.77E-041.44E-03-2.32E-032.80E-03-SPS_DE/rand/17.10E-031.70E-03-6.87E-014.21E-02-4.97E+003.66E-01-CDMDE0.00E+000.00E+000.00E+000.00E+000.00E+000.00E+00 综上所述,CDMDE算法对大多数函数具有较强的全局寻优能力,较好的稳定性,但该算法对函数f4、f6、f9和f11优化性能不佳.造成CDMDE算法对少数函数表现不佳的原因是CDMDE算法中引入了一些局部参数,而这些局部参数取值主要依靠经验得出,这就使得该算法的通用性在一定程度上下降.未来的工作是加强参数设置的理论研究和提高算法的通用性. 为了直观显示CDMDE算法的优越性,这里选择了3种收敛曲线如图3、图4和图5,横坐标表示进化代数,纵坐标表示平均函数值. 表3 不同评价指标下的仿真结果汇总 算法20维NOBMNOBSTD+/-/=50维NOBMNOBSTD+/-/=100维NOBMNOBSTD+/-/=DE000/17/2000/17/2000/18/1HSDE011/12/6222/12/5222/11/6RMDE542/8/9321/7/11321/13/5SPS_DE/rand/1111/15/3000/19/0000/19/0CDMDE141315151515 从3种收敛曲线可以看出,CDMDE算法在进化前期就表现很好的收敛速度并且随着进化的进行CDMDE算法搜索到的平均值远小于其他算法,说明CDMDE算法具有较高的收敛精度. 图3 20维函数f1Fig.3 Function f1 for D=20 图4 50维函数f3Fig.4 Function f3 for D=50 图5 100维函数f18Fig.5 Function f18 for D=100 扰动作为一种避免种群陷入局部最优的手段,受到广大学者的青睐.扰动的形式是多种多样的,有基于rand函数的随机扰动[14]和小概率扰动[15]等.CDMDE算法融入了柯西扰动和小概率扰动,因此为了说明柯西扰动和小概率扰动对算法性能的影响,这里使用CDMDE算法的结构将融入柯西扰动的改进差分进化算法与无柯西扰动的CDMDE算法(NCDMDE)、rand随机扰动代替柯西扰动的CDMDE算法(RDMDE)和无小概率扰动的CDMDE算法(NSPDMDE)进行比较研究.比较结果如表4所示,其中加粗字体表示该算法的平均值或标准差不劣于其他算法. 表4 扰动的作用 函数NCDMDERDMDENSPDMDECDMDE平均值标准差平均值标准差平均值标准差平均值标准差f11.15E-023.38E-022.87E-1640.00E+001.36E-2530.00E+002.00E-2660.00E+00f22.65E-024.51E-024.75E-891.24E-882.07E-1364.70E-1363.95E-1421.02E-141f38.40E+003.08E+012.72E-1607.30E-1601.81E-1980.00E+001.51E-1980.00E+00f42.68E-011.42E+001.07E+003.82E+003.41E-011.19E+004.94E-032.71E-02f51.13E-012.04E-012.54E-035.76E-030.00E+000.00E+005.52E-063.03E-05f61.25E-012.82E-015.74E+001.32E+014.09E+031.09E+032.95E+008.60E+00f71.15E-019.64E-029.97E-792.25E-782.66E-1189.60E-1189.89E-1224.07E-121f89.10E+007.10E+000.00E+000.00E+000.00E+000.00E+000.00E+000.00E+00f91.68E-035.69E-032.71E-032.00E-032.06E-045.32E-041.11E-032.00E-03f101.39E-035.68E-031.68E-1670.00E+002.26E-2540.00E+008.37E-2690.00E+00f114.35E-041.06E-038.87E-013.15E+001.60E+018.31E-025.12E-011.13E+00f127.31E-143.37E-133.37E-2090.00E+001.01E-2430.00E+002.93E-2400.00E+00f134.08E-028.80E-028.88E-160.00E+008.88E-160.00E+008.88E-160.00E+00f144.26E-011.25E+008.45E-1582.47E-1573.88E-1860.00E+002.82E-1860.00E+00f152.67E-105.85E-102.30E-3200.00E+000.00E+000.00E+000.00E+000.00E+00f16-1.90E+012.37E-03-1.90E+010.00E+00-1.90E+010.00E+00-1.90E+010.00E+00f172.15E-011.16E-019.99E-023.02E-109.75E-021.29E-029.16E-022.56E-02f186.80E+032.08E+047.15E-1660.00E+003.57E-2530.00E+006.78E-2660.00E+00f192.31E-043.58E-047.08E-151.03E-140.00E+000.00E+000.00E+000.00E+00 从表4可以看出,CDMDE算法性能明显优于其他算法.就平均值而言,NCDMDE算法、RDMDE算法、NSPDMDE算法和CDMDE算法在所有算法中表现最优的函数个数分别为3、3、8和14;就标准差而言,NCDMDE算法、RDMDE算法、NSPDMDE算法和CDMDE算法在所有算法中表现最优的函数个数分别为2、9、13和14,另外,RDMDE算法、NSPDMDE算法和CDMDE算法优化很多函数的标准差都为0.因此,CDMDE算法表现最优,NSPDMDE算法的性能仅次于CDMDE算法并且就标准差而言NSPDMDE算法的性能略低于CDMDE算法.综上分析,柯西扰动对算法性能的提升非常明显,提高了算法的全局寻优能力,在CDMDE算法中的小概率扰动也一定程度上提高算法的稳定性和收敛精度,但作用低于柯西扰动,若在CDMDE算法中无柯西扰动,则算法表现最差.此外,RDMDE算法中的rand随机扰动明显没有柯西扰动对算法性能提升好,但比NCDMDE算法性能要好.因此,就提升算法性能而言,柯西扰动比小概率扰动和rand随机扰动好,rand随机扰动比无柯西扰动的算法好. 最优个体信息复制和改进的交叉策略是CDMDE算法中的两种改进措施,为了分析他们各自在CDMDE算法中所起的作用,这里使用CDMDE算法的结构将无最优个体信息复制的CDMDE算法(NCBEST)、无交叉策略改进的CDMDE算法(NMCDE)与CDMDE算法进行对比分析.他们的性能优劣通过平均值、标准差和改进率μk=mk/(m3+δ)(k=1,2)得出,结果如表5所示.m1、m2和m3分别表示NCBEST、NMCDE和CDMDE算法的平均值.δ为足够小的正数,该值是为了防止分母为0.μk表示两个比较算法分别与CDMDE算法的比值,若μk大于等于1,则表示对某函数CDMDE算法不劣于比较算法,μk越大,说明新算法的改进机制越有效;反之,若μk小于1,则表示对某函数CDMDE算法劣于比较算法.其中加粗字体表示该算法的平均值或标准差不劣于其他算法.另外,对μ1和μ2中大于等于1的数也进行了加粗. 从表5可以看出,CDMDE算法优于其他两种算法.在平均值方面,与其他算法相比CDMDE算法对14个函数表现最优,而NCBEST算法和NMCDE算法在三种算法中表现最好的函数个数分别为9和5;就标准差而言,NCBEST算法、NMCDE算法和CDMDE算法表现最优的函数个数分别为13、8和15,对于这三种算法优化很多函数的标准差都为0,说明三种算法的稳定性都较好;在改进率方面,对大多数函数NCBEST和NMCDE的改进率都大于等于1,且NMCDE的改进率大于NCBEST,因此,最优个体信息复制和改进交叉策略能提升算法的全局寻优能力,交叉策略的改进对算法性能的提升更大. 表5 最优个体信息复制和改进交叉策略的作用 函数NCBEST平均值标准差μ1NMCDE平均值标准差μ2CDMDE平均值标准差f17.18E-2640.00E+003.59E+022.08E-1333.17E-1331.04E+1332.00E-2660.00E+00f27.38E-1403.16E-1391.87E+025.78E-704.78E-701.46E+723.95E-1421.02E-141f31.69E-1970.00E+001.12E+011.24E-714.42E-718.21E+1261.51E-1980.00E+00f46.32E-023.39E-011.28E+011.98E-015.09E-014.01E+014.94E-032.71E-02f50.00E+000.00E+0000.00E+000.00E+0005.52E-063.03E-05f61.46E+016.84E+014.95E+002.15E+012.93E+017.29E+002.95E+008.60E+00f71.93E-1207.37E-1201.95E+013.40E-318.36E-313.44E+909.89E-1224.07E-121f80.00E+000.00E+0010.00E+000.00E+0010.00E+000.00E+00f94.30E-041.19E-033.87E-011.15E-031.29E-031.04E+001.11E-032.00E-03f101.21E-2630.00E+001.45E+053.39E-1357.22E-1354.05E+1338.37E-2690.00E+00f114.04E-017.11E-017.89E-012.64E-013.44E-015.16E-015.12E-011.13E+00f120.00E+000.00E+0009.61E-2620.00E+003.28E-222.93E-2400.00E+00f138.88E-160.00E+0018.88E-160.00E+0018.88E-160.00E+00f141.22E-1850.00E+004.33E+006.56E-651.25E-642.33E+1212.82E-1860.00E+00f150.00E+000.00E+0012.45E-2590.00E+0010.00E+000.00E+00f16-1.90E+010.00E+001-1.90E+010.00E+001-1.90E+010.00E+00f178.41E-023.17E-029.18E-019.99E-021.55E-101.09E+009.16E-022.56E-02f185.88E-2610.00E+008.67E+043.66E-1315.88E-1315.40E+1346.78E-2660.00E+00f190.00E+000.00E+0012.56E-101.26E-1010.00E+000.00E+00 为了进一步分析CDMDE算法中双策略变异算子(BSM)的作用,在该算法框架下,选择三种经典的变异算子(DE/rand/1,DE/current-to-best/1,DE/ best/1)作对比实验.基于平均值和标准差指标,将4种算子在每个函数上进行排名,最后将每种算子的总排名除以函数个数得到每个算子的平均排名,平均排名越低的算子性能越好,反之,平均排名越高的算子性能越差.4种算子的平均排名用柱状图6所示,每个柱形图上方的数字表示该算子平均排名. 从图6可以看出,不管对于平均值还是标准差,平均排名最低的算子为BSM,说明新算法中的变异算子平均优化性能和鲁棒性最好.DE/best/1算子对平均值和标准差而言平均排名都最高,造成这的原因是该算子易陷入局部最优.其他两种算子平均排名同样较高,介于BSM和DE/best/1算子之间.因此,单一变异策略无法适应算法搜索的不同阶段,算法进化过程中前期要求保证种群多样性,尽可能的遍历搜索空间,避免出现早熟收敛;后期希望算法更精确的搜索,加快搜索速度.双策略变异中DE/rand/1策略可以适应算法前期搜索,DE/current-to-best/1策略可以满足算法后期搜索,两种策略在不同搜索阶段所占的比重动态调节.因此,双策略变异的CDMDE算法显示出了优良的性能. 图6 4种算子平均排名Fig.6 Average ranking of four mutation operators 利用CDMDE算法对3机组和38机组进行30次独立实验.其中,CDMDE算法优化两个算例的种群规模和z值分别为40和1,且他们的最大进化代数分别为300和3000,惩罚系数为1020,其余参数不变.解的可行性往往比目标函数值更重要,因此将30次独立实验的最优值和对应的约束违反量与其他文献进行比较.对于3机组,经过30次独立实验CDMDE算法的最优解P=(393.170569,334.602777,122.226654),最优解的目标函数值为8194.356121,该目标函数值与文献[21]中的目标函数值相同,并且CDMDE算法和文献[21]中的约束违反量都为0,说明他们对该算例的优化性能相同.对于38机组,CDMDE算法与其他文献方法对比见表6.30次独立实验中CDMDE算法的最优解P=从表6看出,CDMDE算法优化38机组得到的最优值为9417331.431253,且满足系统所有的运行约束.而其他5种方法得到的最优目标函数值均比CDMDE算法大,且这5种方法的约束违反量都不为0,说明他们无法有效找到可行解.因此,CDMDE算法可以优化出既满足系统各种运行约束的情况下,又使发电成本最小的较优解. 表6 不同方法优化38机组电力系统经济调度问题的对比 方法最优值违反量 SPSO[25] 9543984.7770.004 PSO_Crazy[25] 9520024.6010.005 New PSO[25] 9516448.3120.003 PSO_TVAC[25] 9500448.3070.005 λ-logic[22] 9447031.77549.1569 CDMDE 9417331.4312530 (420.897283,434.647261,426.694397,428.853213,432.403767,430.862396,428.264389,433.406684,114.00642,114.012771,122.405587,127.570354,110.000346,90,82.000328,120.000478,158.691548,65.000941,65.000046,271.938996,271.94118,259.968287,129.885306,10,111.386999,87.187023,35.517238,20.000265,20.000039,20.0002,20,20.00043,25.00012,18.000414,8.000026,25.000067,20.665701,20.7894 9899999952). 针对差分进化算法提早收敛等缺点,提出了融入柯西扰动的改进差分进化算法.新算法在变异策略中采用双策略变异和柯西扰动,有效平衡了全局搜索和局部搜索.中心解和最优解联合去改进交叉策略中解的选取.自适应参数保留了优秀参数,劣质参数则被重新生成.小概率扰动和最优个体信息复制机制进一步加强了算法收敛到全局最优解的能力.采用了19个测试函数和2个电力系统经济调度问题比较CDMDE算法、其他DE算法和文献中的方法,实验结果证明了CDMDE算法具有更高的收敛精度.3.3 交叉策略的改进
3.4 最优个体信息复制机制

3.5 自适应调整参数
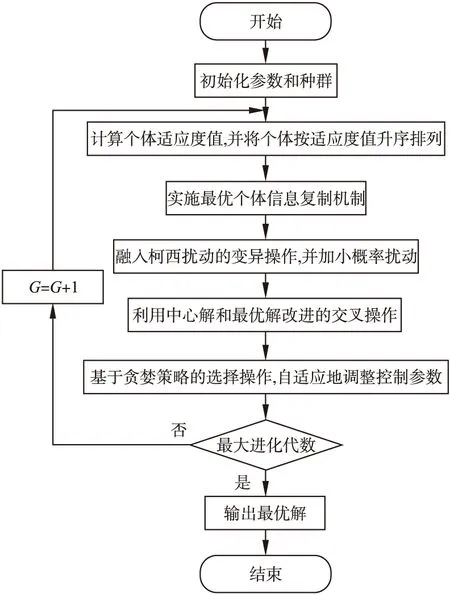
3.6 算法实现流程图
4 电力系统经济调度优化
4.1 目标函数
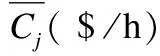
4.2 约束处理

5 算法性能测试
5.1 函数测试结果对比分析
Table 1 19 test functions
Table 2 Simulation results of five algorithms
Table 3 Summary of simulation results under different evaluation indicators

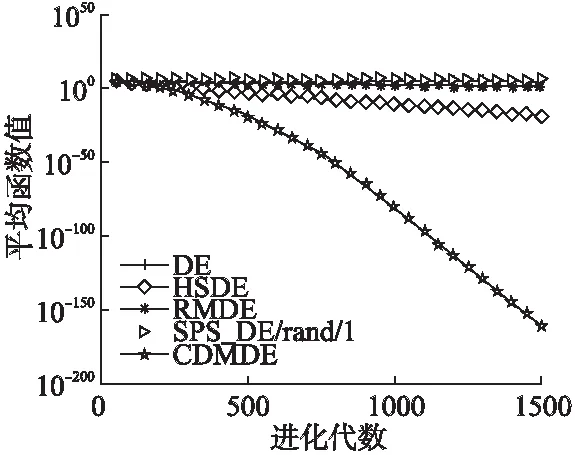

5.2 扰动作用分析
Table 4 Effect of the disturbance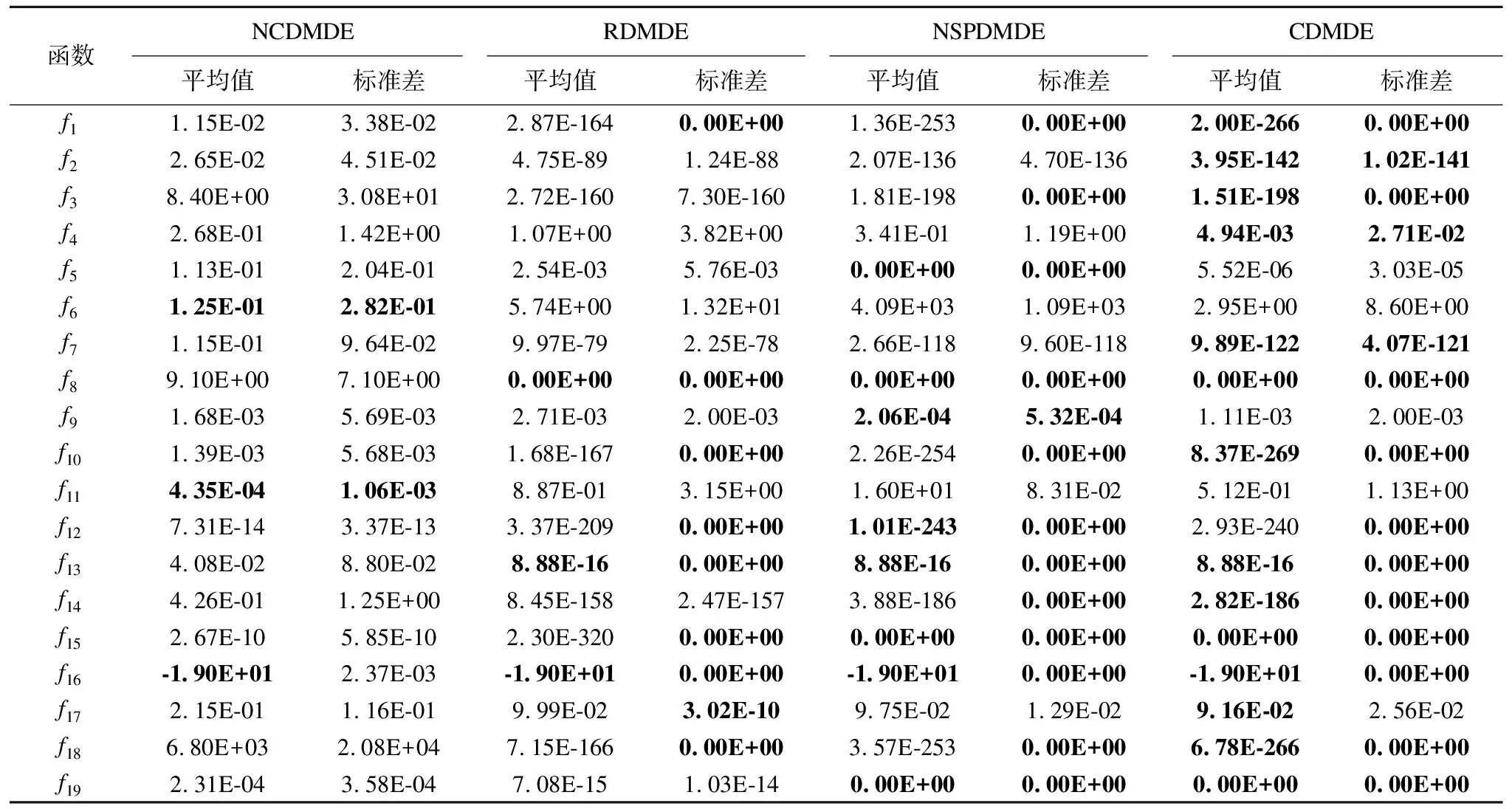
5.3 最优个体信息复制和改进交叉策略分析
Table 5 Effect of the optimal individual information replication and modified crossover strategy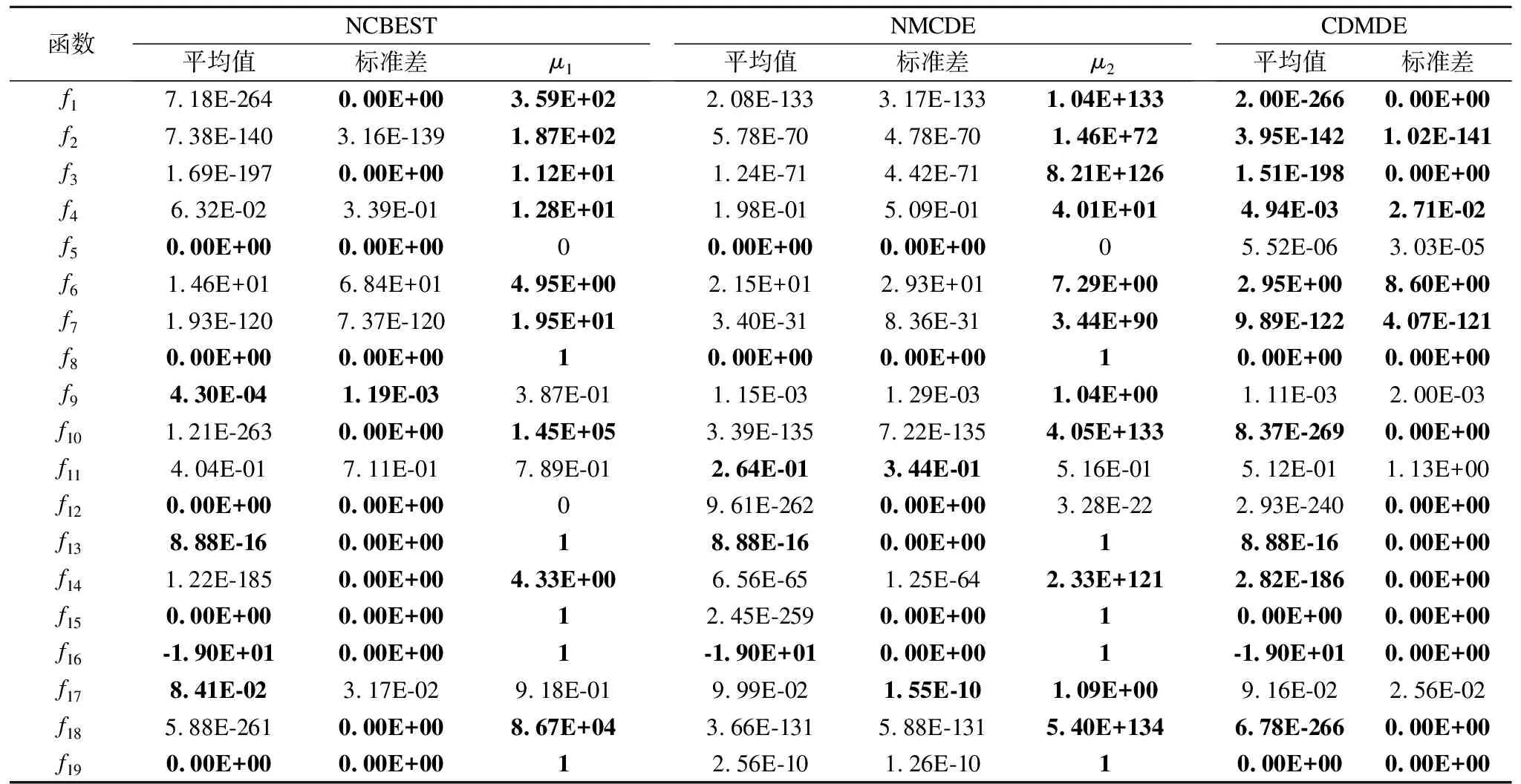
5.4 算子性能分析
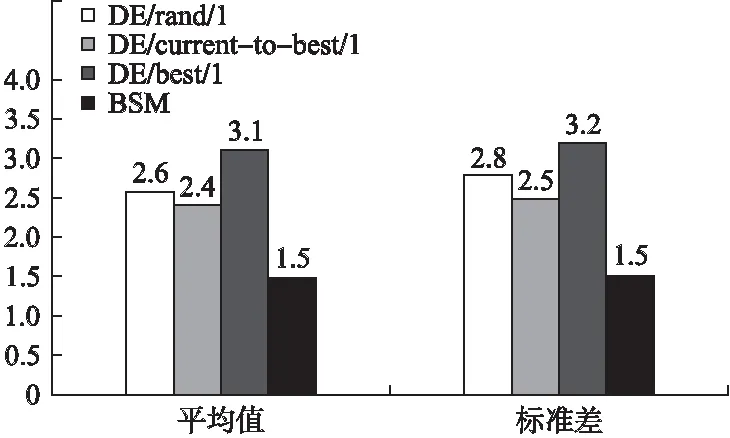
5.5 电力系统经济调度问题优化结果与分析
Table 6 Comparison among different approaches for 38-unit economic load dispatch problem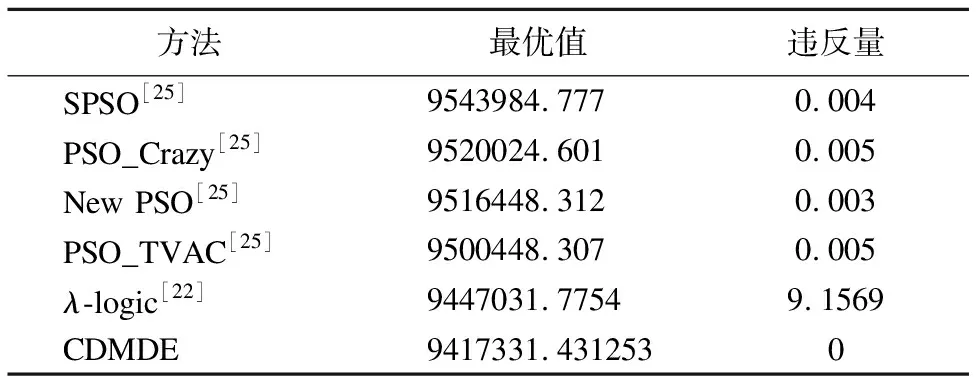
6 结束语
