基于Sponge结构的轻量级Hash函数设计

赵太飞，尹 航，李永明

(西安理工大学 自动化与信息工程学院，西安 710048)

1 引 言

随着物联网技术(Internet of Things，IOT)的高速发展，其存在的安全隐私问题也越来越受到人们重视.Hash函数是应对安全威胁的有效手段，同时也是密码学的重要组成部分，它可以将任意长的消息映射成为固定长度的消息摘要，是一种单向散列函数.主要应用于数字签名、射频识别技术(Radio Frequency Identification，RFID)、随机数生成、鉴定消息的完整性和准确性等方面.针对RFID系统、无线传感器网络(Wireless Sensor Network，WSN)等场景，安全性不再是衡量算法的唯一标准.因为在这些资源受限条件下，硬件只有有限的计算能力和很小的存储空间.这就要求用于信息安全的加密算法必须“轻量化”：在保证一定安全性的前提下有较小的实现代价，占用较低的硬件资源，有很快的处理速度[1].文献[2]中提到在RFID系统中用于安全加密的标准门电路(Gate Equivalent，GE)可能只有200～2000个，很显然传统的Hash函数并不能满足这一点.Tianyong Ao等人于2014年提出的国家商密标准Hash函数SM3 的最优化硬件实现仍需6904 GE[3].

从针对资源受限环境的Hash函数概念提出到现在，国内外学者设计了一系列轻量级Hash函数：SQUASH[4]、PHONTON[5]、Quark[6]、SPONGENT[7]、Lesamnta-LW[8]、GLUON[9]、DM-PRESENT[10]、LHash[11]等.但由于目前没有统一的轻量级Hash函数标准，这些算法针对硬件效率，或针对软件效率各有侧重.本文设计了一种轻量级Hash函数，在满足一定安全性的同时具有较好的软硬件实现效率.

2 Sponge结构和Klein算法

2.1 Sponge结构

在设计构造Hash函数时，根据不同的迭代结构和压缩函数有不同的实现方法.目前常用的迭代结构有：DM结构、MD(Merkle-Damgård)结构、Sponge结构等.基于置换函数的Hash函数可采用Sponge结构，如作为SHA-3标准算法的Keccak算法[12]，该算法可通过参数调节进行轻量化实现.相较于其它结构，Sponge 结构对随机预言机区分攻击具有可证明安全性[13]，且没有前向反馈，实现起来只需要较小内存和硬件开销，更适合于轻量级Hash函数的设计.

一个典型的Sponge结构如图1所示，其中Mt为填充后的消息分组，Hs为压缩后的消息摘要分组，f(•)为压缩函数，r是输入消息分组长度，c为容量.加密流程为：待处理的消息通过填充处理后分为r位一组.第一组M0与初始r位数据异或后与初始c位数据拼接通过压缩函数f(•)，输出的中间状态前r位与M1异或后与中间状态剩下的c位数据拼接作为下一轮输入，依次重复直到所有消息吸收完毕.压缩阶段将压缩函数f(•)输出的中间状态作为下一轮的输入，并提取H0，H1，…，Hs各子串连接起来成为消息摘要.

图1 Sponge结构图Fig.1 Sponge structure

2.2 Klein算法

针对RFID系统和无线传感网络等资源受限环境，Gong等人在 RFIDSec 2011 会议上提出了一种基于SP(Substitution-Permutation Network)结构的轻量级分组加密算法Klein.算法轮加密如图2所示：明文P分组后与每一轮的轮密钥进行异或操作，产生的中间状态通过16个4比特S盒，再进行左移操作RotateNibbles，然后进行线性置换MixNibbles，依次进行n轮迭代最终产生密文C.

图2 Klein轮加密Fig.2 Round transformation of KLEIN

Klein算法的分组长度为64bit，密钥长度为可变的64、80或96bit，可以定义为Klein-64/80/96，与之对应的加密轮数为12、16或20轮.该算法主要关注资源受限环境下的软件实现，特别是在较低硬件资源下如8位处理器平台上.算法设计者声称：Klein-80/96有很好的安全性可以应对大多数的应用场景，而Klein-64有很好的软硬件实现性能可用于Hash函数设计以及消息认证[14].

3 Hash函数构造与实现

3.1 Hash函数设计

3.1.1 参数设置及预处理

本文采用的迭代结构为Sponge结构，算法整体结构如图3所示.消息经过预处理后分为M0到Ms一共s个分组，经过s次压缩函数F的处理后完成吸收操作.然后再通过n次压缩函数F的处理且每次提取一个子串，从H0到Hn一共n+1个子串拼接成摘要.压缩函数的每轮运算主要由轮密钥加，Substitution层，RotateNibbles，Permutation层组成.

图3 Hash函数算法结构Fig.3 Hash function algorithm structure

考虑到轻量化需求，具体设计时取吞吐率r=8bit，容量c=56bit，那么置换长度b=64bit.消息摘要长度为64bit，拥有64bit的内存状态.加密前的预处理操作为：将内存状态的初始值设为0，输入消息转换为二进制后进行填充.在消息后面填充一个1，然后填充若干个0，使之长度为r的最小整数倍.例如当消息长度length 对r取余值为1时，填充的值为“100000000”. 再对填充后的数据进行吸收、压缩运算.

3.1.2 压缩函数设计

预处理后的消息要通过压缩函数的处理完成吸收，压缩函数的设计借鉴了Klein算法的思想，并对其进行优化，使之更契合“轻量化”的设计目标.主流程可描述为：

fori= 1 toNRdo

AddRoundKey(STATE，ski)；

Substitution(STATE)；

RotateNibbles(STATE)；

Permutation(STATE)；

ski+1=KeySchedule(ski，i)；

其中i表示轮数，STATE表示中间状态，ski表示轮密钥.每轮运算开始先将输入的中间状态与产生的轮密钥进行轮密钥加，也就是异或运算.轮密钥生成算法采用典型的Feistel结构[15]，将迭代轮数Nr作为变量参与运算.密钥更新流程如下所示，其中ski[n]表示第i轮密钥的第n个字节，⨁表示异或运算，sbox[•]表示用s盒(sbox)对数据进行非线性变换.

ski+1[0]=ski[5]；

ski+1[1]=ski[6]；

ski+1[2]=ski[7]⨁Nr；

ski+1[3]=ski[4]；

ski+1[4]=ski[1]⨁ski[5]；

ski+1[5]=sbox[ski[2]⨁ski[6]]；

ski+1[6]=sbox[ski[3]⨁ski[7]]；

ski+1[7]=ski[0]⨁ski[4]；

轮密钥加后的STATE通过Substitution层进行非线性置换，Substitution层采用16个并行相同的s盒，s盒为Klein中的4位s盒，可以将4位输入非线性变换为4位输出，如表1所示.

表1 4比特s盒Table 1 4-Bit S-box

RotateNibbles操作将通过Substitution层的数据左移16bit.然后通过Permutation层进行线性置换，依次迭代12轮完成压缩函数的运算.Permutation层没有采用Klein中的置换操作而是使用文献[15]中的位排列置换，这样可以有更好的硬件实现性能，置换表如表2所示.

表2 P置换表Table 2 P- permutation table

3.2 算法优化设计

本文设计的Hash函数主要针对的是资源受限环境，硬件条件多为8位处理器.为了在8位处理器环境下有较高效率，采用面向字节的思想对算法进行优化设计，将字节作为运算单位.对待加密的数据按字节读取，吸收和压缩阶段以及轮密钥加、轮密钥更新都是字节运算.Permutation层是位排列操作，硬件实现有较高的效率，但软件实现效率并不高.所以软件实现时并没有直接进行按位排序操作，而是对字节数据进行移位操作，并与按顺序移位的十六进制0x80进行与运算获得比特数据.Substitution层软件实现时将两个4bit输入输出的s盒拼接为8bit的输入输出s盒，并生成一个容量为256字节的表.通过面向字节的查表操作即可完成非线性变化，Substitution层中64bit中间状态的非线性变换只需要8次查表操作.例如输入字节为0x09，通过查表3可得输出为0x73.

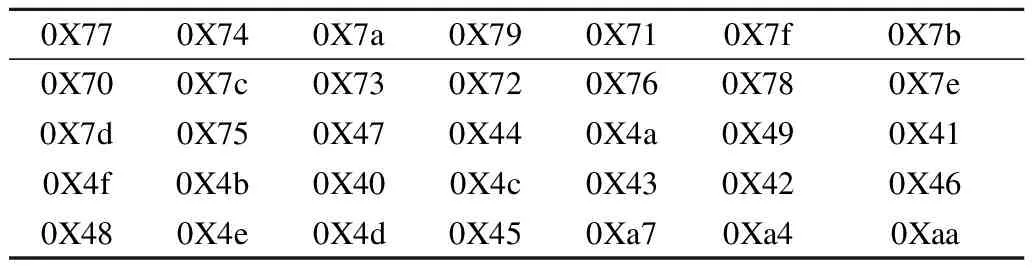
表3 非线性表(部分)Table 3 Non-linear table (part)

4 硬件和软件效率

4.1 硬件实现效率

本节用等效门电路GE个数来衡量算法的硬件实现规模.运算过程中需要用于存储64位中间状态的寄存器，大约需要384.8GE.密钥生成过程同样需要64位的寄存器，大约需要384.8GE，除此之外轮密钥的生成还需要一个8位的异或运算用于将轮数参与运算，大约需要21.8GE.吸收阶段需要8位异或运算用于吸收消息，大约需要21.8GE.压缩函数中：轮密钥加需要64位异或运算，大约需要174GE.Permutation层可通过硬件电路实现不需要门电路.Substitution层采用的是相同的s盒，可以采用一个4x4的s盒实现，大约需要28GE.轮密钥生成需要一个s盒，大约需要28GE，移位操作可通过改变布线逻辑实现，不需要门电路.综上，共需384.8+384.8+21.8+21.8+174+56=1041.6GE.与文献[16]总结的几种Hash函数硬件实现进行对比，如表4所示.

表4 硬件实现规模对比Table 4 Hardware implementation scale comparison

4.2 软件实现效率

在AMD AthlonII X2 250 3GHz，Windows7 32位平台下用C++对算法进行实现.并与同样采用Sponge结构作为SHA-3标准的经典Keccak算法进行对比.多次实验取均值，结果如表5所示.

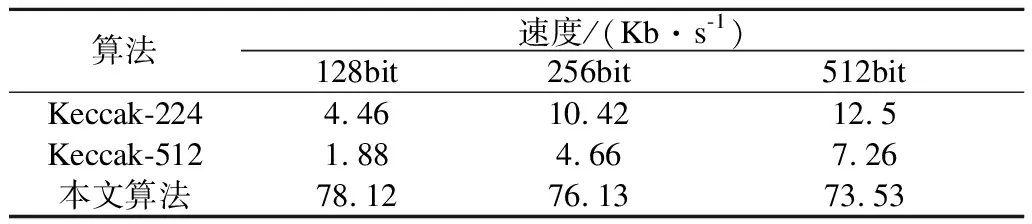
表5 软件效率对比Table 5 Software efficiency comparison

通过软硬件实现对比可以看出：本文算法的硬件实现GE数在2000GE之下，满足RFID等资源受限环境对硬件实现规模的要求；软件实现通过面向字节优化，相较于传统采用Sponge结构的Hash函数处理速度有了极大的提升，兼顾了软件效率.

5 安全性测试与分析

5.1 依赖性测试

依赖性测试就是通过统计学的方法对密码算法的混淆程度和扩散性给出一个概率上的结论，主要包括完备性，雪崩效应度da，严格雪崩准则dsa等.理想状态下，任何一位输入的改变都会引起半数输出值的改变；任何一位输入改变引起每位输出都以1/2的概率发生改变.

对64bit的数据进行10000次测试，从第二次开始，每次随机改变上次输入值的某一位，将得到的64bit输出值与上个输出值进行对比，得到测试数据如表6所示.可以看出输入改变一位输出改变位数的平均值接近32位，输入改变一位输出位改变的概率接近0.5.完备度为1，雪崩效应度和严格雪崩准则均接近1，有较好的依赖性.

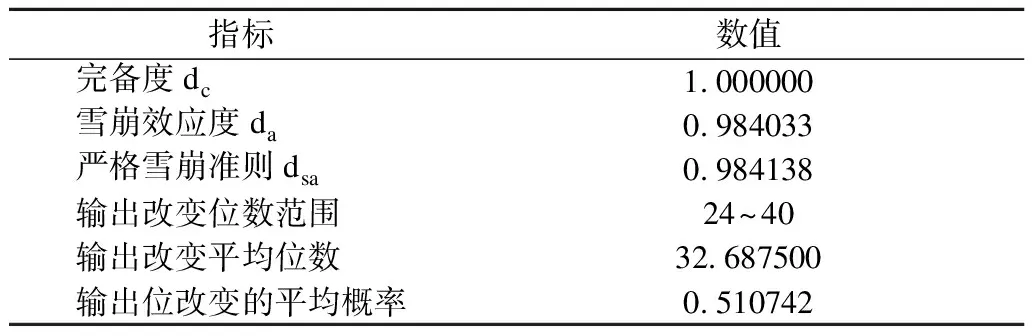
表6 依赖性测试结果Table 6 Dependency test

5.2 抗碰撞、原像和第二原像测试分析

理想情况下Hash函数是无碰撞的，但实际情况中很难做到这一点.本节对算法进行碰撞测试：随机取一组明文，测试n次，每次随机改变输入值的其中1bit，对改变前后输出值的ASCII码进行对比.若输出值相同位置的ASCII字符相同则称为碰撞一次，统计碰撞次数.多次试验取均值，测试次数n分别为2000、4000、8000、10000，测试结果如表7所示.可以看出4000次碰撞测试时，有94次碰撞1次，3906次没有发生碰撞，最大碰撞次数为1.当碰撞测试10000次时有270次碰撞1次，6次碰撞2次，9724次没有发生碰撞，最大碰撞次数为2，所以碰撞很小.

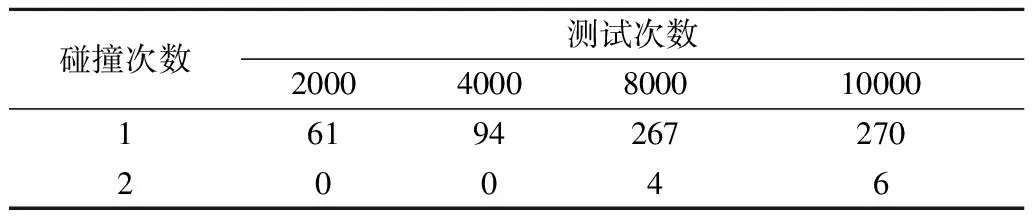
表7 碰撞测试结果Table 7 Collision test

同时对算法的抗碰撞、抗原像以及第二原像性能进行理论分析，由于对基于Sponge结构的Hash函数抗传统攻击的能力已有深刻研究，这里直接利用公式进行计算：

抗碰撞攻击：min{2n/2，2c/2}；

(1)

抗原像攻击：min{2n，2c，max{2n-r，2c/2}}；

(2)

抗第二原像攻击：min{2n，2c/2}.

(3)

其中n为输出位数，c为容量大小，r为输入消息分组长度.那么本文算法抗碰撞、原像和第二原像能力分别为：228，256，228.

5.3 滑动攻击分析

滑动攻击主要针对轮密钥的生成，受到了相关密钥攻击的启发，利用轮迭代函数的周期性，通过找到满足相关条件的明文-密文对，由他们之间的关系式获取密钥信息.本文采用的密钥调度算法基于Feistel结构，具有很好的非对称性.采用了一个轮计数器，将迭代轮数参与运算，利用s盒进行非线性置换.产生密钥的轮函数内有移位操作，且中间状态更新时也有适当移位操作.不具有自相似性，可以很好的抵抗滑动攻击.

5.4 差分和线性分析

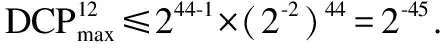
6 结 语

本文设计了一种轻量级Hash函数，迭代结构采用主流的Sponge结构，内部变换采用改进的Klein算法，非线性置换层是硬件实现效率较好的位排列，同时为了兼顾软件实现效率，对软件实现进行面向字节的优化.最后对算法进行依赖性实验和常规攻击分析，结果表明算法具有良好的扩散混淆性，并能抵抗常见攻击.效率测试表明算法的硬件实现所需门电路数大约为1042GE，且有较好的软件实现效率，适用于资源受限环境.