基于模态连续追踪的铁道车辆车体低频横向晃动现象研究
2019-01-18夏张辉周劲松孙文静
夏张辉, 周劲松, 宫 岛, 孙文静, 孙 煜
(同济大学铁道与城市轨道交通研究院, 上海 201804)
目前,客运专线上运营的铁道车辆偶尔出现不明原因的车体横向晃动加速度数据,图1为某次试验过程中检测到的铁道车辆车体横向晃动加速度数据,其特点为晃动频率低且持续时间短。由于车体横向晃动频率接近人体敏感频率区域,从而严重恶化了车辆的乘坐舒适性[1]。文献[2]研究了不同速度下四轴机车系统模态阻尼,发现当轮对蛇行运动频率接近车体固有振动频率时,车辆系统模态阻尼出现大于零的现象,此时车体横向振动不收敛。文献[3]通过结合线上试验,研究一系、二系悬挂参数对铁道车辆车体低频横向晃动的影响规律。文献[4]建立整车蛇行运动模型并分析了不同速度下车辆系统的特征根,发现当轮对蛇行运动频率接近车体模态频率时,车辆系统部分特征根位于正实部区域,导致车体出现剧烈低频横向晃动。以上文献均为铁道车辆车体低频横向晃动的研究提供了良好思路,由于出现车体低频横向晃动时轮对蛇行运动频率刚好接近车体模态频率,且此时车辆系统模态阻尼发生异常变化,因而,通常认为车体低频横向晃动是随着车辆运行速度的提高,轮对蛇行运动频率曲线“穿越”车体模态频率曲线时产生的共振失稳。然而,共振不会引起车辆系统模态阻尼的异常变化,并且在轮对蛇行运动频率曲线必然会“穿越”车体模态频率曲线的情况下,仅有部分铁道车辆会出现车体低频横向晃动现象。因此,铁道车辆车体低频横向晃动的机理仍不明确。
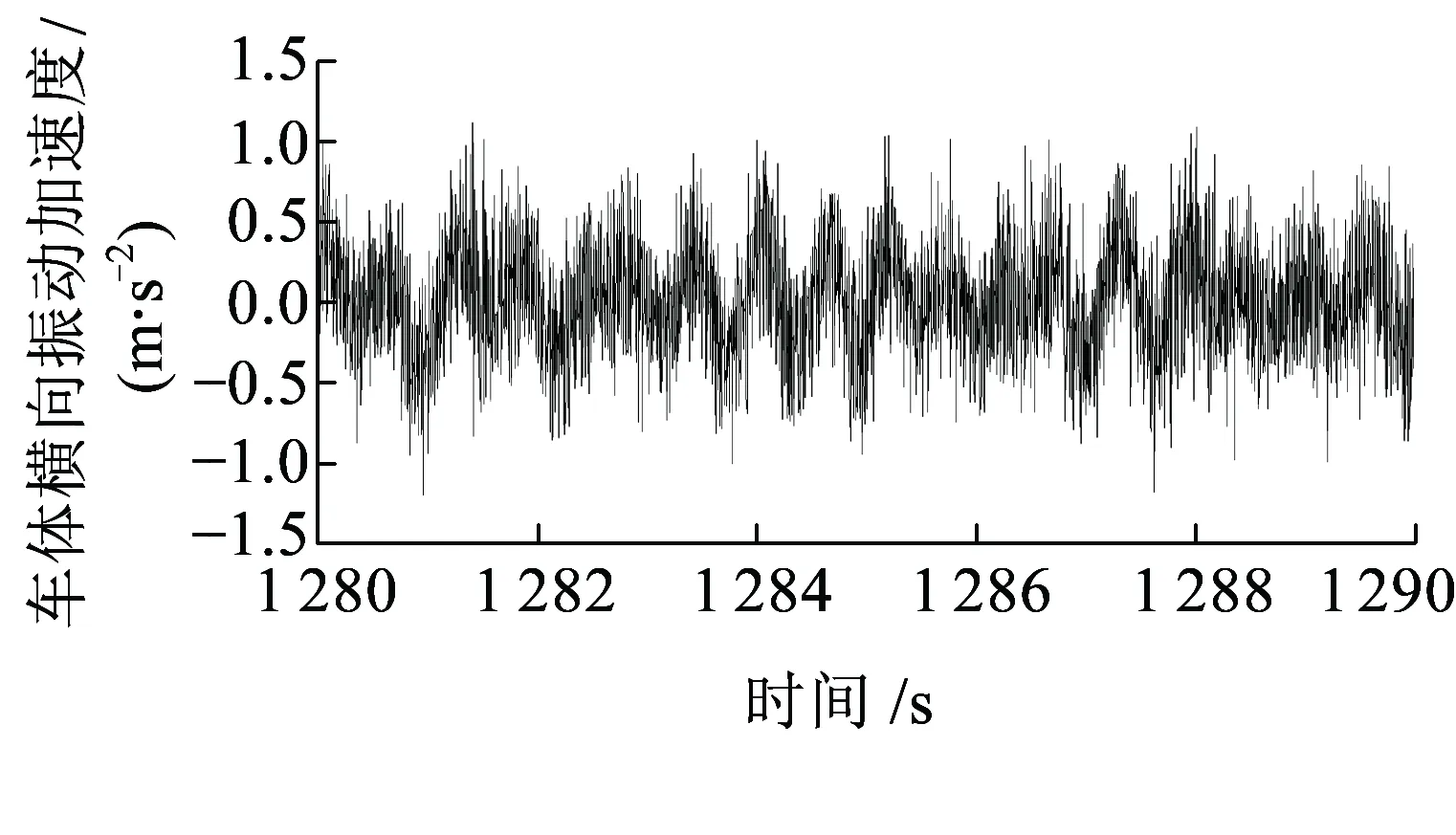
图1 车体低频横向晃动实测加速度数据
实际上,车辆系统整体是一个非保守自激振动系统[5],不同速度下车辆系统模态变化极为复杂。模态阻尼的异常变化实则为不同速度下的多模态耦合振动问题,速度通过影响轮轨接触阻尼,进而影响整个自激振动系统的耦合振动特征。在基础力学[6-7]和航空航天[8-9]研究领域,多体动力学系统在模态频率曲线接近时的多模态耦合振动问题已有较多研究,而在铁道车辆领域却鲜见此方面的研究。本文提出基于Lagrange三次样条插值连续追踪方法,基于该方法追踪不同速度下系统各阶模态变化规律,研究当轮对蛇行运动模态频率接近车体模态频率时,究竟是哪几阶模态阻尼发生了异常变化,并利用模态振型研究模态阻尼异常变化前后相应模态的耦合振动特征。据此揭示铁道车辆车体低频横向晃动的机理。基于该机理,研究车体低频横向晃动的指标判据,并对其有效性进行验证。本文研究结果可为铁道车辆车体低频横向晃动研究及治理提供参考。
1 车辆系统复模态分析
在对车辆系统进行模态分析之前,将一系、二系悬挂参数线性化,并采用线性轮轨接触关系[10]。由于轮轨接触部分具有一般黏性阻尼且数值较大,因此针对车辆系统的模态分析实际上是复模态分析。
当车辆运行速度为v,在无轨道随机不平顺作用下,轮对、转向架、整车线性振动微分方程可以表示为
式中:YL为系统的广义坐标列向量,阶数为n,由系统自由度数决定;M、C、K分别为悬挂系统质量、阻尼、刚度矩阵;CWR、KWR为与轮轨接触参数有关的矩阵。
将物理坐标方程( 1 )转化为状态坐标方程[11],有
( 2 )

设式( 2 )特解为YL′=φ′eτt,有
(τP+Q)·φ′=0
( 3 )

( 4 )
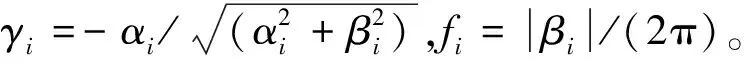
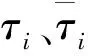

( 5 )

2 基于Lagrange三次样条插值的模态连续追踪
为详细了解车辆系统在不同速度下各阶模态的发展规律,还需解决不同速度下系统模态频率、模态阻尼及模态振型的归属问题,即实现不同速度下车辆系统模态的连续追踪,对研究车辆系统模态阻尼异常变化尤为关键。
由于模态频率、模态阻尼及模态振型总是同时出现的,实现其中一个的连续追踪,则可同时确定另外两个的归属问题。实际研究过程中发现,系统模态阻尼会出现2阶及2阶以上模态阻尼在某速度段内均相等的情况,这会导致模态连续追踪过程中的错误;系统模态振型向量的维度较高,数值计算难度较大;考虑到系统模态频率的连续性较好,在实际追踪过程中的鲁棒性较高,因此,本文采取模态频率的连续追踪方法。
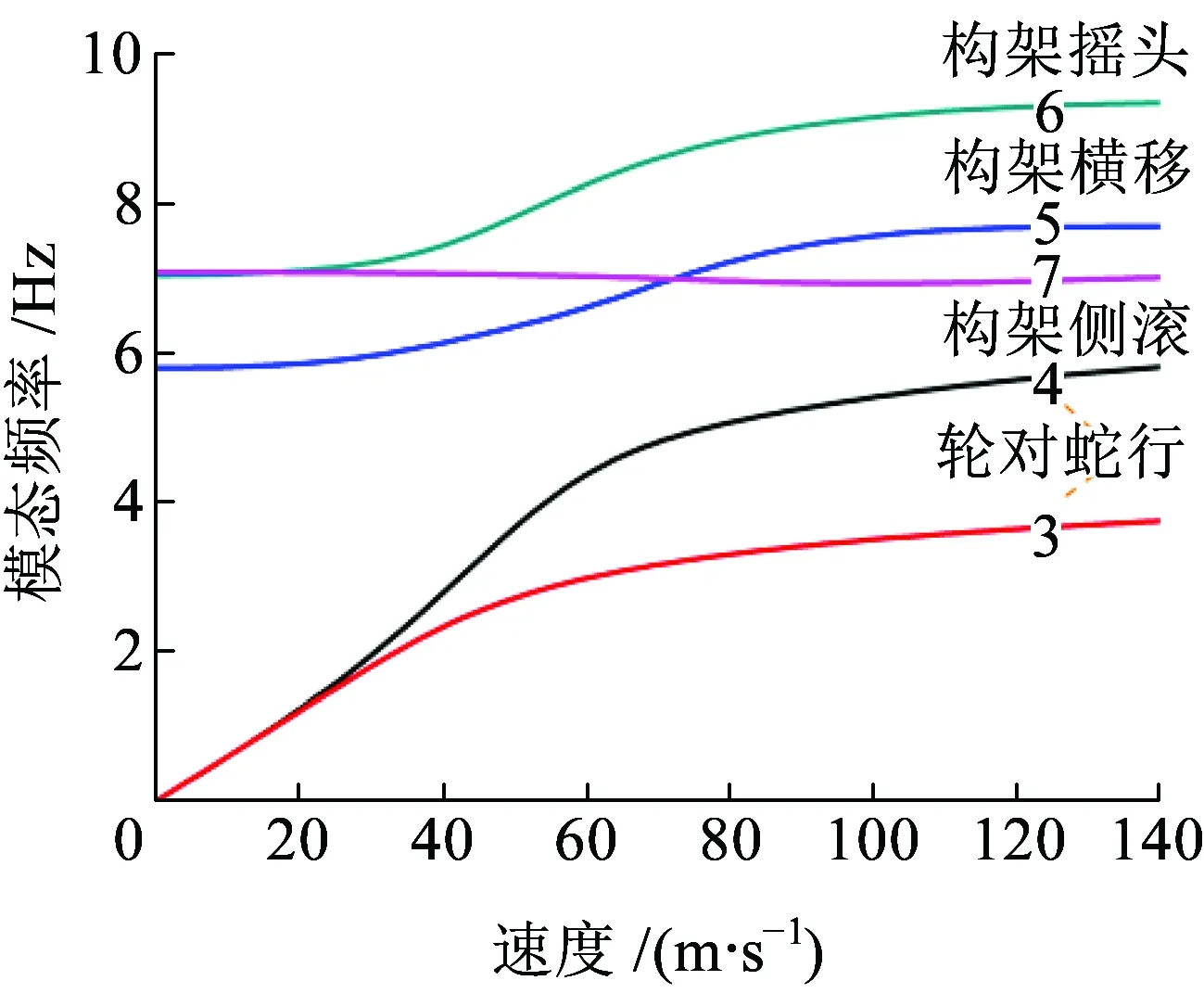
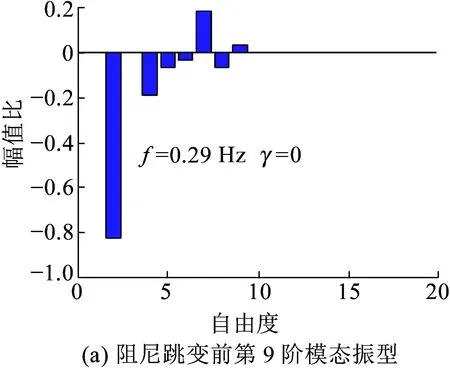
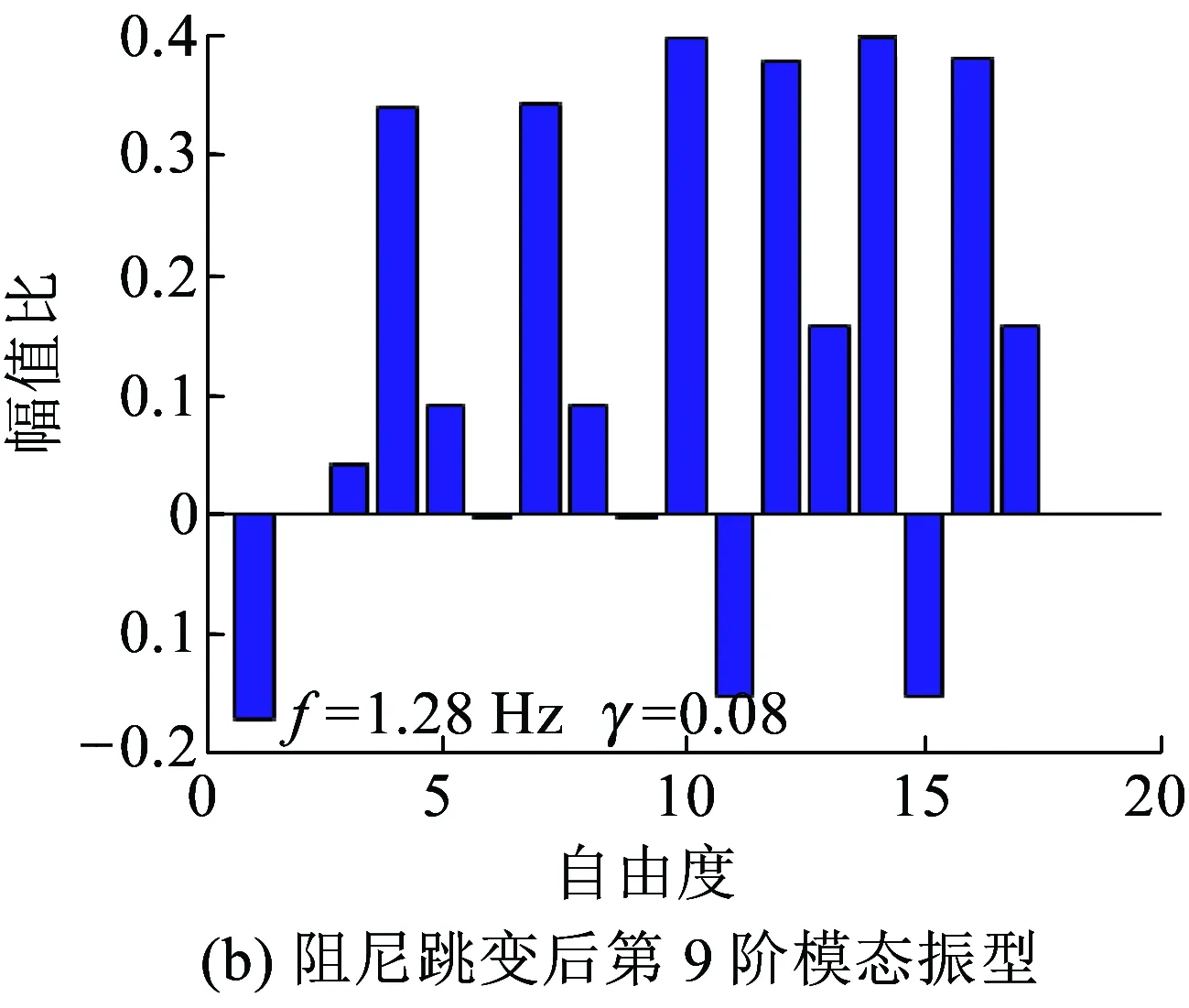
由于三次样条插值函数具有二阶连续导数[12-13],本节基于三次样条插值原理给出不同速度下模态频率的连续追踪方法。若函数s(x)在区间[a,b]上具有二阶连续导数,并且对于[a,b]上的分划a=x0 ( 6 ) 式中: 由于函数s(x)中含有m+3个待定系数,故应需要m+3个插值条件,已知插值节点xp处的给定函数值yp=f(xp)(p=0,1,…,m),此处提供了m+1个插值条件。在实际问题中,常在边界上补充另外2个插值条件,本文所补充的另外2个边界条件为 ( 7 ) f′(x0)、f′(xm)的值由首、末节点处的Lagrange插值[14]近似计算得到。 图2 模态连续追踪流程 考虑到车辆系统的模态阶数较多,为了更加清晰呈现不同速度下车辆系统各阶模态的发展规律,依次对不同速度下弹性定位轮对、转向架、整车展开复模态分析和模态追踪。 假定轮对通过横向和纵向弹簧与一个理想参考框相连,参考框只沿轨道按速度v前进,其振动可忽略不计。对于图3所示弹性约束轮对,其横移yw和摇头ψw运动方程为 ( 8 ) 式中:yw和ψw分别为轮对的横向位移和摇头角;mw和Iwy分别为轮对的质量和摇头惯量;f11和f22分别为纵向和横向蠕滑系数;kpx和kpy分别为一系纵向和横向刚度;W为轴重;λ为踏面等效锥度;b为轨距之半;lpy为一系悬挂横向跨距之半。 图3 弹性定位轮对动力学模型 在任一速度下,均可得到两个实部较大的复数特征根和1对模值较小的共轭复数特征根,由于与实部较大的复数特征根相对应模态的模态阻尼很大,其振动衰减速度很快,因此可不予考虑。图4为不同速度下弹性约束轮对模态频率,图中散点为复模态分析计算得到的离散模态频率,黑实线为模态追踪结果,红实线为轮对蛇行运动频率理论值[5]。从图4可以看出,当速度小于20 m/s时,弹性约束轮对模态频率实际值与理论值吻合良好,随着速度的提高,惯性力的影响不可忽略,此时弹性约束轮对模态频率实际值与理论值出现较大差异。图5为不同速度下弹性约束轮对模态阻尼比,由于一系悬挂刚度增加了蛇行运动恢复力,有效提高了轮对蛇行运动稳定性,当速度达到134 m/s时轮对蛇行运动才会失稳。 图4 不同速度下弹性约束轮对模态频率 图5 不同速度下弹性约束轮对模态阻尼比 建立转向架动力学模型如图6所示,整个转向架系统共有7个自由度,分别为转向架构架横移yt、摇头ψt、侧滚ρt,一、二位轮对横移yw1,2,一、二位轮对摇头ψw1,2,转向架系统任何一阶模态均包含这7个自由度的耦合振动信息。当速度为v,转向架系统运动方程为 ( 9 ) 式中:mt、Itr、Ity分别为构架质量、侧滚惯量以及摇头惯量;lpx为轴距之半;hbw为构架与轮对重心垂向距离。 图6 转向架动力学模型 对不同速度下转向架系统进行复模态分析发现,在任一速度下,转向架系统前两阶模态阻尼比接近于1,这两阶模态对转向架系统振动影响可忽略不计,因此本节针对转向架系统第3~7阶模态展开模态追踪。图7为转向架模态频率追踪结果,其中第3、4阶为以轮对振动为主模态,第5~7阶为以构架振动为主模态,当速度较小时,轮对模态频率随着速度的提高而线性上升,当速度进一步增大,轮对模态频率上升趋势变慢;以构架横移、摇头振动为主模态的模态频率缓慢上升,以构架侧滚振动为主模态的模态频率基本不变。由于一系悬挂刚度较大,在所有速度下,轮对模态频率和构架模态频率始终相差较大。 图7 不同速度下转向架模态频率 图8为不同速度下转向架系统第3~7阶模态的模态阻尼比,在所有速度下,未出现模态阻尼异常变化。当速度达到40 m/s时,第3阶模态的模态阻尼比小于0,轮对开始蛇行失稳。由于动力学模型中未考虑抗侧滚扭杆刚度,因此以构架侧滚振动为主模态(第7阶模态)的模态阻尼比一直为0,当模型中加入抗侧滚扭杆刚度后,以构架侧滚振动为主模态的模态阻尼比明显提升。 图8 不同速度下转向架模态阻尼比 建立整车动力学模型如图9所示,整车系统共有17个自由度,为车体横移yb、摇头ψb、侧滚ρb(1×3),前后构架横移yt1,2、摇头ψt1,2、侧滚ρt1,2(2×3),1~4位轮对横移yw1,2,3,4、摇 头ψw1,2,3,4(4×2),整车系统任何一阶模态均包含这17个自由度的耦合振动信息。当速度为v,整车系统运动方程为 图9 整车动力学模型 (10) 式中:mb、Ibr、Iby分别为车体质量、侧滚惯量以及摇头惯量;ksx、ksy、ksz分别为二系纵向、横向以及垂向刚度;lskz为二系悬挂横向距离之半;hstk为构架重心与二系悬挂垂向距离;hsck为车体重心与二系悬挂垂向距离;lt为定距之半。 对不同速度下整车系统进行复模态分析和模态追踪,在对整车系统进行复模态分析的过程中发现,在任一速度下,均可得到4对实部较大和13对实部较小的共轭复数特征根,此处仍不考虑前4阶模态对整车系统振动的贡献。图10为整车系统第5~17阶模态频率的追踪结果:由于前后构架按照车体中心呈对称分布,因此以前后构架横移(第12、13阶)、摇头(第14、15阶)、侧滚(第16、17阶)振动为主的模态频率曲线基本重合;第5、6阶为以轮对振动为主模态,第10阶模态为以车体侧滚振动为主模态;当速度上升至4.2 m/s和11.5 m/s时,第7与第9阶、第8与第11阶模态间出现频率转向现象,其特点为某一阶模态的模态频率随车辆运行速度的提高而不断增加,而另一阶模态的模态频率基本不变,所以两阶模态频率曲线不断接近,但是在速度接近4.2 m/s和11.5 m/s时,这种接近趋势不再继续,而是相互分离,表现为频率曲线间的转向,因此称之为频率转向。 图11为不同速度下整车系统第5~17阶模态阻尼比,当速度为4.2 m/s和11.5 m/s时,第7与第9阶、第8与第11阶模态间出现阻尼异常变化并且第7与第8阶模态阻尼比小于0,这种模态阻尼异常变化特点为某阶模态阻尼陡然增加且同时另外一阶模态阻尼下降明显,定义此现象为阻尼跳变。当速度进一步上升至48 m/s后,轮对开始蛇行失稳。 图10 不同速度下整车模态频率 图11 不同速度下整车模态阻尼比 为了更加清晰呈现发生阻尼跳变模态随速度的变化情况,分别提取第7、8、9、11阶模态频率和模态阻尼比(图12、图14、图16、图18),并给出阻尼跳变前后对应的模态振型(图13、图15、图17、图19)。以第7与第9阶模态为例,当速度为4.2 m/s时,第7与第9阶模态出现阻尼跳变现象,同时模态频率曲线开始转向。在出现阻尼跳变现象之前(1 m/s),第7阶模态振型以轮对横移振动为主,第9阶模态振型以车体摇头振动为主;在出现阻尼跳变现象之后(20 m/s),第7阶模态振型切换为以车体摇头振动为主,同时第9阶模态振型切换为以轮对横移振动为主。同样地,当第8与第11阶模态出现阻尼跳变现象时也出现了频率转向和振型切换现象。因此,轮对模态与车体模态间的振型切换是导致整车系统出现阻尼跳变现象的根本原因,该结论也同时充分说明了模态追踪结果的正确性。当发生阻尼跳变后,以车体摇头或横移振动为主模态的模态阻尼比明显下降甚至小于0,导致车体出现剧烈低频横向晃动。 总结以上分析可知:阻尼跳变现象都是在轮对模态频率接近车体模态频率时出现,其本质为随着车辆运行速度的提高,轮对模态与车体模态间的振型切换,并非轮对模态频率曲线“穿越”车体模态频率曲线产生的共振失稳。目前,在线运营铁道车辆的二系悬挂刚度较小,当速度较低时轮对模态频率就和车体模态频率非常接近,然而当轮对模态频率接近车体模态频率时并不一定就会产生阻尼跳变现象(比如第10阶模态),这与仅有部分铁道车辆会产生低频横向晃动的在线检测结果一致。由于现有文献和标准里缺乏车体低频横向晃动的指标判据,为此,本文接下来将研究铁道车辆出现阻尼跳变现象的指标判据,为降低并消除铁道车辆的低频横向晃动提供目标参考。 图12 不同速度下第7阶模态频率和模态阻尼比 图13 阻尼跳变前后第7阶模态振型 图14 不同速度下第8阶模态频率和模态阻尼比 图15 阻尼跳变前后第8阶模态振型 图16 不同速度下第9阶模态频率和模态阻尼比 图17 阻尼跳变前后第9阶模态振型 图18 不同速度下第11阶模态频率和模态阻尼比 图19 阻尼跳变前后第11阶模态振型 通过前述分析可知,轮对模态与车体模态间的“振型切换”是导致车体低频横向晃动的本质原因,因此,本节将基于轮对模态与车体模态间的振型相似度来研究铁道车辆出现车体低频横向晃动现象时的指标判据。为衡量两个样本之间的相似程度,常采用欧氏距离、马氏距离、切比雪夫距离、余弦距离、相关距离等距离函数[15-16]。若采用相关距离,则定义第i与第j阶振型相似度为 (11) 图20、图21分别是随着车辆运行速度的提高,出现振型切换现象两阶模态间(7&9,8&11)的振型相似度,当速度分别为4.2 m/s、11.5 m/s时,sim(7,9)、sim(8,11)出现非常接近于1的峰值,此时第7&9,8&11两阶模态间发生了振型切换。因此,以振型相似度作为铁道车辆是否出现车体低频横向晃动的指标判据是有效的。 图20 第7与第9阶振型相似度 图21 第8与第11阶振型相似度 通过对不同速度下弹性定位轮对、转向架、整车展开连续模态追踪,发现了阻尼跳变现象并研究了铁道车辆车体低频横向晃动的机理,得出以下结论: (1)基于Lagrange三次样条插值的模态连续追踪方法能够稳定、准确追踪车辆系统各阶模态,该方法适用于不同参数下多体动力系统的模态归属问题。 (2)轮对模态频率接近车体模态频率是出现车体低频横向晃动的必要非充分条件,轮对模态与车体模态间的振型切换是车体低频横向晃动的本质原因,并非轮对模态频率曲线“穿越”车体模态频率曲线时产生的共振失稳。 (3)当轮对模态与车体模态间发生振型切换时,对应速度下轮对模态与车体模态间的振型相似度接近1,基于振型相似度提出的车体低频横向晃动判定指标是合理、有效的。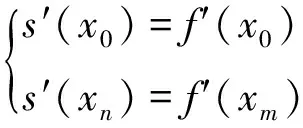


3 车体低频横向晃动机理研究
3.1 弹性约束轮对模态连续追踪
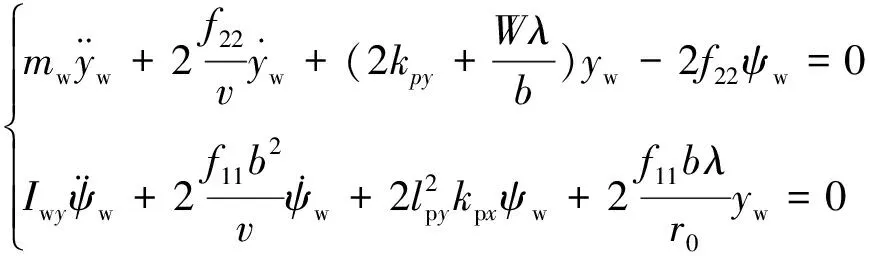



3.2 转向架模态连续追踪



3.3 整车模态连续追踪













4 基于振型相似度的车体低频横向晃动指标研究



5 结论
