变坡度轨道几何线型的试验台模拟方法

刘玉梅，庄娇娇，郭艳秀，熊明烨，赵聪聪

(1.吉林大学交通学院，吉林长春 130022；2.北京新能源汽车股份有限公司，北京 102600；3.伊利诺伊大学电气与计算机工程系，乌尔瓦纳 IL61801；4.吉林农业大学工程技术学院，吉林长春 130118)

为保证高速列车运行的平稳性，在线路地形变化区段一般需要设置纵向坡度或修建隧道或桥梁，其中，设置纵向坡度可以在保证列车平稳运行的基础上，还能大幅节省修建工程成本。故列车运行时，不可避免地会通过具有纵向坡度的线路段。近些年来，随着我国机车车辆各项技术的提升，高速列车的动力性能和制动性能也有了更高的安全保障，使其可以实现在较陡线路坡度上的安全行驶，因此，轨道线路的最大坡度标准也在逐步放宽[1-4]。

为了研究轨道车辆系统的曲线通过性能，国内外学者越来越广泛的利用模拟试验台。如德国的滚振试验台能够实现轨道车辆整车实际轨道激扰下的直线、曲线动态模拟以及模态分析[5]。文献[6]开发了3自由度实物转向架防地震振动试验台[6]。长沙机务段与有关单位合作开发了机车转向架模拟负载运行试验装置，可以模拟机车上坡、下坡和曲线运动[7]。

本文借助于课题组所开发的转向架动态模拟试验台的下部双六自由度运动平台，研究轨道变坡度的室内模拟方法。基于变坡度轨道几何线型的特征和双六自由度运动平台的结构参数，建立双六自由度运动平台的位姿反解模型以及坡道模拟所对应的运动平台的位姿转化模型，利用MATLAB/Simulink实现某一变坡度轨道几何线型下双六自由度运动平台的位姿反解解算。本文的解算结果不仅为室内模拟变坡度轨道的双六自由度运动平台的仿真控制提供了参数依据，同时也为进一步研究纵向坡度对转向架性能的影响奠定了基础。

1 变坡度轨道模拟器及位姿反解模型

1.1 变坡度轨道模拟器

本文所借助的轨道模拟器主要由双六自由度运动平台组成。该六自由度运动平台通过多组协调作用的作动器为钢轨提供横向、纵向和垂向作用力，并通过固装在作动器及六自由度运动平台上的三维力和位移传感器来实时测量在模拟运动过程中的位移和作用力。由于任意运动平台均可在作动器的作用下实现沿X、Y、Z轴平移以及绕X、Y、Z轴转动的六自由度运动，所以该轨道模拟器能够实现各种轨道线型与轨道不平顺的动态模拟，具体结构如图1所示。

图1 变坡度轨道模拟器的三维模型

1.2 模拟器位姿反解模型

设列车的前进方向为X轴，横向为Y轴，垂直方向为Z轴，根据双六自由度运动平台的几何结构，首先选取双六自由度运动平台8个垂向作动器的下铰链点所在平面中心为定坐标系原点O，建立定坐标系O-XYZ；同时，选取平台1、平台2的轮对与夹具的两个切点中点为两个局部坐标系原点O1、O2，分别建立平台1和平台2的局部坐标系，即O1-X1Y1Z1和O2-X2Y2Z2。

双六自由度运动平台包括平台1和平台2，平台1、平台2上分别放置转向架的一位轮对和二位轮对。由图1可知，每个平台中分别包含：4个垂向作动器，其关于平台局部坐标系的X轴和Y轴对称布置；2个纵向作动器，其关于平台局部坐标系的X轴对称布置，且作动器铰链点在平台局部坐标系的Z轴坐标为0；1个横向作动器，横向作动器在整体上关于定坐标系的Y轴对称布置，且作动器铰链点在平台局部坐标系的X轴、Z轴坐标均为0。平台的几何结构参数见表1。为了表述方便，将作动器与运动平台的铰接点定义为上铰链点，将作动器与铸铁平台或反力支座的铰接点定义为下铰链点。

表1 结构参数

确定双六自由度运动平台14个作动器的铰链点在定坐标系的坐标表示是解算平台位姿的前提，本文利用齐次坐标表示铰链点的空间位置。由于作动器的下铰链点固定安装在铸铁平台上，故不会产生任何位移和转动，因此只需引入齐次变换矩阵表示上铰链点在空间的平移和转动即可。根据双六自由度运动平台的结构参数(表1)，可得到各作动器的上、下铰链在其局部坐标系中的坐标。

作动器1.1～1.7的上铰链点A1在局部坐标系O1-X1Y1Z1中的坐标向量可以表示为

( 1 )

作动器1.1～1.7的下铰链点B1在局部坐标系O1-X1Y1Z1中的坐标向量可以表示为

( 2 )

作动器2.1～2.7的上铰链点A2在局部坐标系O2-X2Y2Z2中的坐标向量可以表示为

( 3 )

作动器2.1～2.7的下铰链点B2在局部坐标系O2-X2Y2Z2中的坐标向量可以表示为

( 4 )

利用广义坐标Pi=(αi,βi,γi,li,mi,ni) (i=1,2)描述局部坐标相对于定坐标的位姿，其中，αi、βi和γi为局部坐标系相对于定坐标系绕X、Y、Z轴的姿态角;li、mi和ni为局部坐标系相对于定坐标系沿X、Y、Z坐标轴的平移量。

根据文献[8-9]定坐标(静坐标)与局部坐标(动坐标)的转换方法可知，两个模拟平台的空间齐次变换矩阵Ti(i=1, 2)可以表示为

( 5 )

各作动器上、下铰链点之间位置向量关系为

(6)

伸缩量可以表示为

( 7 )

2 变坡度轨道模拟

坡道的坡度一般规定为上坡为正，下坡为负，平道为零。平道与坡道、坡道与坡道的交点称为变坡点。根据GB 50090—2006《铁路线路设计规范》[10]，道路路线纵断面是沿道路中线竖直剖切后再展开得到的，根据铁路等级、行车速度、工程条件、地形类别和牵引种类等因素将路线纵断面设计成一条有起伏的空间线。纵断面设计线由直坡线和竖曲线组成，如图2所示。下面将利用双六自由度运动平台分别模拟分析直坡线和竖曲线的轨道坡度。

图2 纵断面设计线示例

2.1 直坡线坡道的模拟

在模拟坡度为ir‰的纵向坡道时(图2中的A1-A2段)，由于转向架通过车轮夹具与运动平台固定，可将两个台面视为一体，并将平台1或平台2的中心作为运动参考点，以简化计算。

本文选取平台1的中心为参考点，两平台绕通过该点的Y轴做旋转角为θr的圆周运动。图3所示为模拟直坡线坡道时双六自由度运动平台的状态图，其中O1、O2分别为双六自由度运动平台中心的初始位置，O1′、O2′分别为双六自由度运动平台中心运动后的位置，θr=arctan(ir‰)。

图3 直坡线坡道的静态模拟

当双六自由度运动平台处于中位时，两模拟平台的位姿分别为

( 8 )

结合坡度定义、车辆的运动规律以及平台的几何结构尺寸对图3的几何关系进行分析计算，得到平台的旋转量和平移量为

( 9 )

式中：Δαi、Δβi、Δγi分别为平台的局部坐标系相对于定坐标系绕X、Y、Z轴的旋转量；Δli、Δmi、Δni分别为沿X、Y、Z轴的平移量(i=1,2)。

两运动平台的位姿分别为

(10)

将得到的运动平台的理论位姿输入上述位姿反解模型并进行解算，即可得到14个作动器的伸缩量，从而可控制平台运动以实现变坡度轨道线型的模拟。

2.2 变坡处竖曲线坡道的模拟

竖曲线是一种在线路垂直面上的曲线，当两相邻坡度的代数差达到一定值时，应在相邻坡段间用圆曲线进行连接，以改善列车的运行环境，从而保证列车安全平稳运行。

《铁路工程技术规范》[11]规定，最大相邻坡段的坡度代数差不得超过重车方向的限制坡度值。Ⅰ、Ⅱ级铁路相邻坡段的坡度代数差大于3‰、Ⅲ级铁路大于4‰ 时，应以竖曲线连接[11]。线路所采用的竖曲线按形状可分为3种：圆曲线形竖曲线、抛物线形竖曲线、连续短坡(链条坡)形竖曲线。

(1)圆曲线形竖曲线坡道的模拟

在直线坡段的变更处，用一个半径较大的圆弧把相邻两个坡段连接起来的竖曲线，称为圆曲线形竖曲线。当列车行驶在如图4所示的圆曲线形竖曲线坡道时，车轮与路面的切点C1、C2同时处在同一圆弧线上，设圆弧方程为(x-a)2+(z-b)2=R2(其中a、b和R均为已知值)。模拟圆曲线形竖曲线坡道时(图2中的A2-A3段)，点C1、C2在轨道模拟器中分别对应于平台的中点O1、O2。根据圆弧方程及车辆的运动规律，将自变量为x的函数转变成自变量为t的函数，即

(11)

结合列车行驶速度、路线几何线形可得C1、C2的坐标为

(12)

两运动平台与水平面所成夹角的变化规律为

(13)

两运动平台的旋转量和平移量为

(14)

经上述分析得出，模拟圆曲线形竖曲线坡道时，两运动平台的位姿分别为

(15)

图4 车体在圆曲线形竖曲线坡道上的模拟

(2)抛物线形竖曲线坡道的模拟

抛物线形竖曲线的曲度逐渐变化，将一端的坡度缓缓变化而成为他端的坡度，其图形与抛体运动的轨道形状相同。该曲线轨道的模拟方法与圆曲线形竖曲线坡道的模拟方法相同，在此不再赘述。

(3)连续短坡形竖曲线坡道的模拟

连续短坡是由许多坡度逐渐变化的连续短小直线组合而成，这些坡度不同的短小直线构成一个很平缓的纵断面。列车通过该坡段可分为两种情况，一种是车体的前后车轮处在同一坡度的坡段上；另一种是车体的前后车轮处在不同坡度的坡段上。前一种情况与上述直坡线坡道的模拟相同。后一种情况(图5)下道路的折线方程可表示为

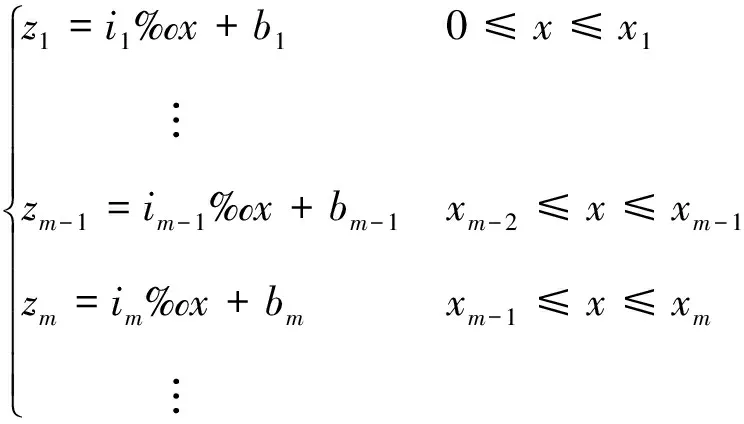
(16)

将自变量为x的函数转变成自变量为t的函数，有

(17)

车轮与路面切点C1、C2的坐标可以表示为

(18)

经上述分析得出两运动平台的位姿分别为

(19)

图5 车体在连续短坡形竖曲线坡道上的模拟

由于实际纵切面的坡道线是由多种坡段组合而成，所以在模拟变坡度坡道时需分段进行，将输入部分以时间t为变量划分成多个时间段并分别建立坡道的模拟输入函数。每个阶段的输入函数可参照上述坡道线路的模拟方法进行确立。

3 坡度模拟仿真及验证

3.1 坡度模拟仿真

基于上述理论分析，利用Simulink建立坡度模拟仿真模型，如图6所示。该模型主要包括期望坡度输入模块、平台位姿协调转化模块、坐标变换模块、作动器位移解算模块以及输出显示模块。其中平台位姿协调转化模块根据期望坡度及双六自由度运动平台的位姿协调关系，输出双六自由度运动平台位姿。

本文选取转向架常见轴距L=2 500 mm，列车速度根据实验要求确定，这里为后面计算方便选择列车速度为v=72 km/h。设列车驶入图2所示的变坡度坡道，并对该线型坡道进行仿真模拟，对双六自由度运动平台进行位姿反解解算。根据图6的Simulink坡度模拟仿真模型，得到作动器的实时位移解算结果，如图7所示。

图6 坡度模拟仿真模型

图7 平台作动器位移

3.2 仿真验证

为验证文中平台1与平台2的位姿反解数学模型、位姿转化模型以及坡度模拟仿真模型的正确性，结合图2、图3所示的变坡度时轨道模拟器的运动状态，通过对比几何解析方法计算作动器的伸缩量与仿真模型解算的结果进行分析。鉴于篇幅的限制，此处仅以25‰ 坡度值下作动器2.1、2.3、2.5及2.7为例计算作动器的伸缩量。当列车完全驶入坡度为25‰ 的坡道时，各作动器的伸缩量见表2。

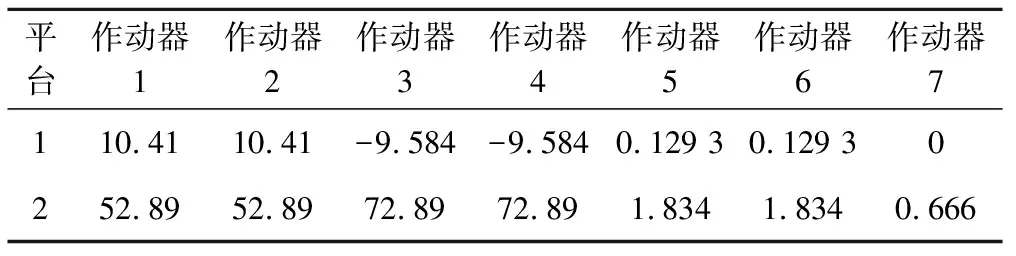
表2 坡度值为25‰ 时作动器各自伸缩量 mm

因此，作动器2.1的上铰链点A21和下铰链点B21相对于O1的初始二维坐标为

(20)

(21)

结合直角三角形相关理论可得

(22)

进一步可求得A21′的坐标为

(23)

(24)

根据向量范数可得

(25)

作动器2.1的伸缩量为

(26)

根据表1的结构参数，将x1=400 mm，z1=990 mm，z2=3 920 mm，l0=1 250 mm带入可得ΔL21=ΔL22=52.89 mm。同理可得，ΔL23=ΔL24=72.89 mm，ΔL25=ΔL26= 1.834 mm，ΔL27=0.662 mm。仿真模型计算得到的伸缩量为：ΔL21= ΔL22=52.89 mm，ΔL23=ΔL24=72.89 mm，ΔL25=ΔL26= 1.834 mm，ΔL27=0.666 2 mm。由上述可知，利用仿真模型解算得到的作动器伸缩量与几何分析法得到的结果具有较好的一致性，从而验证了该双六自由度运动平台位姿反解仿真模型以及本文坡道线路的模拟方法的正确性。

4 结束语

本文基于变坡度轨道几何线型的特征和双六自由度运动平台的结构参数，建立双六自由度运动平台的位姿反解模型以及坡道模拟所对应的平台位姿转化模型，并且借助MATLAB/Simulink搭建了变坡度模拟仿真模型，进而对列车在某段变坡度线路行驶情况进行了仿真。本文以模拟列车驶入坡度25‰的坡道为例，通过几何解析方法对作动器伸缩量进行计算，并与位姿解算模型结果进行比较，从而验证了本文所建模型的正确性。本文的解算方法为室内模拟变坡度轨道的双六自由度运动平台的仿真控制提供了参数依据，同时也为研究变坡度下车辆或转向架的性能奠定了基础。