制动盘摩擦环厚度对其热容量和热应力的影响
2019-01-18周素霞赵兴晗周大军郭子豪卢术娟
周素霞 , 赵兴晗 , 周大军, 郭子豪 , 徐 鹏 , 卢术娟
(1.北京建筑大学机电与车辆工程学院, 北京 100044;2.北京建筑大学城市轨道交通车辆服役性能保障北京市重点实验室, 北京 100044;3.武汉武铁车辆有限公司,湖北武汉 430012)
我国高速列车运行速度恢复至350 km/h后,其制动性能更加被重视。目前高速铁路采用的制动方式主要是盘式制动,具有结构简单、工作可靠等优点[1]。实际工作过程中,制动盘是能量转换装置,将列车的动能通过摩擦作用,转换为热,散发至大气中。在制动过程中制动盘温度急速上升,制动结束后又逐渐冷却,这种冷热交替循环产生的热负荷会引起龟裂纹和热疲劳[2-5],继续使用会导致裂纹持续扩展,引发重大事故。因此,在制动盘的研发阶段,需要对其热容量进行分析,确定能够满足运行要求。
国内外对制动盘热容量计算由来已久,文献[6]对制动盘的热行为进行了仿真分析并与实验结果进行了对比分析。文献[7]通过数值法代入温度边界条件,对带有通风结构的制动盘进行仿真分析并得到制动盘的热应力场、温度场及温度随时间变化曲线,提供了一种计算温度场引起制动盘失效的手段。文献[1]采用有限元法对3种不同材料制动盘的热特性进行了对比分析,为制动盘结构的设计与优化提供了参考。文献[8]采用将制动盘散热转化为逆向热流密度的方法对制动盘的温度场进行了仿真分析,得到铸铁制动盘温度的最大值。文献[9]围绕轿车制动盘加强筋对其散热性能进行了分析,通过改变制动盘加强筋的数量及侧宽度提高其散热性能。对制动盘的研究主要是摩擦环为标准厚度时制动盘热容量的分析计算,而较少研究摩擦环厚度对制动盘热容量的影响。因此需要研究摩擦环厚度对制动盘热容量的影响,为制动盘的寿命计算和使用提供参考。
制动盘在服役期间会出现磨耗或划痕,在检修时缺陷若超过界限会回厂返修打磨,使得制动盘摩擦环厚度减小。本文采用间接耦合的方法对新型动车组制动盘厚度进行仿真分析,研究厚度对制动盘热容量的影响规律。
1 理论模型
1.1 制动盘热载荷模型
动车组从运动状态到静止,列车的动能经过制动盘的作用转化为热能散发到大气中。假设制动过程中列车的动能全部转化为热能,制动过程中所产生的热量为[10-11]
( 1 )
式中:W为动能;M为轴重,kg;v0为初速度,v1为末速度,m/s。
但在实际制动过程中,还存在轮轨之间的摩擦与空气阻力,所以列车的动能并没有全部通过制动盘进行转换,并且摩擦副在工作时,闸片也吸收了部分热能。综合考虑上述情况,制动盘吸收热能占总动能的百分比为[12]
( 2 )
式中:k、c、ρ分别为导热系数、比热和密度;下标p代表闸片材料;下标d代表制动盘材料。制动盘摩擦环输入的热量为
Q(t)=ηW/n
( 3 )
式中:n为每根轴上制动盘的数量。
假设制动盘摩擦环上的热量是均匀分布的,根据热流密度定义得到制动盘摩擦环上热流密度与时间t的关系为
( 4 )
q(t)=-ηMa(v0+at)/(2nA)
( 5 )
式中:η为散热效率,η=0.798;M为轴重,M=14 t;v0为初始速度,v0=84 m/s;a为加速度,a=-0.93 m/s2;n为每根轴上制动盘数量,n=3;A为摩擦面积,A=0.2 m2。
1.2 热对流模型
在制动过程中制动盘散热分为两个部分:静止时为自然对流换热,制动时为强制对流换热。对流换热的表达式为
h=(ρ,ν,μ,cp,L)
( 6 )
从式( 6 )可以看出,制动盘的对流换热系数与其材料并无关系,而取决于流体的流动状态、流体物理性质、表面尺寸和制动盘的几何形状。将制动盘表面的对流换热转化为平面散热,根据平面散热问题的传热理论得到
( 7 )
式中:L为壁面长度,m;u∞为空气的流动速度,m/s;γ为空气运动黏度,m2/s;Pr为普朗特数;λa为空气的导热系数。由式( 7 )可以看出,α与壁面长度、空气流动速度和空气导热系数成正比,与空气运动黏度和面壁长度成反比,但一般在计算时会忽略制动盘温度变化对周围空气的影响,则α只与L和u∞有关。
1.3 热辐射模型
热辐射被称为辐射换热,是3种热传导方式之一。它是由于物体内部微观粒子的热运动使物体向外发射辐射能的现象[11]。在热辐射的计算中一般引用斯蒂芬-玻尔兹曼定律的公式来分析热辐射能。
( 8 )
式中:ε为辐射率;σ为斯蒂芬-玻尔兹曼常数;Ts为表面绝对温度;T0为环境绝对温度。
2 制动盘有限元模型
采用ANSYS进行有限元分析,研究对象为轴装制动盘,具有对称结构[13-15]。为节省计算时间,取制动盘1/10进行仿真分析。网格划分时对摩擦环处网格进行细化,采用Solid70单元,以增加计算精度,其余部分采用较大尺寸网格,进一步节省计算时间。1/10制动盘离散化模型共计54 110个单元,如图1所示。在计算厚度对制动盘热容量影响时,只改变制动盘摩擦环厚度,网格数量并未改变。

图1 离散化模型
3 厚度对制动盘热容量的影响
3.1 厚度对制动盘温度场的影响
本文主要计算列车运行速度为300 km/h时制动盘摩擦环厚度对制动盘热容量的影响,根据计算需在摩擦环上施加热流密度的时间为91 s。制动盘初始厚度为23 mm,每减小0.5 mm计算一次,得到不同厚度下铸钢制动盘温度场云图,如图2、图3所示。

图2 厚度23.0 mm温度云图

图3 厚度19.0 mm温度云图
从图中可以看出,厚度为23.0 mm时最高温度为333.01 ℃,厚度为19.0 mm时最高温度为362.21 ℃。最高温度位于制动盘摩擦面。摩擦面上出现较为明显的温度梯度,由于摩擦环生热面温度最高,在制动过程中热量由摩擦面向散热筋、盘爪转移,距离摩擦面越远温度越低。选取不同厚度时摩擦面上相同位置的点,分析厚度对其温度和热应力的影响。绘制制动过程中温度变化曲线,如图4所示。
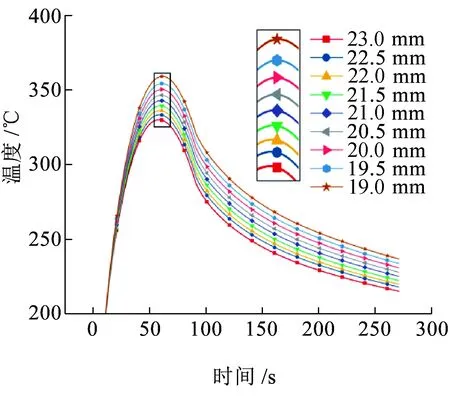
图4 不同厚度下盘面温度变化曲线
由图4可以看出:在制动初期,制动盘盘面温度急剧上升,在t=62 s时到达最高值,之后温度开始下降,在制动结束后温度缓慢下降。制动初期产生的热量主要集中在盘面,未到达散热筋处,所以散热效果不明显,不同厚度下盘面的温度基本相同。由图5可以看出,在速度为300 km/h工况下,t=62 s时厚度为23.0 mm与19.0 mm温度相差29.61 ℃。温度变化基本呈线性关系。在厚度减少5 mm的情况下温度提升8.24%。与速度为350 km/h的工况下温度变化趋势进行对比,两种工况下温度随厚度的变化趋势基本一致。

图5 摩擦环厚度与最高温度关系曲线
3.2 厚度对制动盘应力场的影响
在制动时,由于制动盘不同区域温度分布不均匀,热应变有阻碍,产生热应力。本文采用间接耦合方法分析计算热应力场,即将温度场的计算结果作为计算热应力时的初始有限元分析模型,制动盘在制动过程中诸多原因会使其产生形变和应力,主要包括热应力、离心力、闸片压力、摩擦力、震动造成的应力,但对制动盘寿命影响最大的是制动时温度变化所造成的热应力。因此计算制动盘厚度对制动盘应力的影响仅从热应力的角度考虑。
3.2.1 热应力计算
将温度场计算结果作为应力场的载荷进行计算,首先将制动盘盘毂和装配孔进行全约束。由于分析对象为制动盘的十分之一,所以在模型两侧施加对称约束。制动盘在受到温度场和机械应力作用下的有限元方程为
( 9 )

热应力计算方程为[10]
σ=aE(T-T0)
(10)
式中:σ为热应力,MPa;a为线膨胀系数,a=1.06×10-5℃-1;E为弹性模量,E=2.08×105MPa;T0为初始温度,℃;T为某时刻温度,℃。
3.2.2 厚度对制动盘热应力的影响
采用间接耦合的方法对制动盘的热应力场进行仿真计算,得到制动盘不同厚度下制动盘的热应力[16-18]。图6、图7分别给出摩擦环厚度为23.0、19.0 mm工况下制动盘的热应力云图。

图6 厚度23.0 mm热应力云图
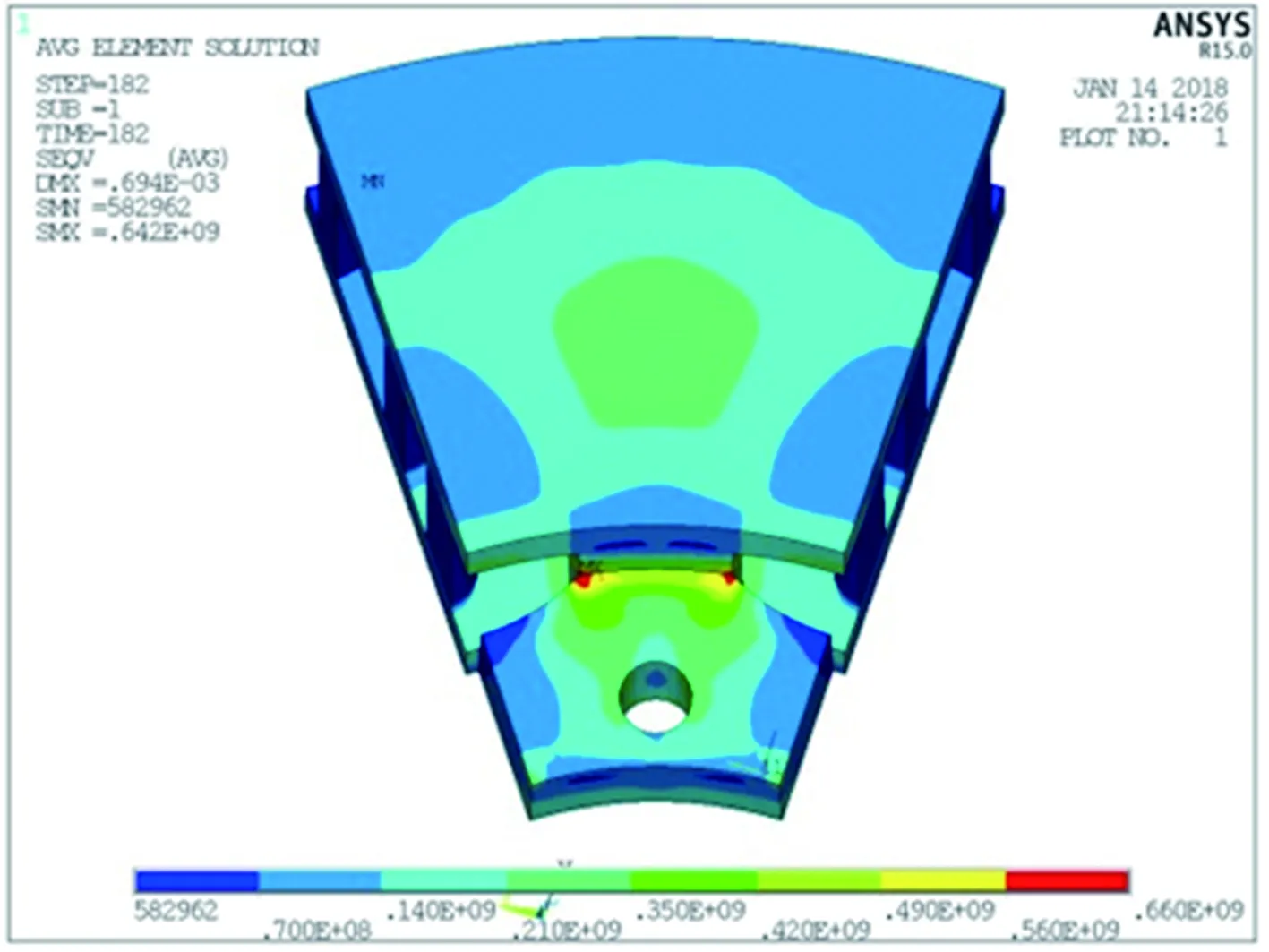
图7 厚度19.0 mm热应力云图
图8为制动盘摩擦环厚度为23.0、21.5、20.5、19.0mm时制动盘盘面在统一图例后的热应力云图。从图8可以看出,在制动盘盘面厚度为23.0 mm时,盘面最大热应力为140.0~210.0 MPa,随着厚度的降低,上述范围热应力区域面积变大,并出现更高的应力梯度。由于制动盘摩擦环厚度降低,在制动时最高温度数值增加,由于物体热胀冷缩的特性,温度更高时形变量增加,而摩擦面不能自由形变使热应力变大。图9为制动盘摩擦面处热应力随时间的变化曲线,所选点与图4盘面厚度温度变化曲线规律相同。图9中,厚度为23.0 mm时热应力曲线最低,随着厚度减小,热应力随之增大,这与温度曲线相似,在60~70 s时摩擦面热应力达到最大值。图10为62 s时不同摩擦环厚度在两种不同工况下的热应力变化曲线。由图10可知,在两种工况下热应力随厚度的增大而减小,速度为300 km/h,在62 s时厚度为23.0 mm与19.0 mm热应力相差47.72 MPa,盘面热应力随厚度的减小间距越来越大,厚度减小5 mm时,热应力增加12.82%,增加的热应力使得该部位在制动时更容易出现疲劳裂纹。由温度曲线与热应力曲线比较可知,摩擦环厚度对制动盘应力场的影响要高于其对温度场的影响。两种工况下应力随厚度的变化趋势也基本一致,验证了其变化趋势的有效性。

图8 4种厚度下制动盘热应力云图

图9 不同厚度下盘面热应力变化曲线

图10 摩擦环厚度与热应力关系
4 结论
本文以新型城际列车铸钢制动盘为研究对象,采用间接耦合的方法计算列车速度为300 km/h时,制动盘摩擦环厚度对制动盘热容量的影响,通过分析计算得到以下结论:
(1)从温度曲线变化可以得到,制动盘摩擦环厚度在制动初期对温度变化并无影响,在制动时间约15 s后温度开始发生差异,制动盘盘面温度随着厚度的减小而增加。制动盘盘面温度与厚度基本呈线性关系。制动盘厚度为23.0 mm时盘面温度333.01 ℃,厚度减小5.0 mm后,制动盘盘面温度增加约8.24%。
(2)从制动盘热应力云图和应力曲线可以得到,随着制动盘厚度的减小,摩擦面的热应力明显增大。盘面采样点的应力随着厚度的减小而增大,不同厚度的应力差距随着制动时间的增长而变大,随着厚度的降低最大应力变化速度略微有增加,在厚度为23.0 mm时,盘面采样点的热应力为371.98 MPa,在厚度减小5 mm时,热应力增加约12.82%。
(3)由仿真结果可知,随着制动盘摩擦环厚度降低,制动盘热容量随之降低,摩擦环厚度对应力场的影响要高于对温度场的影响。仿真结果为新型城际列车制动盘在不同厚度下寿命的预测提供了依据。
