电气化铁路多车网级联系统低频网压稳定性研究

母秀清，王 英，何正友，胡海涛，李琪瑶

(1.西南交通大学电气工程学院，四川成都 611756；2.兰州交通大学自动化与电气工程学院，甘肃兰州 730070)

截至2017年底，全国铁路营业里程已达到12.7万km，铁路电气化率、复线率分别居世界第一和第二位。但快速发展的电气化铁路运营也出现了较多问题，比如暂态过电压、高频谐波谐振[1]、低频网压振荡[2]、电磁干扰[3]等。

在这些问题中，电气化铁路低频网压振荡出现的时间相对较晚，我国是在全面引入大功率交直交电力机车和髙速动车组(以下简称“电力机车”)后出现了3～7 Hz低频网压振荡现象[4-5]。不同于电力系统的低频振荡，电气化铁路车网系统的网侧低频振荡属于运营中出现的车网电气匹配问题[6]。2009年12月以来，上海南翔动车所CRH1型动车组，数次因牵引网侧电压波动引起电力机车牵引封锁。2010年9月在北京、沈阳、郑州等地动车所出现了CRH5型动车组牵引封锁，造成动车组无法正点发车。2011年3月北京南站动车所30台机车启动时均出现因网侧低频电压波动牵引封锁状况。2011—2016年徐州所频繁发生低频网压振荡，多次造成HXD1B、HXD2B型机车牵引封锁，图1为徐州所多辆HXD2B型机车投入系统网测电气量低频振荡实测图[7]。

图1 徐州所多辆HXD2B机车投入系统网测低频振荡实测图

针对电气化铁路牵引供电系统网压低频振荡现象，目前国内外均已开展一定研究。国外学者介绍了电力机车同时投入运行时引起的频率为5 Hz的网压低频振荡，发现同时运行的机车数量及其控制系统参数会对车网低频振荡有较大影响[8-9]；国内学者主要通过网测低频振荡机理[5,10-11]、低频网压振荡抑制[4-5,12-13]和低频振荡稳定性[2,12,14-15]几方面进行研究。

电气化铁路网压低频振荡的已有研究表明，除去车网系统投入的电力机车台数外，牵引网中的电容、电感等参数和电力机车牵引变流器的控制参数、控制策略等都是引起车网发生网侧电压低频振荡现象的因素。此外，已有研究牵引网电压波动中机车研究对象多为dq解耦控制的CRH5型动车组，而其他车型投入系统的低频网压振荡研究相对较少。随着越来越多的交直交型列车投入运营，车网系统低频网压振荡使机车发生牵引封锁的概率也在不断增加。

本文针对近年来我国徐州所频繁发生的低频网压振荡问题，主要对该线路的HXD2B型车网系统进行低频网压振荡分析，并重点从系统稳定性角度进行研究。首先对牵引供电网和HXD2B型电力机车进行等效数学描述；依据较保守的禁区改进判据对该车网级联系统进行稳定性分析，并对车网系统各参数对系统稳定性影响进行评估分析；最后对多车整备时和不同阈值参数下的车网级联系统稳定性进行测试验证，并将结果与徐州所实测数据相比较，最终验证了系统稳定性分析结果的有效性和不同参数对系统稳定性影响研究的正确性。

1 车网级联系统数学描述

对电气化铁路车网系统进行稳定性分析，需先对系统进行数学描述。图2为徐州站全并联AT复线单相工频交流2×27.5 kV牵引供电示意图。

图2 全并联AT复线牵引供电系统示意图

图2的全并联AT复线牵引供电系统可等效简化为一个级联系统，如图3所示。该级联系统主要包括牵引供电网(主要包括牵引供电网和牵引变压器)和电力机车负载两大模块。

图3 车网级联系统等效示意图

图3中，US为27.5 kV交流电压源，IS为牵引变电所网侧电流，Zeq为未考虑牵引变压器阻抗时折算至27.5 kV侧的牵引网等效阻抗，ZS为牵引变电所变压器等效阻抗，C为牵引网对地电容，Zo为牵引供电网等效输出阻抗，Zin为电力机车等效输入阻抗。

1.1 牵引供电网等效阻抗Zo数学描述

图3中的牵引网等效阻抗Zo，主要包括牵引变电所变压器等效阻抗ZS、牵引供电网等效阻抗Zeq和牵引供电网对地电容C。

图2中，徐州北牵引变电所由110 kV外部电源接入，牵引变电所采用的是平衡变压器，这里使用Scott接线平衡变压器，Scott平衡变压器接线和等值电路如图4所示。

图4 Scott接线平衡变压器等值电路

针对全并联AT复线供电方式的牵引网阻抗Zeq进行计算，主要有等值电路法[16]和广义对称分量法[17]。针对全并联AT供电方式上下行接触网和正馈线对称分布的特点，采用考虑AT漏抗的牵引网广义对称分量法。该方法经过坐标变换后，钢轨自阻抗及其对接触线和馈线互阻抗均为零，在考虑AT漏抗的牵引网广义对称分量法计算中，不考虑钢轨影响[18]，将其他上下行接触网和馈线等效为4个电路支路，得出全并联AT牵引网复合序网如图5所示。

图5 全并联AT牵引网复合序网

图5中E′为全并联AT复线55 kV电压源，ITL0～3为各序电流，z0～z3为各序阻抗，ZL为负荷阻抗或短路阻抗。AT漏抗为

( 1 )

由文献[18]推导得到复线AT牵引网单位阻抗变换矩阵为

( 2 )

式中:下标T、F分别表示接触网和馈线；下标U、D分别表示上下行；A4为定义的四阶转换矩阵，用于将具体不同地电气物理量转换为对应的对称分量。

( 3 )

依据广义对称分量法，最终得到全并联AT复线供电方式的牵引网阻抗Zeq为

( 4 )

式中：x为牵引负荷在AT段中的位置；l为牵引负荷距供电臂首端的距离；D为两个AT所之间距离。

根据图3，求得牵引网阻抗Zeq后，结合牵引网对地电容C和牵引变压器等效阻抗ZS，AT牵引网等效输出阻抗为

( 5 )

为便于后续HXD2B型车网级联系统稳定性计算分析，在此给出徐州北牵引供电系统主要电气参数见表1。

表1 徐州北牵引供电系统主要参数

1.2 HXD2B机车负载等效阻抗Zin数学描述

1.2.1 HXD2B机车负载主电路

HXD2B型机车有3个主变流器柜，变流环节采用整流器多重化结构，每个主变流器柜中拥有2个整流器，故该机车拥有6个完全相同的变流环节，机车主电路结构示意如图6所示。图6中，uab为HXD2B车载变压器二次测电压，L2和C2为滤波环节，Cd为支撑电容，ud为输出直流电压。

图6 HXD2B机车主电路结构示意图

车网系统发生低频振荡时，列车大多处于轻载与整备状态，机车只开辅机系统，输出电流较小，牵引电机功率也较小，对研究低频振荡现象影响不大，可将牵引逆变器和牵引电机进行合理简化，最终将HXD2B型机车等效为带电阻负载的脉冲整流器模型，具体等效电路如图7所示。图7中将车载变压器等效为理想电压源un，输入侧电流为in，Rn和Ln为归算到次边的车载变压器电阻和漏电感，L2和C2是直流滤波环节，Cd是支撑电容，Rd是等效负载阻抗，ud是输出直流电压。

图7 HXD2B机车网侧整流器等效电路

1.2.2 瞬态电流控制系统数学描述

HXD2B机车采用瞬态电流控制策略产生整流器PWM触发脉冲信号，如图8所示。整个控制系统由电压外环控制、电流内环控制、锁相环、正弦脉宽调制等模块组成。瞬态电流控制是在改进电压电流双闭环控制的基础上，结合前馈控制，实现牵引网侧电流跟踪电流给定值，脉冲整流器输出直流电压跟踪直流侧电压给定值。相比于传统双环控制，拥有结构简单、动态响应迅速、对控制器的负荷更小等优点。

图8 HXD2B机车网侧整流器瞬态电流控制框图

考虑电压外环、电流内环、滤波环节和采样延迟等环节，单台机车网侧变流器控制传递函数框图如图9所示。

图9 HXD2B机车网侧整流器控制传递函数框图

为便于稳定性分析，给出HXD2B机车主电路的主要参数，见表2。

表2 HXD2B机车主电路参数

根据图3，车网级联系统主要包括牵引供电网等效阻抗Zo和电力机车负载等效阻抗Zin两部分。牵引供电网拓扑相对稳定，而电力机车部分由于车载脉冲整流器的脉冲宽度调制过程和数字控制时的采样延时都是非线性因素，所以车网级联系统实际是一个非线性时变系统。实际低频网压波动出现在几个电力机车同时整备或启动时，级联系统的时变性可不予考虑；针对系统非线性对车网级联系统稳定性分析影响，主要需对电力机车整流器数学描述进行线性化处理。针对本文考虑的HXD2B电力机车整流单元，采用小信号模型[19]，结合图9控制传递函数，通过瞬态电流直接控制求得整流器输入阻抗，可以建立相应的线性化模型，以进一步分析车网级联系统稳定性。

设车载变压器的变比为k，机车单个整流器输入阻抗折算到牵引网侧的输入阻抗Zin1为

( 6 )

设同一时间有n列HXD2B电力机车进行系统整备，则n列车的系统最终输入阻抗Zin=k2Zin1(s)/6n。基于以上推导，已完成该车网级联系统两大模块的数学描述，接下来对该车网级联系统进行稳定性分析。

2 车网级联系统稳定性分析

2.1 车网级联系统闭环传递函数

由图3可得到车网级联系统闭环传递函数为

( 7 )

式中:Zo(s)/Zin(s)=L(s)为系统开环传递函数，开环传递函数L(s)为

( 8 )

该系统传递函数只是一个关于s的表达式，所以整个车网级联系统可看作一个单输入单输出系统。根据现代控制理论，该系统稳定的充要条件是系统的Nyquist曲线在s域不包围点(-1，j0)。为了满足这一条件，Middlebrook[20]在Nyquist判据基础上，提出了基于实际阻抗的系统稳定性判据，若要保证级联系统稳定，系统在全频率范围内的输出阻抗Zo远小于负载输入阻抗Zin。

2.2 禁止区域与不可接受相位带

电气化铁路网侧低频电压波动往往引起牵引故障甚至牵引封锁。为了尽可能避免该情况，在系统稳定性分析中采用相对保守的稳定性分析方法更为可靠。基于Middlebrook判据，考虑系统相角因素，Wildrick划定了系统极坐标图的禁止区域[21]，提出基于阻抗的改进判据，该判据可对车网级联系统进行稳定性分析中实现输出阻抗Zo和负载输入阻抗Zin解耦，该判据禁止区域如图10所示。

图10 禁止区域示意图

在图10中，对应的禁止区域数学描述为

|Zo|-|Zin|>-GM

( 9 )

180°-PM1<∠Zo-∠Zin<180°+PM2

(10)

式中:GM为系统增益裕度,dB；PM1和PM2为系统相角裕度，(°)。考虑系统的临界稳定状态，在增益裕度GM取值上，文献[17]在未改进的考虑CRH5车型的系统稳定性分析中，采用GM=0 dB，本文基于更为保守的Middlebrook判据分析也采用GM=0 dB。为实现系统更为保守性分析，具体相角裕度取较小值PM1=PM2=5°，根据式(10)，在相位上可以得到车网级联系统稳定性分析中机车输入阻抗Zin的不可接受相位带，如图11所示。

图11 机车输入阻抗Zin不可接受相位带

依据图11，HXD2B型车网级联系统稳定性可直接从判据相位带角度来分析，进而可确定车网级联系统各个电气参数阈值。

(1)分别提取系统机车输入阻抗Zin与牵引网输出阻抗Zo，对两者波特图进行比较；

(2)当全频范围内|Zo|<|Zin|，车网级联系统稳定；

(3)当|Zo|≥|Zin|，则|Zo|与|Zin|存在交叠区域，进一步考虑Zo与Zin相位关系，在交叠区域对应的频率范围内，如果Zin的对数相频特性曲线进入了不可接受相位带，系统不稳定，反之系统稳定。

2.3 Zo恒定且Zin变化的车网系统稳定性

根据车网级联系统开环传递函数式( 8 )，当系统牵引网输出阻抗Zo恒定时，机车负载输入阻抗Zin会影响系统稳定性。负载侧阻抗Zin主要由机车数n、整流器电流内环采样周期Ti和电流内环控制函数Gi(s)几个参数确定。

2.3.1 不同的机车整备数量n

低频网压振荡大都发生在多车整备时间，首先分析并行机车数对车网级联系统稳定性的影响。增加不同整备机车机车数量，得到车网级联系统中4辆机车整备时Zin和Zo的波特图如图12所示。

从图12(a)可以看出，当n=4时，在对数幅频特性图中，当系统频率小于150.9 rad/s时，|Zin|>|Zo|；当系统频率处于150.9～1 969 rad/s时，|Zin|<|Zo|；当系统频率大于1 969 rad/s时，|Zin|>|Zo|。在全频范围内，|Zin|与|Zo|存在交叠区间，根据禁止区域原理， 不能直接由Zo和Zin的对数幅频特性曲线来确定系统稳定性，需考虑两者对数相频特性关系。在对数相频特性图中，Zin在148.3 rad/s之前位于不可接受相位带，在148.3～1 969 rad/s时，包括|Zin|与|Zo|交叠区间，Zin对数相频特性曲线已脱离不可接受相位带，根据禁止区域原理，车网级联系统保持稳定。

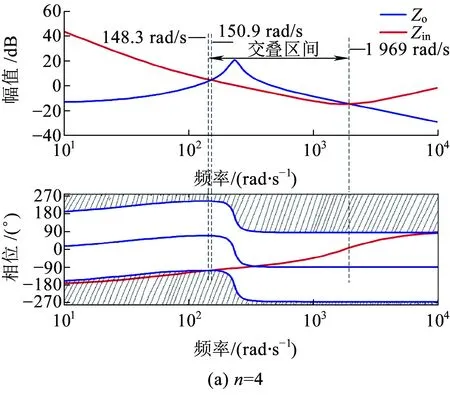
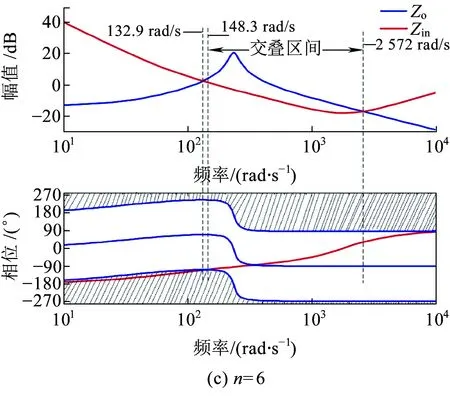
图12 不同机车整备数量n时的车网系统稳定性

从图12(b)可以看出，当n=5时，在对数幅频特性图中，当系统频率小于141 rad/s时，|Zin|>|Zo|；当系统频率处于141～2 294 rad/s时，|Zin|<|Zo|；当系统频率大于2 294 rad/s时，|Zin|>|Zo|。即在全频率范围内，|Zin|和|Zo|存在交叠区间。考虑对数相频特性图，Zin在148.3 rad/s之前位于不可接受相位带，在141～2 294 rad/s之间，Zin有7.3 rad/s进入不可接受相位带，此时车网级联系统不稳定。

从图12(c)可以看出，当n=6时，在全频率范围内，|Zin|和|Zo|存在交叠区间，系统稳定性不能直接由对数幅频特性曲线来确定；考虑对数相频特性，Zin在148.3 rad/s之前位于不可接受相位带，而在148.3～2 572 rad/s之间，Zin有15.4 rad/s进入不可接受相位带，车网级联系统不稳定。

从图12可以看出，随着车网级联系统中整备机车数量的增加，系统会由稳定状态过渡到不稳定状态；而且随着n的增加，Zin进入不可接受相位带的频率范围也在增加，表明车网级联系统的不稳定程度也在随着列车数的增加而增大。

图12中，不断改变n的数值，当出现|Zin|、|Zo|交叠区间起始频率与Zin进入不可接受相位带起始频率相等时，此时n值即为系统处于临界稳定时的投入系统机车数量最大值(求得n<4.24)。由此得到相对保守性的分析结果，该车网级联系统投入4辆HXD2B机车时系统处于稳定状态；当车网级联系统投入5辆和大于5辆HXD2B机车时系统不稳定。

2.3.2 不同的整流器电流内环电流采样周期Ti

接下来分析机车整流器控制参数对于车网级联系统稳定性的影响。针对电流内环电流采样周期Ti，改变整流器采样时间，从Ti=0.000 1～0.000 4 s，每次增加0.000 1 s，得到Zin与Zo的波特图，如图13所示。

图13 不同Ti时的车网系统稳定性(Ti=0.000 1～0.000 4 s)

从图13可以看出，从Ti=0.000 1～0.000 4 s，|Zin|与|Zo|的交叠区间频率(rad/s)依次为[179.8，435.6]、[151.1，1 860.2]、[133.3，2 590.1]和[120.6，2 747.2)。显然在各交叠区间终止点，Zin的对数相频特性曲线并没有进入不可接受相位带，所以仅需比较Zin与Zo开始进入交叠区间时Zin的对数相频特性曲线。

4种工况下，Zin分别于145.9、147.2、148.3和149.5 rad/s开始脱离不可接受相位带，即在|Zin|与|Zo|交叠区间内，Zin的对数相频特性曲线分别有-33.9，-3.9，15，28.9 rad/s进入不可接受相位带。在Ti=0.000 1 s和Ti=0.000 2 s时，车网系统稳定，当Ti=0.000 3 s和Ti=0.000 4 s时系统不稳定，车网系统不稳定程度随着Ti增大而增强。

当其他参数不变时，若交叠区间起始点频率等于Zin进入不可接受相位带的起始点频率，得到使车网级联系统稳定的Ti的取值范围为Ti<0.000 22 s。

2.3.3 不同的电流内环电流控制器Gi(s)

文献[22]指出，当忽略网侧寄生阻抗时，电流内环采用PI控制器的性能与采用比例P控制器的性能相同，因此在系统稳定性分析中，针对电流内环控制函数Gi(s)=KPI+KII/s，可不讨论电流内环积分参数KII影响，主要考虑KPI的影响。取KPI=2.7～3.0，每次增加0.1，波特图如图14所示。

图14 不同KPI时的车网系统稳定性(KPI=2.7～3.0)

从图14可以看出，从KPi=2.7～3.0，|Zin|与|Zo|的交叠区间频率(rad/s)依次为[135.3，2 602]，[136.6，2 622]、[137.9，2 638]和[139.2，1 657]，4种工况下，Zin的对数相频特性曲线分别于144.7、142.2、139.9和137.8 rad/s开始脱离不可接受相位带。在|Zin|与|Zo|的交叠区间内，Zin的对数相频特性曲线分别有9.4、5.6、2、-1.4 rad/s进入不可接受相位带。在KPI为2.7时，车网系统稳定，当KPI为2.8～3时车网系统不稳定。

针对电流内环电流控制器Gi(s)的影响，如果增大电流内环比例控制参数KPI可以提高系统的稳定性。同理，若使系统稳定，应使KPI≥2.97。

2.4 Zin恒定且Zo变化的车网系统稳定性

牵引网作为车网级联系统的输电环节，对于车网级联系统稳定性也有影响，牵引网等效阻抗中电阻部分RS较小，牵引网分布电容C也比较小，而线路中电感值LS较大，构成牵引网等效阻抗主要部分。

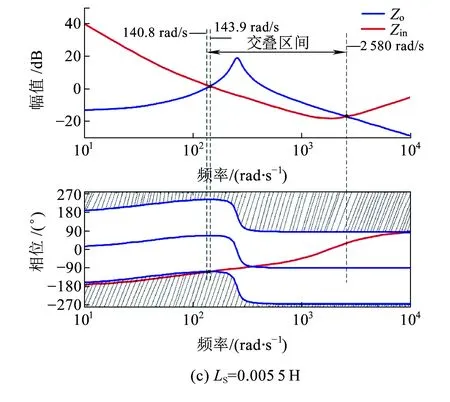
图15 不同牵引网阻抗Zo时的车网系统稳定性

取牵引网电感LS=0.003 5～0.005 5 H，每次增加0.001 H，观察波特图变化。图15中，|Zin|与|Zo|分别在[177.5，2 580]、[157.8，2 583]和[143.9，2 580]存在交叠区间频率，而在对数相频特性图中，Zin分别于67.9、122.3和140.8 rad/s脱离不可接受相位带，各有-109.6、-35.5和-3.1 rad/s位于不可接受相位带。随着LS的增加，系统稳定性在不断减弱，说明减小LS能增强系统的稳定性。若使车网级联系统保守性稳定，LS取值范围为LS<0.005 6 H。

3 测试验证

根据前文推导结果建立车网级联系统仿真模型如图16所示，设置7台机车通过断路器B1～B7接入牵引网同一位置。控制断路器闭合模拟机车投入的过程，具体仿真参数见表1、表2。

图16 车网级联系统仿真

首先设置仿真在单车运行的状态下，脉冲整流器输入电压电流和直流侧电压波形如图17所示。测试结果表明，整流器直流侧电压动态响应时间约为0.3 s，稳态时直流侧电压保持3 775 V，纹波小于50 V。网侧电压波形良好，网测电流与电压同相位，单车仿真结果与文献[4]相同，说明仿真模型有效。

图17 单车投入车网级联系统测试结果

3.1 Zo恒定且Zin变化的系统稳定性测试

在图16中，通过开闭合不同断路器模拟多车逐列投入车网级联系统的网侧电压电流进行测试分析。图18为测试结果，可以看到，在0 s时同时闭合断路器B1～B4，4辆机车在相同位置整备运行的牵引网侧电压电流波形正常。此后，分别设置断路器B5、B6、B7在0.4、1.6、2.8 s闭合，模拟运行机车数量增加的过程，断路器闭合时间间隔1.2 s是为了避免上一列车接入后产生暂态过程对下一列车仿真结果产生影响。测试结果表明：第5列机车接入后，牵引网侧电压电流发生波动，但在1～1.5 s之间波动幅度不断减小，逐渐恢复稳定。可以说明此时车网系统已处于稳定与不稳定的临界状态。第6列机车接入后，系统电气量参数发生明显的低频电气量波动，系统失稳。第7列机车接入后，电气量波动幅值增加，车网级联系统完全不稳定。整体的仿真结果和前面级联系统稳定性分析的结果4辆车稳定和5辆车处于临界稳定的结论基本相同，差别在于稳定性阻抗判据保守型所致，同时图18测试中出现的低频网侧电压电流低频振荡波形也再现了图1中现场实测的波形。

图18 机车整备数量n变化的系统稳定性测试对比

当机车数的投入为临界稳定状态5辆时，继续测试前面系统稳定性分析中其他电气量变化对系统稳定性的影响。首先将所有机车整流器的采样周期Ti由0.000 2 s变为0.000 4 s，其余参数保持不变。在0.4 s时闭合断路器B5接入第5台机车进行仿真，具体结果如图19所示。

图19 不同Ti时的车网系统稳定性测试

根据图19测试结果，在5辆车投入的系统临界稳定状态下，当Ti=0.000 2 s时，网侧电压波形处于临界稳定状态，波形相对良好；当机车整流器采样周期Ti增大至0.000 4 s后，网侧电压明显产生波动，系统不稳定，该测试结果和前面稳定性分析中的车网级联系统稳定性分析的Ti<0.000 22 s结论一致。

同理，将所有机车电流内环比例控制参数KPI的值由2.7调至3.0，其余参数不变。在0.4 s时闭合断路器B5接入第五台机车进行仿真，结果如图20所示。

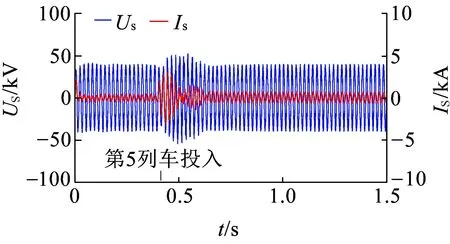
图20 KPI=3.0时的车网系统稳定性

由图20和图19(a)对比可以看出机车电流内环比例控制参数KPI=3.0时，牵引网侧电压电流波动在数周期后很快恢复完全稳定状态，波形更平滑，该结果和前面稳定性分析中使系统稳定KPI的取值范围为KPI≥2.97一致。

3.2 Zin恒定且Zo变化的系统稳定性仿真测试

保持机车仿真模型不变，将牵引网输出阻抗Zo中电抗部分LS减小至0.003 5 H，其余参数与图19(a)相同，测试对比结果如图21所示。

图21 牵引网阻抗LS=0.003 5 H时车网系统稳定性测试

图21与图19(a)对比，由于牵引网输出阻抗Zo减小而机车输入阻抗Zin未改变，车网级联系统仅在投入5辆车时小幅波动，但整个系统更加稳定，该结果和前面稳定性分析中使系统稳定LS的取值范围为LS<0.005 6 H一致。

通过仿真测试对比，可以看出接入机车数量增加会使系统稳定性下降，机车数量n=5时系统处于临界稳定状态；当接入机车数量一定时电流内环比例系数KPI和牵引网输出电抗LS对系统稳定性影响较大，适当增大KPI和减小LS可明显提高系统稳定性；而机车整流器采样周期Ti对系统稳定性影响较小，增大Ti会使系统稳定性降低。测试结果与本文稳定性理论分析结果一致。

4 结论

本文从稳定性分析角度深入分析了在徐州北牵引所多辆HXD2B型机车投入系统引发的低频振荡现象。推导了全并联AT牵引网和HXD2B型机车的等效电路，建立了车网级联系统的数学描述；将两个子系统级联后，获得车网级联系统的闭环传递函数；运用改进的基于阻抗的判据，对车网级联系统进行稳定性分析，从系统相位带角度，重点研究车网级联系统稳定性；通过仿真测试，验证了系统稳定性理论分析的有效性。并得出如下结论：

(1)针对机车等效输入阻抗的整备机车数量，同一供电臂下机车整备数量大于4时，系统开始不稳定。

(2)针对机车等效输入阻抗的机车整流器控制参数，发现机车整流器电流内环电流采样周期Ti对车网级联系统稳定性影响程度较大；电流内环控制函数中的积分参数KPI对系统稳定性影响较小，增大KPI能小幅度增加系统稳定性。

(3)针对系统的牵引网等效输出阻抗，减小牵引网等效阻抗有助于提高系统的整体稳定性。

总体来看，本文针对系统低频网压振荡稳定性分析的牵引网参数和整流器控制参数的调整与确定，在本质上都是为了实现两个子系统之间阻抗的相互匹配，进而可以实现车网级联系统的稳定性。