折叠方式对折叠翼气动及展开特性的影响*
2019-01-18单继祥龚志斌赵林东石运国
单继祥,龚志斌,赵林东,赵 平,石运国
(中国工程物理研究院 总体工程研究所,绵阳 621000)
0 引言
弹翼折叠可有效缩小外形尺寸、减轻结构重量,使其在箱式发射武器得到广泛应用。折叠翼可根据折叠方向分为横向折叠翼和纵向折叠翼[1-2]。横向折叠翼是在翼面根部或中部沿弹体轴向设置一分离面,安装转轴,在扭杆或扭簧的驱动力矩作用下,使折叠部分弹翼绕转轴展开。折叠翼能否迅速、安全、同步地展开是折叠翼设计的重要评判标准。折叠翼所受气动力对折叠翼展开时间、展开同步性均有重要影响,当折叠翼所受气动力超过一定程度时,甚至导致折叠翼无法展开到锁定位置,展开失败[3]。折叠方式是影响折叠翼气动力的重要因素,且对折叠翼的展开性能有重要影响。目前,针对折叠方式对折叠翼气动特性及其展开特性的研究很少,仅贾毅[4]通过地面试验比较了战术导弹折叠翼两种折叠方式的展开特性。
箱式发射导弹采用的横向折叠翼普遍采用折叠翼对称位于弹身左右两侧、上下对称折叠的折叠方式。针对该种折叠翼展开过程,国内外学者采用地面试验、动力学仿真等方法进行了大量研究。赵俊锋、崔二巍等[5-7]对折叠翼展开运动进行了动力学仿真,并对展开驱动力进行了优化设计。吴俊全[8]、甄文强[9]等对动力学计算结果及地面试验结果进行比较,并研究了折叠翼负载、摩擦力等参数对展开特性的影响。李真[10]采用CFD方法模拟了折叠翼展开的动态过程,研究了气动力对折叠翼展开特性及全弹姿态的影响。
针对常规折叠方式折叠翼,本文作者此前研究了不同位置折叠翼的气动特性,并分析了气动效应对折叠翼展开特性的影响[11]。在此基础上,本文设计了一种新型折叠方式,分析了两种折叠方式下折叠翼气动特性及展开特性,研究了折叠翼方式对其气动及展开性能的影响机制。
1 计算模型和方法
1.1 计算模型
本文采用的计算模型为弹身+ “×”型折叠弹翼模型,其外形如图1所示。本文研究了两种不同折叠方式下的折叠翼的气动及展开特性。

(a)展开状态 (b)对称折叠状态 (c)顺向折叠状态
图1(b)为第一种折叠方式,上侧折叠翼向下折叠,下侧折叠翼向上折叠,沿纵向及横向均对称分布,本文称之为对称折叠方式。图1(c)为第二种折叠翼方式,其左侧两片折叠翼逆时针折叠,右侧两片折叠翼顺时针折叠,对称分布于弹身两侧,本文称之为顺向折叠方式。两种折叠翼方式相比,上折叠翼位置完全相同,下折叠翼位置则相对于下固定翼对称。折叠状态下,固定弹翼与折叠弹翼之间的夹角为45°,两者间的夹角随翼面的展开而增大,直至折叠翼完全展开到位,如图1(a)所示。
1.2 数值计算方法
在折叠翼气动特性模拟方面,控制方程采用基于雷诺平均方法的三维N-S方程,如式(1)所示:
(1)
式中Q为守恒量;F、G、H为无粘矢通量;Fv、Gv、Hv为粘性矢通量。
流场求解器采用的是基于三维结构网格的有限体积求解器,粘性项采用James中心差分,无粘项采用Roe格式。湍流模型采用Menter提出的两方程k-ωSST模型。
1.3 折叠翼展开动力学仿真
展开过程中,折叠翼受到包括气动力矩在内的多种力矩作用,且部分作用力矩的大小与折叠翼展开角度相关。针对本文的计算模型,折叠翼在展开过程中主要受扭杆驱动力、惯性力、摩擦力及气动力等的作用。
根据文献[9],折叠翼展开的动力学方程如式(2)所示:
θw)+M1+Mf=0
(2)
1.4 计算方法验证
本文对某全弹模型气动力数值计算和试验结果进行了比较,以研究数值计算方法的正确性和网格的可靠性。图2是不同弹翼状态下,全弹气动力计算和风洞试验曲线。由两者比较可看出,弹翼折叠、展开状态下,全弹各纵向气动力系数计算与试验曲线基本吻合,表明本文采用的数值模拟方法及计算网格对折叠翼气动特性的模拟结果是可信的。

(a)CD-α (b)CL-α (c)Cm-α
单片折叠翼展开角度的动力学仿真结果与试验结果如图3所示。从图3中可看出,折叠翼展开角速度变化曲线与试验结果吻合较好,采用本文的动力学仿真方法可较准确地模拟折叠翼的展开特性。

图3 折叠翼展开运动过程计算与试验结果比较
2 计算结果与分析
2.1 折叠方式对折叠翼气动特性影响
本文首先对不同展开角度下对称折叠、顺向折叠时折叠翼的气动特性进行了数值模拟计算。由于折叠翼所受的气动力中主要是法向力及其产生的扭矩对折叠翼的展开起作用,所以本文主要分析了折叠方式对弹翼法向力、扭矩的影响。法向力系数、扭矩系数的定义方式同文献[11]。
图4、图5分别是当v=40 m/s、侧滑角β=0°、各展开角度下,上下折叠弹翼气动力系数变化曲线。图中方式1是指对称折叠方式,方式2是指顺向折叠方式。由图4可看出,随攻角的增大,两种折叠方式下折叠翼法向力、扭矩系数均呈线性增大规律。除θ=135°外,相同展开角度下,顺向折叠方式时上折叠翼所受到的法向力、扭矩均大于对称折叠方式,且该规律随着攻角的增大愈加显著。这主要是由于与对称折叠时相比,顺向折叠时上翼面受到下翼面的下洗作用大幅减弱,使上翼面的气动效率提高,气动力系数增大,且该规律随着攻角的增大而更加显著。
由图5可看出,随攻角的增大,各折叠方式下下折叠翼法向力、扭矩系数均呈线性变化规律。相对状态下(即折叠翼方向与水平方向夹角相同时),除θ=135°外,顺向折叠时迎风侧折叠翼所受到的法向力大小与对称折叠时相比有所减小。这主要是由于顺向折叠时折叠翼与固定翼间的流动干扰相对于对称折叠翼时有所增强导致的。当α>0°时,与对称折叠时气动力作用方向随展开角度无变化不同,顺向折叠状态下,当展开角度大于一定程度后,折叠翼所受气动力反向。
总体而言,相对状态下,与对称折叠时相比,顺向折叠时下折叠翼所受气动力减小,上折叠翼略有增大。
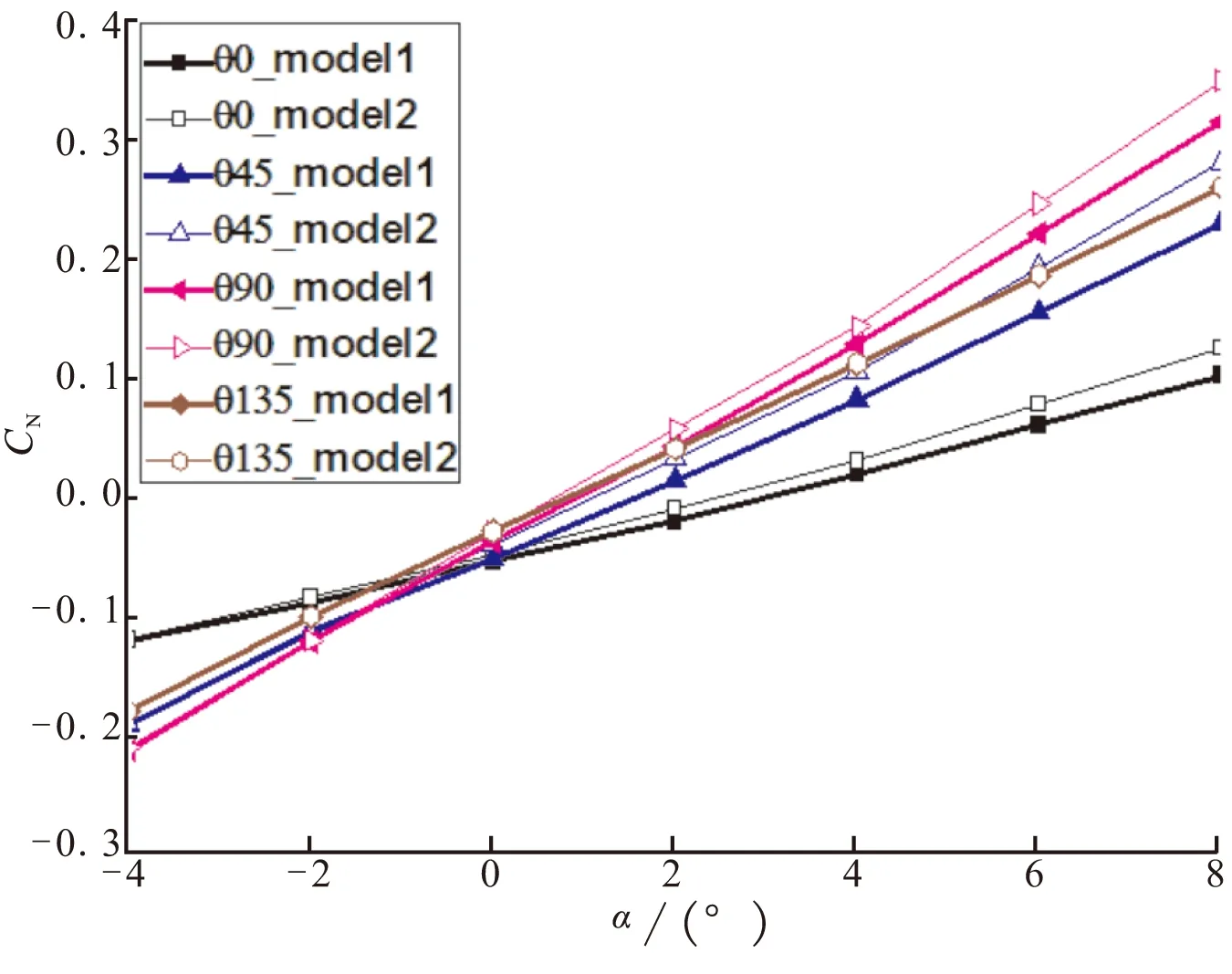
(a)法向力系数

(b)扭矩系数
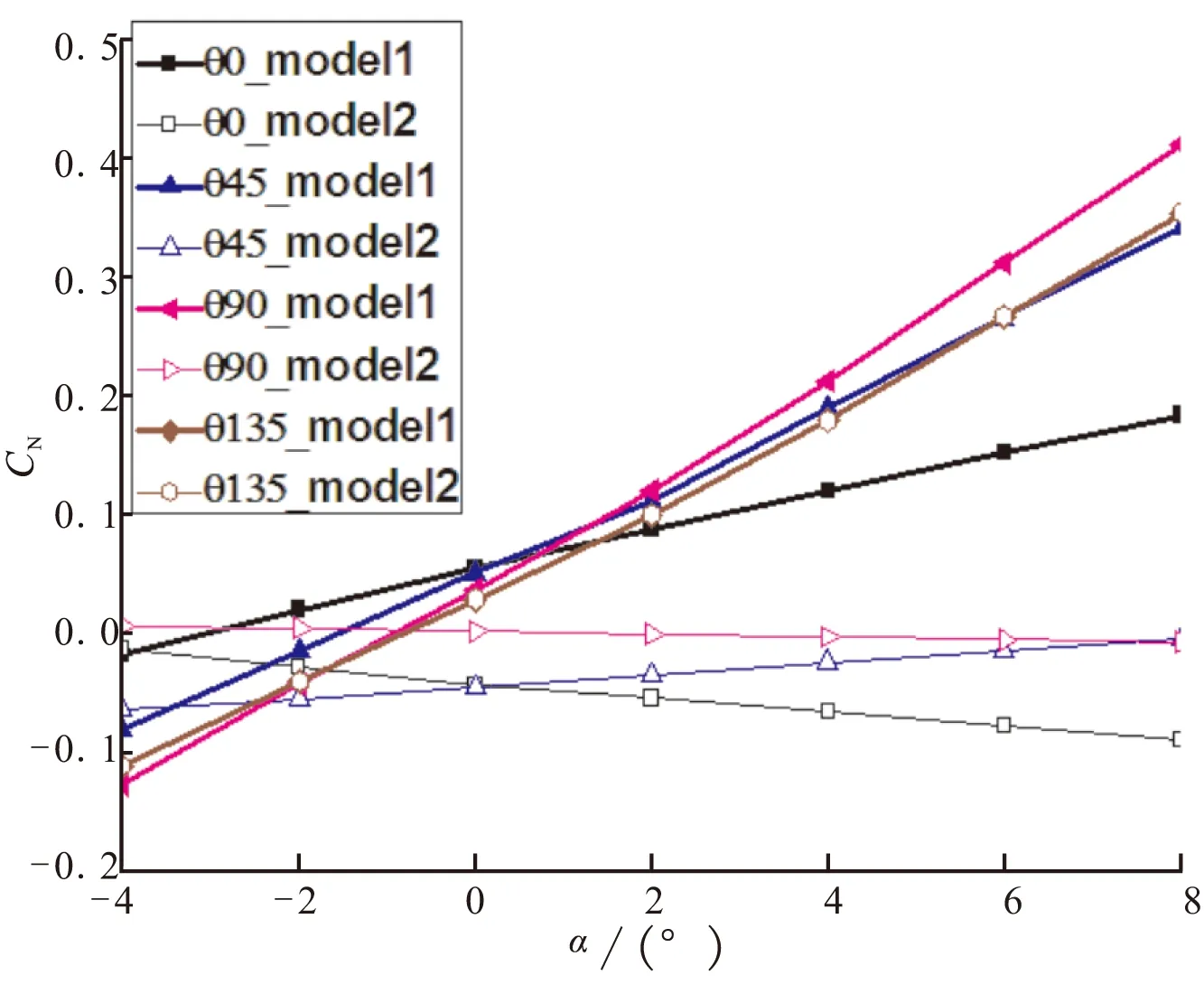
(a)法向力系数

(b)扭矩系数
2.2 折叠方式对折叠翼展开特性影响
无风条件下(理想状态),导弹或火箭弹在离箱后普遍以负攻角飞行。发射时的风干扰会诱导出附加攻角、附加侧滑角。因此,折叠翼的展开过程将面临较为复杂的气动载荷环境。本文对不同飞行状态下两种折叠方式弹翼展开运动过程进行了仿真,研究了折叠方式对折叠翼展开特性的影响规律。
图6、图7分别为当来流速度v=20~60 m/s、α=-4°和α=4°、β=0°时,上折叠翼、下折叠翼展开角度随时间的变化曲线。从图6可看出,对于上折叠翼,当α=4°时,与对称折叠时相比,顺向折叠时折叠翼展开时间有所减小,且随着速度的增大,减小幅度逐渐增大。当v=60 m/s时,顺向折叠上折叠翼展开时间缩短0.005 s,减少3%。当α=-4°时,两种折叠方式的上折叠翼展开曲线基本相同。但其中值得注意的是,负攻角状态下,气动力对上折叠翼的展开起阻碍作用,且该作用随着来流速度的增大而增强,导致展开时间明显增长。当v=60 m/s时,甚至出现折叠翼先展开后闭合,无法完全展开的现象。在折叠翼设计过程及折叠方式的研究中需重点关注。
对于下折叠翼,当α=-4°时,与对向折叠时相比,顺向折叠下折叠翼展开时间增大;当α=4°时,顺向折叠下折叠翼展开时间减小。同时,以上规律随着来流速度的增大进一步增强。当v=60 m/s时,顺向折叠时的下折叠翼展开时间由0.175 s缩短到0.153 s,减少了12.5%。
总之,与对向折叠时相比,顺向折叠主要是使下折叠翼展开时间减小,对上折叠翼展开时间基本无影响。由于折叠翼展开时间主要是由上折叠翼决定,所以两种折叠方式时,折叠翼展开时间基本一致。
折叠翼展开不同步是由上下折叠翼展开时间不同造成的。与对向折叠时相比,负攻角离架时,由于下折叠翼展开时间增加,导致折叠翼展开同步性增强;正攻角离架时,由于下折叠翼展开时间减少,导致折叠翼展开同步性减弱。
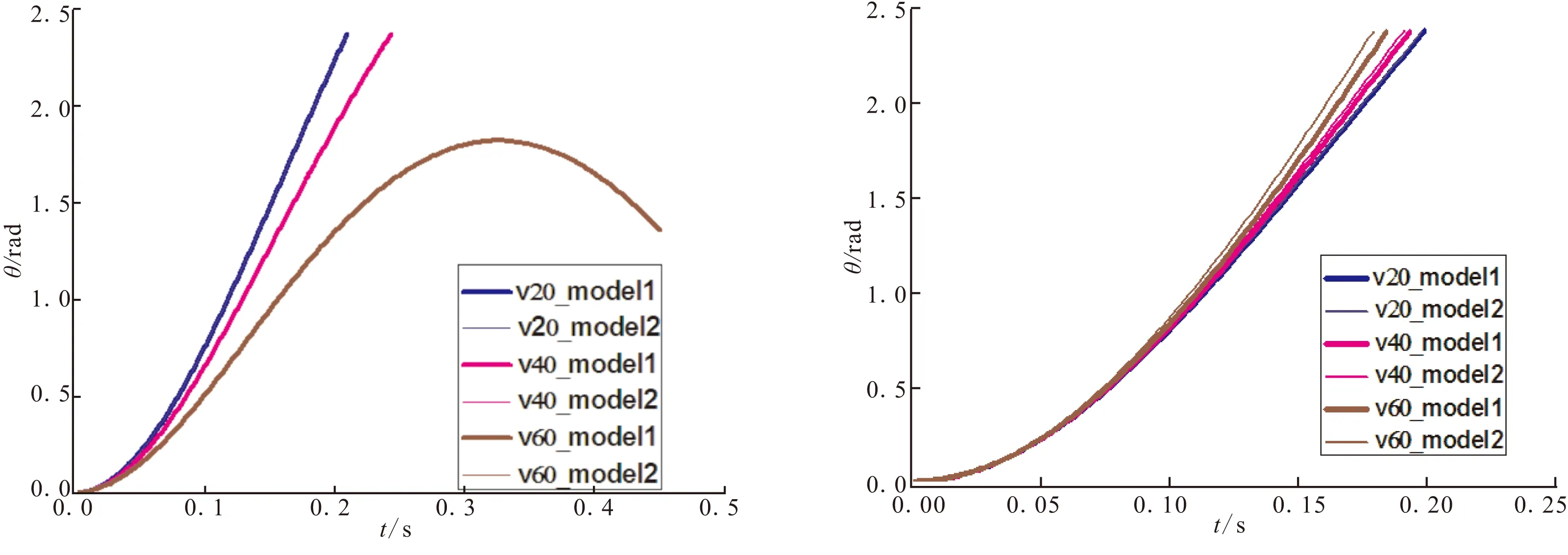
(a)α=-4° (b)α=4°
(a)α=-4° (b)α=4°
图8是当α=0°、β=4°、v=60 m/s时,不同折叠方式下的折叠翼展开角度曲线。由于4片折叠翼受到气动力、重力的影响各不相同,使得各折叠翼的展开运动过程也均不相同。与对称折叠时相比,顺向折叠时上翼面的展开特性基本相同,折叠方式对上翼面展开特性无影响;顺向折叠时,下翼面迎风侧折叠翼展开时间略有增大,背风侧折叠翼展开时间减小0.01 s左右。两种折叠方式折叠翼展开所需时间基本相当,顺向折叠时,折叠翼展开的同步性有所减弱。
2.3 折叠方式对全弹静稳定性影响
弹翼折叠将使弹翼有效面积减小,导致全弹静稳定性显著降低,甚至处于静不稳定状态,从而降低发射时的离架稳定性能。因此,本文分析了折叠方式对全弹的静稳定性的影响。
图9是当v=40 m/s、不同展开角度时,两种折叠方式下全弹的压心系数随攻角的变化曲线。从图9中可看出,与对称折叠时相比,当展开角度为0°时,顺向折叠方式下全弹的压心系数后移5%左右,全弹静稳定性提高;当展开角度θ=45°、90°时,顺向折叠时全弹的压心前移2%左右,稳定性有所降低,但由于此时全弹静稳定度已经较大,其影响较小。
由于折叠翼展开过程中,处于小展开角度状态的时间相对较长,采用顺向折叠的方式,可增强离架时全弹的静稳定性,改善发射时的离架性能。
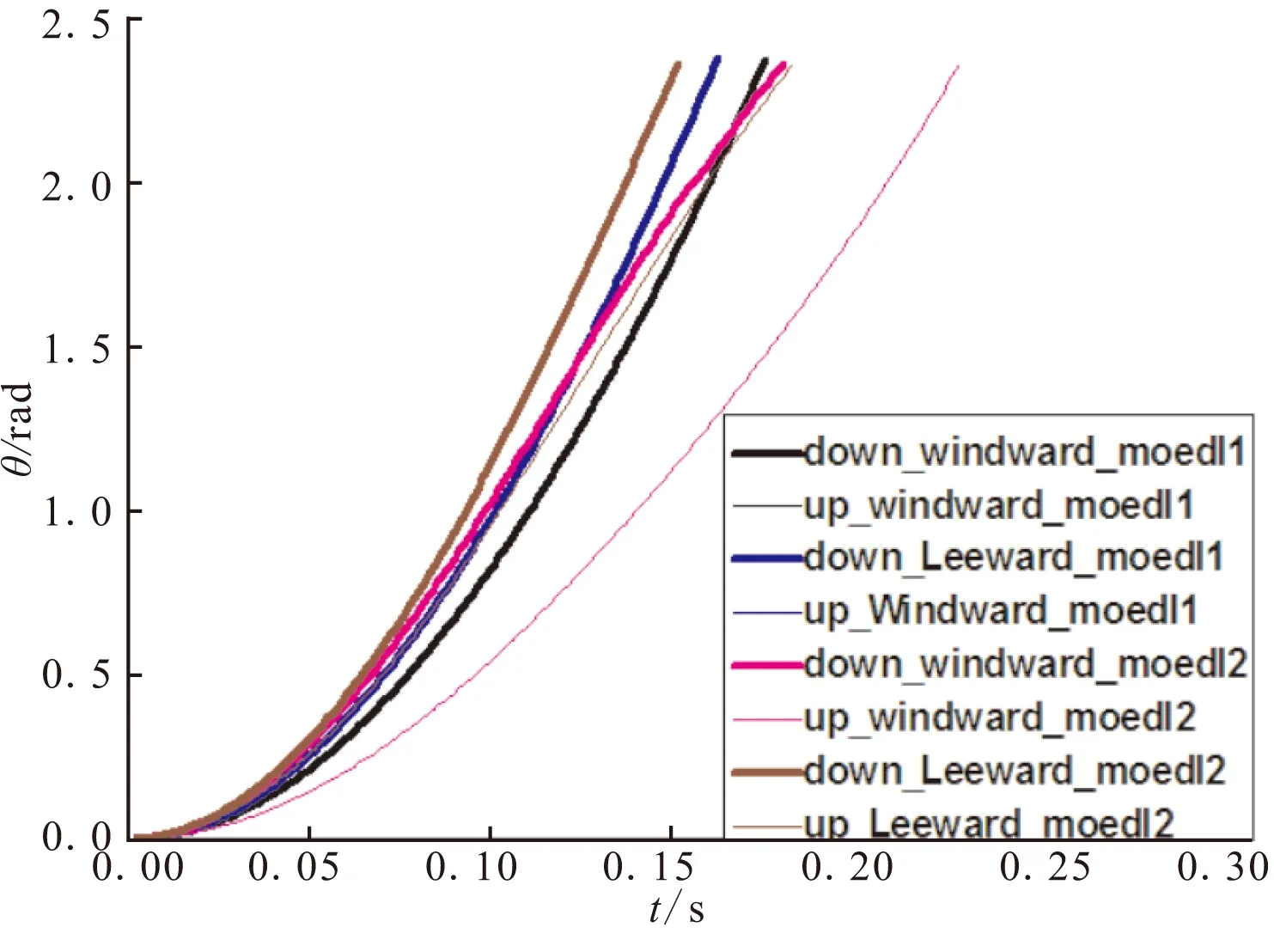
图8 不同折叠方式时折叠翼展开角度随时间的变化
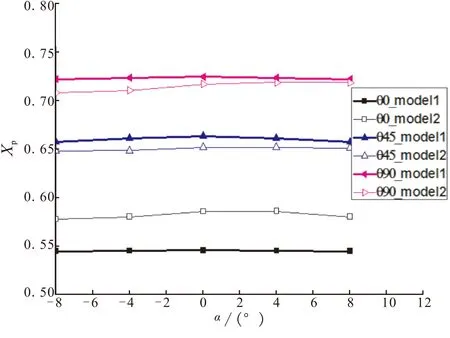
图9 不同折叠方式时全弹压心系数比较(v=40 m/s)
3 结论
(1)相对状态下,与对称折叠时相比,顺向折叠时下折叠翼所受气动力减小,上折叠翼气动力略有增大。
(2)与对向折叠时相比,负攻角时,顺向折叠时下折叠翼展开时间增加,同步性增强;正攻角时,下折叠翼展开时间减小,同步性减弱。
(3)侧滑状态下,两种折叠方式下折叠翼展开时间基本相当,由于背风侧下折叠翼展开时间减小,导致顺向折叠时折叠翼展开的同步性有所减弱。
(4)与对向折叠时相比,顺向折叠时,全弹的压心系数在小展开角度下后移,使全弹静稳定性提高,有利于提高导弹发射时的离架性能。
