ZrB2基超高温陶瓷热冲击模拟及失效分析①

王玲玲，张玉霞，王 琳，梁 军，方国东

(1.贵州大学 土木工程学院，贵阳 550025；2.哈尔滨工业大学 特种环境复合材料技术国防科技重点实验室，哈尔滨 150001)

0 引言

ZrB2基超高温陶瓷以抗高温、抗氧化及高强度的优势，成为飞行器结构关键部位的首选材料。但脆性大仍是该材料高温应用的技术难点，所以其抗热冲击性能研究至关重要。高温应用过程中，较大的温度差会使材料表面产生过大应力，导致材料或结构发生破坏甚至失效。因此，热防护材料的抗热冲击性能仍是高温应用过程中急待解决的难题[1-3]。

目前，材料抗热冲击性能的研究途径主要是借助实验测试、数值计算或理论分析。实验测试主要采用水淬方法，获得临界温差，以此来评价材料的抗热冲击性能。Zimmermann等[4]通过水淬实验获得ZrB2和ZrB2-30%SiC材料的临界温差均约为400 ℃，但ZrB2-30%SiC强度高，因此具有更好的抗热冲击性能。Kou等[5]采用水淬方法评估了机械冲击对陶瓷材料热冲击行为的影响。另外，通过水淬实验，可观察热冲击后试件表面的裂纹扩展情况，揭示陶瓷材料热冲击失效机理[6-7]。对于热冲击过程中材料的断裂失效以及裂纹的扩展情况，更适于应用数值方法[8-9]。理论分析主要以热损伤与热断裂理论为基础，分别采用材料断裂韧性与强度作为失效标准。两种准则适用范围不同，热断裂理论适用于材料内部预存在很短或很长的裂纹，热损伤理论适用于中间范围的裂纹尺寸[10-11]。

对于ZrB2基超高温陶瓷的抗热冲击问题，实验测试方面的研究成果较多，主要是结合水淬冲击和弯曲实验，确定临界温差，评价该材料的抗热冲击性能[12-13]。此外，热冲击过程中短时间内产生较大应力，具有冲击特性。所以，有些文献研究了惯性效应对材料抗热冲击性能的影响程度。Furukawa的研究[14]认为热冲击过程产生高速变形，会出现较大的应变率，针对厚板的热冲击问题，采用分离变量法求解出热应力，与静态情况相比，动态热应力以静态热应力为中心上下波动，数值上变化较小，惯性效应影响较小。Jeong[15]也提出可采用准静态强度值来评价材料的抗热冲击性能。刘国仟等[16-17]借助实验获得惯性应力随应变率的变化规律，通过叠加静态热应力与惯性应力来计算动态热应力，最大值约为静态热应力的2倍。Li等[18]指出裂纹尺度在毫米级以上时，可忽略惯性效应对热冲击性能的影响。Wang等[19]的近期研究成果表明，冷却速率对ZrB2基超高温陶瓷材料的抗冲击性能及断裂行为影响显著。显然，惯性效应及温度变化速率对材料热冲击的影响还需深入研究，且相关的动态失效判断准则较少。

综上所述，在ZrB2基超高温陶瓷材料热冲击性能分析中，惯性项影响程度评估与失效准则建立是亟需开展的重点研究内容。本文针对ZrB2基超高温陶瓷热冲击问题，基于热弹性理论，获得考虑惯性项和耦合项的动态热应力方程；根据实验试件形状与条件，建立相应的有限元模型，分析冷却与加热条件下该材料的热冲击行为，讨论惯性效应与耦合项对不同表面换热系数下材料热应力的影响；并结合动态实验结果评价该材料的抗热冲击性能，提出适用的失效准则，预测材料表面换热系数。

1 动态热弹性方程

基于热力学定律，热弹体问题中各向异性材料的热传导方程[20]为

(1)

式中βij为热力系数；cγ为材料的比热容；λij为材料的热导率。

对于固体的热弹性问题，变形较小时可认为应变与位移存在如下关系

γij=(ui,j+uj,i)/2

(2)

则本构方程可表达为

σij=cijmn(um,n+un,m)/2-βijT

(3)

动力方程为

cijmnum,nj+ρ0fi-βijT=ρ0üj

(4)

对于各向同性的均质体，应力、应变与温度的本构方程为

σij=λuk,kδij+μ(ui,j+uj,i)-βTδij

(5)

热弹性运动方程为

ui,jj+uj,ji/(1-2ν)+ρ0fi/μ-

2(1+ν)αT,i/(1-2ν)=ρ0üi/μ

(6)

若温度场变化较小，说明加速度üi较小，可忽略方程式(6)右侧的动力项(ρ0üi)，得到准静态热弹性方程。

ui,jj+uj,ji/(1-2ν)+ρ0fi/μ-

2(1+ν)αT,i/(1-2ν)=0

(7)

水淬实验环境，可看作第三类边界条件，表达如下：

(8)

式中h为对流换热系数；TA为介质温度。

2 有限元模型及边界条件

水淬实验获得的ZrB2-SiC-G材料临界温差约为400 ℃[21-22]，水淬试件为长方体条状试件，几何尺寸为36 mm×4 mm×3 mm，取四分之一几何模型建立热冲击试件的有限元模型，如图1所示。

本文选用的冷却条件：试件初始温度T0=400 ℃，外界温度TA=23 ℃。加热条件：初始温度T0=23 ℃，外界温度TA=800 ℃。热传导第三类边界条件中，表面换热系数可反映材料表面传热速率的大小，该系数影响模型温度场分布，同时也会影响材料的热冲击行为与失效机理。为研究表面换热系数对ZrB2基超高温陶瓷热冲击行为的影响，本文中表面换热系数取值分别为2×106、5×105、2×105、1×105、5×104、2×104W/(m2·K)。1000 ℃以下，ZrB2-SiC-G超高温陶瓷的力学行为表现为线弹性[23]。

采用ABAQUS有限元软件中Static Explicit、Dynamic Explicit及Dynamic thermal-mechanical coupling分析步，分别计算加热与冷却条件下ZrB2-SiC-G动态与静态热应力，研究惯性项与耦合项的对热冲击问题的影响程度。ZrB2-SiC-G超高温陶瓷材料的热学参数见表1。800 ℃以下ZrB2-SiC-G材料的拉伸模量310 GPa，室温与800 ℃时该材料的拉伸强度分别为146.7 MPa和122.7 MPa，泊松比为0.14。

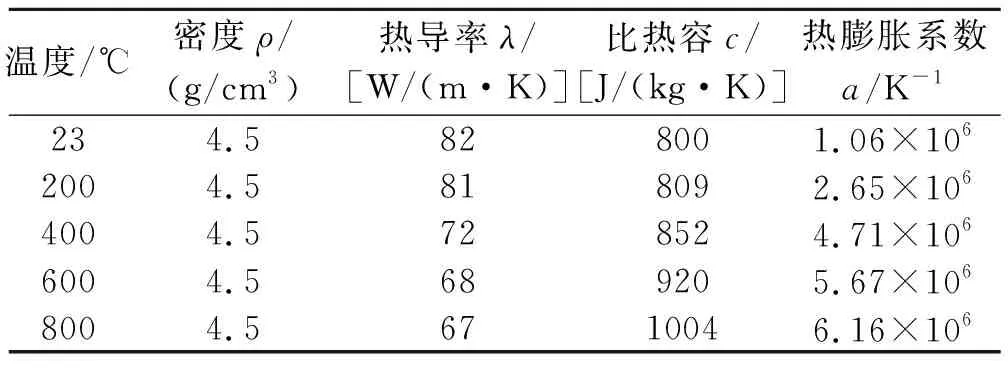
表1 ZrB2-SiC-G材料的热学参数

3 模拟结果及分析

3.1 冷却条件

不同表面换热系数下ZrB2-SiC-G超高温陶瓷最大热应力随时间的变化规律如图2所示。由图2结果可知耦合项对ZrB2-SiC-graphite材料热应力影响较小，可忽略不计。图2表明冷却时，ZrB2-SiC-G超高温陶瓷的动态热应力以静态热应力值为中心，上下波动。表面换热系数降低时，动态热应力的波动幅度随之减弱，当表面换热系数取2×104W/(m2·K)时，动态热应力与静态接近，此时惯性项对ZrB2-SiC-G超高温陶瓷热冲击行为的影响可忽略。不同表面换热系数下，试件动态、静态热应力最大值及达到最大值所需的临界时间如图3所示。表面换热系数越大，动态与静态热应力最大值之间的差值越大，表面换热系数大于1×106W/(m2·K)后，动态与静态热应力最大值比值趋于一固定值，约为1.21。

(a)h=2×106 W/(m2·K) (b)h=5×105 W/(m2·K)

(c)h=2×105 W/(m2·K) (d)h=1×105 W/(m2·K)

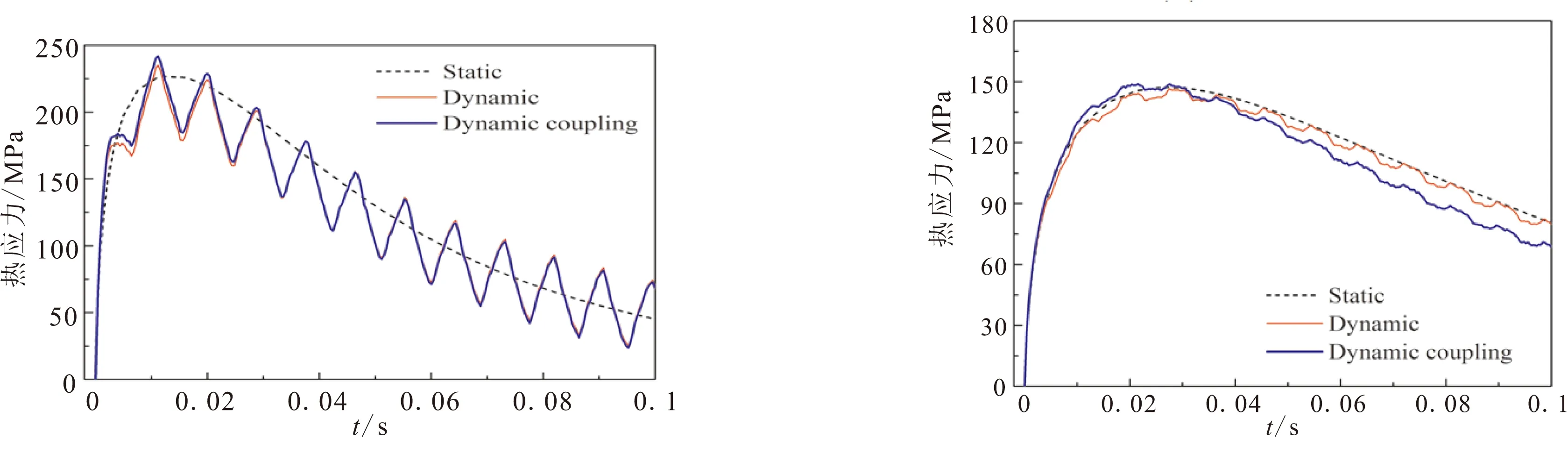
(e)h=5×104 W/(m2·K) (f)h=2×104 W/(m2·K)

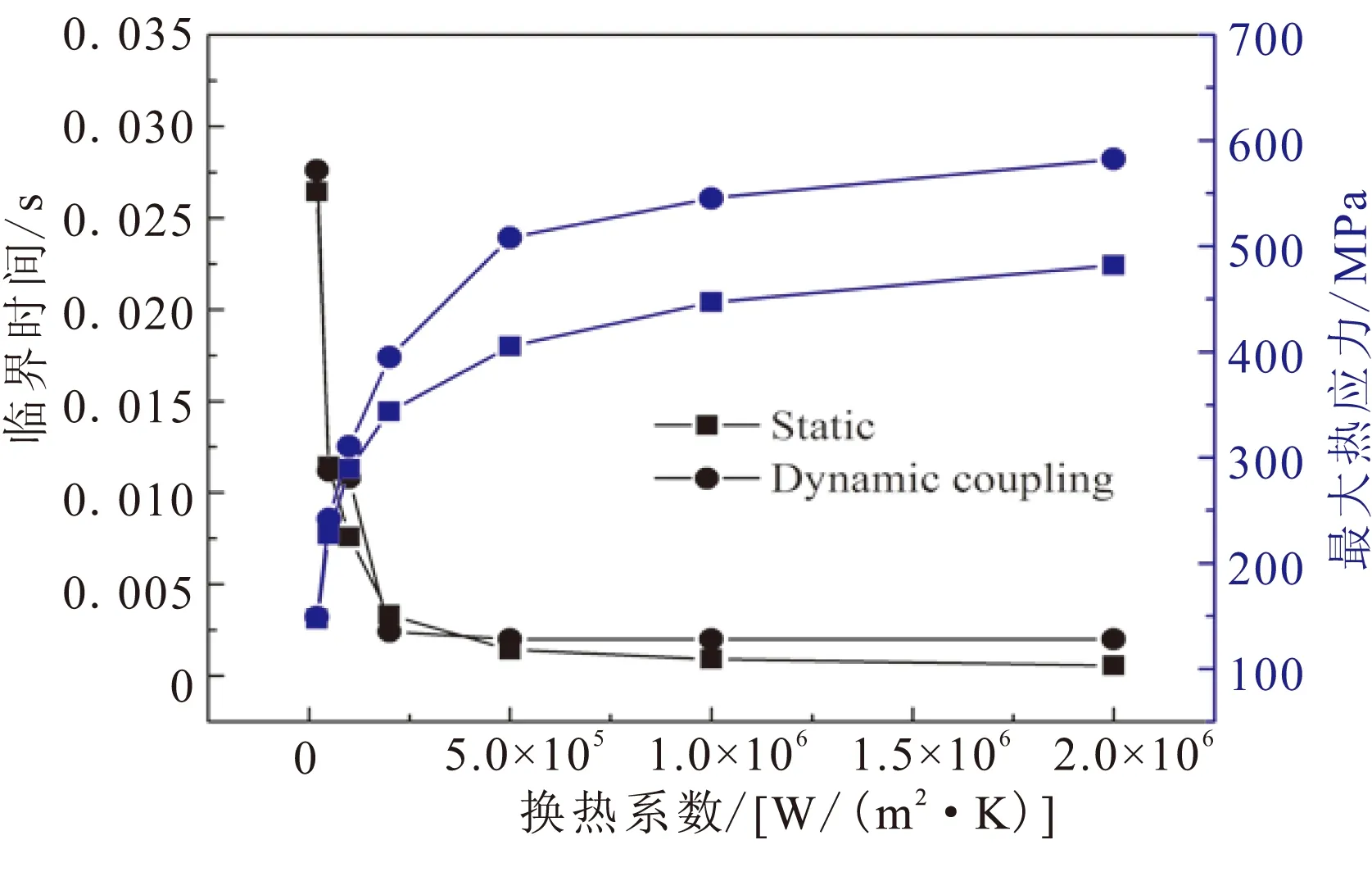
图3 不同表面换热系数下最大热应力与临界时间变化规律

3.2 加热条件

加热条件下，结构内部产生拉应力，表面产生压应力。图4为最大拉应力与最大压应力随时间的变化规律。无论拉应力，还是压应力，动态热应力均以静态值为中心上下波动。当表面换热系数小于1×105W/(m2·K)时，惯性项的影响可忽略不计，此时可用静态问题来研究ZrB2-SiC-G超高温陶瓷的热冲击行为。

由图4可知，加热条件下压应力最大值明显大于拉应力最大值，但ZrB2-SiC-G超高温陶瓷为脆性材料，压缩强度(907.6 MPa)远高于拉伸强度。表面换热系数相同的情况下，仍是拉应力先达到拉伸强度。所以，加热冲击下ZrB2-SiC-G结构并不是受压破坏，而是由拉应力过大导致失效。

(a)h=2×106 W/(m2·K) (b)h=1×106 W/(m2·K)

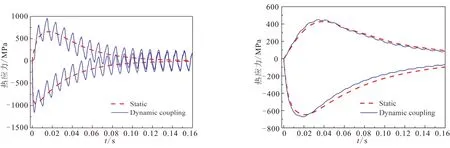
(c)h=5×105 W/(m2·K) (d)h=1×105 W/(m2·K)

最大拉、压应力及达到最大值所需的临界时间随表面换热系数变化规律如图5所示。表面换热系数越大，最大应力越大，临界时间越短，当表面换热系数超过1×106W/(m2·K)后，最大应力与临界时间的变化缓慢。表面换热系数相同时，最大动态与静态拉应力比值高于动、静态最大压应力比值。所以，加热时惯性项对拉应力的影响偏大，对压应力的影响弱之，表面换热系数越小，比值越小。

当表面换热系数大于1×106W/(m2·K)时，动态与静态最大拉应力比值约为1.33，表面换热系数取2×104W/(m2·K)时，比值接近于1.0，惯性项的影响可忽略。但在加热条件下，ZrB2-SiC-G超高温陶材料热冲击失效判据应采用拉伸强度。

3.3 热冲击失效分析

文献[24]结果表明，应变率对ZrB2-SiC-G复合材料强度影响明显，应变率不断升高，材料强度逐渐增大，尤其是超过临界应变率后，强度明显增大。因此应采用动态失效准则来评价该材料的热冲击性能。ZrB2-SiC-G的动态压缩强度与最大热应力随临界破坏时间的变化情况如图6所示。

动态压缩强度随临界破坏时间的增大而逐渐降低，在100 μs后，动态压缩强度可近似于静态压缩强度。整理出热冲击过程中，最大热应力与临界时间的变化关系，与动态实验结果对比，若最大应力超过相同临界时间时的动态强度，则表示材料失效。在加热冲击条件下，最小的临界破坏时间为1700 μs，远大于100 μs，此时材料动态强度近似为静态强度，此时可采用静态强度作为评价ZrB2-SiC-G材料热冲击失效的标准。根据热断裂理论，400 ℃水淬条件下，所采用ZrB2-SiC-G的静态拉伸强度(146.7 MPa)为失效指标，该材料表面换热系数约为2×104W/(m2·K)。

Becher等[25]提出水淬条件下临界温差的经验公式，如式(9)：

(9)

式中A为试件几何形状因子。

针对ZrB2-SiC-G材料水淬实验条件，本文取A=4，a=3 mm。σ为拉伸强度，在室温至800 ℃间按照线性插值计算，弹性模量E=310 GPa，泊松比υ=0.14，热导率λ与热膨胀系数α取值见表1。当临界温差为400 ℃时，采用式(9)计算得表面换热系数为1.3×104W/(m2·K)，与本文预测结果(2×104W/(m2·K))接近，验证了文中表面换热系数预测方法的正确性。

由式(9)可知，实验条件一定的情况下，材料表面换热系数的预测结果取决于强度。ZrB2基超高温陶瓷压缩强度约为拉伸强度的6倍，弯曲强度(400～500 MPa)居中。800 ℃加热冲击时，若以ZrB2-SiC-G材料静态压缩强度(907.6 MPa)为失效指标，预测出该材料表面换热系数约为3×105W/(m2·K)。但动态热冲击数值计算结果显示，无论加热还是冷却条件，ZrB2-SiC-G材料均由拉应力过大导致破坏，应以拉伸强度(146.7 MPa)为失效指标，预测的材料表面换热系数约为2×104W/(m2·K)。因此，准确地揭示热冲击失效机理是预测表面换热系数的重要前提。

4 结论

(1) ZrB2-SiC-G材料热冲击过程中，惯性项对热应力的影响较大，耦合项影响较小。惯性项的影响程度与表面换热系数直接相关。表面换热系数越大，惯性项作用效果越明显。

(2) ZrB2-SiC-G材料的最大动态拉应力与静态比值约为1.33。

(3) 800 ℃加热及400 ℃冷却条件下，ZrB2-SiC-G材料均是由拉应力过大导致材料失效，通过热断裂理论评价抗热冲击性能时，应采用拉伸强度作为失效指标，预测的材料表面换热系数均约为2×104W/(m2·K)。