组合后通过平移或旋转实现密铺的凹五边形研究

郝四柱

(南京金陵中学仙林分校中学部 210000)

1 问题提出

据外媒报道，美国华盛顿大学研究团队近日发现了一种新的不规则凸五边形，相互组合后可完全铺满平面，不会出现重迭或空隙，是全球第15种能做到此效果的凸五边形(如图1).而距上次发现类似效果的凸五边形已时隔30年，这项发现相当于在数学领域中寻获了新原子粒子.[1]它们的方法是“把12个全等的该五边形组合成图2的形如海马状图形，然后把海马状组合图进行平移，形成图3的密铺图案.”

图1

图2

图3

所谓的平面密铺也就是镶嵌，即，用平面图形完全覆盖一个二维平面，而且图形之间没有重叠；其中，只用一种全等图形的密铺，我们称之为单密铺.众所周知，1.由全等的三角形单密铺可以铺满整个平面；2.由全等的四边形单密铺可以铺满整个平面(含凹四边形)；3.正五边形由于每个内角为108°，所以不能密铺整个平面.那么，其它的不规则五边形单密铺问题成为人们研究密铺的一个焦点.

由于人们对于凸五边形密铺研究有了一些成果，那么凹五边形呢？目前还不多.所以本文探讨凹五边形的单密铺问题：“只用一种全等凹五边形，形成一种组合图形，然后把组合图形通过平移或旋转实现平面密铺.”

2 凹五边形通过组合，得到基本组合图形，该基本图形可以通过平移实现密铺

笔者从已有的凸五边形密铺方法入手，进行凹五边形的密铺的对比研究，结合正多边形特点、黄金三角形特点以及几何图形的相关知识的研究，得出结论如下：

(1)具有两边平行的凹五边形，组合后的基本组合图进行平移实现密铺

基本图基本组合图密铺图第1种情况∠B+∠C=180°,∠A+∠ D+∠E =360°(其中内角∠E大于180°)

(2) 通过正多边形的结构分解获得的凹五边形；这类正多边形必须可以进行平移实现密铺，从而实现凹五边形的密铺

由于正方形和正六边形是简单而优美的图形；并且都可以通过平移获得整个平面的密铺，所以通过对于正方形、正六边形的研究获得能够密铺的凹五边形.①将正方形分割成4个全等的凹五边形.其密铺的图案如下第2种情况.②将正六边形分割成6个全等的凹五边形.其密铺图案如下第3种情况.

基本图基本组合图密铺图第2种情况∠A=90°,a=b,c=e,∠B+∠E=360°,∠C+∠D=90°(其中∠B大于180°)第3种情况∠A=60°,a=b,c=e,∠B+∠E=360°,∠C+∠D=120°(其中∠B大于180°)

(3) 内角均为36°倍数的凹五边形，组合后的基本组合图可以进行平移实现密铺[2]

第4种情况基本图基本组合图密铺图a=b=c=d=e,∠A=∠D= 36°,∠ABC=∠BCD=108°其中内角∠AED=252°

(4)四条边相等的凹五边形进行组合，组合后的基本图形可以进行平移实现密铺

(5)两边或三边相等的凹五边形组合，组合后的基本组合图可以进行平移实现密铺

基本图基本组合图密铺图第8种情况b=d,c=e,∠B+∠D=180°;(其中内角∠A大于180°,隐含条件是:∠A+∠C+∠E =360°)第9种情况b=c,d=e;∠B=∠D=90°;(其中内角∠A大于180°,隐含条件是∠A+∠C+∠E =360°)第10种情况a=b,c=d;∠A=60°,∠C=120°;(其中内角∠E大于180°,隐含条件∠B+∠D +∠E=360°)第11种情况a=d=e,b=c;∠B+∠D=180°,∠E=2∠B(其中内角∠A大于180°,隐含条件是:∠A+∠C +2∠B=360°)第12种情况d=2a=2e,∠B=∠E=90°,∠A=∠C(其中内角∠D大于180°,隐含条件是:∠D+2∠A=360°)

3 凹五边形通过组合，得到基本组合图形，该基本图形可以通过旋转实现密铺

(一)凹五边形组合后的基本组合图，能实现旋转密铺；这样的凹五边形必须符合什么条件

首先有角度上的特征：因为凹五边形旋转一周为360°；所以凹五边形至少有一个内角应该是360°的因数.由于360°的因数有很多，其中常见的有30°、36°、60°、72°、90°、120°.

从边长来说，用同一种凹五边形通过旋转实现平面密铺，还体现在边长上：因为该图形通过旋转实现平面密铺，必须有边重合，所以有相等的边长.特别地，如果五边均相等，那么这样的凹五边形更容易实现旋转密铺.

(二)组合后的基本组合图，能实现旋转的单密铺研究

(1)和黄金三角形联系的凹五边形

① 黄金凹五边形的组合方式的介绍

图4

如图4，是五边相等的凹五边形ABCDE，内角均为36°的整数倍，(a=b=c=d=e,∠A=∠D=36°，∠ABC=∠BCD=108°，其中内角∠AED=252°)；用这类五边形组合后，可以通过旋转的方法实现密铺(如图5).该五边形是如何进行组合然后进行旋转密铺的呢？在进行旋转密铺之前，我们介绍一下三个关键的组合方法(图6、图7、图8)；图6组合是把图4通过旋转和轴对称实现的，图7的右半部分(虚线部分)和左半部分成中心对称，这样图7能够形成一个整体.

图5

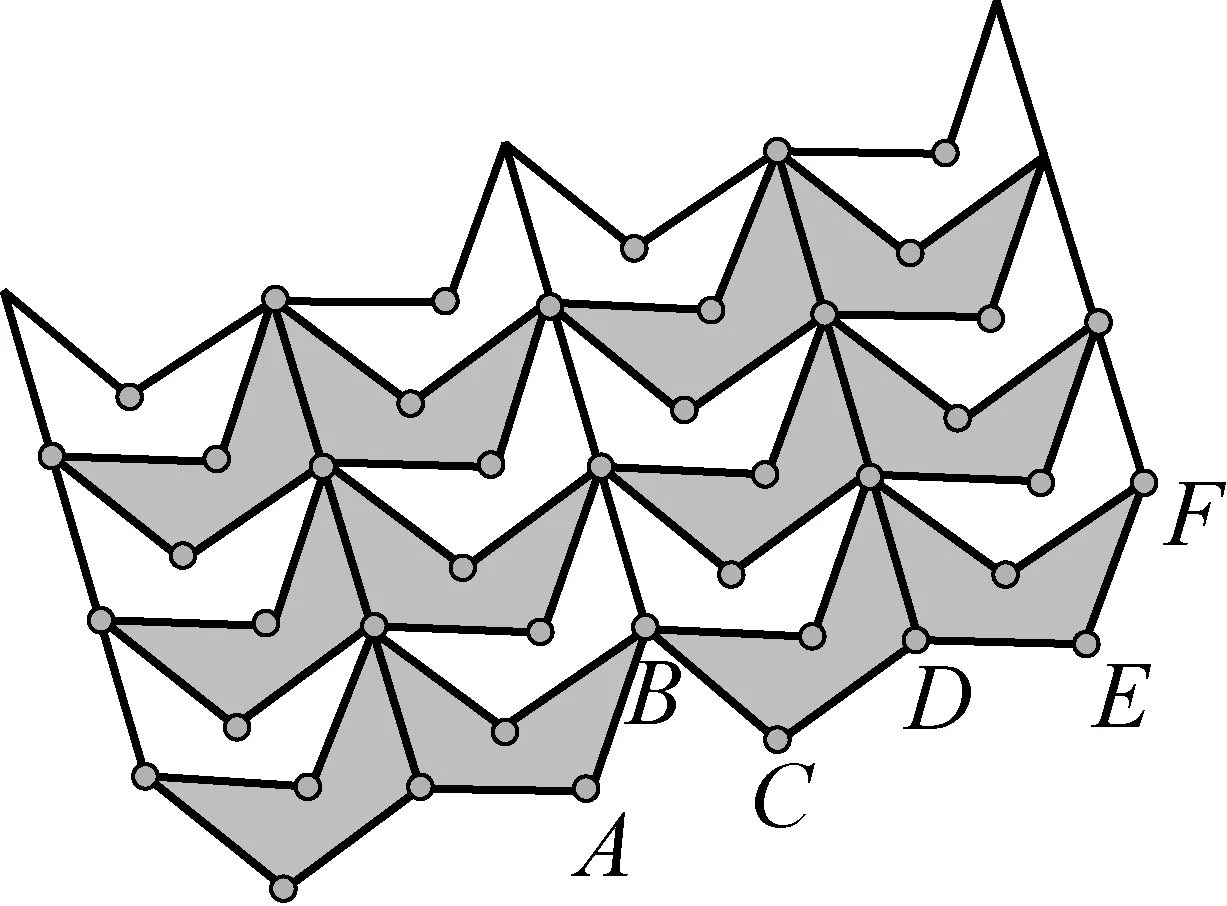
图6

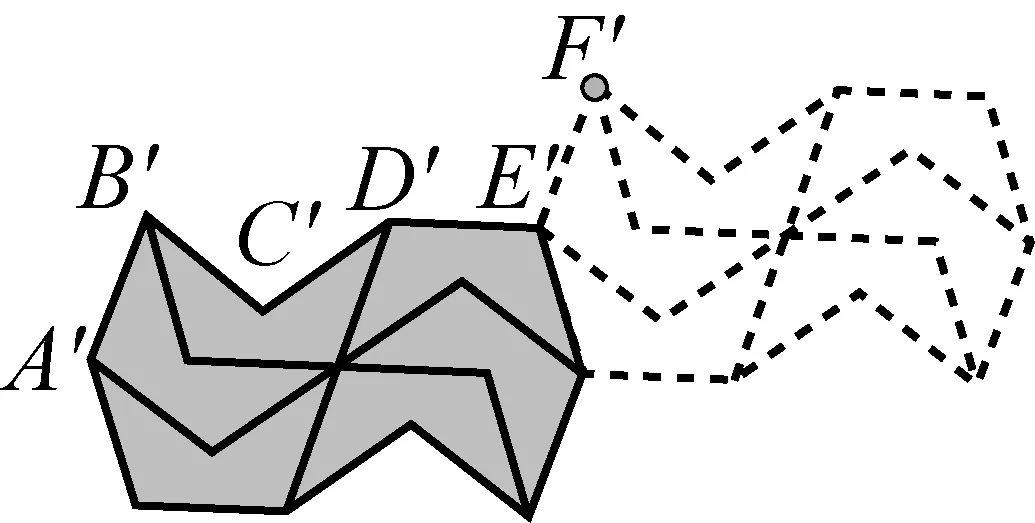
图7

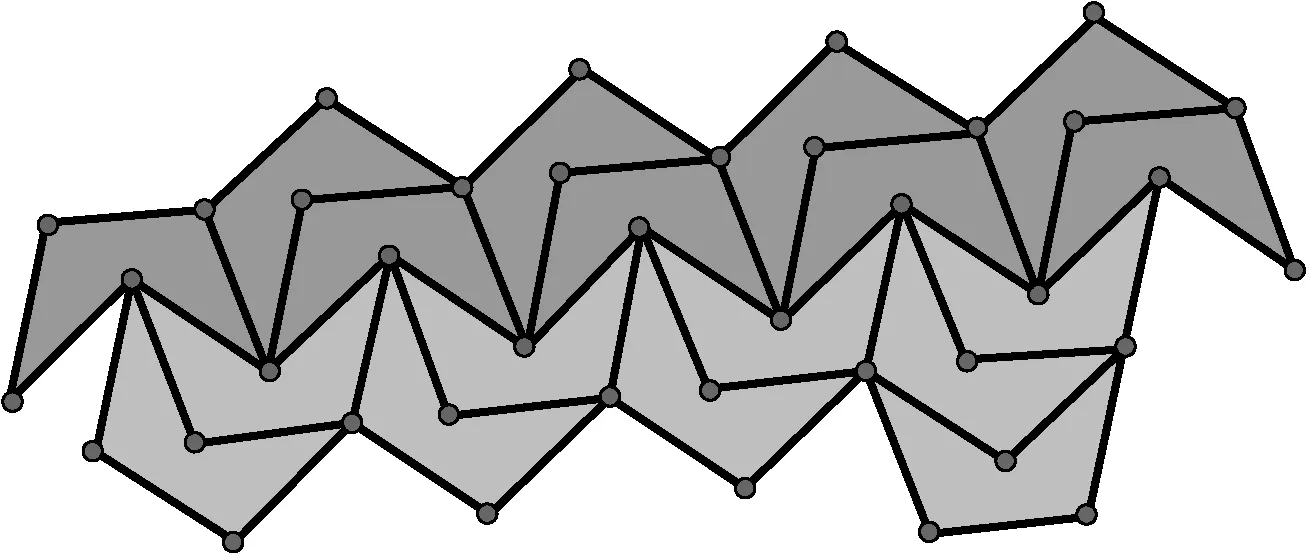
图8

另外，图6中下方的点A、B、C、D、E、F可以和图7中上方的对应点(A′、B′、C′、D′、E′、F′)正好可以进行咬合，实现图6和图7的边界线统一，圆满实现密铺(其中点B和点B′处对应的两个角度和正好是360°(一个为72°，一个为288°)；同样C和C′、D和D′、E和E′处均可进行咬合).

同时可以看到边界线B′C′D′E′F′构成对称的W型.为便于后面图形组合的描述，我们把图6和图7沿W型边界线密铺的方法称为咬合法.另外还有可能出现如图8的组合方法，该方法就是把两个相同组合，面对面扣起来.我们把这种方法叫做对扣法.对扣法中间出现一道W型的边界线.对扣法和咬合法均是这种凹五边形的组合方法，可以实现图5的密铺.

②图5的详细步骤见如下的(i)-(vi) 步骤

(i)基本框架(ii)向外按照图4的方法进行平移、不断延展(iii)将第(ii)步的延展部分旋转36°.(vi)继续将第(iii)步的部分进行旋转,每次36°,从而形成整个密铺的支架.(v)将十条延展图之间的空档用W型进行咬合和对扣(vi)将图形第(v)步每次旋转36°,旋转一周,实现整个平面的密铺

这里还需要强调说明的是上述的第(v)步，内部是如何密铺的呢？首先看一下第(iii)步中，“两条腿”边界都是连续的W型轮廓线，我们沿着(iii)的两条腿相对的W型轮廓线，用咬合法同时相向密铺，内部交汇处是采用对扣的方法，其相遇处是一条连续的W曲线，近似于角平分线.从而形成第(v)步的内部密铺.

(2)和30°、60°、90°相联系的凹五边形

图9

第二个凹五边形ABCDE，如图9，条件是：a=b=c=d=e,五个内角分别是：∠A=60°，∠ABC=210°，∠C=30°，∠D=150°，∠AED=90°,即,由等边三角形和一个角为30°的菱形组成基本图形.

该凹五边形同样可以通过旋转实现密铺方案如下(密铺方法见下表)：方案一，以该五边形的90度角的顶点为中心，90°旋转角进行旋转，得到正十二边形；方案二，以该五边形的60度角的顶点为中心，60°旋转角进行旋转，设计出两种图案，两层正十二边形的旋转密铺和三层的正十二边形的旋转密铺；方案三，以该五边形的30度角顶点为中心，30°角为旋转角来进行旋转，设计出四层正十二边形旋转密铺图案和五层的正十二边形的密铺图案(如下表).只要愿意，三种方案均可无限向外扩展，从而实现整个平面的密铺.

密铺图1密铺图2方案一:以90°角为旋转角实现旋转密铺方案二:以60°角为旋转角实现旋转密铺方案三:以30°角为旋转角实现旋转密铺.

我们不妨以方案三为例：以四层的正十二边形为基础，如何拼出五层正十二边形呢？进而达到更多层数的正十二边形？操作程序如下：

①构造正十二边形以方案三为基础②向外拓展所需要的一个组合图形:右图一的凹八边形,是向外密铺的一个基本构图方法.③向外拓展:右图二是将四层的正十二边形每个顶点处都增加的一个该凹八边形. ④上述两个凹八边形之间的空档需要填空,可用右图进行填空,从而得到相应的五层的正十二边形.⑤将上述①-④的方法不断的向外进行拓展,可以得到更多层数的正十二边形,实现整个平面的密铺.⑥艺术密铺:通过上述三种旋转方法,配上不同颜色,可以铺出五彩斑斓的花朵图案.

续表

综上所述：本文所述的凹五边形，组合后的基本组合通过平移或者旋转这两种变换实现密铺；对于其他未知的凹五边形研究可以起到启示作用.相信随着计算机和相关技术的进步，未来一定会有更多的能够实现密铺的的凹五边形被发现.