激活问题意识 点燃思维火花——以一道高考题的两个教学片段为例

顾日新

(苏州工业园区星海实验中学 215021)

1 问题提出

随着教育教学改革的不断深化，培养学生的创新能力作为一个核心问题被摆到重要位置．众所周知，创新能力的核心是创新思维，创新思维的动力是问题意识．问题意识最为显性的表现就是敢于提出问题、敢于质疑．爱因斯坦认为：“提出一个问题往往比解决一个问题更为重要，……”；《中国学生发展核心素养》一文中也明确指出：“善于发现和提出问题，有解决问题的兴趣和热情；……，是‘实践创新’素养的主要表现之一”．由此可见，激活学生的问题意识，事关创新思维、创新能力及核心素养．但是，学生的问题意识需要谁来激活？又该如何激活？本文以一道高考题的两个教学判断为例，在对比中寻求答案．不足之处，敬请同行批评指正．

2 教学实录

2.1 高考真题

2008年江苏高考数学第19题的第(1)小题：

设a1,a2,……,an是各项均不为零的等差数列(n≥4)，且公差d≠0，若将此数列删去某一项得到的数列(按原来的顺序)是等比数列：

2.2 教学背景

这是高一年级下学期学完《数列》一章的章节复习课，考虑到高一学生的学情，备课组内集体备课时删去了原高考题的第(2)小题，仅选用了第(1)小题作为例题．关于如何讲解这道例题，备课组内并没有进行探讨，两位执教老师自由发挥，同题异构．

2.3 教学片段

片段1

教师用PPT出示2008年江苏高考数学第19题的第(1)小题，在学生思考五分钟之后开始提问．

师：生1，请分享一下你的思路．

生1：n=4时，即a1,a2,a3，a4成等比数列，接下来对删去的项分类讨论，一共有四种情况．若删去a1或a4，剩下的三项既等差又等比，则d=0，矛盾；所以只能删去a2或a3，接下来再分类讨论．

师：好！你说我来板书．

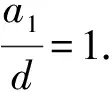
师：非常好！思路清晰，语言简洁，结论也正确，但美中不足的是还不够严谨．

师：对！这是最容易扣分的地方．第(2)题如何处理，也请一个同学来分享一下思路．

生2：项数大于等于6时，无论删去该数列哪一项，剩下的项中总有三项是原等差数列中的连续三项，若成等比，则d=0，矛盾．下面考虑项数等于5的情形：

对于数列a1,a2,a3，a4,a5，若删去a1,a2,a4,a5中的任意一项，得到的数列中总有三项既等差又等比，则d=0，矛盾.当删去a3时，由a1,a2,a4,a5成等比数列，得a1(a1+4d)=(a1+d)(a1+3d)，解得d=0，矛盾. 综上，n=4．

师：非常好！从两位同学分享的解题过程来看，这道题的关键是分类讨论，同时要注意“a，b，c等比”与“b2=ac”之间并不等价．另外，既等差又等比的数列是常数列，知道这个结论，对解这道题也非常有益．

片段2

师：请大家先看一道小题：

等差数列a,b,c，公差为d．若数列a,b,c也是等比数列，则d=．

众生：0．

师：既等差又等比的数列是常数列，这个小结论看似不起眼，但在2008年江苏高考第19题中却发挥了大作用，大家有没有兴趣来做一番探究？ 教师用PPT出示探究1：

探究1如果一个等差数列项数为4，且公差d≠0，若将此数列删去某一项，得到的数列(按原来的顺序)能不能是等比数列？

在学生思考1分钟后，教师开始提问．

生1：假设存在等差数列为a1,a2,a3,a4，且d≠0，下面对删去的项进行分类讨论：

若删去a1，则a2,a3,a4是等比数列，故a1(a1+3d)=(a1+2d)2，公差d=0，与题设矛盾；同理，若删去a4，公差d=0，与题设矛盾；故只能删去a2或a3．

此时，数列为-4d，-3d，-2d，-d，满足要求；

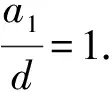
此时，数列为d，2d，3d，4d，满足要求．

师：大家能提出类似于探究1的问题吗？可以展开讨论.

生2：还可以探究等差数列的项数为5的情况．

师：说说你的解题过程．

生2：假设存在数列a1,a2,a3,a4,a5满足条件，若删去a1,a2,a4,a5中的任意一项，得到的数列中总有三项既等差又等比，根据结论得d=0，与条件矛盾．若删去a3，此时a1,a2,a4,a5是等比数列，则a1·a5=a2·a4，即a1(a1+4d)=(a1+d)(a1+3d)，解得d=0，与条件矛盾，所以不可能是等比数列．

师：还能提出类似的问题吗？

生3：类似的问题多了，比如项数等于6，等于7，等等．

师：是吗？

生3：哦，不对不对．项数超过5时，若删去某一项后得到的数列(按原来的顺序)是等比数列，则这个数列一定是常数列，所以对项数再进行探究没有意义．

师：能根据这个发现编制一道填空题吗？请大家思考．

生4：若一个等差数列项数为n(n≥5),如果删去某一项后得到的数列(按原来的顺序)是等比数列，则公差d=．(答案：0)

生5：若一个等差数列项数为n(n≥4)，且公差d≠0，若将此数列删去某一项得到的数列(按原来的顺序)是等比数列，则n的所有可能值为．(答案：4)

师：非常好！生5编的填空题其实就是高考题．(教师投影高考题，学生惊叹不已)我们的探究结束了吗？能不能再提出一些新的思考？

生6：把等差数列换成等比数列．

师：好主意！等差横向类比等比，这是数列问题惯用的探究方式之一，大家不妨先从项数为4，且公比q≠1的等比数列入手．

教师巡视后投影学生的探究过程：

假设存在等比数列a1,a2,a3,a4，且q≠1. 若删去a1，则a2,a3,a4是等差数列，故a1q+a1q3=2a1q2，公比q=1，与题设矛盾；同理，若删去a4，公比q=1，与题设矛盾；故只能删去a2或a3．

师：改变项数，有没有类似等差数列的发现．

生7：项数n≥5时，若将此等比数列删去某一项后得到的数列(按原来的顺序)是等差数列，则公比q=1．

生8：若一个等比数列项数为n(n≥4)，且公比q≠1，若将此数列删去某一项得到的数列(按原来的顺序)是等差数列，则n的所有可能值为．(答案：4)

………

评注片段2中，整个教学过程总耗时近30分钟.教师从一个学生熟知的小结论入手，起到先行组织者的作用；用“这个结论看似不起眼，但在高考题中能发挥大作用”这句话去吊足学生的胃口，激发学生的探究欲望，真是“小技巧，大智慧”．探究1是教师预先准备好的，它既承接了前面的小结论：等差又等比的数列是常数列，相当于对小结论进行了一个变式运用；又降低了题目的难度，符合高一学生的学情，实际上高考原题的表述，不少高三学生也感到抽象、有难度，高一学生更是如此；更为重要的是，探究1还是一个激活学生问题意识的“源代码”，引发了学生对项数从4项到5项，再到n(n≥5)项的推广，对数列类型由等差到等比的横向类比．在学生这一连串的探究发现、自然生成之间，教师如同双口相声中的捧哏，穿针引线、递火点鞭，适时、适度的激发学生的思维，把精彩留给学生，学生收获的不仅是知识，伴随着知识的生成，学生的问题意识、数学思维、数学能力及数学素养都得到了提升．同一道题目，不同的处理方法，前者耗时近15分钟，后者耗时近30分钟，也许，把片段2中学生提出的问题转化成题目，片段1中的学生也许都能解决，但正如爱因斯坦所说的：“提出一个问题往往比解决一个问题更为重要，……”，从这个角度来说，这多花的将近一倍的时间非常值！

3 几点思考

3.1 激活学生的问题意识，需要创设开放式的教学情境

开放式教学渊源于科恩(R．C．Cohn)1969年创建的以题目为中心的“课堂讨论模型”和“开放课堂模型”——人本主义的教学理论模型；同时，还渊源于斯皮罗(Spiro)1992年创建的“随机通达教学”和“情景性教学”——建构主义的教学模式．这些教学理论模型强调：学习是学习者主动建构的内部心理表征过程，教师的角色是思想的“催化剂”与“助产士”．开放式教学需要创设开放式的教学情境，开放式的教学情境包括开放式的现实情境、开放式的数学情境以及开放式的科学情境，但不管是什么类型的教学情境，都应该突出以提出问题、发现问题和解决问题为中心，注重学生自主探索与师生合作交流，重视数学联系与知识建构，充分关注学生数学学习中的情感和态度[1]．创设开放式的教学情境，就是给学生的问题意识得到激活创造了最为合适的温度和环境．

3.2 激活学生的问题意识，需要保护学生的好奇心

当前，高中阶段单一的考试评价制度依然支配着教与学的价值取向，分数成为素质教育难以逾越的屏障，“快节奏、大容量”式的教学(不止是数学课堂)成为高效课堂的流行标签，日臻成熟的“刷题”流水线在夯实数学基础知识，提高解题技能的同时，也抹平了学生的棱角，扼杀了学生的好奇心和想象力．然而，好奇心是想象力的源泉，没有好奇心，就没有想象力．所以，日常教学中要改变过分依赖接受记忆、机械模仿等进行数学学习的方式；要给学生提供探究发现的机会，鼓励学生

质疑提问，给学生提供表达自己的见解、思路和提出问题的机会；要善于发现学生的闪光点，及时给予肯定、鼓励和表扬；在解题教学中，为激发学生的兴趣和好奇心，激活学生的问题意识，对合适的内容要尝试拆解和重组，以便于进行探究性学习，而不能仅仅停留在就题论题的层面上．创造力需要知识，但不仅仅是知识．“我没有特殊的天赋，我只是极度的好奇”、“想象力比知识更重要”，爱因斯坦的两句话无不发人深思．保护学生的好奇心，就是呵护学生问题意识萌芽和茁壮成长的种子．

3．3 激活学生的问题意识，需要提升教师的问题意识

随着新课改的深入推进，“问题导向”的课堂教学模式受到一线教师的广泛关注和普遍欢迎.“问题”是“导向”的媒介，好的问题不仅能精准制导，而且能提高学生的思维质量、激活学生的问题意识．好问题的来源不外乎两类：一类是教材、教辅等资料上已有的，另一类是集师生智慧而生成的．现代教学观下，学生的主体性需要得到充分关切，但班级授课制下教师依然是提出问题的主体．课堂观察表明，因教师自身生成问题的意识淡薄而错过了发问的最佳时机，因教师自身生成问题的能力不足而出现了不是问题的伪问题或者是缺少思维含量的低端问题，因教师垄断发问的权限而导致学生的问题意识得不到激活和呵护，如此种种，学生一直扮演着被动解决问题的角色，学生的智力活动呈现出单一的、机械的特征．“给学生一杯水，教师要有一桶水，而且是活水”，教师提升自身的问题意识，就是给激活学生的问题意识引进的源头活水．